Authors: Mirror Tang , Shixiang Tang , Shawn Chong ,Yunbo Yang
Introduction
Ethereum is a blockchain-based open platform that allows developers to build and deploy smart contracts. Smart contracts are programmable codes on Ethereum that enable the creation of various applications. With the development of Ethereum, certain issues and challenges have emerged, including privacy concerns in applications. Defi applications involve a large amount of address information and user funds. Protecting the privacy of transactions is crucial for users in certain application scenarios. By utilizing privacy-preserving technologies, transaction details can be made visible only to involved parties and not to the public. Through the use of ZK-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge), we can implement transformations on existing applications on Ethereum. This includes adding features such as private transfers, private transactions, private orders, and private voting to existing projects on Ethereum, as well as optimizing computations and addressing MEV (Maximal Extractable Value) challenges in Ethereum application-layer projects.
Through this research, our aim is to promote privacy in the Ethereum application layer and address issues related to privacy transformation, computational optimization (such as Rollup), and MEV resistance on Ethereum.
Existing Issues
-
Competitor Analysis: Smart contracts without privacy features are susceptible to competitor analysis and monitoring. Competitors can gain sensitive information about business operations and strategies by observing and analyzing transaction patterns and data of the contract, thereby weakening competitive advantages.
-
Transaction Traceability: In the absence of privacy features, contract transactions are traceable, and the participants and contents of the transactions can be tracked and identified. This exposes transaction intentions and participants for certain transactions, such as anonymous voting or sensitive transactions.
-
Data Security: Data in smart contracts has become a primary target for attackers. Contracts without privacy features are at risk of data leakage, tampering, or malicious attacks. Attackers often exploit and manipulate contract data through analysis to carry out malicious activities, causing harm to users and contracts.
Technical Barriers
EVM Smart Contract Multithreading: Currently, direct implementation of multithreading is not possible in Ethereum smart contracts. Ethereum adopts an account-based execution model, where each transaction is executed sequentially in a single thread. This is because Ethereum’s consensus mechanism requires sequential verification and execution of transactions to ensure consensus among all nodes. Smart contracts in Ethereum face performance bottlenecks when dealing with large-scale data. To run a significant number of smart contracts containing zero-knowledge proofs on-chain, optimizations such as asynchronous calls, event-driven programming, and delegation splitting need to be implemented to achieve concurrent execution.
Auditable Zero-Knowledge (ZK): Auditable ZK refers to the ability of verifiers to provide received zero-knowledge proofs to third parties (usually the public) for verifying their validity without going through the entire proof process again. This means that third parties can verify the correctness of the proof without knowing the specific details of the statement. Auditable ZK requires more computation and storage operations compared to general ZK implementations, especially in the verification phase. This may have an impact on the performance and resource consumption of smart contracts, placing higher demands on the performance optimization of Solidity and corresponding ZK circuits.
Proof System Scalability: Existing proof systems suffer from scalability issues, making it difficult to support large-scale circuits, such as proving LLM circuits. Current potential scalability solutions include recursive proofs and distributed proofs, which have the potential to enhance the scalability of proof systems and provide solutions for proving large-scale circuits.
Proof System Security Risks: Some proof systems, such as Groth16 and Marlin, rely on a trusted setup (also known as toxic waste) that is privately generated. Once made public, the security of the entire proof system cannot be guaranteed.
Currently Used zk-SNARKs Schemes
Groth16 (Used by Zcash currently)
In the case where the adversary is restricted to only linear/affine operations, Groth constructed a LIP with a communication cost of only 3 elements based on QAP. Based on this LIP, it constructed a zk-SNARK with a communication cost of 3 group elements and a verifier computational cost of only 4 pairing operations (known as Groth16).
Advantages: Small proof size, currently the fastest verification speed.
Disadvantages: Trusted setup bound to the circuit, meaning that a new trusted setup is required for generating proofs for a different circuit, and the trusted setup cannot be dynamically updated.
Marlin
To address the inability of zk-SNARKs schemes to achieve global updates, Groth et al. based on QAP, proposed a zk-SNARK with a global and updatable Common Reference String (updatable universal CRS), denoted as GKMMM18.Building on this, Maller et presented Sonic scheme that utilized the permutation argument, grand-product argument, and other techniques to achieve a globally updatable CRS with a size of O(|C|), concise NIZKAoK without additional preprocessing, under the algebraic group model.
Marlin is a performance-improved scheme of Sonic (as is Plonk), primarily optimizing the SRS preprocessing and polynomial commitment, thereby reducing the proof size and verification time of the proof system."
Advantages: Support for globally updatable trusted setup, achieving succinct verification in an amortized sense.
Disadvantages: High complexity in the proof process, less succinct proof size compared to Groth16.
Plonk
Plonk is also an optimization of the Sonic scheme, introducing a different circuit representation called Plonkish, which is different from R1CS (Rank-1 Constraint System) and allows for more scalability, such as lookup operations. Plonk optimizes permutation arguments through “Evaluation on subgroup rather than coefficient of monomials” and leverages Lagrange basis polynomials.
Advantages: Support for globally updatable trusted setup, fully succinct verification, and a more scalable circuit representation in Plonkish.
Disadvantages: Marlin may perform better in cases with frequent large addition fan-in; less succinct proof size compared to Groth16.
HALO2
To reduce proving complexity and the burden on the Prover, researchers introduced recursive proofs and proposed the Halo proof system (as introduced by Vitalik’blog). The Halo proof system adopts the Polynomial IOP (Interactive Oracle Proof) technique from Sonic, describes a Recursive Proof Composition algorithm, and replaces the Polynomial Commitment Scheme in the algorithm with the Inner Product argument technique from Bulletproofs, eliminating the reliance on a Trusted Setup.
Halo2 is a further optimization of Halo, mainly in the direction of Polynomial IOP. In recent years, researchers have discovered more efficient Polynomial IOP schemes than those used in Sonic, such as Marlin and Plonk. Among them, Plonk was chosen due to its support for more flexible circuit designs.
Advantages: No need for a trusted setup; introduces recursive proofs to optimize proof speed.
Disadvantages: Less succinct proof size.
Circom + Snarkjs
Circom + Snarkjs is a major tool chain to build the zkSNARK proving system. Snarkjs is a JavaScript library for generating zk-SNARK proofs. This library includes all tools required to build a zkSNARK proof. To prove the validity of a given witness, an arithmetic circuit is first generated by Circom, then a proof is generated by Snarkjs. For the usage about this tool chain, we refer the reader to the guidance.
Advantages: This toolchain inherits the advantages of zkSNARKs such as Groth16, namely having smaller proof sizes and faster verification times. In order to reduce overall costs, The computationally expensive operations (FFT and MSM) at the prover side can be done off-chain. If Groth16 is used for proving, the proof size on-chain consists of only three group elements, and the verifier can validate proof in a very short time, which leads to lower gas fee. In addition, this tool chain can handle large-scale computing, and the proof size as well as verification time is independent of the size of the computation task.
Disadvantages:This language is not particularly ergonomic, making developers keenly aware that they are writing circuits.
Performance comparison
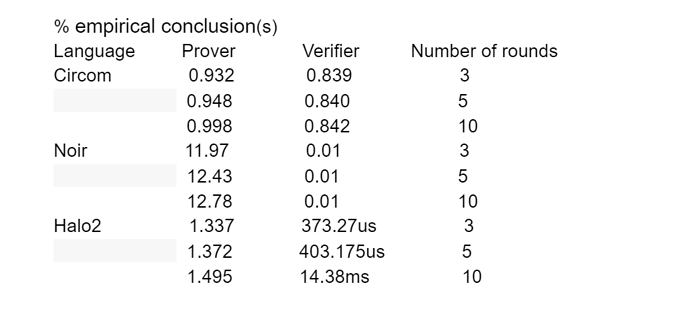
We use different programming languages (Circom, Noir, Halo2) to write the same circuit, and then test the proving and verifier time with different numbers of rounds. We run all experiments on the Intel Core i5 processor with 16GB RAM and MacOS 10.15.7. The experimental codes are shown in [link] .
The above table is the experimental results. It shows that the circuit written in Circom outperforms in terms of the prover time, with only around 1s for 10 rounds, and Halo2 outperforms in terms of the verifier time when the circuit size is small.
Both the circuit written in Circom and Noir relies on KZG commitment. Therefore, the overall verifier time of Circom and Noir is independent of the circuit size (number of rounds in the table). Meanwhile, Halo2 relies on the commitment scheme called inner product argument (IPA). The verifier time of IPA is logarithmic to the circuit size. With the increment of circuit size, the verification time will increase gently.
Generally speaking, circuit written in Circom enjoys the best prover time and verification time.
Enclave: interactive shielding
In terms of privacy protection, pure zk proving system can not construct a complete solution. For example, when considering the privacy of transaction information, we can use ZK technology to construct a dark pool. Orders within this dark pool are in a shielded state, which means they are obfuscated, and their contents cannot be discerned from the on-chain data by anyone. This condition is referred to as “fragmentation in shielded state.” However, when users need to maintain state variables, i.e., initiate transactions, they have to gain knowledge of these shielded pieces of information. So, how do we ascertain shielded information while ensuring its security? This is where enclaves come into play. An enclave is an off-chain secure storage area for confidential computations and data storage. How do we ensure the security of enclaves? For the shielding property in the short term, one may use secure hardware modules. In the long term, one should have systems in place for transitioning to trust-minimized Multi-Party Computation (MPC) networks.
With the introduction of enclaves, we will be able to implement interactive shielding. Namely, users can interact with fragmented shielded information while ensuring securiry. Implementing interactive shielding opens up unlimited possibilities while maintaining privacy.
The ability to have shielded state interact opens up a rich design space that’s largely unexplored. There’s an abundance of low hanging fruit:
- Gamers can explore labryinths with hidden treasures from previous civilizations, raise fortresses that feign strength with facades of banners, or enter into bountiful trade agreements with underground merchants.
- Traders can fill orders through different dark pool variants, insure proprietary trading strategies through RFQ pools with bespoke triggers, or assume leveraged positions without risk of being stop hunted.
- Creators can generate pre-release content with distributed production studios, maintain exclusive feeds for core influencers, or spin up special purpose DAOs with internal proposals for competitive environments.
Currently available ZK enclaves:
How to integrate with Solidity?
For the Groth16 and Marlin proof systems, there are already high-level circuit languages and compilers that provide support for solidity, such as Circom for Groth16 and Plonk, and zokrate for Groth16 and marlin proof systems.
For the halo2 proof system, Chiquito is the DSL of HALO2(Provided by Dr. CathieSo from the PSE team of the Ethereum Foundation):
Scenario demonstration of ZK-SNARKs integration using Solidity
Privacy Enhencement
Assuming we need to hide the price of a limit order from the chain and the order is represented as O=(t,s) , where t:= (\phi, \chi, d) , s:= (p, v, α)
\phi: side of the order, 0 when it’s a bid, 1 when it’s an ask
\chi: token address for the target project
d: denomination, either the token address of USDC or ETH. Set 0x0 represent USDC and 0x1 represent ETH.
p: price, denominated in d
v: volume, the number of tokens to trade
\alpha: access key, a random element in bn128’s prime field , which mainly used as a blinding factor to prevent brute force attacks
The information we want to hide is the price, but in order to generate proof, we must expose the value related to the price, which is the balance b required for this order. Specifically, if it’s a bid order, the bidder need to pay the required amount of denomination token for the order; If it is a ask order, the seller needs to pay the target token they want to sell. The balance b is a pair with the first element specifying an amount of the target project’s token and the second element specifying an amount of the denomination token.
In general, we use poseidon hash to mask out the price and volume of the order and only display the balance required for this order. We use zksnark to prove that the balance is indeed consistent with the price required for the order.
Here is the example circom code:
pragma circom 2.1.6;
include "circomlib/poseidon.circom";
// include "https://github.com/0xPARC/circom-secp256k1/blob/master/circuits/bigint.circom";
template back() {
// 1. load input
signal input phi; // order type, 0 when it is a bid order, otherwise 1
signal input x; // target token address
signal input d; // domination
signal input p; // price
signal input v; // volumn
signal input alpha; // access key
// 2. define output and temporary signal
signal output O_bar[4];
signal output b[2];
signal temp;
// 3. construct shielded order O_bar
// check phi
phi * (phi - 1) === 0;
O_bar[0] <== phi;
O_bar[1] <== x;
O_bar[2] <== d;
component hasher = Poseidon(3);
hasher.inputs[0] <== p;
hasher.inputs[1] <== v;
hasher.inputs[2] <== alpha;
O_bar[3] <== hasher.out;
// 4. compute b
// if it's a bid, b[0] = 0, b[1] = p * v
// else, b[0] = v, b[1] = 0
b[0] <== v * phi;
temp <== p * v;
b[1] <== (1 - phi) * temp;
}
component main{public [phi, x, d]} = back();
/* INPUT = {
"phi": "1",
"x": "0x0",
"d": "0x1",
"p": "1000",
"v": "2",
"alpha": "912"
} */
Prover can use the above circuit to generate proof for specific orders using the Circom+Snarkjs toolchain. The Snarkjs tool can export Verifier.sol, with the following content [I am using the plonk proof system]. Run command:
snarkjs zkey export solidityverifier final.zkey verifier.sol
then we get the verifier.sol
And then, the project developer can use the verifier.sol to construct their project with solidity. The following code is just for demonstration.
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
import "./Verifier.sol";
contract PrivacyPreservingContract {
Verifier public verifier;
struct ShieldedOrder {
uint phi; // order type
uint x; // target token address
uint d; // domination
uint h; // hash
}
ShieldedOrder[] public orders;
constructor(address _verifier) {
verifier = Verifier(_verifier);
}
function shieldOrder(
uint[2] calldata a,
uint[2][2] calldata b,
uint[2] calldata c,
uint[4] calldata input
) public {
// verify the zk-SNARK proof
require(verifier.verifyTx(a, b, c, input), "Invalid proof");
// create the shield order
ShieldedOrder memory newOrder = ShieldedOrder({
phi: input[0],
x: input[1],
d: input[2],
h: input[3],
});
// Store new orders in status variables
orders.push(newOrder);
}
// your project logic
}
The last thing I need to emphasize that privacy enhancement has actually brought MEV resistance to this project. So I will no longer do anti MEV demonstrations.
Computational Optimization
Assuming we want to execute the heavy AMM logic off-chain, we only need to perform computational verification operations on the chain.
The following is a simple AMM logic circuit (as an example only, the calculation logic of the actual protocol is much more complex)
template AMM() {
signal input reserveA;
signal input reserveB;
signal input swapAmountA;
signal output receivedAmountB;
signal output newReserveA;
signal output newReserveB;
// x * y = k
// newReserveA = reserveA + swapAmountA
// newReserveA * newReserveB = reserveA * reserveB
// newReserveB
newReserveA <== reserveA + swapAmountA;
newReserveB <== (reserveA * reserveB) / newReserveA;
// compute the amount of tokenB
receivedAmountB <== reserveB - newReserveB;
// more computation operations...
}
component main = AMM();
Similarly, it is necessary to use the circom+snarkjs toolchain to generate proof and export it to verifier.sol.
Finally, AMM project developers can develop their logic code with verifier.sol in solidity. The example solidity code for the on chain check contract is as follows:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
import "./Verifier.sol";
contract AMMWithSnarks {
Verifier public verifier;
constructor(address _verifier) {
verifier = Verifier(_verifier);
}
function swap(
uint[2] memory a,
uint[2][2] memory b,
uint[2] memory c,
uint[2] memory input,
uint256 amountA
) public returns (uint256) {
// Verification of zk-SNARKs proofs
require(verifier.verifyTx(a, b, c, input), "Invalid proof");
// The actual exchange logic is omitted, as the verification is done through zk-SNARKs
// Return the amount of tokens obtained after the exchange, which requires calculation in the actual implementation
return amountA * 2; // Here is just an example of the return value
}
// other function,such as addLiquidity, removeLiquidity etc.
}
Anti-MEV attacks
After privacy modification of protocol contracts, MEV attacks often fail to be achieved. Please refer to examples of privacy modification.
Conclusions
From the example above, we can see that integrating ZK-SNARKs technology into Solidity can effectively address issues of privacy, computational optimization, and resistance to MEV (Maximum Extractable Value) in Ethereum applications. ZK-SNARKs offer privacy features, making it possible to implement private transfers, private transactions, private orders, and private voting within existing Ethereum projects. At the same time, ZK-SNARKs can optimize computational processes and address challenges related to MEV resistance in application-layer projects on Ethereum. By leveraging ZK-SNARKs technology, developers can enhance the privacy, performance, and security of their applications. This reaffirms the feasibility of writing ZK applications in Solidity on Ethereum and indicates that it is a trend for future development. This will bring improved privacy protection, computational optimization, and MEV resistance capabilities to the Ethereum ecosystem, propelling further development and innovation in Ethereum applications.
Possible Improvements and Future Work
Establishing a Public ZK Verification Layer on the Ethereum Blockchain
This can provide various benefits such as privacy protection, scalability, flexibility, and extensibility. This can help drive the adoption of ZK technology in the Ethereum ecosystem and provide users and developers with more secure, efficient, and flexible verification solutions.
ZK Performance Optimization in Solidity
Considering methods such as batching techniques, optimizing computation and communication, parallel computing, caching and precomputation, and optimizing the verification process to improve the performance of ZK calls in Solidity. Enhancing the computational efficiency of ZK proofs, reducing communication overhead, and improving the overall performance of the ZK system.
Establishing Reusable Solidity ZK Components
This contributes to code maintainability and reusability, promotes collaboration and sharing, improves code scalability, and provides better code quality and security. These components can help developers efficiently develop Solidity applications and also contribute to the growth and development of the entire Solidity community