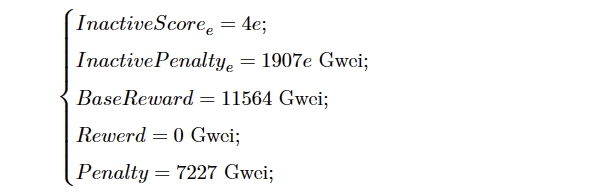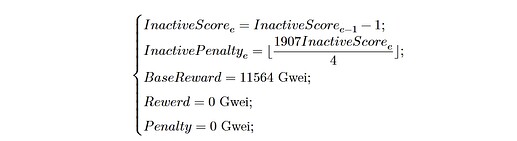The Safety Attack against PoS

[mart1i1n]

Description

ETH consensus uses a pseudorandom number RANDAO to choose the attester and proposer roles in each epoch. However, this random number choice can cause a safety attack against Ethereum. This attack can finalize two conflict chains without violating the 1/3-slashable assumption. The basic idea of the attack is as follows:

Attack scenario

Assumption

• Assume that the adversary has the ability for a short-time network partition. This is possible because the Ethereum consensus is in safety under the asynchronous model.

• Also we assume that 33% of total validators are adversarial.

Attack with Network Partition

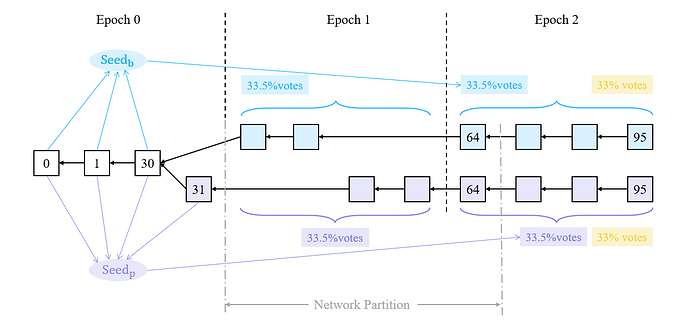
First, we assume that the network partition lasts for 1 epoch. Notice that the assumption is strong, but this attack is easy to follow. The attack starts at an epoch when the last block proposer is adversarial. We denote this epoch as epoch 0 for simplicity. Notice that epoch 0 is not actual epoch 0 in reality.

1. During epoch 0, the adversary withholds all the attestations and the last block of epoch 0 (block 31).
2. At the beginning of epoch 1, the adversary split the honest validators into two parts, blue and purple. Each part has 33.5% of total validators. Then the adversary releases block 31 to purple but not to blue in epoch 1. So during epoch 1, the blue validators build the blue blocks upon block 30. And the purple validators build the purple blocks upon block 31.
3. The network gets well at the end of slot 64 (the first slot of epoch 2).

Analysis
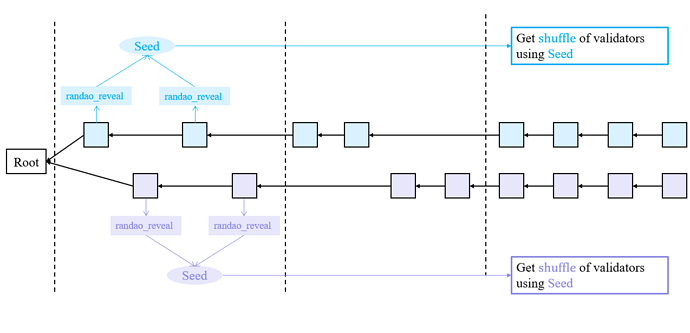
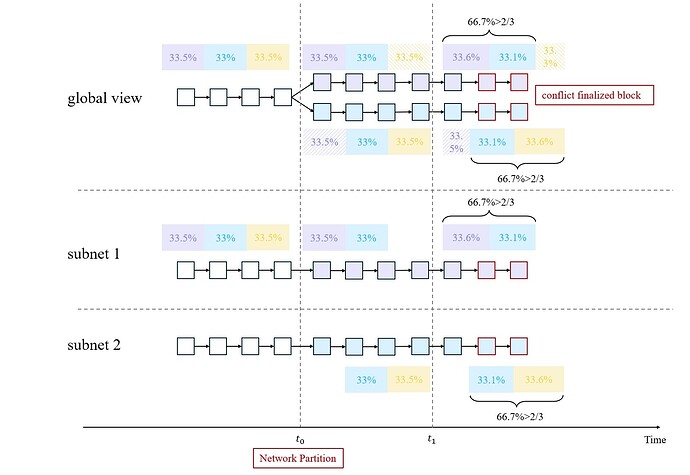
At the beginning of epoch 2, the blue validators use the randao_reveal of block 0, block 1, …, block 30 and get seed_{\text{b}}. The purple validators use the randao_reveak of block 0, block 1, …, block 30, block 31 and get seed_{\text{p}}. These two seeds are different. So the blue validators and purple validators get different shuffles of validator indices. This leads that the blue votes are invalid to purple validators and also the purple votes are invalid to blue validators. So at the end of slot 64, in the view of purple validators, the purple chain gains more weight than the blue chain. The purple validators continue to build blocks on the purple chain. So does blue validators. Starting from epoch 2, the validators build two chains. And the messages of one part are invalid to another part. So the adversary can join in two parts. The adversary uses seed_{\text{b}} to cast vote_{\text{b}} on the blue chain and uses seed_{\text{p}} to cast vote_{\text{p}} on the purple chain. This double-vote action does not violate slashing condition 1 because vote_{\text{b}} and vote_{\text{p}} cannot both be valid for all validators. So both chains gain 66.5% votes and become finalized.

Attack without Network Partition

This attack use the delay of justification (See Voting Delay Attack) to replace the network partition. But we assume that the adversary has an new ability.

• The adversary can delay some honest attestations for some slots. This is possible because the Ethereum consensus is in safety under the asynchronous model.

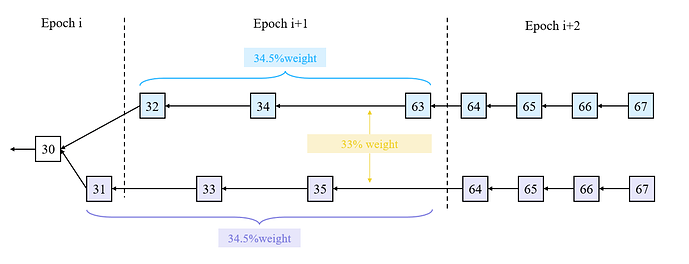
We also assume that the last block proposer of epoch 0 is adversarial. In addition, we assume that block 34 is controlled by adversary. We denote \beta=\frac{1}{3}\times\frac{1}{32}\times total\_stake. The detail of attack is as follows:

1. During epoch 0, the adversary withhold all the attestations and block 31. The justification of epoch 0 is delayed to epoch 1. The block 31 contains enough attestations to justify epoch 0. The honest attestations in slot 31 is delayed by the adversary for 3 slots. So block 34 can contain these attestations to justify epoch 0.
2. In slot 32, the block 32 builds upon block 30 (denote as blue chain). The adversary withholds the attestations in slot 32. So the blue chain gains 2\beta weight.
3. In slot 33, the block 31 is released. Because of the justification of epoch 0, block 33 build upon block 31 (denote as purple chain). The adversary also withhold the attestations in slot 33, so the purple chain gains 4\beta weight.
4. In slot 34, the block 34 is proposed by the adversary upon blue chain. So blue chain also justify epoch 0. At that time, blue chain and purple chain both gain 4\beta weight.
5. From slot 35 to slot 63, the adversary release some withheld attestations at proper time to maintain the balance of two chains. The adversary monitor the weight of two chains in real time, and release the attestations to some validator first to change its choice of heavies tree.
6. At slot 64 (the beginning of epoch 2), the adversary release some attestations to split the honest validators into two parts (blue and purple).
   
   

The analysis is same as the previous one.

[fradamt]

@mart1i1n

These two seeds are different. So the blue validators and purple validators get different shuffles of validator indices. This leads that the blue votes are invalid to purple validators and also the purple votes are invalid to blue validators

Validators which see the blue chain as canonical at the end of the network partition can still process the other chain and the votes for it, and they can switch to it, and viceversa.

@mart1i1n

The adversary uses seed_{\text{b}} seedbseed_{\text{b}} to cast vote_{\text{b}} votebvote_{\text{b}} on the blue chain and uses seed_{\text{p}} seedpseed_{\text{p}} to cast vote_{\text{p}} votepvote_{\text{p}} on the purple chain. This double-vote action does not violate slashing condition 1 because vote_{\text{b}} votebvote_{\text{b}} and vote_{\text{p}} votepvote_{\text{p}} cannot both be valid for all validators. So both chains gain 66.5% votes and become finalized.

For a pair of attestations to be slashable in a certain chain, it doesn’t have to be the case that they are attestations which can be processed on that chain. It only has to be the case that they violate the FFG slashing rules and that they pass this minimal validity check (other than formal things about the aggregate attestation, this is just checking the signatures):

def is_valid_indexed_attestation(state: BeaconState, indexed_attestation: IndexedAttestation) -> bool:
    """
    Check if ``indexed_attestation`` is not empty, has sorted and unique indices and has a valid aggregate signature.
    """
    # Verify indices are sorted and unique
    indices = indexed_attestation.attesting_indices
    if len(indices) == 0 or not indices == sorted(set(indices)):
        return False
    # Verify aggregate signature
    pubkeys = [state.validators[i].pubkey for i in indices]
    domain = get_domain(state, DOMAIN_BEACON_ATTESTER, indexed_attestation.data.target.epoch)
    signing_root = compute_signing_root(indexed_attestation.data, domain)
    return bls.FastAggregateVerify(pubkeys, signing_root, indexed_attestation.signature)

Here is the the full attester slashing function

[mart1i1n]

Overview

We have found a safety attack that can construct two conflicting finalized blocks without violating 1/3-slashable. The attack exploits Ethereum’s leaking mechanism, which gradually reduces the stake of non-voting nodes when the system becomes inactive, causing the proportion of stake held by voting nodes to increase gradually beyond 2/3. With a 33% assumed proportion of Byzantine nodes, the network requires approximately 2.5 days to execute this attack. The basic attack strategy is illustrated in the following diagram:

Assuming that the current stake proportion of malicious nodes in the system is 33% (represented in blue). At time t_0, the network experiences a split, causing honest nodes to be divided into two parts (purple and yellow), communicating in subnet 1 and subnet 2, respectively. In subnet 1, purple nodes communicate, while yellow nodes communicate in subnet 2. Byzantine nodes can communicate simultaneously in both subnets (asynchronous network assumption). For honest nodes in subnet 1, they can see messages from purple and blue nodes but cannot observe messages from yellow nodes. The same applies to honest nodes in subnet 2.

• From time t_0 to t_1, the stake proportion of nodes in each subnet is 66.5%, which is below 2/3. So the system is inactive. In subnet 1, the stake proportion of yellow nodes gradually decreases due to their lack of voting. In subnet 2, the proportion of purple nodes gradually decreases.
• At time t_1, the proportion of yellow nodes in subnet 1 decreases to 33.3%, and the stake proportion of purple nodes, along with blue nodes, exceeds 2/3. The system in subnet 1 begins to justify and finalize a new checkpoint in subnet 1. The same process occurs in subnet 2.
• After t_1, two finalized chains will emerge in the global network.

Value of t_1

To calculate t_1, we need to review the reward and penalty calculation scheme in Ethereum.

leaking reward and penalty

Leaking is Ethereum’s solution to address liveness issues arising from network splits. When the system goes four consecutive epochs without finalizing a new checkpoint, it enters an inactive state. In this state, the penalty for non-voting nodes increases with the duration of inactivity. According to reward, the specific reward and penalty calculation scheme in the inactive state is as follows:
Firstly, the system calculates the InactiveScore for a node v at epoch e.

Next, the system computes the InactivePenalty for a node v at epoch e.

Finally, the system determines the node normal Reward, and Penalty.

Actual Balance and Effect Balance

In Ethereum, all reward and penalty calculations, as well as the computation of voting weights, are based on Effective Balance (EB). However, the rewards and penalties actually impact the Actual Balance (AB). According to balance, the calculation rules for converting actual balance to effective balance are as follows:

Note: when a node continues to receive penalties, it will only affect the voting system once its actual balance decreases to 0.25 ETH less than the effective balance.

Calculation

According to beaconcha, there are 980,000 nodes with an average actual balance of 32.07 ETH per node in the current system. Assuming that the effective balance for each node is 32 ETH. Starting from t_0, the e-th epoch is as follows:

The total penalties incurred during these e epochs are 7227e + 1907 \times (1 + 2 + \cdots + e). To ensure a decrease in the effective balance, this value should be greater than 0.07 + 0.25 ETH. Therefore, we have 7227e+1907\times(1+2+\cdots+e)>0.32\times10^9. Hence, e should be greater than 575. With 225 epochs in a day, it would take only 2.5 days to construct two conflicting finalized blocks.

Conclusion

During the attack, no Byzantine node are slashed because of the network partition. Although these Byzantine nodes suffer from the slashing after the network is synchronous again, the stake ratio of Byzantine nodes slashed are less than 1/3.

[mart1i1n]

Besides, there is a strategy for Byzantine nodes to avoid be slashing.

If Byzantine nodes alternate their votes between two subnets, i.e., voting in subnet 1 in the first epoch and then voting in subnet 2 in the second epoch, they would not be slashed in this scenario. However, according to the calculation rules for rewards and penalties during the leaking period, malicious nodes would still incur penalties. For the e-th epoch starting from t_0, if the malicious node votes in this subnet, we have:

If the Byzantine nodes do not vote in this subnet, we have:

Obviously, the penalties incurred by the Byzantine nodes over two consecutive epochs are less than those incurred by honest nodes. When the actual balance of honest nodes decreases to 31.75 ETH, the actual balance of the Byzantine nodes remain greater than 31.75 ETH, and its effective balance stays at 32 ETH. Therefore, after 575 epochs, the ratio of stake between honest nodes and Byzantine nodes in the subnet exceeds 2/3.

In this scenario, to prevent the Byzantine nodes from being slashed, they do the following strategies:

• Byzantine nodes first vote consecutively in subnet 1 for multiple epochs to finalize a checkpoint in subnet 1.

• Then, Byzantine nodes vote consecutively in subnet 2 for next multiple epochs to finalize another checkpoint in subnet 2.

This achieves conflict finality without slashing any Byzantine nodes.

[kladkogex]

Vow! This needs to be studied in detail

[fradamt]

@mart1i1n

Although these Byzantine nodes suffer from the slashing after the network is synchronous again, the stake ratio of Byzantine nodes slashed are less than 1/3

That’s part of the security model. We cannot guarantee that 1/3 is slashed whenever there’s double finality. Instead, the guarantee we have is of this form: if two conflicting checkpoints are finalized within N epochs of their last common ancestor, we can slash at least 1/3 - D(N) of the stake, i.e., the economic security guarantees degrade over time. This is not just due to the existence of the inactivity leak, because we also have other ways for the validator set to change, i.e., activations and exit. The rate of change of the validator set (determined by the churn limit quotient) is bounded to ensure that D(N) does not increase too fast, i.e., that security degrades reasonably slowly over time (in the order of weeks)

@mart1i1n

If Byzantine nodes alternate their votes between two subnets, i.e., voting in subnet 1 in the first epoch and then voting in subnet 2 in the second epoch, they would not be slashed in this scenario.

Alternating votes between different chains does not prevent slashing.

[mart1i1n]

In the first attack I present, the ratio of stakes that violate the slashing condition is exactly less than 1/3, which strictly follows the assumptions in the Gasper paper. I acknowledge that almost all of them are slashed after the network reaches GST. However, this does not matter since the safety of Gasper is broken, and no assumption is violated.

In the second attack, no validator double votes or violates slashing condition 2. Unless the community takes other measures in the future, no validator in this attack will be slashed.

[fradamt]

@mart1i1n

In the first attack I present, the ratio of stakes that violate the slashing condition is exactly less than 1/3, which strictly follows the assumptions in the Gasper paper. I acknowledge that almost all of them are slashed after the network reaches GST. However, this does not matter since the safety of Gasper is broken, and no assumption is violated.

Papers often do their analysis with a static validator set. However, that’s just not our security model in practice. See weak subjectivity.

@mart1i1n

In the second attack, no validator double votes or violates slashing condition 2. Unless the community takes other measures in the future, no validator in this attack will be slashed.

You said that they vote on the top fork for multiple epochs, finalizing a checkpoint, and then switch to voting in the bottom fork, to finalize a conflicting checkpoint. This requires surround voting.