The Target Demand Paradox in the Blob Fee Market: An Analysis of EIP-4844 & EIP-7961

[Xiawpohr]

The Target Demand Paradox in the Blob Fee Market: An Analysis of EIP-4844 & EIP-7961

Thanks to Chih Cheng Liang for the feedbacks and discussions.

Introduction

EIP-4844 introduces a new transaction type to Ethereum that accepts ‘blobs’ of data, enhancing scalability for rollups by providing a more cost-effective data availability layer. As expected, rollup costs have dropped significantly due to the cheaper ‘blob’ resource. However, the overall price of blobs has remained exceptionally low for an extended period, raising concerns within the community about whether rollups are contributing enough to the mainnet.

The prevailing explanation for the persistently low blob prices is the cold-start problem, initially predicted by Davide Crapis. This theory suggests that it could take 1 to 1.5 years for blob demand to grow enough for prices to exceed 1 wei. However, in reality, prices remain low throughout a day, even as average blob consumption has approached the target value of 3.

In this research, I try to

• Find out how much blob demand needs to be created to bring the blob fee market into equilibrium
• Describe the target demand paradox
• Simulate where the blob fee is potentially headed after the Pectra fork

The blob fee mechanism

The blob fee structure is governed by a base fee update rule, which approximates the formula:

base_fee_per_blob_gas = MIN_BASE_FEE_PER_BLOB_GAS * e**(excess_blob_gas / BLOB_BASE_FEE_UPDATE_FRACTION)

In this equation, excess_blob_gas is the total “extra” amount of blob gas that the chain has consumed relative to the “targeted” number (TARGET_BLOB_GAS_PER_BLOCK per block). Like EIP-1559, it’s a self-correcting formula: as the excess goes higher, the base_fee_per_blob_gas increases exponentially, reducing usage and forcing the excess back down. Eventually base_fee_per_blob_gas goes toward a level at which rollups perceive it as a “fair” price.

The block-by-block behavior is roughly as follows. If block N consumes X blob gas, then in block N+1 excess_blob_gas increases by X - TARGET_BLOB_GAS_PER_BLOCK, and so the base_fee_per_blob_gas of block N+1 increases by a factor of e**((X - TARGET_BLOB_GAS_PER_BLOCK) / BLOB_BASE_FEE_UPDATE_FRACTION).

The parameter BLOB_BASE_FEE_UPDATE_FRACTION controls the maximum rate of change of the base fee per blob gas. It is chosen to target a maximum change rate of e**(TARGET_BLOB_GAS_PER_BLOCK / BLOB_BASE_FEE_UPDATE_FRACTION) ≈ 1.125 per block.

How blob demand effect the blob price

To gain initial intuitions into how blob demand impacts blob fees through the mechanism mentioned above, we conducted five simulations under different conditions to observe the changes in excess_blob_gas and base_fee_per_blob_gas.

The time range is 14,400 blocks (equivalent to 2 days). Each simulation is run 200 times, and the quartiles of excess_blob_gas are calculated for each block. The base_fee_per_blob_gas is then determined using the mean of excess_blob_gas.

The parameters are set as same as EIP-4844.

• TARGET_BLOB_PER_BLOCK: 3
• MAX_BLOBS_PER_BLOCK: 6
• MIN_BASE_FEE_PER_BLOB_GAS: 1 wei
• BLOB_BASE_FEE_UPDATE_FRACTION: 3338477

Scenario 1: The blob demand follows a Poisson distribution with lambda = 1

The mean and variance of blob consumption per block are both 1, which is below TARGET_BLOB_PER_BLOCK, indicating an oversupply situation. As expected, the results show that base_fee_per_blob_gas remains at the MIN_BASE_FEE_PER_BLOB_GAS value.

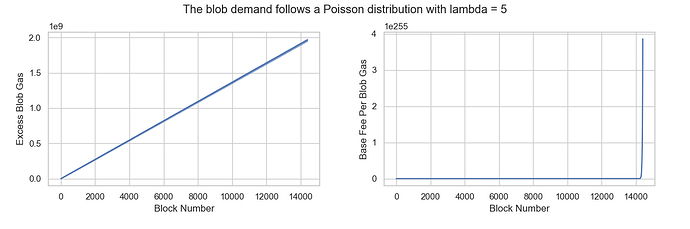
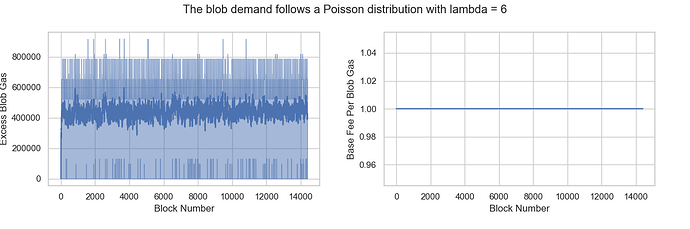
Scenario 2: The blob demand follows a Poisson distribution with lambda = 5

The mean and variance of blob consumption per block are both 5, which is more than TARGET_BLOB_PER_BLOCK, indicating higher-than-desired blob demand. If demand remains high, excess_blob_gas will continue to increase, causing base_fee_per_blob_gas to rise exponentially. As expected, the results confirm this trend.

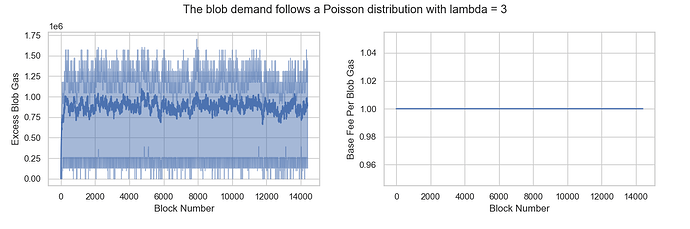
Scenario 3: The blob demand follows a Poisson distribution with lambda = 3

The mean blob consumption per block is 3, matching TARGET_BLOB_PER_BLOCK, representing a balanced state. In this scenario, base_fee_per_blob_gas is expected to remain stable without any upward or downward trend. The results confirm this, showing that base_fee_per_blob_gas stays at MIN_BASE_FEE_PER_BLOB_GAS, even though excess_blob_gas is higher than in Scenario 1.

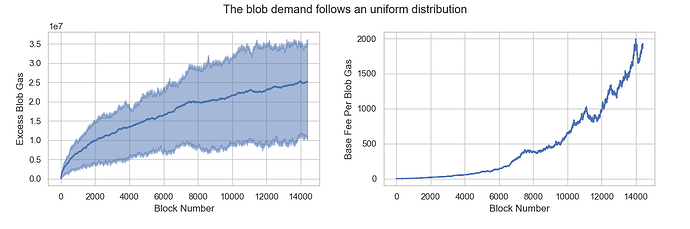
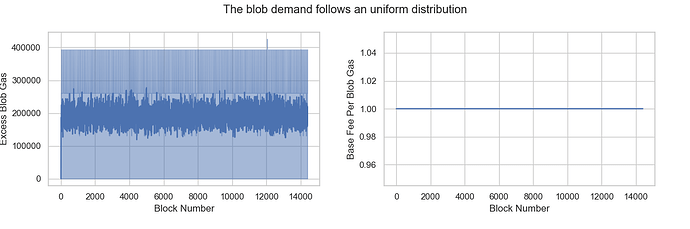
Scenario 4: The blob demand follows an uniform distribution

The mean blob consumption per block is 3, the same as in Scenario 3, but with a higher variance of 4.0, indicating greater volatility in blob usage. The results show that excess_blob_gas increases to a level where base_fee_per_blob_gas rises above MIN_BASE_FEE_PER_BLOB_GAS. Over time, both excess_blob_gas and base_fee_per_blob_gas tend to stabilize, reaching an equilibrium.

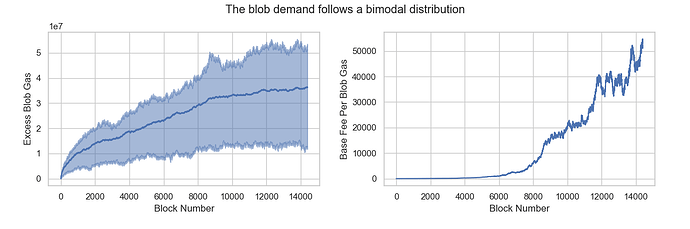
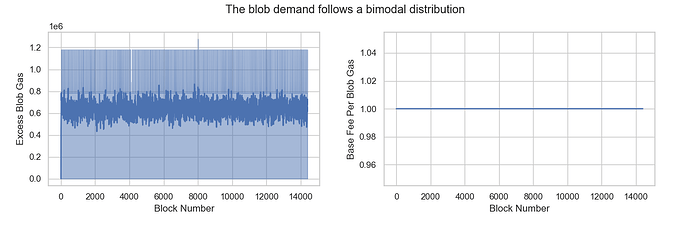
Scenario 5: The blob demand follows a bimodal distribution with mean = 3

What happens when blob demand becomes highly volatile? In Scenario 5, there is a 50% chance of consuming 0 blobs and a 50% chance of consuming 6 blobs. Despite this fluctuation, the mean of blob consumption remains 3, equal to TARGET_BLOB_PER_BLOCK, but with a higher variance of 9.0.
The results are similar to Scenario 4, where excess_blob_gas and base_fee_per_blob_gas tend to gradually stabilize over time. However, both values in Scenario 5 are higher than those observed in Scenario 4.

Insufficient demand, Effective demand, Excess demand

Based on the results above, we can categorize blob demand growth into three stages:

• Insufficient Demand: In this stage, excess_blob_gas doesn’t increase, and base_fee_per_blob_gas stays at MIN_BASE_FEE_PER_BLOB_GAS.
• Effective Demand: Both excess_blob_gas and base_fee_per_blob_gas gradually stabilize, reaching an equilibrium over time.
• Excess Demand: excess_blob_gas grows linearly, while base_fee_per_blob_gas rises exponentially.

Find the effective demand in the blob fee market

The next question explores how many consumed blobs per block would establish market equilibrium from scratch.

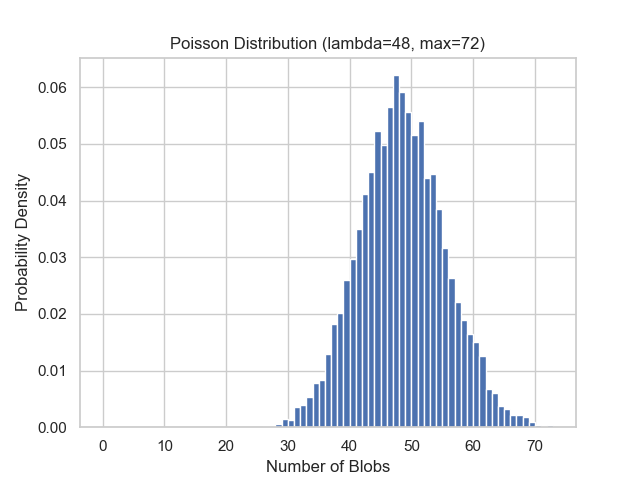
Under assumption that blob demand follows a Poisson distribution. We conducted simulations with means ranging from 3 to 4, using increments of 0.01.

The results indicate that effective demand falls between 3.13 and 3.20 blobs. When consumption drops below 3.13 blobs, demand becomes insufficient. Conversely, when consumption exceeds 3.20 blobs, demand becomes excess.

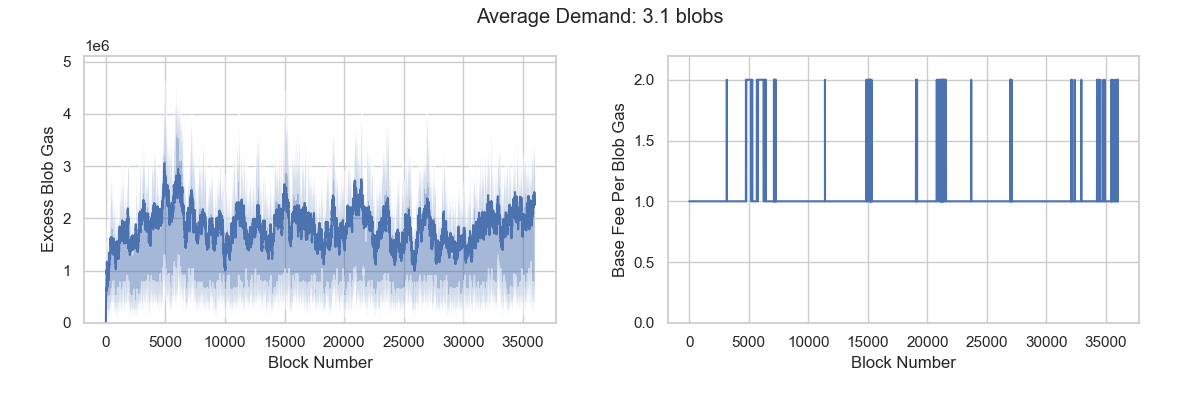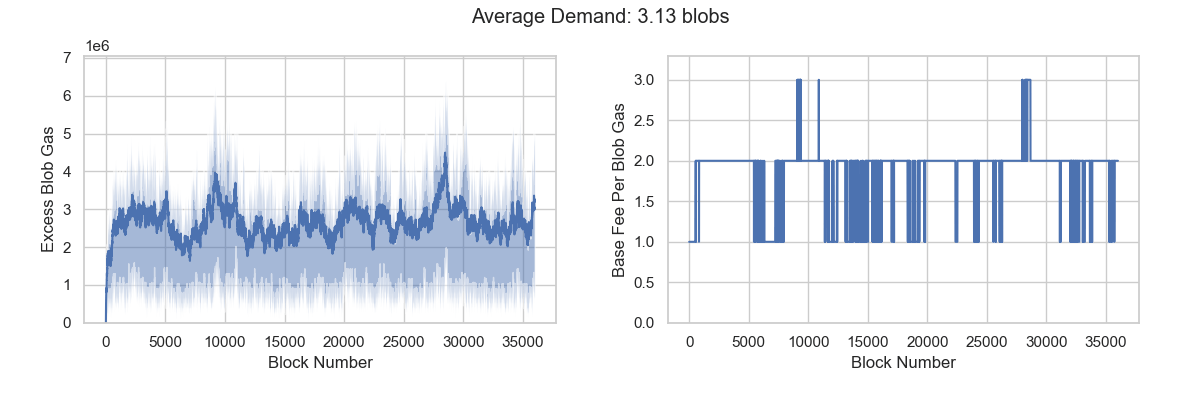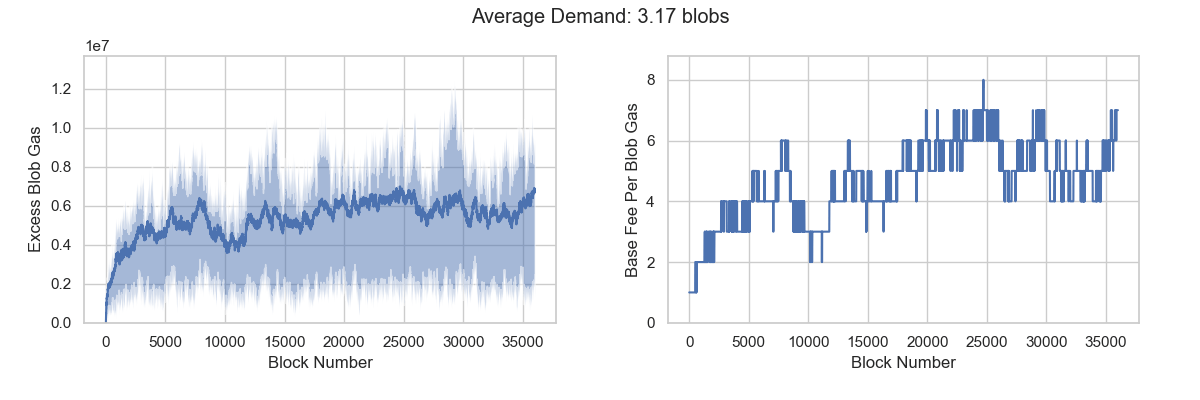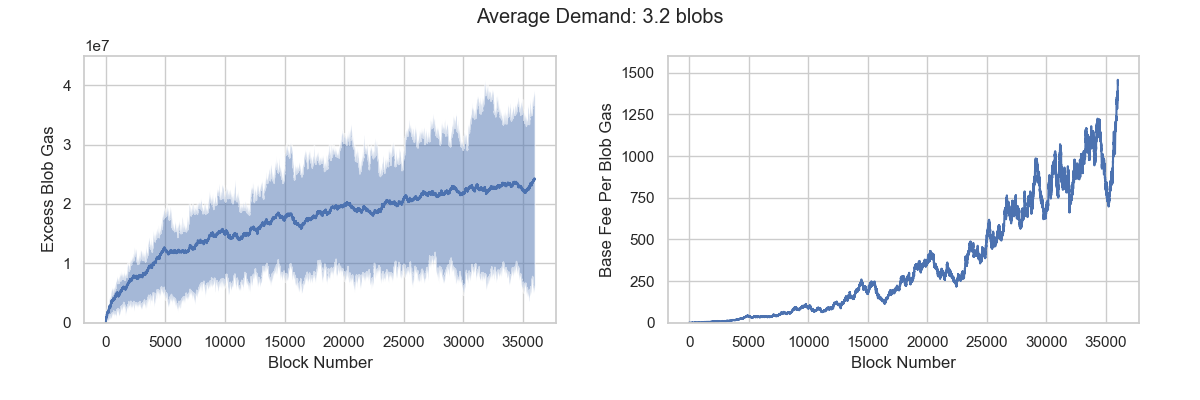
Target demand paradox

The pricing mechanism aims to control blob usage at a specific target value. However, a paradox emerges when this target falls outside the range of effective demand. In such cases, the blob fee market cannot reach equilibrium despite average blob usage approximating the target value, or equilibrium can only be achieved by consuming more blobs than the target specifies.

Demand variance represents another critical factor. As variance increases, the range of effective demand widens correspondingly. This explains why we achieve equilibrium in Scenario 4 and 5, where the target value falls within the expanded effective demand range.

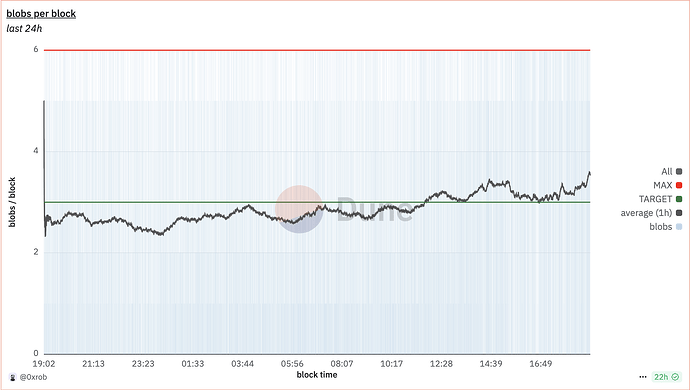
EIP-4844 status quo

Based on current data from Dune, the distribution of blobs_per_block more closely resembles Scenario 5. Optimistic rollups typically utilize 5 or 6 blobs, while ZK rollups prefer 1 or 2 blobs. This pattern has fortunately spared the Ethereum ecosystem from confronting the demand paradox.

However, demand must still remain within the effective demand range for 1.5-2 days to achieve market equilibrium. Unfortunately, we have yet to meet this criterion in the year following the EIP-4844 launch.

EIP-7691 Analysis

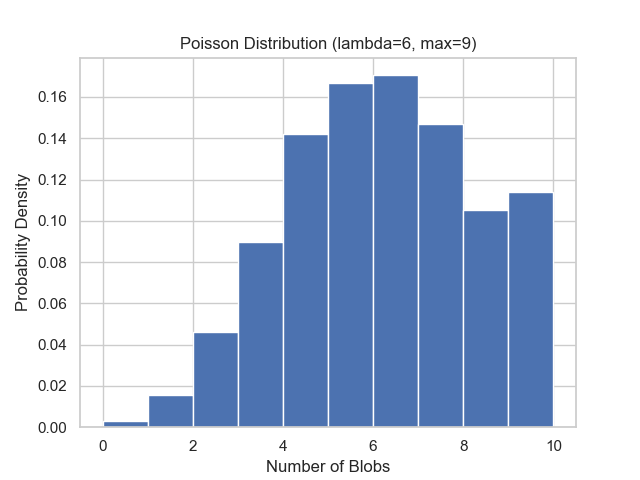
EIP-7691, scheduled for implementation in the upcoming Pectra fork, will increase the number of blobs per block to enhance Ethereum’s scalability through L2 solutions that depend on L1 data capacity. Under this proposal, MAX_BLOBS_PER_BLOCK will increase to 9, while TARGET_BLOBS_PER_BLOCK will increase to 6. The BLOB_BASE_FEE_UPDATE_FRACTION has been set at 5007716 to account for the asymmetry between target and maximum values.

The economic implications of these parameters on the blob fee market require thorough evaluation. We are conducting simulations under various demand variance conditions to determine the effective demand range under this new configuration.

In either case, excess_blob_gas fails to accumulate and base_fee_per_blob_gas remains fixed at MIN_BASE_FEE_PER_BLOB_GAS. This indicates that the target blob demand is insufficient no matter what variance is.

Our calculations place effective demand between 6.57 and 6.72 blobs, suggesting a high probability that the blob fee market will face the target demand paradox. When the market consumes an average of 6 blobs, it still cannot reach equilibrium or discover the fair price. To force the market toward equilibrium, consumption would need to exceed 6.57 blobs per block, significantly surpassing the target value.

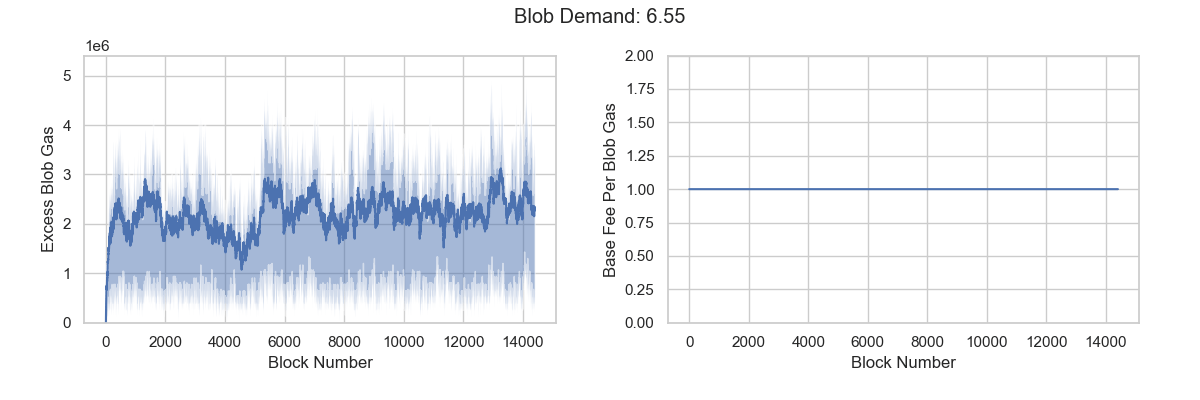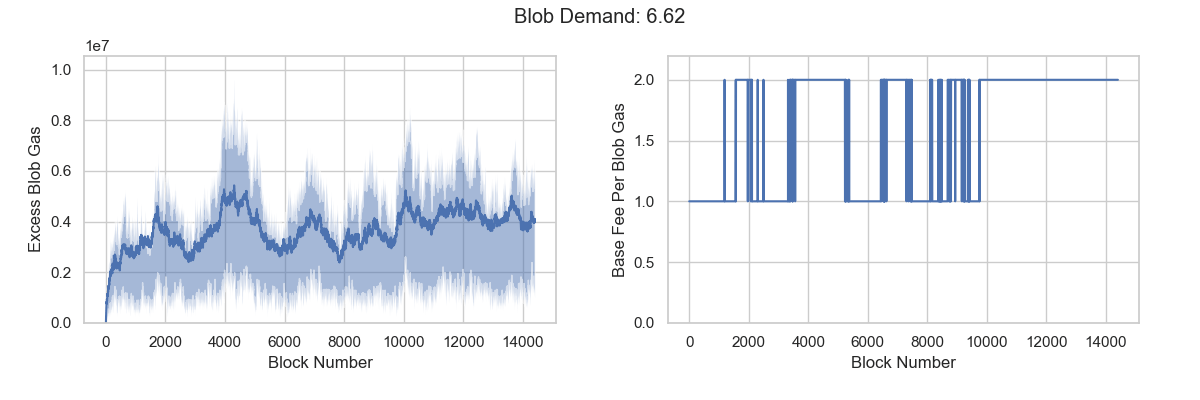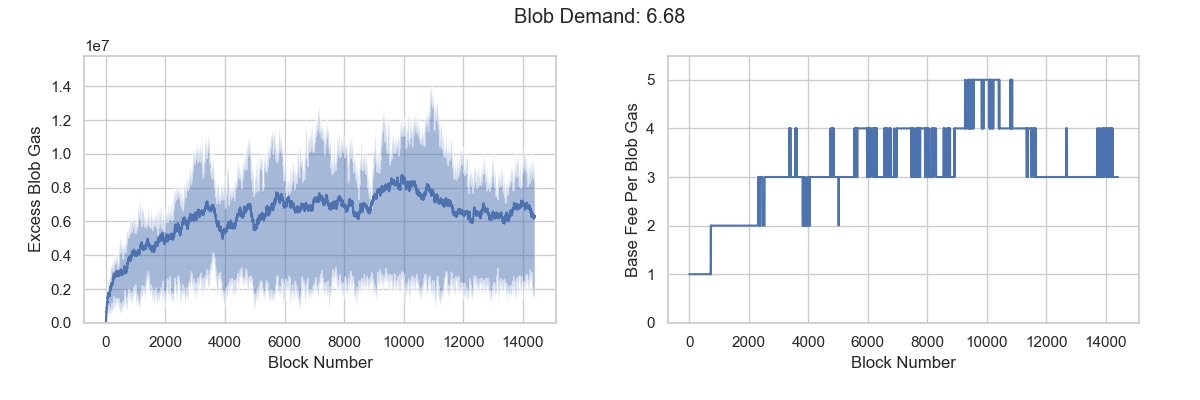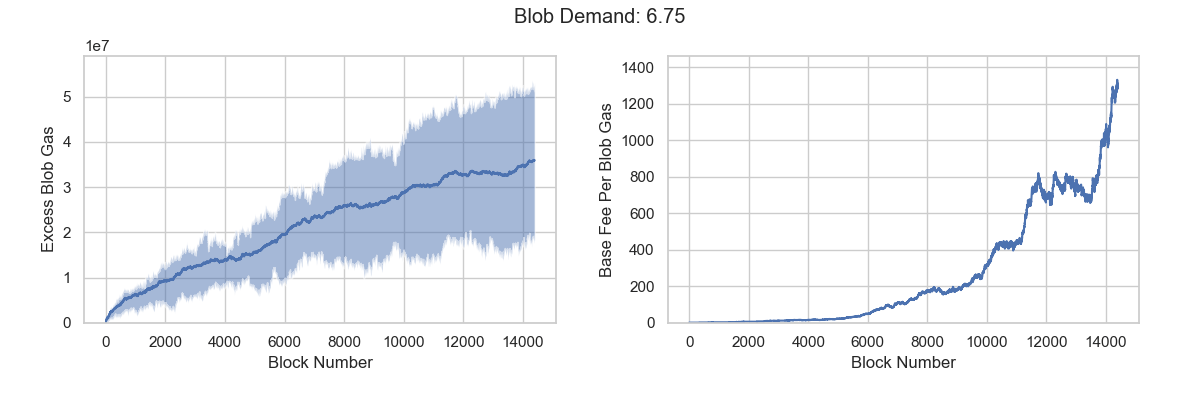
What can we do?

Idea 1: Making the base fee scaling symmetric ensures the mechanism stays as-is

To avoid the demand paradox, implementing symmetric base fee scaling is crucial. This approach would allow blob fees to scale by ±12.5% at the extremes of empty and full blocks. We should reconsider the parameters in EIP-7961, as the proposed changes might actually worsen the blob fee market’s current state. From an economic perspective, viable target/maximum blob configurations could be 4/8, 5/10, or 6/12

Idea 2: Increase minimum price

EIP-7762 proposes increasing MIN_BASE_FEE_PER_BLOB_GAS to accelerate price discovery for blob space. Let’s conduct a brief analysis.

We can define the cold-start time as the sum of demand growth time and price response time. Demand growth time represents how long it takes for blob demand to rise from 0 to the effective demand level. Price response time measures how quickly blob demand reflects in pricing. In simulated environments, setting a higher minimum price does reduce price response time. Conversely, this approach might impede demand growth.

However, no strong correlation exists between blob price and demand since blob demand functions as a derivative demand. Blob gas pricing doesn’t directly impact end users. Rollups may ultimately need to bear higher blob fees for Ethereum’s broader benefit.

Idea 3: Set a high initial value of excess_blob_gas

Determining a fair price for blob data is crucial in many aspects. A healthy blob fee market not only stabilizes public sentiment, thereby influencing ETH’s price, but also fosters greater confidence in the rollup-centric roadmap.

To efficiently discover this fair price, we can implement a mechanism similar to a Dutch auction by initially setting a high excess_blob_gas value, which translates to a high base_fee_per_blob_gas. This fee will gradually decrease until demand rises to meet the effective demand. While building demand from the ground up might take months, a Dutch auction-like process could potentially achieve price discovery within days.

References

• All simulations are run on the Jupyter Notebook
• EIP-4844
• EIP-7691
• EIP-7762

[kustrun]

Appreciate the time and effort you put into conducting and sharing this interesting research!

If I understand correctly, when target demand isn’t met, blob price equilibrium isn’t fully reached, which could mean rollup costs remain stable most of the time but can experience sudden exponential spikes?

I was also thinking—based on my understanding, isn’t this already the case today?

@Xiawpohr

This approach would allow blob fees to scale by ±12.5% at the extremes of empty and full blocks.

When blobs are empty, prices drop by approximately 12.5%, and when they’re full, they increase by the 12.5%

[Xiawpohr]

@kustrun

If I understand correctly, when target demand isn’t met, blob price equilibrium isn’t fully reached, which could mean rollup costs remain stable most of the time but can experience sudden exponential spikes?

In simulations, we calculate the expected value, weighted by the probability of each outcome, based on stable blob demand over a period of time. However, in reality, the expected value may not be present in the data, and demand constantly fluctuates.

In my view, actual blob demand remains low most of the time. Only at certain moments does it exceed the target value, leading to sharp price spikes, as described in Scenario 2 of the research. However, these spikes are short-lived and unsustainable.

@kustrun

I was also thinking—based on my understanding, isn’t this already the case today?

Yes, for now. However, after EIP-7691 is launched in the Pectra fork, MAX_BLOB_PER_BLOCK will be set to 9, while TARGET_BLOBS_PER_BLOCK will be 6. This breaks the symmetry in how prices respond to full and empty blob sections—when blobs are empty, prices decrease by ~14.5%, but when they’re full, they increase by only ~8.2%.

With this parameter configuration, the blob price is likely to stay at the lowest level for an longer period, even if average blob usage reaches the target.

[joeykrug]

That seems problematic that it’s even more lopsided now, reading your post option #3 (effectively a Dutch auction) seems like the most logical way to economically fix this issue.

How do you envision it working? Like would the excess blob gas start off high essentially as an auction to set the price before eip4844 mechanics kick in? Is the idea that you just do it once at the start to kick things off? If so, isn’t there a risk that effective demand goes below target for a while and then you end up back with the same problem of the market not finding equilibrium? Or do you think that’s unlikely once the market is kicked off in this manner?

It does seem like the min price should be increased too (idea #2), I remember eip-1559 had a min of 1 gwei, which makes more sense than 1 wei to me

[Xiawpohr]

@joeykrug

How do you envision it working? Like would the excess blob gas start off high essentially as an auction to set the price before eip4844 mechanics kick in? Is the idea that you just do it once at the start to kick things off? If so, isn’t there a risk that effective demand goes below target for a while and then you end up back with the same problem of the market not finding equilibrium? Or do you think that’s unlikely once the market is kicked off in this manner?

For this mechanism (idea #3) to work effectively, there must already be a stable demand for blobs to establish equilibrium. Otherwise, we’ll face the same issue, as you worried. Currently, blob usage has remained around 3 for a while, with no clear upward trend. I’m unsure whether demand will increase when the target becomes 6.

@joeykrug

It does seem like the min price should be increased too (idea #2), I remember eip-1559 had a min of 1 gwei, which makes more sense than 1 wei to me

EIP-1559 had a initial price of 1 gwei, but this was not a minimum price. EIP-4844 just adopts an exponential form of the EIP-1559 pricing mechanism. We didn’t encounter this problem back then because the market demand was driven by the DeFi summer and NFT mania, making gas consumption exceeds the target a lot.

[hanniabu]

Would this continue to be an issue at 48/72 blobs (year end target)? If I’m understanding your post correctly, it sounds like this is an issue with being such low scale, but might not be an issue as the blobs are greatly increased.

[TimDaub]

Why don’t you list as a mitigation ideas to leave the blob target as is for now, or to increase the blob target by fewer blobs?

[Xiawpohr]

@hanniabu

Would this continue to be an issue at 48/72 blobs (year end target)? If I’m understanding your post correctly, it sounds like this is an issue with being such low scale, but might not be an issue as the blobs are greatly increased.

Your thought might be correct. I conducted a simulation with 48/72 blobs, and the results indicate that the target value falls within the effective demand range.

So, I decided to dive a little deeper. Let’s take a look at the Poisson distribution. With λ = 48 in the range [0, 72], the distribution appears symmetric around 48. In contrast, with λ = 6 in the range [0, 9], the distribution is asymmetric around 6, with the right tail cut off. This explains why having 48/72 blobs in the simulation wouldn’t cause an issue.

The variance of demand is also a crucial factor in the pricing process. Assuming demand follows a Poisson distribution, issues may arise when mean_of_demand + 3 * std_of_demand > max_value. Based on this, we can infer the following configuration.

• 6/9 → could be an issue
• 12/18 → could be an issue
• 24/36 → could be an issue
• 48/72 → might be okay

On the other hand, the Poisson distribution is merely a mathematical tool and serves as the best case when demand follows this distribution. However, we must also consider other cases.

Let’s assume the status quo continues, where some blocks consume full blobs while others consume none. With the 48/72 configuration, 67% of blocks must consume full blobs to reach market equilibrium. In contrast, with a symmetric configuration, only 50% of blocks need to do so. This suggests that an asymmetric blob configuration requires higher blob consumption in most of the time.

[Xiawpohr]

It’s a conservative approach to keep the target unchanged or increase it by only a few blobs. I understand your concerns, but the current public sentiment calls for Ethereum to accelerate. As a researcher, my purpose is simply to ensure that we accelerate Ethereum in a more aligned and sustainable way.

[TimDaub]

@Xiawpohr

As a researcher, my purpose is simply to ensure that we accelerate Ethereum in a more aligned and sustainable way.

That’s fair. That said, I don’t share your analysis of what the public wants:

@Xiawpohr

I understand your concerns, but the current public sentiment calls for Ethereum to accelerate

I think the public wants ETH to be a valuable asset again by accruing as much fees as before when the EIP-4844 merge happened. Nobody is currently served by creating more capacity. The chain isn’t at capacity and this is proven by the fact that L2 transactions are fractions of a US Dollar cent.

You wrote as your Introduction/Motivation:

@Xiawpohr

As expected, rollup costs have dropped significantly due to the cheaper ‘blob’ resource. However, the overall price of blobs has remained exceptionally low for an extended period, raising concerns within the community about whether rollups are contributing enough to the mainnet.

So here we have it. You’re actually agreeing that current fee accrual is insufficient. So I don’t understand why it isn’t part of the research to understand whether more competition for the current blob limit would give us back greater fee accrual. I’d personally favor that way more than yet more “experiments in production” to fix an issue that should have never been put there.