Time-locked 1:1 tokens as rudimentary pseudo-futures

Economics
1

“Native futures”

Native (perpetual) futures (without a funding-rate).

A sketch of a system to enable liquid markets for the price of ether in the future. The system is perpetual in that futures do not have to expire. There is no requirement for a system to assign a funding-rate as in current perpetual futures markets.

TLDR: Lock ether to mint a range of ERC20 tokens (1:1) that enforce a delay upon unlocking. Trade the tokens freely as an expression of future price prediction.

This is an invitation for comment and criticism. Please share any existing similar work that comes to mind.

Background

  • Futures markets increase the efficiency of markets
  • Current off-chain futures markets rely on legacy systems that hold user keys
  • Some on-chain futures markets in design make use of oracles
  • Some have staking tokens that incentivise risk minimisation of the system

Inspiration

  • With smart contracts, you can ensure the delivery of capital occurs at a time in the future.
  • Every free market participant is an oracle, in that their action brings information about the world into the market. A system that uses every participant to create price information is stronger than a system with special dedicated oracles.
  • Free agents can audit a system of smart contracts. The simpler the mechanism, the easier the risk assessment.

Goal

  • Create a continuous futures market that integrates with existing infrastructure
  • Mechanisms include locking ether for later redemption after a time delay
  • The time preference of users, and their perception of future prices will create a market with a differential between ether locked for different durations
  • There is no time-critical nature to the market. Futures are always redeemable with a delay that is user-initiated and non-compulsory.
  • No oracle

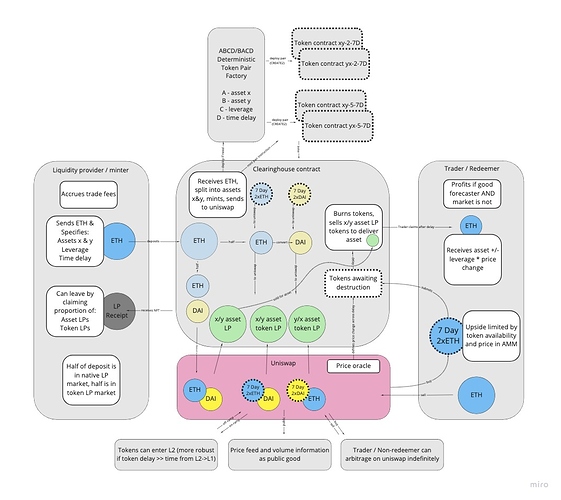
Architecture

  • Base contract accepts ether and locks it, returning ERC20 token
  • User can return ERC20 token to redeem ether 1:1
  • Base contract will delay the redemption of ether by a fixed delay, depending on the ERC20 token
  • When locking ether, the contract can issue a range of ERC20 tokens that correspond to different delays. When the ERC20 is returned, the contract will delay the delivery of ETH by the corresponding number of days from the moment of return. The proposed set of ERC20 contracts is:
    • 1 day (ETH001DAY)
    • 2 day (ETH002DAY)
    • 3 day (ETH003DAY)
    • 4 day (ETH004DAY)
    • 5 day (ETH005DAY)
    • 6 day (ETH006DAY)
    • 7 day (ETH007DAY)
    • 14 day (ETH014DAY)
    • 28 day (ETH028DAY)
    • 90 day (ETH090DAY)
    • 180 day (ETH180DAY)
    • 270 day (ETH270DAY)
    • 360 day (ETH360DAY)
    • 720 day (ETH720DAY)
  • When locking ether and minting delayed ether tokens, the user submits the quantity of each token desired, where the sum is equal to the ether provided (e.g. 1 ETH is locked to mint 0.5 ETH005DAY and 0.5 ETH014DAY).
  • In its simplest form, a user may lock 1 ETH and mint 1 ETH360DAY. They may then transfer this to another person who can immediately submit the 1 ETH360DAY to the base contract. 360 days later that person will receive 1 ETH.
  • It is up to the market to decide what each token is worth at any point up until it is returned to the base contract for destruction and redemption for ether.

Time delayed withdrawal mechanism

Time delay is an approximation based on block speeds. This is an obvious pain point. A prolonged period of delayed or accelerated blocks would cause ether to be available earlier or later than expected.

Delayed-ether is be sent to the base contract along with an address where the ether will be redeemed to. The contract has a hard coded value for the average block time. The contract registers the quantity of ether, the address and calculates the block height after which the ether may be withdrawn.

The contract must then be called after the delay has passed so that the ether is sent from the contract. Two ways this could go ahead: individual calls for individual balances; or anyone can call the contract at any time to release all funds that have passed their delay duration.

Market incentives

A person sees a market where they disagree about the future price of ether. Depending on the situation they may:

  • Lock ether, mint delayed-ether then sell it in that market
  • Buy the delayed-ether in the market and return it to the contract, receiving ether upon completion of the delay.

Use cases

Believe ether price will be higher at future time

  • Buy delayed-ether (at a discount from bears), send to base contract, wait for ether to arrive.

Believe ether price will be lower at future time

  • Deposit ether to mint delayed-ether, sell in market at a premium.

Believe ether price will be volatile during future period

  • Deposit ether and mint a range of delayed-ether. Provide liquidity in markets where people are trading delayed-ether.

Believe ether price will not be volatile during future period

  • I am unsure of how agents would utilise the system to their advantage here.

Scaling

The contract may benefit from scalability solutions that other markets develop and deploy. Because these futures never expire, traders could exchange delayed-ether in layer 2 markets indefinitely. Cheap layer 2 markets could lead to more trades and more smooth price-finding.

Having >10 individual ERC20 contracts as part of the system seems unavoidable. Can you see a simpler arrangement?

Security

The system operates without reliance on external actors to maintain the platform. If the system falls into disuse, every single token may be redeemed for ether. The cost incurred by users in this instance is the opportunity cost of locked capital.

For a contract with few moving parts, the security lies in the ease of auditing the contract.

At deployment, the contract contains the whitelisted addresses of the deployed ERC20 ETHxxxDAY contracts. No additional contracts can be added after deployment.

Each ERC20 ETHxxxDAY contract will only mint in response to requests from the whitelisted base contract.

Trading costs

The following steps incur costs

  • Deposit ether to mint delayed ether
  • Transfer or trade delayed-ether (standard ERC20 costs)
  • Sending delayed-ether to layer 2 (optional with unknown costs)
  • Returning delayed-ether to unlock ether
  • Making a contract call to withdraw ether

Upgradability

Not possible. Deployment of a separate contract and users would exit the old system and enter the new system.

Referral field

This is an idea that I wish I had seen for other major projects. Including this function in the base contract can provide an example for the broader community to play with, as a solution for other projects.

The concept is to provide a reward for systems to be built around the contract.

When interacting directly with the contract, there is no fee by default. A fee can be triggered during the contract call by the caller, for example a front-end for the contract. The contract would respond by taking a small percentage (e.g. ~0.01%) of the ether entering (or leaving) the contract.

Calling the referral field enables a front-end service to meet development and maintenance costs. The referral fee, if invoked, could also be divided into audit and deployer funds.

Audit funds

None by default.

Optional: The deployer of the original base contract could specify an address of a known public auditor for a fraction of the opt-in referral fee. Once the amount reaches a viable threshold, the auditor could withdraw the funds and perform and audit. (Or withdraw the funds and not perform and audit, but lose credibility. Or withdraw the funds and send them to a different auditor who is willing to do the work.) If an auditor address is in the base contract, but there has not been sufficient volume to perform and audit, interested parties could either do an audit as a public good, or donate funds so that an audit becomes viable.

Deployer reward

None by default.

Optional: The deployer of the original base contract could specify an address for a fraction of the opt-in referral fee. Given that this project is not likely to be very large, this is more about demonstrating ways that other developers could create systems that sustain the creators, and prevent capture by venture capital. In an ideal world venture capitalists are designing and deploying beautiful systems that are so useful that they can make money by taking a small fee as compensation.

Synthetics built from delayed-ether

As an ERC20, the delayed-ether may be wrapped in a variety of ways to create custom financial instruments. Because there is no counterparty risk, wrapped assets do not have to worry about solvency in the underlying delayed-ether system.

Leveraged trading

There is no provision for leverage, however people may create leveraged positions elsewhere to then interact with this system. Importantly, the use of leverage does not introduce risk to the system. This is because the base contract accepts ether, not assets that are created from leverage that are vulnerable to collapse.

Flash loans

No significant risk is foreseen. The architecture of a flash loan involving delayed-ether is as follows:

  1. Transaction begins
  2. Leverage acquisition
  3. Trade for ether
  4. Send ether to base contract
  5. Mint delayed-ether
  6. Dispose of delayed-ether in market
  7. Other trading activity
  8. No further interaction with delayed ether
  9. Leverage is unwound
  10. Transaction ends
  11. A third party, now in possession of delayed-ether may trade it or redeem for ether.

Step 6 lowers the price of delayed-ether. This would disrupt any contract that uses the spot market price for delayed ether as an oracle. Mitigation can be achieved by those contracts using average price feeds.

Broader impact

If the system becomes widely used, the future price of ether can be taken from a range of markets where delayed-ether is trading. Other systems can use these markets as oracles. Individuals can hedge risk with systems that they can examine and reason about and can avoid taking counterparty risk.

Limitations

In general this feels like a naive approach. Are there game theoretic flaws? Are there enough incentives for participants? Is there a better term for a financial instrument like this?

Many features could be added, but there is a high preference for simplicity.

What do you think?

3 Likes
2

ummm … sandy … this is BRILLIANT!!!

well done. Such an elegant solution to a clear need. Can totally see this morphing into an ERC standard of its own. Not naive at all, your “high preference for [unstructured] simplicity” has a rich provenance. Really great.

wrt what you identify as an obvious pain point, why not solve the pain by relying on a UTC-style universal date:time oracle?

can’t wait to play around with LockEth (?) – :wink: :smiley_cat:

3

Holding time-locked ether is strictly worse than holding regular ether. Why would anyone time-lock their ether to receive a strictly inferior token in return?

1 Like
4

Thank you for your responses

Cleanapp, for your suggestion of a time oracle I have these thoughts:

  • A time oracle introduces complexities during congestion that I would prefer to avoid. Will time be available if block space is scarce and expensive?
  • I am leaning toward using a fixed block time estimate (14 seconds) and committing to future block heights as a proxy for real world delay. During changes to block time, such as the difficulty bomb activation, these will not map to real time well. However, it would be public knowledge and participants reason that a 7 day delay is really going to be a 9.5 day delay, and trade accordingly.

vshvsh, I accept that the above system lacks incentive for rational traders

  • You correctly point out that an asset locked as a token which can be redeemed for the original asset at a future date is of no use.
  • The system I outlined is more fundamentally flawed, in that there is no intrinsic comparator for value. One token may increase in value, but there must be a unit of account. I have revised my design considerably and outline it below.

TLDR: An open protocol that uses uniswap LP tokens as collateral to generate tokens that can be used as a delayed trade commitment. A clearinghouse contract will execute a trade and return a multiple of the gain or loss. The public nature of the market creates an oracle that exposes granular market sentiment about future prices.

Design updates

In this revision, the system becomes coupled with uniswap to create an autonomous clearinghouse. Leveraged returns are introduced as the incentive for participation.

The protocol consists of ERC777 (ERC20 compatible) tokens that can be submitted to the clearinghouse which, after a delay, executes a leveraged trade on uniswap and delivers an asset.

While the system can be generalised to any token pair (e.g. ETH/tBTC) and any delay, consider a system with:

  • WETH (wrapped ether)
  • DAI
  • 7 day delay
  • 2x leverage

The WETH and DAI are locked as reserves to free delayed-WETH and delayed-DAI. These can be sold and traded freely. If a delayed-token is redeemed at the clearinghouse, after 7 days the leverage trade profits or losses are able to be claimed by the trader.

For example

  1. 1 delayed-WETH is sent to the clearinghouse
  2. Clearinghouse records the DAI:WETH rate
  3. 7 days pass
  4. The trader claims their trade
  5. The clearinghouse calculates the percentage gain/loss, applies the leverage, obtains that amount from uniswap, sends to the trader.

The clearinghouse loses money when the trader is successful and makes money when they are not. To mitigate the risk of losing funds, all locked funds are used to provide liquidity in the underlying uniswap markets. Capital allocation is explained in detail below, but the main outcomes are that:

  • The clearinghouse benefits from trades between delayed-assets
  • Locked capital is not idle
  • The amount of delayed-tokens that can be bought at market is limited by the amount in circulation.
    • The uniswap constant-product AMM raises prices quickly when token liquidity is low. A trader cannot cheaply buy all the tokens and submit them to the clearinghouse without spending a lot of money.
    • As the delayed-token market grows, more liquidity enables larger trades.

Formula for redemption

If a trader submits a delayed-token, the amount of the actual token received is a function of the exchange rate initially, exchange rate after the delay and the amount of leverage they have.

received = 1 + leverage *(\frac{Final Rate}{Initial Rate}-1)

That is, the gain or loss is multiplied by the leverage and then added/subtracted from the number of tokens they had.

E.g. for a a 2x WETH/DAY 7 day futures market. One token was bought by the trader and submitted to the market.

Scenarios

  • Initial price 300 DAI/WETH, then after one week the price is 200 DAI/WETH. (price drop of 30%)
    • received = 1 + 2 *(\frac{200}{300}-1) = 1 + 2 *(-\frac{1}{3}) = \frac{1}{3} = 0.33 WETH
    • Equivalent to 0.33*200 = 66 DAI
  • Initial price 300 DAI/WETH, then after one week the price is 400 DAI/WETH. (price rise of 30%)
    • received = 1 + 2 *(\frac{400}{300}-1) = 1 + 2 *(\frac{1}{3}) = \frac{5}{3} = 1.67 WETH
    • Equivalent to 1.67*400 = 666 DAI

In each situation, the absolute return depends on how much those tokens were purchased for. If the market had mispriced them, both both situations could have been good/bad deals.

Locked Capital

Delayed tokens are released from the clearinghouse as pairs in an atomic transaction in which:

  • A person sends ether to the clearinghouse
  • The clearinghouse converts the ether to 50:50 WETH:DAI in uniswap
  • The WETH and DAI are deposited in uniswap as liquidity
  • Liquidity Provider (LP) tokens are withdrawn to the clearinghouse
  • The contract releases an equal number of 7-day-delayed-WETH and 7-day-delayed-DAI
  • The 7-day-delayed-WETH and 7-day-delayed-DAI are sent to a new pool on uniswap as liquidity
  • Liquidity Provider (LP) tokens for the delayed tokens are withdrawn to the clearinghouse.

The person supplying capital retains proportional rights to the clearinghouse assets, which when they withdraw would be returned as ether along with any other token, such as UNI governance tokens the clearinghouse accrued.

Removal of capital from the protocol would cause the following actions:

  • Their share of delayed-token LP tokens returned to delayed market
  • Their share of LP tokens returned to delayed market
  • Assets (WETH, DAI) converted to ether
  • Ether and governance tokens returned to the original supplier of capital

Fair Market Evaluation of Delayed Tokens

What should be the baseline price for a given leveraged delayed token?

Ignoring fees for the moment, what is the fair TokenPrice (the value relative to the initial asset price) that gives breakeven return (ignoring fees)?

TokenPrice = AmountRedeemed

The market should be able to calculate the fair value price of each token based on:

  • Leverage. Multiplier on the percentage change in value.
  • Asset (used for accounting (e.g. DAI or WETH)). Here we use DAI as the unit of account.
  • Ratio (of final price to current price, quoted in the asset of account). \frac{FinalPrice}{InitialPrice}

TokenPrice = AmountRedeemed = 1 + leverage*(ratio-1)

e.g. If ratio is 1.33x (e.g. ether price moves from 300DAI/WETH to 400DAI/WETH).

In words, the amount of ether you would receive from the clearinghouse for each delayed-token is the real asset +/- any percentage change (e.g. 33%) in the price, multiplied by the leverage of that particular token type (2x). In this situation (0.33 * 2 = 0.66) an extra 66% of that asset.

TokenPrice = 1 + leverage*(ratio-1)

TokenPrice = 1 + leverage*(0.33)

Relative to the current price of ether (300 DAI/ETH), the delayed-WETH TokenPrice at different leverages should be roughly:

  • One 2x-delayed-WETH: 1.66 ETH (or 500 DAI)
  • One 5x-delayed-WETH: 2.65 ETH (or 790 DAI)
  • One 10x-delayed-WETH: 4.30 ETH (or 1290 DAI)

Those are the prices that would be rational if the market participants believed that in 7 days the prices was going to rise from 300 to 400 DAI/ETH.

Oracle Provision

While the above calculations are of use for traders who have strong ideas about future prices, consider an individual looking at the delayed-token marketplace on uniswap.

If the market is public, has rational economic actors and has reasonable amount of liquidity and participation, the prices in the market represent what rational actors believe about the future.

The equation from above:

TokenPrice = 1 + leverage*(ratio-1)

Can be rearranged:

TokenPrice = 1 + leverage*(ratio-1)

ratio = \frac{TokenPrice - 1}{leverage} +1

Where ratio = \frac{FinalPrice}{InitialPrice},

\frac{FinalPrice}{InitialPrice} = \frac{TokenPrice - 1}{leverage} +1

Gives a formula for calculating the future price (FinalPrice) of ether:

FinalPrice = InitialPrice*(\frac{TokenPrice - 1}{leverage}+1)

If a non-trader member of the community looks at the 5x-7-day-delayed-WETH market on uniswap and sees that each token is worth $802, but the current price of ether is 340, what can they determine?

Inputs:

  • InitialPrice: 340
  • TokenPrice: 802 / 340 = 2.36
  • Ratio: 5

FinalPrice = 340*(\frac{2.36 - 1}{5}+1)

FinalPrice = 340*1.27 = 431

They can determine that the participants in that uniswap market are currently considering 431 DAI/ETH to be a fair value for 1 ether in 7 days time.

Whether that manifests is not certain. What can be said though, is that it can provide a measure of market sentiment, at specific time points in the future. Traders who have more accurate predictions can participate and profit, and thereby alter the market and provide a better estimate of the future.

Using the uniswap dealyed-token price feed as an oracle for future prices might provide a utility for another project.

Tokens Supported

Use a token factory where anyone can create new pairs with different delays and leverages. Good first candidates might be widely used tokens and tokens with very few trust assumptions:

  • DAI (2x, 5x, 10x)
    • 2x-7D-WETH-DAI
    • 2x-7D-DAI-WETH
    • 2x-14D-WETH-DAI
    • 2x-14D-DAI-WETH
  • tBTC (2x, 5x, 10x)
    • 2x-7D-WETH-tBTC
    • 2x-7D-tBTC-WETH
    • 2x-14D-WETH-tBTC
    • 2x-14D-tBTC-WETH

The corresponding pairs on uniswap could be:

  • 2x-7D-WETH-DAI and DAI
    • Delayed WETH per current DAI. A trader could use DAI to buy the token.
  • 2x-7D-DAI-WETH and WETH
    • Delayed DAI per current WETH. A trader could use WETH to buy the token.

There may be more optimal solutions for how to lock the original capital. Two candidates are:

  • The capital is locked in normal pools and then the LP tokens used to mint delayed tokens, which are then deposited into a single delayed-token / delayed-token pool.
  • The capital is used to generate the token and separate pools are made, with each pair having one normal token and one delayed-token.

Redemption Procedure

When minters/capital providers initially lock up capital, they put their WETH/DAI in those pools. When someone redeems one 2x-7D-WETH-DAI, the clearinghouse records the price of WETH/DAI now, and then a week later repeats the pricing, then calculates the win/loss and then withdraws enough LP tokens from the pool (2x-7D-WETH-DAI / WETH) to give them their WETH.

Drainage Attack

The capital providers of the system:

  • Gain capital from
    • Trading fees
    • Traders who make incorrect predictions about the future when redeeming tokens
  • Lose capital from
    • Impermanent losses in broad price changes
    • Traders who make correct predictions about the future

Consider a trader (or group of traders) who make repeated large volume token redemptions, at high leverage, and who is correct in their predictions about price movement. Over time the liquidity tokens are depleted by the trader. Original capital providers wishing to claim their capital would be at a loss unless there are a greater number of inaccurate trades.

In general, the action of any trader purchasing or selling tokens moves the price and reduces the efficiency of their trading. This is increasingly true where the magnitude of the trade approaches the magnitude of the liquidity pool. That is to say that if the pool is small, a trader who can predict the future can only make a small amount of money before tokens become prohibitively priced by the AMM. Conversely, if the liquidity pool is large, a small trader who can predict the future may profit, but will not make a significant impact to the pool reserves.

Clearinghouse Swap Frontrunning

The trader claiming funds calls the clearinghouse after 7 days. The clearinghouse executes a market buy of the asset to give to the trader in that same transaction. A frontrunner can see the market-buy in the mempool and increase the price of the asset (WETH or DAI), let the contract make the trade, then arbitrage the difference in the asset price from prices in ther markets.

For small trades in liquid markets, this is not profitable. In large trades this may be in the traders interest to prevent this.

Solution: allow an opt-in TWAP.

  • After the 7 day delay is finished, the contract allows anyone to record the current price of an asset in the relevant market (e.g. record the DAI/ETH rate in contract storage). Then, when they make their claim at their funds, the contract uses the TWAP for that window to determine the price and perform a uniswap transaction based on that. To manipulate the market someone would have to elevate prices in a more prolonged and strategic manner. Multiple TWAP checkpoints could protect and extremely large trade. The ability to commit TWAP checkpoints could be opened a few hours prior to the end of the period to allow for confident on-time withdrawl
  • The TWAP checkpoints could be submitted by anyone, including those who are liquidity providers to the system. If they saw that the system was going to make a large trade, they could reduce the risk of the trader manipulating the market for their own gain.

Interfaces and analysis

I like the idea of a marketplace where the strength of peoples convictions can be inspected. Imagine aggregating the values of token prices and graphing what the market believes, and how much capital is behind those beliefs. If you store the data you could provide some interesting comparisons between the projected and real prices. Would it show any interesting features when compared to the timing of announcements and releases?

One nice feature would be to have a really descriptive summary of current token prices. For example: The market is pricing the tokens at $x, which implies an expected price of $y for the asset in 7 days. If you think the price is going to be (enter value here), the token should be worth $z. If you bought a token at this price, see below for the amount you would receive at different prices in 7 days, and what absolute return that would correspond to.

Closing thoughts

The introduction of delayed purchases (rather than simple locks) increased the complexity. I think the design is still simple enough to be appealing and it would be cool it it worked.

Next steps:

  • Examining whether there are still major incentive problems
  • Describing the protocol more clearly
  • Maybe some modelling, perhaps with cadCAD
  • Thinking about what contract architecture might work

I again welcome your thoughts and feedback!

1 Like
5

thank you for developing this idea further, and the revisions. haven’t had a chance to go through this in detail (including the leveraging mechanics), but wanted to offer the newly-released $based rover scripts as good comparative case studies for the utility of time-lock functions. Moonbase was launched a few days ago, and the first “rovers” are set to go live at any moment.

With respect to underlying incentives, I think the intuition that you described in the OP and in the revision will be proven right in deployment, even without the leveraging component. That is, the higher the composability (several “standardized”-length locking periods --> purely user-defined time-lock periods) the higher the resulting utility.

What you’re describing seems to be a critical missing piece in a general-purpose user-defined options+futures market, where any person can create any [duration] option for any token. As mentioned in the first response, … brilliant!

6

Here is a diagram that lays out the structure of the second iteration:

monodiagram
monodiagram1059×943 145 KB

2 Likes