Summary
I propose a construction, based on Lamport’s 99% fault tolerant consensus ideas, that I call timeliness detectors. Timeliness detectors allows online clients (ie. clients, aka users, that are connected to other clients with latency \le \delta) to detect, with guarantees of correctness and agreement, whether or not blocks were published “on time”. In the event of a 51% attack, this allows at least the subset of clients that are online to come to agreement over (i) whether or not a “sufficiently bad” 51% attack happened, and (ii) what is the “correct” chain to converge on and potentially even (iii) which validators to “blame” for the attack. This reduces the ability of 51% attacks to cause chaos and speeds up recovery time from an attack, as well as increasing the chance that a successful attack costs money.
Timeliness detectors
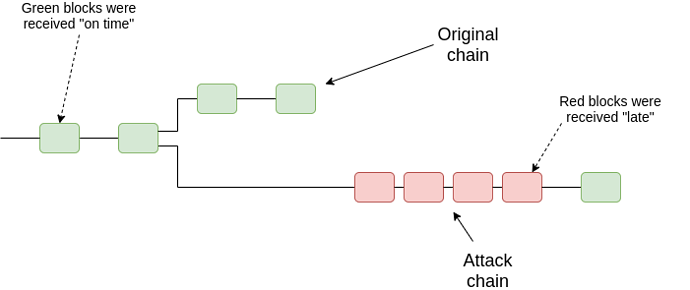
The most basic construction for a timeliness detector is as follows. For every block that a client receives, the client maintains a “is it timely?” predicate, which states whether or not the client thinks the block was received “on time”. The goal of this will be to try to distinguish the attacking chain from the “correct” chain in a 51% attack:
Our model will be simple: each block B has a self-declared timestamp t (in real protocols, the timestamp would often be implicit, eg. in the slot number). There is a commonly agreed synchrony bound \delta. The simplest possible timeliness detector is: if you receive B before time t + \delta, then you see the block as timely, and if you receive it after t + \delta, then you do not. But this fails to have agreement:

We solve the problem as follows. For each block, we randomly select a sample of N “attesters”, v_1 ... v_n. Each attester follows the rule: if they see a block B with a timestamp t along with signatures from k attesters before time t + (2k+1)\delta, they re-broadcast it along with their own signature. And the rule that a client follows is: if they see a block B with a timestamp t along with signatures from k attesters before time t + 2k\delta, they accept it as timely. If they see B but it never satisfies this condition, they see B as not timely.
Let us see what happens when even one client sees some block B as timely, though others may not see it as timely at first because of latency discrepancies. We will at first assume a single, honest, attester.
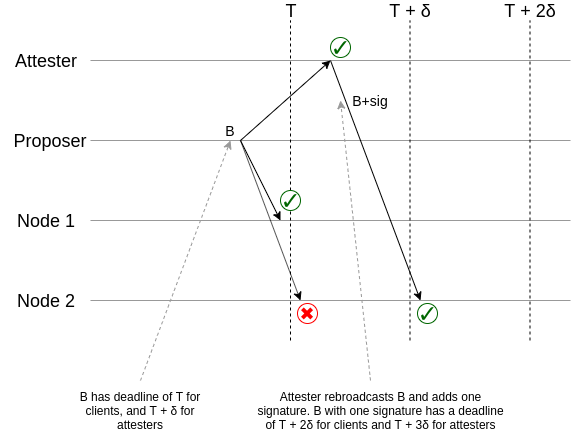
This diagram shows the basic principle behind what is going on. If a client sees a block before for deadline T, then (at least because they themselves can rebroadcast it) that block will get into the hands of an attester before the attester deadline T + \delta, and the attester will add their signature, and they will rebroadcast it before time T + \delta, guaranteeing that other nodes will see the block with the signature before time T + 2\delta. The key mechanic is this ability for one additional signature to delay the deadline.
Now, consider the case of n-1 dishonest attesters and one honest attester. If a client sees a timely block with k signatures, then there are two possibilities:
- One of those k signatures is honest.
- None of those k signatures are honest (so one attester who has not yet signed still remains)
In case (1), we know that the attester is honest, and so the attester broadcasted B with j \le k signatures before time T + (2j-1)\delta, which means that (by the synchrony assumption) every client saw that bundle before time T + 2j\delta, so every client accepted B as current.
In case (2), we know that the honest attester will see the bundle before time T + (2k+1)\delta, so they will rebroadcast it with their own signature, and every other client will see that expanded bundle before the k+1 signature deadline T + (2k+2)\delta.
So now we have a “timeliness detector” which a client can use to keep track of which blocks are on time and which blocks are not, and where all clients with latency \le \delta to attesters will agree on which blocks are timely.
The Simplest Blockchain Architecture
Come up with any rule which determines who can propose and who attests to blocks at any slot. We can define a “99% fault tolerant blockchain” as follows: to determine the current state, just process all timely blocks in order of their self-declared timestamp.
This actually works (and provides resistance to both finality-reversion and censorship 51% attacks), and under its own assumptions gives a quite simple blockchain architecture! The only catch: it rests everything on the assumption that all clients will be online and the network will never be disrupted. Hence, for it to work safely, it would need to have a block time of perhaps a week or longer. This could actually be a reasonable architecture for an “auxiliary chain” that keeps track of validator deposits and withdrawals and slashings, for example, preventing long-run 51% attacks from censoring new validators coming in or censoring themselves getting slashed for misbehavior. But we don’t want this architecture for the main chain that all the activity is happening on.
A more reasonable alternative
In this post, however, we will focus on architectures that satisfy a somewhat weaker set of security assumptions: they are fine if either one of two assumptions is true: (i) network latency is low, including network latency between validators and clients, and (ii) the majority of validators is honest. First, let us get back to the model where we have a blockchain with some fork choice rule, instead of just discrete blocks. We will go through examples for our two favorite finality-bearing fork choice rules, (i) FFG and (ii) LMD GHOST.
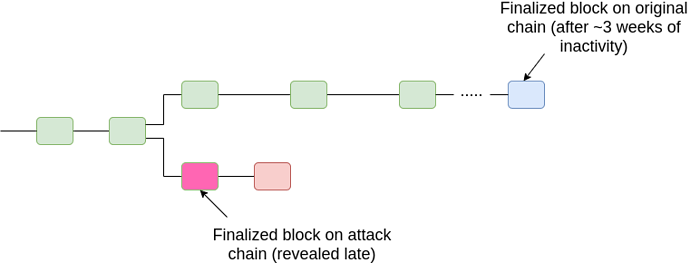
For FFG, we extend the fork choice rule as follows. Start from the genesis, and whenever you see a block with two child chains which are both finalized, pick the chain with the lower-epoch timely finalized block. From there, proceed as before. In general, there will only ever be two conflicting finalized chains in two cases: (i) a 33% attack, and (ii) many nodes going offline (or censoring) leading to a long-running inactivity leak.
Case (i):

Case (ii), option 1 (offline minority finalizing later):
Case (ii), option 2 (offline majority, later reappearing with finalized chain):
Hence, in all cases, we can prevent 51% attacks from breaking finality, at least past a certain point in time (T + 2k\delta, the time bound after which if a client has not accepted a block as timely then we know that it will never accept it as timely). Note also that the above diagram is slightly misleading; what we care about is not the timelines of the finalized block, but rather the timeliness of a block that includes evidence that proves that the block is finalized.
For clients that are offline sometimes, this does not change anything as long as there is no 51% attack: if the chain is not under attack, then blocks in the canonical chain will be timely, and so finalized blocks will always be timely.
The main case where this may lead to added risk is the case of clients that have high latency but are unaware that they have high latency; they could see timely blocks as non-timely or non-timely blocks as timely. The goal of this mechanism is that if the non-timeliness-dependent fork choice and the timeliness-dependent fork choice disagree, the user should be notified of this, so they would socially verify what is going on; they should not be instructed to blindly accept the timeliness-dependent fork choice as canonical.
Dealing with censorship
We can also use timeliness detectors to automatically detect and block censorship. This is easy: if a block B with self-declared time t is timely, then any chain that does not include that block (either as an ancestor or as an uncle) before time t + (2k+2)\delta is automatically ruled non-canonical. This ensures that a chain that censors blocks for longer than (2k+2)\delta will automatically be rejected by clients.
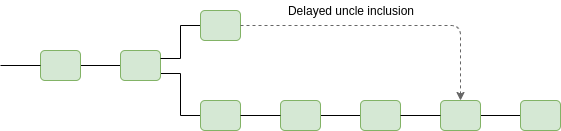
The main benefit of using timeliness detectors here is that it creates consensus on when there is “too much” censorship, avoiding the risk of “edge attacks” that are deliberately designed to appear “sufficiently bad” to some users but not others, thereby causing the community to waste time and energy with arguments about whether or not to fork away the censoring chain (instead, most users would in all cases agree on the correct course of action).
Note that this requires an uncle inclusion mechanism, which eg. eth2 does not have. Additionally, it requires a mechanism by which transactions inside of uncles get executed, so that the censorship resistance extends to transactions and not just the raw bodies of blocks. This requires care to work well with stateless clients.
One additional nitpick is that care is required to handle the possibility of many blocks being published and gaining timeliness status and needing to be included as uncles at the same time. This could happen either due to delayed publication or due to a single proposer maliciously publishing many blocks in the same slot. The former can be dealt with via a modified rule that blocks must include either all timely blocks that are older than (2k+2)\delta or the maximum allowed number (eg. 4) of uncles. The latter can be dealt with with a rule that if one block from a particular slot is included, all other blocks from that slot can be validly ignored.
Note that in the Casper CBC framework, censorship prevention and de-prioritization of chains containing non-timely or censoring blocks by itself suffices to provide the same finality guarantees as we saw for the FFG framework above.
Challenges / todos
- (Non-technical) Come up with the best way to explain to users what happened in the event that timeliness-aware and non-timeliness-aware fork choice rules disagree, and how they should respond to the situation.
- Analyze the behavior of the system in cases where latency is sometimes above \delta, or latency is always potentially above \delta but we have assumptions that eg. some fixed fraction of attesters is honest, or other hybrid assumptions. See if there are ways to modify the rules to improve performance in those scenarios.
- Analyze ways to achieve these properties without including a new class of attestation; instead, reuse existing attestations (eg. the attestations that validators make every epoch in FFG)
- Determine if there are small modifications to “simple” longest-chain-based fork choice rules that allow them to benefit from timeliness detectors to gain a kind of finality.