Timing games in Proof-of-Stake

barnabe · October 20, 2022, 2:17pm

Many thanks to @fradamt for ideas and review on the candidate model, and to Philipp Zahn for discussions on a related problem.

Summary: In Proof-of-Stake, validators lock up stake and are expected to perform duties to maintain consensus. Unlike Proof-of-Work, these duties rely on a schedule, where validators know (typically some time in advance) that they will be expected to do something at some instant t. While the protocol specifies the exact time when the duty is expected to be completed, it remains up to the validator to follow the schedule or not.

We’ve found it difficult to formalise strategic incentives to follow the schedule adequately, and observe the existence of weak incentives to deviate from it: roughly, being late affords a validator either more precise information or larger economic value, but being too late risks being made irrelevant by the other consensus participants.

The finer details of the protocol likely do not matter much in the game, so we build a model additively.

The first model is a “general model”, which introduces the broad strokes of the game. It lacks specification to make it amenable to analysis, but contains some of the features we expand on later.
The second model, “candidate representative game”, is what we would like to analyse. It does not fully model the protocol but it should model just enough to make the game relevant and solvable.
For completeness, we propose a model of the protocol in the third section. We expect this model to not be very useful until more clarity is achieved on the candidate representative game. Once the candidate representative game is well-understood, the idea would be to add features progressively until the protocol is more faithfully modelled. See also my slides presented at the SMGT workshop.

General model

We have a sequence of players drawn randomly from some (finite) set \mathcal{N}.

The game proceeds in rounds indexed by i. Each round has duration \Delta, and the game ends after round K. Assume \mathcal{N} = \{1, \dots, K\}. Let t_i = i \cdot \Delta denote the start time of round i.

Player P_i chooses an action a_i \in A_i, and decides some time t^i \in \mathbb{R}_{>0} when to play the action. After t^i, all players are informed about the action a_i. In particular, the game is played continuously, i.e., strategies may depend on everything that has been observed up to the revealing time t^i.

Ultimately, the payoff function is

U^i(a_i, t^i, a_{-i}, t^{-i}) = \Big( u^i(a_i, a_{-i}) + \mu_i \cdot (t^i - t^{i-1}) \Big) \cdot \mathbb{1}_{\omega^i(a_i, t^i, a_{-i}, t^{-i})}

Some features of the model:

Although we specify a round duration \Delta, nothing prevents players from playing early or late. Ideally, at equilibrium, players play at or close to their round time t_i.
There is a reward term that only depends on the players’ actions, u^i(a_i, a_{-i}).
The longer players wait to release their action after the previous player released theirs, the higher their payoff, with \mu_i \geq 0 for all i.
The payoff is conditional on the realisation of some event \omega^i.

Candidate representative game

We can make the game above more expressive to explore the timing issue in the protocol. We have a finite set \mathcal{N} of validators. Each round i, a proposer and a set of attesters are selected randomly (without replacement for the set of attesters). We can assume that the schedule is known in advance by all validators.

We divide each round in two periods, each of length \Delta, so the duration of a round is 2\Delta. Let t_i = i \cdot 2\Delta be the start of round i and t_{i+1/2} = t_i + \Delta.

In round i, denote P_i \in \mathcal{N} the proposer and \mathcal{A}_i \subset \mathcal{N} the set of attesters, with A_i^j \in \mathcal{A}_i the j-th attester in the set.

Proposers receive a private signal \phi_i \in \Phi and choose when to reveal it. We denote t^i the release time of the proposer assigned to round i. There is a null signal \phi_0 \in \Phi that is known by all players. All signals (those received by players and the null signal) are assumed to be distinct. Signals are meant to represent blocks.

Attesters cast a vote, with attester j assigned in round i casting vote v_i^j \in \Phi. Attesters decide on the timing of their vote release t^j_i. Let v denote the set of all votes, v = \{ v_i^j \}_{i,j}, and v_i all the votes from attesters of round i.

We let N_i(v_i) = |\{ j \in \mathcal{A}_i; v_i^j = \phi_i \}|, i.e., N_i(v_i) is the number of votes obtained by the block at round i. Let \bar{N}_i(v_i) = |\mathcal{A}_i| - N_i(v_i) be the number of votes not obtained by the block at round i.

Proposers have the utility function:

U^P(t^i, t^{-i}, v_i) = \cases{\gamma + \mu \cdot (t^i - t^{i-1}) \text{ if } N_i(v_i) \geq \bar{N}_i(v_i) \\ 0 \text{ otherwise}}

In other words, if the block was voted in by a majority of voters of that round, it eventually makes it into the canonical chain, and the proposer earns the block reward \gamma as well as an additional payoff based on how much time elapsed between their action and the action of the previous proposer (think of \mu as the additional MEV that a proposer can pick up per unit of time).

For a given round i, attesters have the utility function:

U^A(t_i^j, v_i^j, v_i^{-j}) = \cases{ \alpha \text{ if } v_i^j \text{ is correct} \Leftrightarrow |\{ j' \in \mathcal{A}_i; v_i^{j'} = v_i^j \}| \geq |\mathcal{A}_i| / 2 \\ \quad \quad \text{and fresh } \Leftrightarrow t_i^j \leq t^{i+1} \\ \\ 0 \text{ otherwise}}

In other words the attester realises a positive payoff if:

Correctness: They vote as the majority of attesters in their round does
Freshness: They publish their vote before the next proposer (at round i+1) releases their block

Some features that are missing:

In reality, there is an unbounded amount of rounds
There is also network latency: players learn about other players’ actions after some random delay \delta (delays could be i.i.d or player/round-specific). As a simpler question, one could use a fixed \delta latency for everybody
In the proposer payoff function, the time-based reward should depend on the latest valid block rather than the latest block. Define

\hat{i}(v) = \max_k \{ k \in \{1, \dots, i-1 \}; N_k(v_k) \geq \bar{N}_k(v_k) \}

then \hat{i}(v) is the latest block preceding the block at round i, that was voted in by attesters. We drop the dependence on the attester votes to give the proposer payoff:

U^P(t^i, t^{-i}, v_i) = \cases{\gamma + \mu \cdot (t^i - t^{\hat{i}}) \text{ if } N_i(v_i) \geq \bar{N}_i(v_i) \\ 0 \text{ otherwise}}

Expected results

We foresee the existence of two equilibria:

In the first (ideal) equilibrium, players are honest and complete their duties during their assigned rounds (for proposers, in the first half of the round; for attesters, in the second half of the round). Given the absence of latency in our candidate representative model, we expect the equilibrium would see players doing their actions as late as possible, yet within their round.
In the second (bad) equilibrium, all players just delay their actions indefinitely. It is not even clear that we can speak of an equilibrium, more like a sequence of best responses that always increases the delay within which the players complete their duties.

Difficulties

The game is dynamic and we want to express the fact that players are continuously playing and updating their view of the game state based on other player actions. We fail to find an equilibrium notion that is tractable in this setting.

Opportunities

Given an appropriate model and a description of its equilibria, we expect it would be easier for us to (mechanism) design our way out of the bad dynamics.

LMD-GHOST protocol

The protocol is specified as follows. We provide it here for completeness, even though it is clear that some parts can be abstracted away, as in the previous candidate representative model.

We have a directed tree \mathcal{G}_t, such that \mathcal{G}_t \subseteq \mathcal{G}_{t'} for t \leq t' (the graph grows over time). Vertices of the graph are called blocks. We have \mathcal{G}_0 = (\{ B_{-1} \}, \{\}), where B_{-1} is the genesis block, known by all players. We use \mathcal{G}_i = \mathcal{G}_{t_i} for simplicity.

At t_i, proposer P_i, having observed \mathcal{G}_i and all votes from past attesters (to be defined below), chooses B_p \in \mathcal{G}_i (a parent block) and creates a new block B_i with a single directed edge from B_p to B_i.
At t_{i+1/2}, attesters from \mathcal{A}_i, having observed \mathcal{G}_{i+1/2}, each produce a vote v_i^j for the head block of \mathcal{G}_{i+1/2}.
The head block B_h is given by the GHOST fork choice rule:
- Let \text{children}(B) denote the set of children blocks of some block B and \text{desc}(B) all descendents of B, including B itself.
- Let v(B) denote the direct weight of B, i.e.,
v(B) = |\{ (i, j) \in \mathbb{N} \times \mathcal{N}; j \in \mathcal{A_i}, v_i^j = B \}|
- Let w(B) denote the weight of B, defined by
w(B) = \sum_{B' \in \text{desc}(B)} v(B')
- Given \mathcal{G_t}, start from B^0 = B_{-1} (“the block at height 0”)
- Choose B^{i+1} = \text{argmax}_{B \in \text{children}(B^i)} w(B) until \text{children}(B^i) = \emptyset
- Let B_h denote the leaf block where the loop stops. For any graph \mathcal{G}_t, we can always obtain the head block. The canonical chain is the unique chain of blocks starting from B_h and ending at B_{-1}.

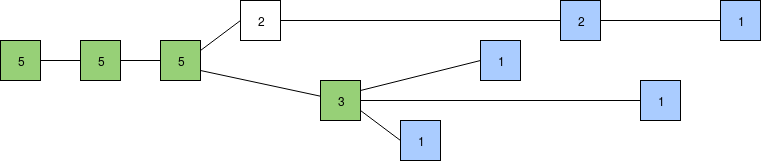
An example of LMD-GHOST. Blocks in blue have direct weight = 1 while other blocks have direct weight = 0. The number in the block is the weight w(\cdot). For instance, the block denoted 3 inherits 3 units of weight from its descendants, and the left-most inherits 5 units of weight from its descendants. There is currently a tie for the head of the chain between the three blocks with weight 1 in the bottom branch (the children of block 3). We can use an arbitrary tie-breaking rule in that case.

At t_{i+1}, proposer P_{i+1} includes in their block a set of votes \mathcal{V}_{i+1}.

After some time has passed, say K rounds, the game stops and players receive the following payoffs:

If B_i is included in the canonical chain, proposer P_i receives \gamma per fresh and correct vote v included in \mathcal{V}_i
- A vote v included in block B_i is fresh if it was published by an attester from \mathcal{A}_{i-1}
- A vote v included in block B_i is correct if \text{parent}(B_i) = v
In addition to the above payoff, the proposer P_i receives \mu \cdot (t_i - t_{i-1}) for some \mu > 0. This corresponds to the economic value of the block, i.e., the proposer that waits longer can include more valuable transactions in their block.
If vote v_i^j is fresh (i.e., included in B_{i+1}), correct (i.e., \text{parent}(B_i) = v_i^j), and B_i is included in the canonical chain, attester j receives payoff \alpha

This is the “honest” protocol, but a proposer has the incentive to propose their block as late as possible to maximise \mu \cdot (t^i - t^{i-1}) (we use superscript to denote that the proposer has control over their proposal time t^i, but in the honest protocol, t_i = t^i). On the other hand, a proposer who proposes their block very late risks not making it into the canonical chain.

Attesters also want to send their votes early enough that it can be picked up by the next proposer, so that their vote is fresh, but they also want to be correct. Hence if they expect the proposer of their round to be late, they may want to wait some time before sending their vote.