Adding some napkin math to clarify things further:
Semantic chunking lets validators start executing after the first chunk arrives instead of waiting for the full block. We assume the following parameters:
- 150M gas limit → chunk cap 2^{24} → 9 chunks
- 1 s execution per block → exec/chunk e = E/k \approx 0.111 s (111 ms)
- 50/25 Mbit/s down/up links (5.960 MiB/s, 2.980 MiB/s)
- 2 MiB payloads
Also check out this simulation tool, allowing you to compare propagation-to-execute delays for big monolithic blocks vs multiple smaller ones.
Quick Math
The following is a rough estimate based on a few strong assumptions. It gets the point across, but take the numbers with a grain of salt.
First, we’re still ignoring networking hops and only look at the download:
-
Full download (2 MiB):
D = \frac{2}{5.960} \approx 0.3356 s -
Per-chunk size: s_c = \frac{2}{9} \approx 0.222 MiB
- Per-chunk download: d_0 = \frac{s_c}{5.960} \approx 0.0373 s
- Per-chunk upload: \frac{s_c}{2.980} \approx 0.0746 s
-
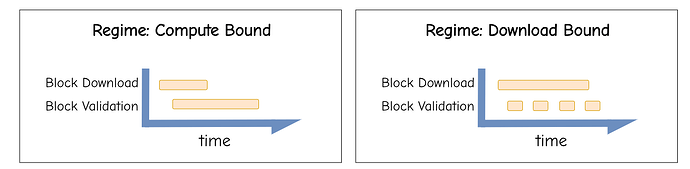
Regime: compute-bound 111 ms exec ≫ 37 ms download
Latencies
- Monolithic: T_{\text{mono}} = D + E \approx 0.3356 + 1.0000 = 1.3356 s
- Chunked (streaming): T_{\text{chunk}} = d_0 + E \approx 0.0373 + 1.0000 = 1.0373 s
- Gain: ~0.298 s per block
Why: Streaming hides all later downloads under execution/validation; only the first chunk’s transfer remains on the critical path.
Multi-Hop Store-and-Forward Simulation
Model: Each hop performs download then upload (store-and-forward).
- Monolithic must forward the entire 2 MiB every hop, then execute.
- Chunked forwards first chunk through the hops, starts execution, and overlaps the rest under execution (compute-bound).
Closed Forms
- Per-hop payload time (monolithic):
\frac{2}{5.960} + \frac{2}{2.980} \approx 0.3356 + 0.6711 = 1.0066 s
\Rightarrow T_{\text{mono}}(H) = 1 + 1.0066 \times H - First-chunk per-hop time (chunked):
\frac{2/9}{5.960} + \frac{2/9}{2.980} \approx 0.0373 + 0.0746 = 0.1118 s
Inter-arrival at destination = \frac{2/9}{2.980} \approx 0.0746 s; since e=0.111 \ge 0.0746 ⇒ compute-bound
\Rightarrow T_{\text{chunk}}(H) = 1 + 0.1118 \times H
Results
| Hops | Monolithic (s) | Chunked (s) | Gain (s) |
|---|---|---|---|
| 1 | 2.0066 | 1.1118 | 0.8948 |
| 2 | 3.0133 | 1.2236 | 1.7896 |
| 4 | 5.0265 | 1.4472 | 3.5793 |
| 6 | 7.0398 | 1.6711 | 5.3690 |
| 8 | 9.0531 | 1.8948 | 7.1586 |
Why it scales with H: Monolithic pays full store-and-forward per hop; chunking puts only the first chunk’s store-and-forward on the critical path and overlaps everything else under execution.
Simulation Code
# Params
MiB = 1024**2
down_Mbps, up_Mbps = 50_000_000, 25_000_000
down_MiBs = (down_Mbps/8) / MiB # ≈ 5.960 MiB/s
up_MiBs = (up_Mbps/8) / MiB # ≈ 2.980 MiB/s
S_exec = 2.0 # MiB on critical path
E, k = 1.0, 9
e = E / k # 0.111 s/chunk
s_c = S_exec / k # 0.222 MiB/chunk
def mono(H):
return E + H * (S_exec/down_MiBs + S_exec/up_MiBs)
def chunked(H):
first = H * (s_c/down_MiBs + s_c/up_MiBs)
inter = s_c / up_MiBs
if e >= inter: # compute-bound
return first + E
else:
return first + (k-1)*inter + e
for H in [1,2,4,6,8]:
print(H, round(mono(H),4), round(chunked(H),4),
round(mono(H)-chunked(H),4))