We are building a competing sharded blockchain, and are researching ways to enable fast cross-shard transactions.
In this post I assume that the cross-shard txs are executed as a series of single-shard execution steps, with some sort of proof that the previous steps were properly executed (or Receipt) passing from one shard to another between steps.
Excluding from the discussion delayed state changes, the receiving shard needs to be reasonably certain that the transaction actually has happened and its result will not be reversed (due to forks for example).
The present Ethereum Sharding design (or at least my understanding of it) assumes that the validators in each shard have very little responsibility, and the finality only comes from the beacon chain and casper.
In our sharding design we use a special continuous consensus algorithm (we call it TxFlow) that is more complicated than just proposers emitting blocks every 8 seconds, with a following attestation and notarization. The main issue we are trying to address is how to make it possible for a cross-shard transaction to be rerouted to another shard (i.e. how to get a reasonable certainty that a transaction was properly applied to the state, and it won’t get reversed) without a synchronization with the beacon chain.
Since we want to avoid forks after the block is published, the algorithm we run needs to have the byzantine consensus guarantees. At the end of the post I will also touch on the implications of the fact that we can’t expect a shard to have less than 1/3 malicious validators – which at this point is the main active area of research.
Informal spec of TxFlow
The messages DAG
In TxFlow all the participants assigned to a single shard (we call them validators) participate in building a DAG of messages. Validators collect transactions targeted for this shard. Occasionally each validator creates a message that includes all the new transactions this validator has accumulated and hashes of messages from other validators. Validator then sends it to a few peers in this shard. If their peer haven’t seen some of the messages this validator referenced, they fetch them. In result defining a gossip protocol for messages DAG
We define message A directly approving another message B if message A contains hash of message B. Then A indirectly approves B if there is a path between these two messages. For simplicity we say “approves” to mean “directly or indirectly approves”.
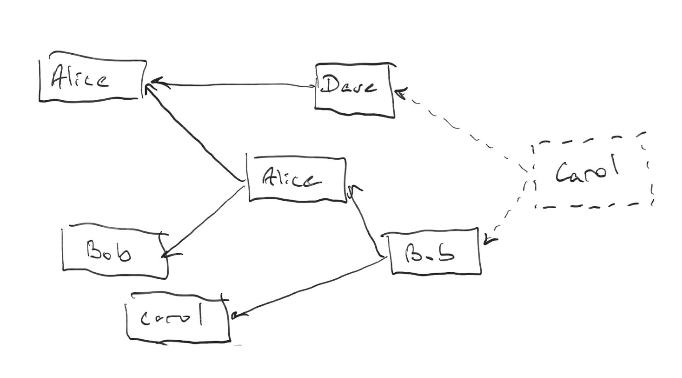
When a validator posts a message, they choose all the messages known to them (including their own) for which they do not know any other message approving them. E.g. consider the following messages DAG:
When Carol posts her new message, she approves messages from Dave and Bob, for which she knows no other message approving them. She doesn’t approve her own previous message since she knows that it is already approved by a message from Bob.
Epochs
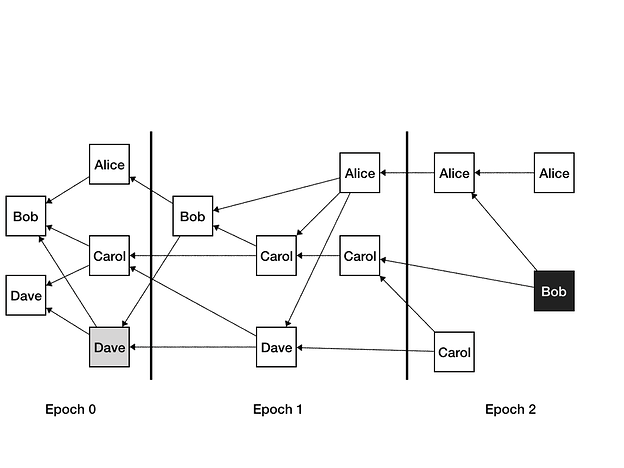
Each message has an epoch assigned to it. Here’s an example of a message DAG with epochs assigned:
A message M is assigned an epoch E, if it directly or indirectly approves messages with epoch E-1 from more than ⅔ of participants. In the picture above there are four participants. The gray message from Dave still has epoch 0, because it only approves messages from two validators (Bob and himself) with epoch 0, which is less than ⅔ of four participants. His very next message has epoch 1 because it now also approves an epoch 0 message from Carol, bringing the total number of validators with epoch 0 messages it approves to 3.
Similarly, the black message from Bob approves messages with epoch 1 from three validators: Carol, Alice and himself, which is more than ⅔ of all the validators, and thus the epoch of the message is 2.
For simplicity, it is also desirable that each validator has a message in each epoch. With the definition above a validator might skip an epoch. For example, consider the message from Alice in epoch 1. It approves three messages in epoch 1, and thus shall be in epoch 2, which would result in Alice never having a message in epoch 1. To make sure that each validator has a message in each epoch, we change the epoch computation rule to be the minimum of the computed epoch, and last epoch from the validator plus 1. If this rule kicks in, the validator is encouraged to post a chain of multiple messages with all the epochs that are being skipped, like on the picture above Alice has immediately posted a message in Epoch 2 approving the message in Epoch 1 for which the rule was applied.
Leaders
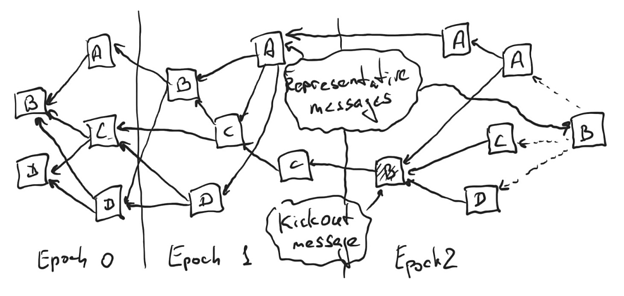
We assign one validator to each epoch except for Epoch 0. Let’s say that Alice is assigned to Epoch 1, Bob is assigned to Epoch 2, Carol is assigned to Epoch 3 and Dave is assigned to Epoch 4. We call such an assigned validator a Leader. Whenever a Leader assigned to a particular epoch publishes a message with that epoch for the first time, such a message is called a representative message for epoch X, and a block for epoch X is published. All the transactions in all the messages approved by the representative message for epoch X but not reachable from any representative message from lower epochs are included into such block. The representative message also contains a BLS signature part from the Leader.
Whenever any other validator approves (directly or indirectly) a representative message, they post their part of the BLS multisignature. Such a message is called an Endorsement. For simplicity of terminology we assume the representative message to be an endorsement of itself. By the time more than ⅔ of the validators approved a representative message (and correspondingly a block), we have more than ⅔ of validators endorsing and signing it. Such a block can be routed to other shards to perform actions that depended on the finality of transactions included in the block.
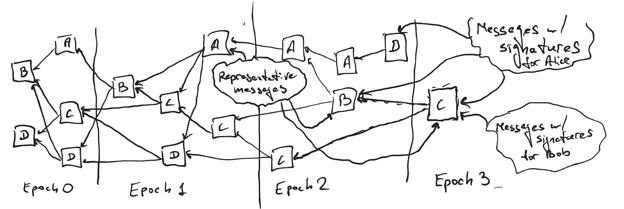
Consider the DAG above. Alice is assigned epoch 1, Bob epoch 2 and Carol epoch 3. The first message from Alice in Epoch 1 is her representative message. Once Bob, Dave, and Carol each first publish a message that directly or indirectly approves it, they each include a BLS signature part. Both representative messages and messages with signatures (endorsements) are shown in the picture.
The block is published once it has been endorsed by more than ⅔ of all the validators. Thus, on the picture above, Alice’s block was published once 3 out of 4 endorsements were published (including Alice’s itself, e.g. the block might have been published once Dave and Bob published their endorsements in Epoch 2), and Bob’s and Carol’s blocks are not published yet, because they have 2 and 1 endorsements respectively (including the parts from the Leaders themselves).
Skipping blocks
There’s one last issue to be addressed. What if a Leader of a particular epoch is offline, or intentionally delays a block? Or what happens if a block for epoch X gets published before the block for epoch X-1 (which is possible)?
We address it in the following way: first, we modify a condition under which a message is considered to be an endorsement (and thus contains a signature for the block). A validator V only endorses and signs a block for epoch X in the message M that they post if:
- M approves a representative message for epoch X;
- No other message posted by V previously approves the representative message for epoch X; and
- No other message posted by V previously approves representative message for any epoch higher than X.
While we do not prove it here explicitly, with the addition in bold it is impossible for a block for epoch X-1 to be published after a block for epoch X. Note that it is OK if M itself approves multiple representative messages (for example on the image above Carol’s message in Epoch 3 would still endorse and provide signatures for both Alice’s and Bob’s representative messages), the message approving a representative message is only not considered an endorsement (and thus the signature is skipped) if some previous message from the same validator approved representative message from a later epoch, like on this picture:
This approach works great in simple cases, and with a small modification works for a general case. First, let’s consider the simple cases:
- A block for epoch X-1 was published, a representative message for epoch X was posted, and more than ⅔ of validators have endorsed it. In this simple case block X gets published, and the system continues its operation to work on further blocks.
- A block for epoch X-1 was published, a representative message for epoch X was not seen yet, a representative message for epoch X+1 was published, and more than ⅔ of validators have endorsed it. In this case (assuming less than ⅓ of validators are malicious) the representative message for epoch X will never get more than ⅔ validators endorsing it, since among the more than ⅔ of validators who endorsed the representative message for X+1 no honest validator now can endorse the representative message for X (it follows from the addition in bold above to the condition under which a message is considered to be an endorsement). Thus the block for the epoch X+1 can be posted without a fear that the block for epoch X will ever be posted in the future (and thus the block for epoch X is skipped).
Now let’s consider the following case:
- A block for epoch X-1 was published, a representative message for X was posted and has ⅔-1 endorsements, a representative message for X+1 was posted and has ⅔+1 endorsements.
In this case, there could be three possible situations:
- Unknown to the observer, there are two other validators who already signed the representative message for X, and have already published the block for epoch X;
- Unknown to the observer, each other validator has already signed the block X+1, and thus will never sign block X, and the block X+1 was already published;
- All the validators who signed neither X nor X+1 (there are fewer than ⅓ such validators) are malicious or offline and will never post any further message.
No validator can publish block X+1 yet, because block X might have been published concurrently due to (1). No validator can publish block X because it doesn’t have more than ⅔ signatures. No validator can wait for further information since due to (3) it could be that no more information will ever be available.
To address it, we add two final modifications to TxFlow.
First, whenever a Leader for epoch X+1 publishes their representative message, if such message directly or indirectly approves the representative message for X, then whenever block X+1 gets published, block X also gets published even if it doesn’t have more than ⅔ of endorsements.
Second, if by the time the Leader of epoch X+1 is ready to publish their representative message they have not seen yet the representative message for X yet, they post a special kind of a message on the DAG calling other validators to promise not to endorse X (or any other representative message with smaller epoch that is not approved by representative message of epoch X+1) should it appear in the future. We call such a message a kickout message. If another validator posts a message that approves a kickout message for block X, but doesn’t endorse the representative message for epoch X itself, no future message from such validator will be considered to be an endorsement for epoch X, even if such message approves the representative message for epoch X. If a validator posts a message that for the first time approves a kickout message for block X, but also approves the block X itself, it is still considered to be an endorsement of X.
Once the kickout message collects more than ⅔ of approvals, the Leader of epoch X+1 posts their representative message approving all the approvals of the kickout message. If any approval of the kickout message also endorsed X, it naturally creates an indirect approval from X+1 to X, and thus both blocks get published. Otherwise, there are more than ⅔ of validators that can’t sign X any longer (unless they are behaving maliciously), and thus X+1 can be safely published.
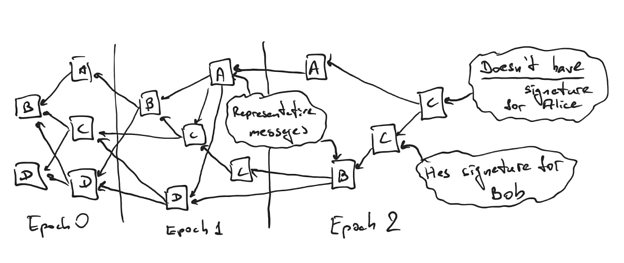
Consider the DAG above. Alice published her representative message, which Bob missed, so Bob publishes a kickout message to collect promises not to sign Alice’s epoch block. Alice approves such message but the same message also approves her representative message. Carol and Dave just approve the kickout message, but not the Alice’s representative message. If the rightmost message from Bob (which will be his representative message) approves Carol’s and Dave’s message but not Alice’s, then Alice’s epoch block is kicked out (since Bob, Carol and Dave all promised to not endorse and sign it in the future). If Bob’s message approves Alice’s (and optionally Dave’s and/or Carol’s), then Alice’s block gets published together with Bob’s once Bob accumulates more than ⅔ endorsements on his representative message.
This approach has a certain liveness issue (while a Leader for X is collecting the promises to exclude X-1, the leader for X+1 won’t see their representative message and can start collecting the promises to exclude X), which we do not directly address in this write-up.
Transactions execution and validation
The protocol as described above only reaches the consensus on the order of blocks (and thus transactions), not on the new state.
Transactions cannot be executed or validated until the order is defined, so no transaction can be executed before the epoch block is known.
To address this, we split the endorsement and the signature: the validator first posts a message with an endorsement (with all the rules as to what is considered an endorsement discussed above), then starts validating transactions in the block, and once the transactions are validated and executed, posts the second message with a new merkle root for the state and the signature.
Note that it is the first message (the endorsement) that decides the order of blocks. The transactions must always be processed in the order defined by the TxFlow consensus.
A validator V can start validating transactions for epoch X immediately as they see a representative message for epoch X. Even if the leader for X+1 misses the representative message for X, V will post the representative message for X as a response to the kickout message from X+1, and for as long as the leader for X+1 doesn’t try to censor X (in which case it will ignore the message from V), the epoch block for epoch X will be posted. Note that the leader for X+1 can only censor the epoch block from X if more than ⅔ of validators missed the representative message from X. Otherwise, it won’t be able to collect a sufficient number of promises to skip X.
An epoch block is signed and sent over to other shards once more than ⅔ of the validators validated and executed all the transactions and posted their signatures with the merkle tips. Naturally, the merkle tips from all the validators will match, as long as no validator is behaving maliciously.
Why all this complexity?
Up until this moment, it might appear to be an overly complex version of what Ethereum does with proposers and attesters, but the extra complexity helps get around the problems discussed above.
Most importantly, for as long as less than ⅓ of validators in each shard are malicious, forks are impossible. If validators are rotated rather often, and the adaptive adversary cannot corrupt them sufficiently quickly, this provides a meaningful means of finality. Cross-shard transactions can be routed to other shards after a block for each epoch is published.
Secondly, all the misbehavior is recorded in the DAG, so attempting to create forks, censor blocks or deviate from the protocol in any other way is persisted to simplify detecting and slashing. In particular, if validators are rotated one by one, even if a cross-link to the beacon chain skips most recent blocks, the validators will continue building the messages DAG on top of those skipped blocks (technically TxFlow is not required for this, and likely in Ethereum proposed sharding a similar technique is used).
Finally, TxFlow removes the dependency on the real world time. Ethereum today depends on clocks being synchronized up to a few seconds, achieving which is a very hard task in a decentralized system. 8 seconds block time in Ethereum is also rather arbitrary, while with TxFlow the time between blocks is close to the minimum time needed for a byzantine majority of validators to acknowledge the block creation.
How final is the finality?
Above we claimed that unless ⅓ of the validators in a single shard are malicious, the block is irreversible. Even if an adaptive adversary attempts to corrupt the validators, for as long as they don’t corrupt ⅓ of them before a cross-link was created, the block is not reversible.
There’s a widely believed trilemma that a blockchain protocol can’t be simultaneously scalable, decentralized and secure. The sharding designs of both Ethereum and NEAR Protocol are scalable and decentralized, and thus will have certain challenges to address with security.
In particular, with a large number of shards s (say hundreds or thousands) each shard only has 1/s validators. An adversary controlling a large percentage of a total stake in the system (say 30%) is expected to have a byzantine majority (more than ⅓) of validators in one shard with a non-trivial chance.
Clearly, such an adversary can stall a shard by not signing any messages. Stalling a shard is undesirable, but doesn’t compromise the security per se.
Let’s observe that if an adversary controls more than ⅓ of the validators, they have a practical way of actually compromising the security by producing a double spend. All they need is to create two conflicting representative messages in one of the epochs in which they are a leader and send one of the messages to half of the remaining validators, and another to the remaining half for endorsements and signatures. If they are lucky and those signatures are produced before the two halves of the validators figure out the conflicting messages were created, the ⅓+ malicious validators sign both messages, effectively getting two representative messages for that epoch with more than ⅔ signatures. Such two messages might include a transaction that sends money from the same account to two different accounts on two different shards, and the two produced blocks will be routed to those two shards.
An adversary controlling more than ⅔ of the validators can create any blocks, fabricate any state changes, and arbitrarily fork the chain of the epoch blocks.
Both forks and fabricated state changes can be challenged and slashed if they are detected in time. If an adversary controls less than ⅔ of the validators, a malicious attempt to fork the epochs blockchain is likely to be noticed during the TxFlow communication while the transactions are being validated. Figuring out exact guarantees here is the most interesting open question at this point.
If an adversary controls more than ⅔ of validators, unless some artificial delays are introduced, the adversary can propose and pretend to validate with practically no network or CPU overhead, and thus can compromise the system.
To that end we observe that if an adversary controls less than ⅓ of the total stakes in the system with N validators, and there are K shards with N/K validators in each, the chance that the adversary controls more than ⅔ of the validators in any shard is negligibly small for most reasonable values for N and K. Some values are presented below (zero indicates a chance less than 10e-15):
| n | k | n/k | % |
|---|---|---|---|
| 500 | 5 | 100 | 6.00E-15 |
| 500 | 2 | 250 | 0 |
| 1000 | 10 | 100 | 3.50E-13 |
| 1000 | 4 | 250 | 0 |
| 10000 | 100 | 100 | 4.98E-12 |
| 10000 | 40 | 250 | 0 |
| 10000 | 10 | 1000 | 0 |
| 100000 | 1000 | 100 | 6.29E-12 |
| 100000 | 400 | 250 | 0 |
| 100000 | 100 | 1000 | 0 |
| 1000000 | 10000 | 100 | 6.44E-12 |
| 1000000 | 4000 | 250 | 0 |
| 1000000 | 1000 | 1000 | 0 |
So for as long as the validators are sampled randomly, and rotated sufficiently often so that an adversary can’t corrupt them adaptively fast enough, the honest validators have time to challenge the adversary attempting to fork the chain or to fabricate the state.
Discussion
As I mentioned above, some values of TxFlow are 1) removing the dependency on the real clock; 2) reduced forkfulness and 3) finality of epoch blocks under an assumption of fewer than 1/3 of validators in the shard are malicious (and probably a reasonable approach to detect and prevent malicious behavior as long as the number of adversaries in a shard is less than 2/3).
Importantly, the number of communications per block is pretty small, unlike with most other BFT algorithms available (the faster consensus per epoch block comes from the fact that consensus on each epoch block can fail to be reached at all – if the leader misses their block).
For us the most interesting value is the last one (finality without communication to the beacon chain under certain assumptions), since for the cross-shard transactions getting to a state where shards can finalize blocks without cross-linking to the beacon chain could be very desirable.
Would love the input of the community on the algorithm and its applications.
 , I think reputation is a very underexplored topic in crypto in general.
, I think reputation is a very underexplored topic in crypto in general.