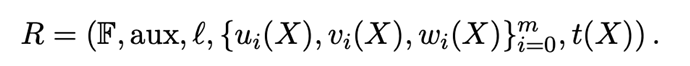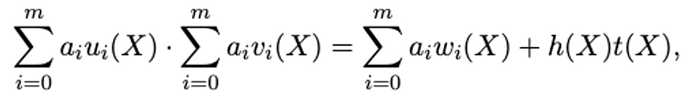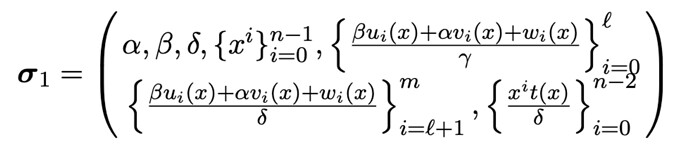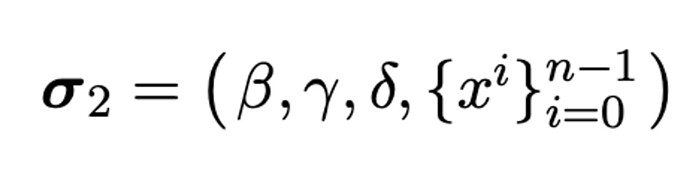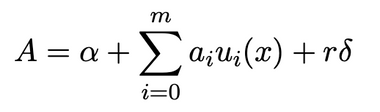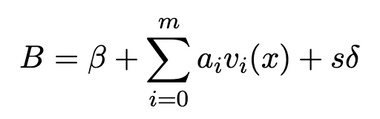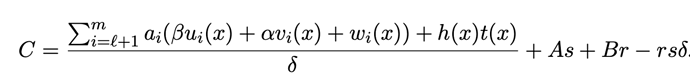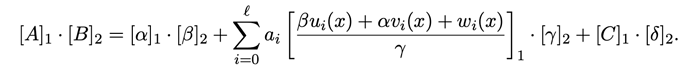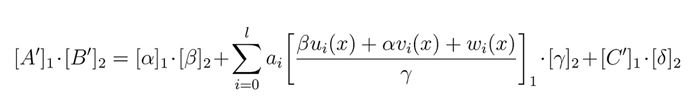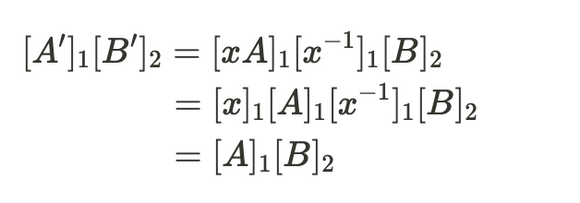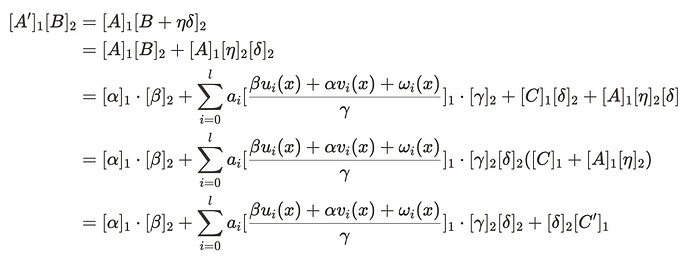1. Transaction Malleability Attack
In 2014, MT.GOX exchange claimed to have suffered from a transaction malleability attack on Bitcoin, resulting in a loss of approximately 850,000 BTCs. The attack proceeded as follows: The attacker initiated a withdrawal transaction A on MT.GOX and then manipulated the transaction signature before transaction A was confirmed. By altering the signature, which is used to identify the uniqueness of a transaction’s hash, the attacker generated a forged transaction B. If transaction B was included in the Bitcoin ledger by miners before transaction A, subsequent miners packaging transaction A would see it as a double-spending issue, as transaction B had already used the same unspent transaction output (UTXO). As a result, they would refuse to include transaction A. Finally, the attacker would file a complaint with the exchange, claiming non-receipt of funds. The exchange, upon checking the transaction status on the blockchain using transaction A, would find that the withdrawal transaction indeed failed and would proceed to transfer funds to the attacker, resulting in financial loss for the exchange. This type of malleability attack does not alter the content of the transaction itself but only changes the transaction signature.
The transaction malleability attack in Bitcoin is a vulnerability in the Elliptic Curve Digital Signature Algorithm (ECDSA). Bitcoin prevents double-spending attacks caused by transaction replay by verifying whether the transaction ID already exists. The transaction ID is generated from the hash of the transaction content. Therefore, if the transaction signature (sigscript) is modified, the transaction ID will also change. By manipulating the S value in the signature, the attacker can forge another valid signature. However, this attack method cannot alter the transaction inputs and outputs. Bitcoin introduced the Segregated Witness (SegWit) solution in BIP-141, which stores transaction signatures in the witness section instead of the transaction data itself, effectively mitigating this attack and achieving scalability.
This inherent malleability security issue, caused by algorithmic design, is also present in the zk-SNARK algorithm Groth16.
2. Groth16 Algorithm
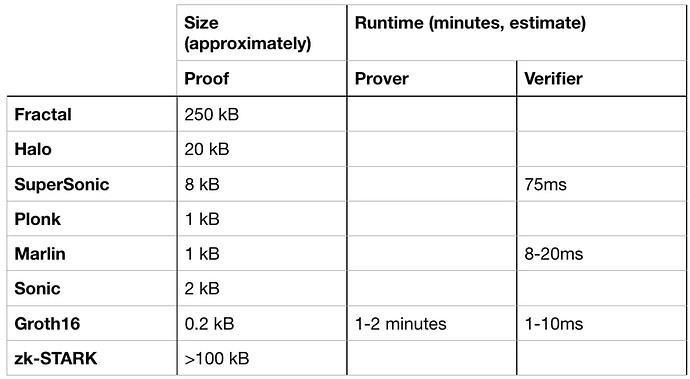
Groth16 algorithm is one of the most widely used non-interactive zero-knowledge proof solutions for zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge). Compared to other zk-SNARKs algorithms, it produces smaller proof sizes and offers faster verification speeds. As a result, it has been applied in projects such as Zcash and Celo. The following diagram lists common zk algorithms:
https://medium.com/coinmonks/comparing-general-purpose-zk-snarks-51ce124c60bd
2.1 Groth16 Algorithm Overview
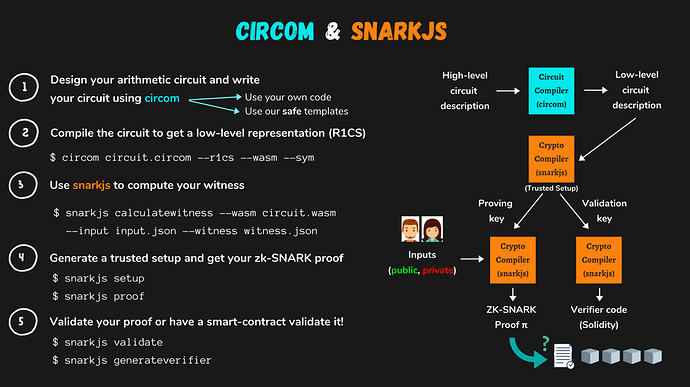
Typically, the development process of a zk-SNARK DApp involves several steps. Firstly, the project abstracts the business logic and translates it into a mathematical expression. Then, this expression is converted into a circuit described in R1CS (Rank-1 Constraint System) format. However, R1CS can only sequentially verify each logical gate in the circuit, which is highly inefficient. Therefore, the zk-SNARKs algorithm transforms it into a QAP (Quadratic Arithmetic Program) circuit. This involves converting the constraints represented as vectors in R1CS into interpolation polynomials. The resulting proof can be verified using off-chain cryptographic libraries or on-chain smart contracts. Finally, the generated proof is validated for its legitimacy using a verification contract based on the circuit.
In the Groth16 algorithm, which is a zk-SNARKs algorithm, it also involves zero-knowledge proof circuits. The constraints of its quadratic arithmetic circuit are as follows:
- Finite Field F: A field containing a finite number of elements that satisfies the following properties:
-
Closure: If any two elements of the finite field a、b\in F_{q},then a+b and a\cdot b also belong to the finite field.
-
Associativity:If any a、b、c\in F_{q},then:
(a+b)+c=a+(b+c)、(a\cdot b)\cdot c = a \cdot(b \cdot c)
-
Commutativity: If any a、b、c\in F_{q},then: a+b=b+a,a \cdot b=b\cdot a
-
- aux: Additional information
- l: Order
- Polynomials u_{i}(X),v_{i}(X),w_{i}(X): Third-party parameters generated in the trusted setup of Groth16 for proof generation.
- Polynomial t(x): R1CS specifies that a circuit must satisfy A(X_{i})\cdot B(X_{i}) = C(X_{i}). For a set of X_{i}\in\{{x_{1},x_{2},...,x_{m}\}}, it holds that a(x_{i})\cdot b(x_{i})=c(x_{i}). However, R1CS requires checking each of the m constraints one by one. In other words, even if R1CS checks the first 9 constraints and they pass, the last constraint could still fail, rendering the entire circuit invalid. This means that every verification must complete all 10 constraints. On the other hand, QAP (Quadratic Arithmetic Programs) transforms this problem into a polynomial problem. If for every X_{i}\in\{{x_{1},x_{2},...,x_{m}\}} the equation holds, it is equivalent to the polynomial t(X)=(X-a_{1})(X-a_{2})\dots (X-a_{m}) being a solution to A(X_{i})\cdot B(X_{i}) -C(X_{i}), which means t(X) divides A(X_{i})\cdot B(X_{i}) -C(X_{i}). This allows all the constraints to be verified at once.
It is important to note that the values computed by the left and right polynomials are equal only when x_{i} \in \{{x_{1},x_{2},...,x_{m}\}}, not when the polynomial equation itself holds. In other words, at other points A(X_{i})\cdot B(X_{i}) -C(X_{i}) \ne 0. Therefore, in practical computations, to obtain more accurate results, usually more than just the m given points are used to generate the polynomial. Hence, the core equation of the Groth16 algorithm is as follows:
The Groth16 algorithm aims to prove that the Prover knows a set of polynomial solutions, i.e., the witness h(x) satisfying the above equation.
2.2 Trusted Setting
Since the Groth16 algorithm performs calculations on elliptic curve fields, where values are represented as coordinate points, how can we represent polynomials using coordinate points? This requires the use of elliptic curve pairings. Here’s a brief example of elliptic curve pairings, but for a more detailed explanation, please refer to Vitalik’s Blog. In a finite cyclic group (a group that can be generated by a single element), if \alpha \ne 0 and b=\alpha \cdot a, we call (a,b) an \alpha pair. Similarly, the point (f(x)G,\alpha f(x)G) is also an \alpha pair, and in practical calculations, this point corresponds to a unique polynomial f(x). In this way, we can represent polynomials using \alpha pair.
Now, let’s assume that there is a set of \alpha pairs (P_{1},Q_{1})、(P_{2},Q_{2})、(P_{3},Q_{3}\dots (P_{n},Q_{n}). To generate a new \alpha pair$(P’,Q’)$, we need to know a set of coefficients k_{1}、k_{2}\dots k_{n} so that P'=k_{1}P_{1}+k_{2}P_{2}+...+k_{n}P_{n},Q'=k_{1}Q_{1}+k_{2}Q_{2}+...+k_{n}Q_{n}
Since simple pairings are not suitable for cryptography, a trusted setup will first select a set of random numbers \alpha,\beta,\gamma,\delta,x, and compute a set of polynomials implicitly containing pairs with$\alpha,\beta,\gamma,\delta$,Ultimately, a Common Reference String (CRS) σ is generated, which is divided into two parts, σ1 and σ2, for the Prover and Verifier to use. The specific calculations are as follows:
2.3 Prover Proof Generation
The generation and verification of proofs in Groth16 are closely related to bilinear pairings. Bilinear pairings are a method for proving the correctness of elliptic curve pairings without revealing the coefficients. The bilinear pairings used in Groth16 involve three elliptic curve groups: G_{1}, G_{2}, G_{T}. The elliptic curve equations for these three groups are all of the form: y^{2}=x^{3}+ax+b. However, G_{2} are defined over an extension field of G_{1}, and satisfy the mapping e:G_{1}\times G_{2}\rightarrow G_{T}. The specific properties are as follows.
Suppose that for arbitrary \alpha P\in G_{1},\beta Q \in G_{2}:
The above equation represents that, under the condition of satisfying the bilinear mapping, the coefficients can be extracted separately. Therefore, assuming we need to verify if the point $(P,Q)$in G1 is an \alpha pair, we only need to know one alpha pair (W,\alpha W) in G2, and we can verify if point P is an \alpha pair using the following equation.
The pairings used in the Groth16 algorithm are more complex and involve multiple pairings, which will not be further discussed in this article. In summary, the Prover calculates the quotient h(x) based on the chosen random numbers r and s, and uses the public string σ1 generated from the trusted setup to generate the corresponding Proof π = ([A]1,[C]1,[B]2) through bilinear pairings. The specific calculation process is as follows:
The proof generated is as follows:
2.4 Verifier Proof
According to the bilinear pairing used in Groth16, the Verifier validates the following equation after receiving the proof \pi[A, B, C]. If the equation holds true, it indicates a successful proof verification.
In the actual project verification process, there is a third parameter called public_inputs. This parameter represents a set of inputs to the circuit known as the “statement”. Prover and Verifier need to reach a consensus on the data being computed and verified, i.e., which specific set of actual data is used to generate the proof and perform the verification.
3. Groth16 Algorithm Melleability Attack
Since the verification equation passes the verification as long as the left and right equations are equal, A, B and C in the proof can be falsified as A’, B’ and C’:
Here, [A']_{1} represents a proof A' in G_{1}, and similarly, [B']_{2} represents the corresponding proof B' in G2. Depending on the computational equation, there are two ways to forge the proofs as follows.
3.1 Multiplicative Inverse Construction
The multiplicative inverse refers to the property that for any element a in group Q. There exists another element b in Q so that the following equation holds:
Here, e refers to the identity element, which has a value of 1 in the real number field. Let’s provide a simple example to illustrate the multiplicative inverse. In the usual real number field, the multiplicative inverse of 3 is \frac{1}{3}. In the Groth16 algorithm, let’s assume we select a random number x in the finite field G1 and compute its inverse x^{-1}, then forge the corresponding proof A‘, B’, C‘:
Since the computations are performed in a finite field, the properties of commutativity and associativity hold. The specific derivation process is as follows:
According to the verification equation, the computed result [A']_{1}[B']_{2} is consistent with the result of the original verification equation. Therefore, it can also pass the verification. This construction method is relatively simple, but note that x must be an element of the G1 field, and multiple proofs can be forged using this approach.
3.2 Additive Construction
Similarly, the following forged proof A‘, B’, C‘ can be constructed based on addition, where \eta is a random numner in the G_{1} field, and \delta is a trusted setup parameter that can be obtained from the verification_key. The method of obtaining the trusted setup parameters varies depending on the library used. Some libraries store them in a separate JSON file, while others store them in on-chain contracts. However, these parameters are publicly available and can be obtained.
The derivation process is as follows.
According to the verification equation, the computed result [A']_{1}[B']_{2} matches the right-hand side of the equation, thus passing the verification. This method can also construct multiple forged proofs.
3.3 Merged Construction
The above two ways of constructing a forgery proof can be combined into the following expression:
The corresponding implementation is available in the ark code base.
/// Given a Groth16 proof, returns a fresh proof of the same statement. For a proof π of a
/// statement S, the output of the non-deterministic procedure `rerandomize_proof(π)` is
/// statistically indistinguishable from a fresh honest proof of S. For more info, see theorem 3 of
/// [\[BKSV20\]](https://eprint.iacr.org/2020/811)
pub fn rerandomize_proof(
vk: &VerifyingKey<E>,
proof: &Proof<E>,
rng: &mut impl Rng,
) -> Proof<E> {
// These are our rerandomization factors. They must be nonzero and uniformly sampled.
let (mut r1, mut r2) = (E::ScalarField::zero(), E::ScalarField::zero());
while r1.is_zero() || r2.is_zero() {
r1 = E::ScalarField::rand(rng);
r2 = E::ScalarField::rand(rng);
}
// See figure 1 in the paper referenced above:
// A' = (1/r₁)A
// B' = r₁B + r₁r₂δ
// C' = C + r₂A
// We can unwrap() this because r₁ is guaranteed to be nonzero
let new_a = proof.a.mul(r1.inverse().unwrap());
let new_b = proof.b.mul(r1) + &vk.delta_g2.mul(r1 * &r2);
let new_c = proof.c + proof.a.mul(r2).into_affine();
Proof {
a: new_a.into_affine(),
b: new_b.into_affine(),
c: new_c.into_affine(),
}
}
4. Summary
This article primarily introduces the basic concepts, cryptographic foundations, and the main algorithm flow of the Groth16 algorithm. It also focuses on demonstrating the construction methods for three types of Groth16 transaction malleability attack. In the upcoming articles, we will further demonstrate verification attacks by attacking commonly used cryptographic libraries implementing the Groth16 algorithm.
References
https://medium.com/ppio/how-to-generate-a-groth16-proof-for-forgery-9f857b0dcafd
Contact Beosin