Co-authors banri, vita, and Hiro from Titania Research.
Thank you SoraSue and Masato for the discussion, and to Davide, Lin, donnoh, Vitalik and everyone who spoke with us at ZuBerlin.
TL;DR
This post explains the issues of predictability and manipulability in the traditional RANDAO used by the Ethereum Beacon Chain. It introduces a new approach called Unpredictable RANDAO, which reduces the number of possible future states an attacker can control from an exponential 2^k to a much smaller, linear k+1, even if they control k consecutive slots. Instead of relying on a single proposer to reveal a value, this method uses a committee-based Distributed Key Generation (DKG) and threshold signatures to produce the RANDAO reveal value. This makes it much harder to predict future randomness in advance and significantly weakens the economic incentives for attacks like Selfish Mixing or Forking.
1. Current RANDAO Mechanism
In Proof-of-Stake (PoS) consensus, having a fair source of randomness is critically important. On the Ethereum Beacon Chain, randomness is generated using RANDAO, and this randomness is used to select proposers two epochs ahead (i.e., for slots 33–64 into the future). (Randomness is also used for selecting attestation committees, but that is beyond the scope of this document.)
In the current RANDAO scheme, at each slot l, the selected proposer P_l generates a signature using their private key sk_l as follows:
Here, \mathrm{sign}_{\mathrm{BLS}} represents a BLS signature.
This signature \sigma_l is included in the block body directly as the RANDAO reveal value r_l:
Each attester verifies the validity of the signature using the proposer’s public key pk_l:
Here, \mathrm{verify}_{\mathrm{BLS}} is the BLS verification function.
Only if the verification is successful is r_l accepted, and the RANDAO mix value for slot l+1, denoted m_{l+1}, is updated using the following formula:
If the verification fails, the block is considered invalid, and the mix value remains unchanged.
At the final slot l of epoch e, the mix value is used to generate the seed S_{e+2} for proposer selection in epoch e+2:
Here, H denotes a hash function, and e+2 is converted to bytes before being concatenated.
2. Known Issues
If an attacker controls the last k slots of an epoch as the proposer, they can influence the proposer assignments in epoch n + 2 in their favor by choosing whether to propose or skip blocks in each slot—a binary decision per slot. This is possible because, under the current RANDAO mechanism, the proposer generates the reveal value for each slot. As a result, the attacker can simulate all 2^k combinations of propose/skip decisions in advance and predict how these affect future mix outputs.
Alpturer & Weinberg (2024)[1] formalized this manipulation of RANDAO—known as the Selfish Mixing attack—as a Markov Decision Process (MDP). Their study provides a theoretical framework analyzing how an attacker can strategically choose whether or not to propose blocks at the end of an epoch to bias the RANDAO output in the next epoch.
Specifically, they modeled the attack using the following state variables:
- the attacker’s stake ratio \alpha \in (0,1),
- the number of consecutive slots under the attacker’s control at the end of an epoch (the tail length) k,
- and the number of slots already controlled within the epoch (referred to as count).
Since the attacker can decide for each of the k slots whether to submit a block, the total number of possible strategies is 2^k. Based on this state space and action set, they numerically evaluated the attacker’s optimal strategy.
Their key findings are:
While the number of strategic options grows exponentially with the tail length k, the actual gain increases smoothly. This is due to the economic cost of skipping slots (which forfeits rewards) and the rapidly decreasing probability of obtaining a long tail, which is approximately \alpha^k.
They define the average proposer assignment ratio under attack as f_{\mathrm{attack}}(\alpha), and the honest baseline (equal to the stake ratio) as \alpha. The attacker’s excess gain is:
According to their analysis, \Delta(\alpha) reaches 1% only when the attacker controls around 25% of the stake (\alpha \approx 0.25). At \alpha = 0.20, the excess gain is only about 0.68%. In other words, an attacker with 20% stake executing the Selfish Mixing attack would achieve an average proposer assignment of 20.68%, just 0.68% above the honest baseline.
This implies that to obtain more than a 1% advantage using a tail of 2–3 slots, an attacker would need to control at least 25% of the stake.
The reason is that Selfish Mixing requires the attacker to intentionally skip block proposals in their assigned slots, which comes with an economic cost of forfeiting those rewards. Thus, for relatively small attackers (\alpha < 0.20), the strategy alone offers limited economic appeal.
In summary, while Selfish Mixing is a theoretically feasible attack, its profitability is suppressed for attackers with smaller stakes, whereas it becomes economically meaningful only when the attacker holds a substantial stake—roughly 25% or more.
However, a follow-up study by Nagy et al. (2025)[2] introduced a new attack vector—RANDAO Forking Attack—that demonstrated even more severe vulnerabilities in RANDAO.
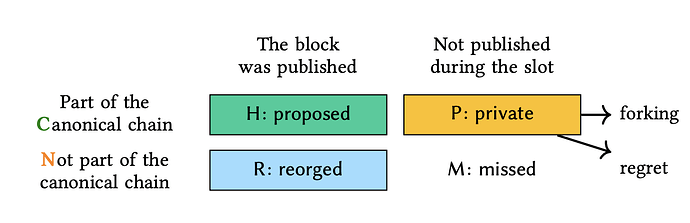
They showed that if an attacker controls slots near the epoch boundary, they can keep their own proposed blocks private and override (reorg) subsequent honest blocks, effectively removing them from the canonical chain.
This attack succeeds when the attacker’s stake \alpha and the proposer boost b satisfy the following inequality in the fork choice rule:
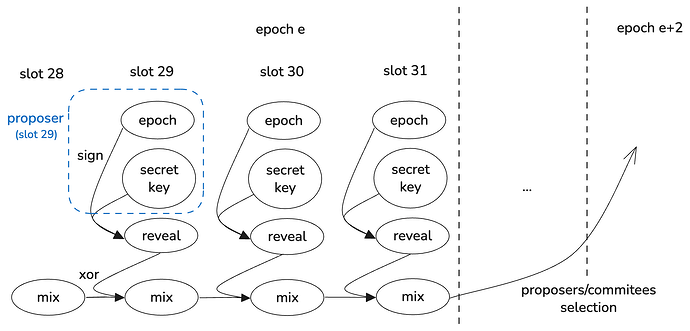
Nagy et al. (2025) illustrated this condition in the diagram below:
The diagram shows how an attacker, by controlling the last few slots of one epoch and the first few of the next, can hide their own proposed blocks, wait for honest proposers to publish theirs, and then reorganize the chain to exclude the honest blocks. This gives the attacker the ability to bias the mix value output in their favor.
This means that with just 20% of the stake (\alpha \ge 0.20), an attacker can trigger reorgs at specific slots to influence the RANDAO output.
Compared to Selfish Mixing, this Forking Attack has two major advantages:
-
No need for direct control over consecutive slots: Even if the attacker only controls slots 27, 28, 30, and 31 at the end of an epoch (and honest proposers control slots 29 and 32), they can reorg the honest blocks at 29 and 32 to simulate uninterrupted control and achieve similar predictability in the mix value.
-
No need to forfeit rewards: Unlike Selfish Mixing, this method doesn’t require attackers to skip or hide their own blocks. Instead, they only reorg the honest blocks, significantly reducing the cost of the attack.
Furthermore, Nagy et al. integrated both attacks into a unified MDP-based model and conducted numerical analyses to determine the optimal combined strategy. Their results showed that using Forking alongside Selfish Mixing allows even smaller attackers—those with around 8% stake—to gain extra rewards, which would not have been possible with Selfish Mixing alone.
Notably, they found that the stake ratio needed to dominate half the slots dropped from 46.24% (with only Selfish Mixing) to 41.95% when Forking was also employed.
They also quantified the impact on chain performance: with just 33% stake, throughput drops by around 3.9%, and with 30% stake, forks occur in approximately 18.9% of epochs. This demonstrates a significant degradation of user experience and trust in the Ethereum blockchain.
2.1 Clarifying the Problem
Based on the preceding discussion, the fundamental issues with Ethereum’s current RANDAO mechanism can be distilled into two key points:
- Predictability: If an attacker controls the last k slots (the “tail slots”), they can compute 2^k possible outcomes for the future randomness value.
- Manipulability: With this predictive power, an attacker can selectively choose not to propose a block or attempt a reorg of an honest block in order to maximize their own gain.
It’s important to note that predictability is the more critical issue compared to manipulability. No matter how much manipulability exists, if the attacker cannot predict the outcome of their actions, then from an incentive standpoint, the ability to manipulate is essentially meaningless.
The goal of this study is not to eliminate manipulability entirely, but rather to significantly reduce predictability. Specifically, by introducing a threshold signature scheme involving entities other than the block proposer, we aim to drastically limit an attacker’s ability to forecast the output of the randomness function, even if they control the final slots of an epoch.
This reduced predictability of the randomness value in turn lowers the economic incentives for withholding, discarding, or reorganizing blocks. The core thesis of this research is that by eliminating most of the predictability in the output of RANDAO, we can fundamentally weaken the economic motivation to manipulate it.
3. Our Proposal: Unpredictable RANDAO
In this proposal, we aim to address a fundamental flaw in the current RANDAO mechanism—namely, that the proposer can precompute the randomness. To resolve this, we eliminate the use of a single proposer to reveal randomness and instead introduce a committee of multiple validators. Using DKG and threshold signatures, this committee collaboratively generates the reveal value.
Specifically, the random reveal value for slot l+1, denoted as r_{l+1}, is generated as follows:
For slot l, we define a fixed committee size of n, and set the threshold number of signatures required for the threshold signature to be valid as t = \lfloor 2n/3 \rfloor + 1. In other words, more than two-thirds of the committee must sign for the threshold signature to be valid. This design ensures that no single validator can control the randomness; the value is finalized only when enough signatures are collected.
Each committee member A_{l,i} uses their individual share s_{l,i} to produce a signature share \sigma_{l,i} based on the current slot l:
Here, \mathrm{sign}_{\mathrm{share}} represents the function for generating a signature share within the threshold signature scheme.
Once at least t signature shares are collected, they can be combined into a unique aggregated signature \Sigma_l using the threshold signature scheme:
T_l denotes the set of indices for validators who submitted signature shares, and \mathrm{combine} is the aggregation function used in BLS threshold signatures.
The resulting aggregated signature \Sigma_l is then included in the block for slot l+1 as the reveal value:
The proposer for slot l+1 must include this aggregated signature \Sigma_l (i.e., the reveal value) in the block they propose. This aggregated signature must satisfy the following verification condition:
Here, \mathrm{PK}_l is the aggregate public key of the committee for slot l, and \mathrm{verify}_{\mathrm{th.sig}} is the verification function for the threshold signature.
Attesters must ensure that the following two conditions are met when validating a block:
- The proposed block contains the aggregated signature \Sigma_l (as the reveal value).
- The included reveal value is a valid aggregated signature that passes the above verification.
If either of these conditions is not met, attesters must reject the block (i.e., vote 0), and the block will not be included in the canonical chain.
This approach ensures that even if an attacker controls multiple consecutive tail slots, they cannot unilaterally manipulate the reveal values. As a result, their ability to predict future mix values is significantly weakened.
A key technical point here is the uniqueness of the threshold signature. As long as t out of n committee members provide valid signature shares, the resulting aggregated signature is deterministically unique and does not depend on which t members signed. Moreover, unless an attacker controls a majority and knows their private keys, the final value remains unpredictable.
In other words, threshold signatures enable the generation of values that are unpredictable in advance and immune to manipulation by the proposer—aside from the inherent unpredictability of whether a proposer will propose a block at all. Even if some malicious actors are present in the committee, their decision to sign or not does not impact the final result.
This inherent property of threshold signatures is what makes it possible for our proposal to make RANDAO truly unpredictable.
Finally, note that our proposal only changes the source of the reveal value; the way mix values and seed values are computed remains unchanged.
3.1. Design
3.1.1. IL Committee
While one option would be to establish a new, dedicated committee specifically for RANDAO, we have chosen instead to expand the responsibilities of the existing IL Committee[3]. Adding too many members can make DKG difficult from a performance standpoint, but th IL Committee, which consists of 16 members, is a suitable size in this regard. Additionally, assigning more responsibilities to an existing committee helps keep the protocol design simpler than introducing a new one.
The IL Committee originally proposed in FOCIL had no economic incentives. However, in this mechanism, the absence of such incentives would cause the system to fail. Therefore, when introducing this Unpredictable RANDAO, we believe it is necessary to add an attestation reward for members who submit signature shares. In practice, a more detailed reward structure should be designed when integrating this into the protocol.
3.1.2. Fast Batched Asynchronous DKG
For secret sharing, we have chosen Fast Batched Asynchronous DKG[4]. Classical schemes like Pedersen DKG are not suitable for our purposes due to performance constraints. Fast Batched Asynchronous DKG operates in a fully asynchronous model and maintains Byzantine fault tolerance for up to t < n/3, while ensuring that each node’s communication overhead is largely independent of committee size. According to the evaluation in the original paper, the scheme can generate 50,000 pre-signatures per second even with n=49 and t=16, making it well-suited for use with a 16-member IL Committee. Additionally, because Fast Batched Asynchronous DKG eliminates polynomial commitments entirely and significantly reduces both the O(n^2) communication cost and high round complexity of Pedersen-based DKGs, it is easier to meet practical bandwidth and latency constraints.
3.1.3. BLS Threshold Signature
For the threshold signature scheme, we selected the BLS Threshold Signature[5], which can be naturally extended from the current BLS signature specification. It can be implemented with minimal changes while continuing to use the same elliptic curve (BLS12-381) and pairing functions. In the context of the Beam Chain[6] architecture, it may be worth exploring other threshold signature schemes that are better suited to algorithms like FALCON[7].
3.2. Overall Process
This section outlines the overall process in which committee members perform DKG to share a secret and generate a threshold signature. The proposer then includes the resulting reveal value in the beacon block body.
Note that the following is a simplified, abstracted overview. The actual details may vary depending on how the committee is formed, which DKG method is used, and the chosen threshold signature scheme.
For example, in the Fast Batched Asynchronous DKG used in our proposal, the concept of a “commitment” (C_i) doesn’t exist. However, the essential steps can still be represented by the following flow.
3.2.1. Notation
-
n: Number of committee members
-
t = \lfloor 2n/3 \rfloor + 1: Threshold
-
l: Slot number
-
i: Index of a committee member
-
P_l: Proposer for slot l
-
A_{l,i}: The i-th committee member for slot l
-
f_{l,i}: Polynomial generated by committee member A_{l,i}
-
a_{l,i,j}: The j-th coefficient of f_{l,i} (0 \le j \le t-1)
-
C_{l,i,j}: Commitment to coefficient a_{l,i,j}
-
H: Hash function (mapping to group G_1)
-
s_{l,i \rightarrow j} = f_{l,i}(j): Share sent from A_{l,i} to A_{l,j}
-
s_{l,i} = \sum_j s_{j \rightarrow i}: Combined share for A_{l,i} used in threshold signature
-
pk_{l,i}: Public key share of A_{l,i} for slot l
-
PK_l: Aggregated public key of the committee for slot l
-
\mathrm{verify}_{\mathrm{DKG}}(C_{l,i,j}, s_{l,j \rightarrow i}): Function to verify DKG share
-
\mathrm{verify}_{\mathrm{th.share.sig}}(pk_{l,i}, l, \sigma_l): Verifies individual threshold signature share \sigma_{l,i}
-
{\mathrm{verify}_{\mathrm{th.sig}}}(PK_l, l, \Sigma_l): Verifies the aggregated signature \Sigma_l
-
\mathrm{sign}_{\mathrm{th.share.sig}}(s_i, l): Signs slot l using share s_i
-
\sigma_{l,i}: Signature share from A_{l,i}
-
T_l: Set of committee member indices who signed in slot l, with |T_l| \ge t
-
\mathrm{combine}(\{\sigma_{l,i}\}_{i \in T_l}): Combines individual signature shares
-
\Sigma_l: Aggregated signature for slot l
-
r_l = \Sigma_{l-1}: Reveal value for slot l
-
m_l = \mathrm{xor}(m_{l-1}, r_l): Mix value for slot l
3.2.2. Overall Process
1. Share Generation Phase (at the first slot l' of epoch e-1)
-
Election Check (committee member, slot l'): Each participant checks if they are selected as a committee member.
-
Polynomial Generation (committee member, slot l'): Each member generates their own polynomial f_{l',i} with coefficients a_{l',i,0}, a_{l',i,1}, ..., a_{l',i,t-1}.
-
Commitment Broadcasting (committee member, slot l'): Each member calculates and broadcasts their commitment C_{l',i,j}.
-
Share Distribution (committee member, slot l'): Each member calculates s_{l,i \rightarrow j} and sends it to the appropriate member.
-
Share Verification (committee member, slot l'): Each member verifies the shares they received using \mathrm{verify}_{\mathrm{DKG}}.
-
Share Calculation (committee member, slot l'): Each member calculates their own share s_{l',i}.
-
Key Storage: Each member computes their public key share pk_{l',i} and the overall committee public key PK_{l'}, storing them in the chain state.
2. Threshold Signing Phase (for each slot l in epoch e)
-
Signature Share Generation (committee member, slot l): Each member computes their signature share \sigma_{l,i}.
-
Signature Share Broadcasting (committee member, slot l): Each member broadcasts their \sigma_{l,i}.
-
Signature Share Verification (proposer, slot l+1): The proposer verifies each received \sigma_{l,i} using \mathrm{verify}_{\mathrm{th.share.sig}}.
-
Aggregated Signature Generation (proposer, slot l+1): The proposer combines enough signature shares to compute the aggregated signature \Sigma_l.
-
Aggregated Signature Verification (proposer, slot l+1): The proposer verifies \Sigma_l using \mathrm{verify}_{\mathrm{th.sig}}.
-
Mix Value Calculation (proposer, slot l+1): The proposer computes the next mix value m_{l+1} using m_l and r_{l+1} = \Sigma_l.
-
Block Proposal (proposer, slot l+1): The proposer constructs and broadcasts a beacon block including r_{l+1} in the block body.
-
Block Verification and Voting (attester, slot l+1): Attesters verify the validity of r_{l+1} using PK_l and \mathrm{verify}_{\mathrm{th.sig}}.
A key point to emphasize is that if the proposer is malicious, they cannot predict their expected reward from block proposal until after step 4 above is completed. In contrast, under the current RANDAO scheme, this can be predicted more than an epoch in advance. With this new method, a proposer only learns the mixed value–derived from \Sigma_l –after they are selected and perform some computation, making manipulation harder.
3.3. Specification
This section defines the specification. Since many details are still undecided, we will focus here solely on the core concept: the proposed change to how randao_reveal is handled.
In the current specification, the value assigned to randao_reveal in the BeaconBlockBody is the epoch_signature:
block.body.randao_reveal = epoch_signature
This epoch_signature is obtained from the following function:
def get_epoch_signature(state: BeaconState, block: BeaconBlock, privkey: int) -> BLSSignature:
domain = get_domain(state, DOMAIN_RANDAO, compute_epoch_at_slot(block.slot))
signing_root = compute_signing_root(compute_epoch_at_slot(block.slot), domain)
return bls.Sign(privkey, signing_root)
Our proposal is to replace this with:
block.body.randao_reveal = threshold_signature
The threshold_signature is obtained from the following function:
def get_threshold_signature(
state: BeaconState,
block: BeaconBlock,
inclusionLists: List[InclusionList, IL_COMMITTEE_SIZE],
) -> BLSThresholdSignature:
domain = get_domain(state, DOMAIN_RANDAO, compute_epoch_at_slot(block.slot))
signature_shares = []
for il in inclusionLists:
signature_share = il.randao_signature_share
signing_root = compute_signing_root(block.slot, domain)
pubkey_share = compute_pubkey_share(state, il)
assert thBls.Verify(pubkey_share, signing_root, signature_share)
signature_shares.append(signature_share.signature)
pubkey_shares.append(pubkey_share)
combined_signature = thBls.Combine(signature_shares)
combined_pubkey = thBls.CombinePKs(signature_shares)
combined_signing_root = compute_signing_root(block.slot, domain)
assert thBls.CombinedVerify(combined_pubkey, combined_signing_root, combined_signature)
return combined_signature
Here, signature_share is taken from each InclusionList. In other words, we extend the InclusionList structure proposed in FOCIL by adding a new field, redefining it as follows:
class InclusionList(Container):
slot: Slot
validator_index: ValidatorIndex
inclusion_list_committee_root: Root
transactions: List[Transaction, MAX_TRANSACTIONS_PER_INCLUSION_LIST]
# newly added field
randao_signature_share: BLSSignatureShare
3.4. Consideration
In the traditional RANDAO approach, if an attacker controls several consecutive slots at the end of an epoch, they can choose, for each slot, whether to include or omit a signature using their own private key. This creates a binary decision per slot, leading to an exponential number of possible strategy patterns—specifically, 2^k for k slots. As a result, the attacker can compute all 2^k possibilities and select the outcome most favorable to them.
In contrast, under our proposed method, randomness for each slot l is not generated by a single proposer. Instead, it is determined through threshold signatures by a committee. This means the attacker can no longer compute the reveal value in advance on their own. Unless they control more than two-thirds of the committee, they cannot predict future reveal values.
When this setup is modeled, the reveal value for each slot behaves like a source of randomness that the attacker cannot control. The number of possible reveal values for any slot is fixed independently of the attacker’s intent. Even if an attacker controls consecutive slots, the unpredictability of the reveal values for each slot limits their ability to plan future actions. Therefore, once a reveal value is finalized for one slot, the attacker’s strategic options for the following slot become constrained based on that value. As a result, the number of possible states the attacker can compute drops from 2^k to just k + 1.
To be more specific, consider a scenario where the attacker controls k consecutive slots. In the traditional setup, the attacker can compute 2^k possible outcomes. However, in our proposal, each slot’s reveal value is sequentially finalized via committee-based threshold signatures. This prevents the attacker from knowing future reveal values in advance. Once the reveal value for the first slot is determined, the attacker must base their next move on that value—while the reveal values for subsequent slots remain undecided and unpredictable.
This process is repeated for each slot, meaning the attacker cannot precompute a complete strategy. Instead, they must re-evaluate their actions at every slot as new reveal values are determined. Therefore, even if the attacker controls k consecutive slots, the number of possible reveal value scenarios grows only linearly with k, not exponentially. Specifically, starting from the first reveal value—which is out of the attacker’s control—subsequent values are determined one by one, adding just one possible strategic choice at each step. Consequently, the number of prediction scenarios the attacker must consider is limited to a maximum of k + 1, rather than 2^k.
For these reasons, our proposed reveal value generation mechanism fundamentally blocks attackers from precomputing future reveal values. The economically rational choice for an attacker, then, becomes to behave honestly—proposing blocks without engaging in intentional reorganizations or block withholding.
4. Design Space for Unpredictable RANDAO
In our proposed approach above, we adopt the IL committee from the FOCIL[3:1] specification, use Fast Batched Asynchronous DKG[4:1] for the secret sharing scheme, and employ BLS threshold signatures[5:1] for the signing mechanism. However, there remains room for design choices in each of these areas.
-
Committee
- What should the committee size be?
- How frequently should the committee be updated?
- Should we create a new RANDAO committee, or select from existing committees?
- How should incentives be designed?
-
DKG
- Which DKG protocol should be used?
- (Is it acceptable to depend on specialized hardware?)
-
Threshold Signatures
- Which threshold signature scheme should be used?
- What should the signature threshold be?
- Who is responsible for aggregating the signature shares and public keys?
-
RANDAO
- Should the update frequency be based on epochs or slots?
- Should a block that fails to include a reveal value be treated as a missed slot?
5. Discussion
5.1. Reduction of the Attacker’s State Space and Its Impact on Economic Incentives
This proposal aims to reduce the incentive for attackers to manipulate RANDAO by shrinking the attacker’s predictable state space from an exponential size of 2^k to a linear size of k+1 when they control consecutive slots. However, while this reduction in the theoretical state space is promising, this paper does not yet offer a quantitative analysis of how much it actually reduces an attacker’s economic incentive.
For real-world attackers, the size of the state space is less important than the expected payoff from an attack. The attacker’s goal is to increase their probability of being selected as a proposer in the next epoch, thereby gaining additional rewards. If the benefit does not outweigh the cost of the attack, then there is no incentive to proceed. Therefore, to truly evaluate the effectiveness of this proposal, it is essential to quantitatively assess how the reduction in state space impacts concrete economic incentives.
In particular, approaches like those used by Alpturer & Weinberg (2024) or Nagy et al. (2025)—such as MDPs or agent-based simulations—should be employed to evaluate:
- How the reduced state space affects the attacker’s optimal behavior policy
- The attack’s return on investment under various configurations of stake ratios, committee sizes, and threshold settings
Only through such analysis can we demonstrate that this proposal meaningfully reduces real-world economic incentives to attack, thereby substantiating its practical effectiveness.
5.2. Liveness Challenges from Introducing DKG and Threshold Signatures
This proposal introduces powerful mechanisms—DKG and threshold signatures by committees—to significantly reduce predictability. However, this increased robustness also introduces new challenges, particularly with regard to blockchain liveness.
To enable threshold signatures, a sufficient portion of the committee must provide their signature shares within a short time frame. This requirement introduces the following risks:
-
Network Delay and Fault Tolerance:
In real-world internet environments, communication delays and failures between nodes are common. If a sufficient number of committee members cannot submit their signatures in time, block proposals may halt, compromising chain availability.
One possible countermeasure is to allow block proposals even without an updated reveal value. In this case, blocks without a reveal value could continue to be produced even if less than two-thirds of signatures are collected, and transactions would still be included. If the reveal value is not updated for over one epoch, the protocol could revert to the original RANDAO mechanism—similar to an inactivity leak strategy. -
Potential for Share Withholding Attacks:
If an attacker controls part of the committee, they could intentionally withhold their signature shares, causing a temporary halt in the chain. Just as economic disincentives can suppress manipulation, this scenario illustrates that attackers may gain new opportunities for DoS attacks.
Given these points, future research must quantitatively evaluate both the economic deterrence this proposal provides and the impact of DKG and threshold signatures on liveness in real-world network conditions. Based on those findings, it will be crucial to develop appropriate parameter settings and design supplementary fail-safes to maintain system robustness.
6. Conclusion
This post approached the problem of attack incentives in RANDAO by focusing on the predictability of its randomness generation process. From this perspective, we proposed an Unpredictable RANDAO that (i) reduces the attacker’s state space from exponential to linear, and (ii) makes the cost of attack less favorable than honest participation. By incorporating a committee-based DKG and threshold signatures, even if an attacker controls multiple consecutive slots at the end of an epoch, they are unable to precompute future reveal values. As a result, the expected profit from block rejections or reorgs rapidly diminishes.
Our mathematical model shows that the number of computable scenarios when controlling k consecutive slots is reduced from 2^k to k+1. This suggests that the surplus profit thresholds previously required for attacks—over 25% for selfish mixing alone and over 8% when combined with forking—effectively vanish. The actual degree of reduction is left as a topic for future work.
In terms of design space, several parameters remain to be explored, including committee size and update frequency, the choice of DKG protocol, and the threshold settings. Future challenges include analyzing trade-offs with application latency requirements and network synchronization characteristics. Nonetheless, this proposal demonstrates that eliminating predictability itself can institutionally undermine attack incentives and fundamentally strengthen the randomness foundation of Proof-of-Stake chains. This marks a significant step forward in the pursuit of a simpler yet more secure Beacon Chain design.
Forking the RANDAO: Manipulating Ethereum’s Distributed Randomness Beacon ↩︎
EIP-7805: Fork-choice enforced Inclusion Lists (FOCIL) ↩︎ ↩︎
Threshold Signatures, Multisignatures and Blind Signatures Based on the Gap-Diffie-Hellman-Group Signature Scheme ↩︎ ↩︎
Falcon: Fast-Fourier Lattice-based Compact Signatures over NTRU ↩︎