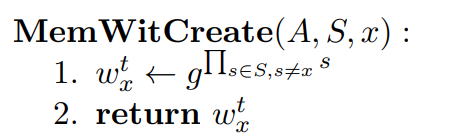I find the RSA accumulator interesting and want to explore some ideas about privacy with it. However, I am afraid I missed something since I’m not really good at cryptography. So I want to put forward a brief summary of my thoughts and ask some (maybe stupid) questions. Thanks for reviewing and answering🙏
I want to use an RSA accumulator to represent a set S, without disclosing members of S. The accumulator value, A, is stored in a smart contract. The product p of all elements which are already added is also stored in the smart contract. Anyone could add elements to S (and update A, p accordingly). Anyone could generate membership proof and non-membership proof on A and the smart contract could verify. What I want to achieve is that nobody (neither users nor smart contract) knows the set members. Following are statements I’m not sure about:
Can we update
Awithout disclosing the newly added elements?
I think we can, if we restrict that we have to aggregate at least 2 elements and add them to A at once. Elements of the RSA accumulator should be primes. To aggregate two primes a1 and a2, the user computes the product a = a1 * a2 mod N and submits a, then the smart contract computes the new accumulator value A' = A^a mod N. Nobody can find out a1 and a2 from a since big integer factorization is hard.
This solution may cause inconvenience in application since sometimes we just want to add one element. Are there some better ways?
Can we generate membership proof without disclosing the members of S?
I think we can. To generate membership proof w for element x, the user computes w = A ^ (x^-1) mod N.
In Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains, a simpler method is used: re-compute the accumulator from the base accumulator value g using all set members except x.
This requires making public
S members, which I think could be avoided.
Can we generate non-membership proof without disclosing the members of S?
I think we can, if we disclose the product p of all elements which are already added. p is stored in the smart contract along with A. To update, the smart contract computes p' = p * a mod N (should it mod N?). To generate non-membership proof (u, v) for x, the user finds out a pair (u, v) which makes u * x + v * p = 1. I think making public p doesn’t leak information about the set members. But is it practical to store and update p?
Besides, I also found the paper Vulnerability of a non-membership proof scheme which seems to propose 4 attacks targeting RSA accumulator. I have to say it’s too difficult for me to comprehend this paper. I just want to know is it still safe to use RSA accumulator?
Looking forward to comments, thanks a lot!