At Vocdoni, we’ve spent the last six years advancing decentralized voting solutions, focusing on bridging web2 applications with web3 technologies. We’ve successfully executed high-stakes voting for organizations such as football clubs, city councils, associations, political parties, professional bodies, movements under prosecution and more.
Until today, we have been relying on a customized proof-of-authority Layer 1 network.
But we believe it’s now time to transition to a zero-knowledge (zk) based infrastructure to achieve full decentralization and address the main challenges of digital voting systems
On the road to this new protocol implementation, we would like to receive feedback from the Ethereum community ![]() .
.
By taking ideas from our expertise, MACI, and others. We introduce a new universal voting protocol that tackles critical issues like receipt-freeness, voter privacy, scrutiny transparency, universal auditing, and eliminating the need for a trusted coordinator.
Designed for scalability and accessibility, the system enables high-frequency, low-cost voting suitable for mass adoption. We laverage on zkSNARKs and threshold homomorphic encryption (ElGamal), to ensure end-to-end verifiability and anonymity for the end user.
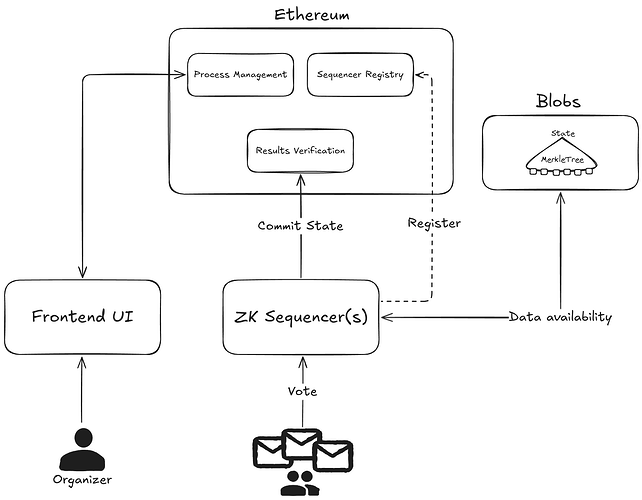
A decentralized zkSNARK-based state machine, operating as specialized layer 2 on the Ethereum blockchain, provides censorship-resistance, integrity, trutless operation and a transparent scrutiny of results. A distributed key generation (DKG) among sequencers, coordinated via smart contracts, allows for secure and decentralized encryption key creation without reliance on a central authority.
Most components have been implemented using accessible technologies and have undergone proof-of-concept testing, confirming that the protocol is practical and ready for immediate deployment. We plan to launch the testnet in Q1–Q2 2025.
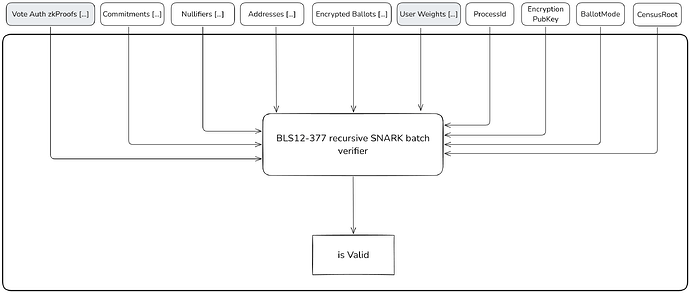
Our implementation uses Circom and SnarkJS on the voter side, enabling voting from any device, including smartphones and web browsers. For the sequencers, we use Gnark with curves BLS12-377 and BW6-761 for native recursion in vote aggregation. This setup produces a final BN254 proof that can be verified on Ethereum.
Focusing on decentralization, we designed the sequencer to operate on accessible machines—CPU-based systems with 64 GiB of memory—so that participation doesn’t require specialized hardware.
Actors
Organizers set up and manage voting processes, defining parameters such as voting options, duration, and voter registries (census).
Voters interact with the system through user-friendly interfaces, enabling them to cast their votes securely and privately. Voters generate zkSNARKs to prove that their encrypted votes comply with voting rules without revealing their choices.
Sequencers are specialized nodes responsible for collecting votes, verifying their validity, and updating the shared state. They participate in the Distributed Key Generation (DKG) protocol to collaboratively generate encryption keys without any single party controlling the private key.
Properties
Privacy is maintained using homomorphic encryption. Votes are encrypted with the ElGamal cryptosystem over elliptic curves, allowing the aggregation of encrypted votes without decrypting individual ballots, thus keeping voter choices confidential.
Integrity is ensured through the collaborative efforts of a decentralized network of sequencers, who maintain a shared state represented by a Merkle tree that summarizes the current status of the voting process, including accumulated votes and nullifiers to prevent double voting. Each time the state is updated with new votes, a sequencer generates a zkSNARK proof attesting to the validity of the state transition.
Receipt-freeness is achieved by preventing voters from being able to prove to third parties how they voted, mitigating risks of coercion and vote-buying. This is accomplished through ballot re-encryption and vote overwriting mechanisms. When a voter submits an encrypted ballot, sequencers re-encrypt it before storing it in the state, making it computationally infeasible to link the original and re-encrypted ciphertexts. Voters are also allowed to overwrite their votes; if a voter casts a new vote, the sequencer subtracts the previous encrypted vote from the tally and adds the new one. Regular re-encryption of random ballots by sequencers conceals when overwrites occur, enhancing receipt-freeness by making it indistinguishable whether a ballot was overwritten or simply re-randomized.
End-to-End Workflow
- Process Initialization: The organizer defines the voting parameters—including options, duration, and census—and registers the new process on the Ethereum blockchain via smart contracts.
- Distributed Key Generation (DKG): Sequencers collaboratively execute the DKG protocol to generate the collective public encryption key without any single party knowing the private key. The generated public key is published on-chain for voters to use when encrypting their ballots.
- Voter Preparation: Voters retrieve the public encryption key and their inclusion proof (Merkle proof) from the census registry.
- Vote Casting: Voters select their choices and encrypt their ballots using the public key. Generate zkSNARK proofs to prove the validity of their encrypted votes without revealing their selections. Encrypted ballots and proofs are submitted to a sequencer for processing.
- Vote Collection and Verification: Sequencers verify the zkSNARK proofs to ensure each vote complies with the protocol rules. Confirm that the voter is eligible and has not already voted, or handle vote overwrites appropriately. Valid encrypted votes are aggregated homomorphically, allowing for tallying without decryption. The sequencer updates the State Merkle Tree to reflect new votes and nullifiers.
- State Transition and Proof Submission: Sequencers create zkProofs attesting to the validity of the state transition from the previous state to the new one. The new root and corresponding proof are submitted to the Ethereum smart contract. The contract verifies the data and updates the stored state root.
- Data Availability: Necessary data to reconstruct the state is published to the data availability layer (Ethereum data blobs), ensuring accessibility for verification and reconstruction of the new state.
- Process Finalization: At the end of the voting period, the process is finalized on-chain, and no further votes are accepted.
- Result Decryption: Sequencers collaborate to decrypt the aggregated vote totals using the threshold decryption protocol. Decrypted results are published on-chain, providing an immutable and transparent outcome.
Threshold Homomorphic Encryption
The system utilizes the ElGamal threshold encryption scheme over the elliptic curve bn254, which provides additive homomorphic properties essential for securely aggregating votes.
Encryption
A voter’s choice is represented as a message m \in \mathbb{Z}_q. To encrypt the vote:
- The voter encodes the message as a point on the elliptic curve: M = m G.
- The voter selects a random scalar k \in \mathbb{Z}_q^*.
- The ciphertext is computed as: C = (C_1, C_2) = (k G, M + k H).
Homomorphic Addition
The ElGamal cryptosystem over elliptic curves supports additive homomorphism for messages represented as points. Given two ciphertexts (C_1^{(1)}, C_2^{(1)}) and (C_1^{(2)}, C_2^{(2)}), their component-wise addition yields:
- C_1^{(\text{sum})} = C_1^{(1)} + C_1^{(2)}
- C_2^{(\text{sum})} = C_2^{(1)} + C_2^{(2)}
The aggregated ciphertext decrypts to the sum of the messages: M^{(\text{sum})} = M_1 + M_2
Threshold Decryption
After the voting period ends, the sequencers collaboratively decrypt the aggregated ciphertext. Each sequencer P_j computes a partial decryption share:
- Compute: D_j = s_j C_1.
- The partial decryptions are combined using Lagrange interpolation coefficients \lambda_j:
D = \sum_{j \in T} \lambda_j D_j = s C_1
where T is a set of at least t sequencers. - The plaintext message is recovered by computing:
M = C_2 - D = M + k H - s k G = M - The final result m is obtained by solving M = m G, which yields m.
Distributed Key Generation (DKG)
To eliminate the need for a trusted authority, the encryption key used for ballot encryption is generated collaboratively by the sequencers through a Distributed Key Generation protocol, which proceeds as follows:
- Initialization: Let G be the generator of an elliptic curve group of prime order q. The threshold t and the number of sequencers n are predefined, with t \leq n.
- Secret Sharing: Each sequencer P_i randomly selects a secret polynomial f_i(x) of degree t - 1, where f_i(0) = a_{i,0}, and the coefficients a_{i,j} are chosen uniformly at random from \mathbb{Z}_q.
- Commitments: Each sequencer publishes commitments to their polynomial coefficients: C_{i,j} = a_{i,j} G \quad \text{for} \quad j = 0, \ldots, t - 1.
- Share Distribution: Sequencer P_i computes shares for every other sequencer P_j: s_{i,j} = f_i(j), \quad \text{for} \quad j = 1, \ldots, n
These shares are securely transmitted to the respective sequencers using a simplified version of ECIES. - Verification: Each sequencer P_j verifies the received shares s_{i,j} by checking: s_{i,j} G \stackrel{?}{=} \sum_{k=0}^{t - 1} C_{i,k} \cdot j^k
- Private Key Share Computation: Each sequencer computes their private key share: s_j = \sum_{i=1}^n s_{i,j} \mod q
- Public Key Computation: The collective public key is computed as: H = \sum_{i=1}^n C_{i,0} = s G, where s = \sum_{i=1}^n a_{i,0} \mod q is the aggregate private key known only in a distributed form among the sequencers.
The Vote
The vote consists of several components and mechanisms listed below.
Process Identifier: A unique identifier \text{ProcessId} for the voting process. This ensures that votes are correctly associated with the specific voting event and prevents cross-process interference.
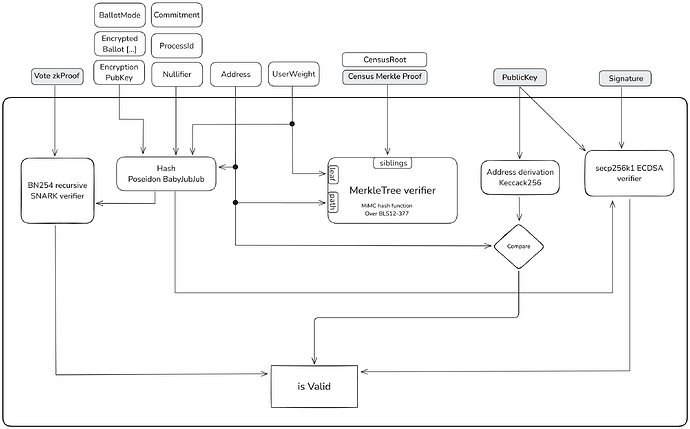
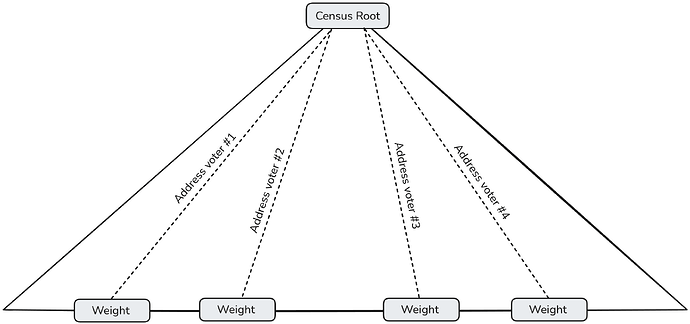
Census Proof: A Merkle proof demonstrating the voter’s inclusion in the authorized voter registry (census). This proof allows the sequencers to verify the voter’s eligibility without revealing the entire voter list, preserving privacy and efficiency.
Identity Commitment: The voter computes a commitment using a cryptographic hash function: C = Hash(\text{Address} \parallel \text{ProcessId} \parallel s), where H is a cryptographic hash function, \text{Address} is the voter’s unique identifier (such as a public key or an address), and s is a secret known only to the voter.
By incorporating the secret s into the commitment C, we effectively detach the nullifier from any direct association with the voter’s identity in the publicly accessible data. This means that even if future quantum computing advancements were to compromise the ElGamal encryption and reveal the contents of encrypted ballots, there would be no practical method to link a decrypted ballot back to a specific voter’s address using the nullifier.
Nullifier: To prevent double voting and handle vote overwriting, the voter computes a nullifier: N = Hash(C \parallel s). The nullifier acts as a one-time token that uniquely represents the voter’s participation without revealing their identity.
By avoiding the use of the private key or deterministic signatures when computing the nullifier, we ensure compatibility with hardware wallets and non-deterministic signature schemes.
Ballot: The ballot represents the voter’s choices as an array of individual selections that must adhere to the ballot protocol rules defined by the organizer. This flexible approach allows the protocol to support various voting configurations, including range voting, ranking, quadratic voting and more.
Suppose an organizer wants to implement a quadratic voting system with the following parameters:
- Maximum Selections: Up to 5 options can be selected.
- Value Range: Each selection must be a non-negative integer.
- Total Cost Constraint: The sum of the squares of the selections must not exceed a budget of 100 credits.
- Unique Values Constraint: Duplicate values are allowed.
The protocol would enforce that for a ballot \mathbf{m} = (m_1, m_2, \ldots, m_5):
- Each m_i \geq 0.
- \sum_{i=1}^5 m_i^2 \leq 100.
Encryped Ballot: The voter encrypts their ballot using the homomorphic ElGamal encryption scheme, proceeding as follows:
- The voter’s choices are encoded into a message vector \mathbf{m} = (m_1, m_2, \ldots, m_n), where each m_i corresponds to a selection in the ballot array.
- Each element m_i is encoded as a point on the elliptic curve: M_i = m_i G, where G is the generator of the curve.
- The voter selects a random scalar k \in \mathbb{Z}_q^*, where q is the order of the curve.
- The ciphertext is computed as: C = (C_1, C_2) = \left( k G,\; \sum_{i=1}^n M_i + k H \right)
where H is the public key obtained from the Distributed Key Generation protocol.
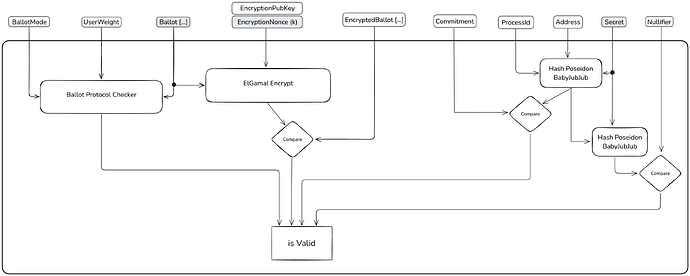
Zero-Knowledge Proof (zkSNARK): The voter generates a zkSNARK that proves, without revealing the ballot content, that:
- Correct Encryption: The encrypted ballot is correctly formed according to the encryption scheme.
- Protocol Compliance: The voter’s selections adhere to the ballot protocol rules defined by the organizer.
- Correct Nullifier and Commitment: The nullifier and commitment are correctly computed using the voter’s secret s and address.
- Knowledge of Secrets: The voter knows the secret s and the random scalar k used in encryption.
Signature: The voter signs necessary components of the vote using their private key associated with their address. This authenticates the vote and binds it to the voter’s identity in a verifiable manner. Many signature schemes may be supported (ECDSA, EdDSA, RSA, etc.).
State Transitions
The State Merkle Tree is a cryptographic data structure that allows efficient and secure verification of the data it contains. The tree is structured to store various types of information at predefined indices or addresses:
- Process Parameters: Stored at static indices, containing essential information such as the \text{ProcessId}, the root of the census Merkle tree (\text{censusRoot}), ballot protocol configurations, and the public encryption key H generated through the DKG protocol.
- Results Accumulators: Two accumulators are maintained to handle vote additions and subtractions:
- Addition Accumulator (C_{\text{add}}): Stores the homomorphically aggregated encrypted votes that have been added to the tally.
- Subtraction Accumulator (C_{\text{sub}}): Stores the homomorphically aggregated encrypted votes that have been subtracted due to vote overwrites.
- Nullifiers: Stored to prevent double voting. Each nullifier N is associated with a voter’s commitment and is unique to that voter for the specific voting process.
- Commitments: Stored to keep track of voter participation and to facilitate vote overwriting.
Sequencers are responsible for processing new votes and updating the shared state. Each state transition involves the following steps:
-
Batch Collection of Votes: The sequencer collects a batch of up to N new votes from voters. Batching votes enhances efficiency and scalability, allowing the sequencer to process multiple votes simultaneously. The value of N is determined by system parameters that balance computational constraints and network throughput.
-
Verification of Votes: For each vote in the batch, the sequencer performs:
- zkSNARK Proof Verification: Ensures that the zero-knowledge proof submitted with each vote is valid and that the vote complies with the protocol rules, including correct encryption, adherence to ballot protocol constraints, and proper computation of the nullifier and commitment.
- Eligibility Check: Verifies the voter’s eligibility by checking the provided census Merkle proof against the stored \text{censusRoot} in the state.
- Double Voting Prevention: Checks whether the nullifier N already exists in the state. If it does not, the vote is processed as a new vote. If it does, the vote is considered a vote overwrite.
-
Handling Vote Overwrites: If a voter submits a new vote with the same nullifier N, the sequencer:
- Subtracts the previous encrypted vote from the subtraction accumulator C_{\text{sub}}.
- Adds the new encrypted vote to the addition accumulator C_{\text{add}}.
- Replaces the new encrypted ballot within the State.
-
Random Re-encryptions: To enhance receipt-freeness and prevent linkage between votes and voters, the sequencer performs random re-encryptions of existing encrypted ballots:
- Selects a random subset of encrypted ballots in the state.
- Re-encrypts each selected ballot by adding an encryption of zero, using a new random scalar.
- Updates the encrypted ballots in the state with the re-encrypted versions.
-
Homomorphic Aggregation of Votes: The sequencer updates the accumulators using the homomorphic properties of the ElGamal encryption:
-
Generation of State Transition zkSNARK: The sequencer generates a zkSNARK proof that attests to the validity of the state transition from the previous root \text{Root1} to the new root \text{Root2}. The zkSNARK proof verifies all previous constraints and operations.
-
On-Chain Submission: The sequencer submits:, the updated state root \text{Root2}. The proof attesting to the validity of the state transition. A hash commitment to the data blob containing the votes and state updates, ensuring data availability.
The Vocdoni Token (VOC)
Vocdoni introduces a new token (VOC) to align incentives among participants and ensure the sustainability of the decentralized voting ecosystem. The token serves multiple essential functions: it incentivizes sequencers, facilitates payments for voting processes, and enables decentralized governance.
Sequencers must stake tokens as collateral to participate in the network, promoting honest behavior and network security. They earn rewards in VOC tokens based on their contributions to processing valid votes and maintaining the network’s integrity.
Organizers use tokens to pay for creating and managing voting processes. The costs depend on factors such as the maximum number of votes (\text{maxVotes}), the voting duration (\text{processDuration}), and the desired security level, which relates to the number of participating sequencers.
The total cost for a voting process is calculated using the formula:
\text{totalCost} = \text{baseCost} + \text{capacityCost} + \text{durationCost} + \text{securityCost}
Components of the Cost:
-
Base Cost: \text{baseCost} = \text{fixedCost} + \text{maxVotes} \cdot p, where \text{fixedCost} is a fixed fee, and p is a small linear factor.
-
Capacity Cost: \text{capacityCost} = k_1 \left( \frac{\text{totalVotingProcesses}}{\text{totalSequencers} - \text{usedSequencers} + \epsilon} \cdot \text{maxVotes} \right)^a, where k_1 is a scaling factor, a controls non-linearity, and \epsilon is a small number to prevent division by zero.
-
Duration Cost: \text{durationCost} = k_2 \cdot \text{processDuration}^b, with k_2 as a scaling factor and b controlling the scaling based on duration.
-
Security Cost: \text{securityCost} = k_3 \cdot e^{c \left( \frac{\text{numSequencers}}{\text{totalSequencers}} \right)^d}, where k_3 is a scaling factor, and c, d control the exponential scaling related to the number of sequencers used.
Sequencers earn rewards based on the number of votes processed and the number of vote rewrites (including re-encryptions for receipt-freeness). The total reward for a sequencer i is calculated as:
\text{sequencerReward}_i = R \left( \frac{\text{votes}_i}{\text{maxVotes}} \right) + W \left( \frac{\text{voteRewrites}_i}{\text{totalRewrites}} \right)
This is subject to the constraints:
\frac{\text{voteRewrites}_i}{\text{votes}_i} \leq T and R > W
Ensuring that sequencers prioritize processing new votes over rewrites. Here, R and W are parts of the reward pool allocated for processing votes and vote rewrites, respectively, and T is a predefined constant limiting the number of rewrites per vote.
Sequencers who fail to meet their obligations may have their collateral slashed, calculated as:
\text{SlashedAmount}_i = s \cdot \text{StakedCollateral}_i
where s is the slashing coefficient (0 \leq s \leq 1).
Resources
-
Full version of the whitepaper: https://whitepaper.vocdoni.io
-
List of repositories where the MVP version of the protocol is being implemented:
- Circom circuits for voter GitHub - vocdoni/z-ircuits: Vocdoni Z snark circuits.
- Sequencer crypto primitives GitHub - vocdoni/gnark-crypto-primitives: A set of custom circuits writted in Gnark that are required to support anonymous voting on Vocdoni.
- Circom to Gnark parser GitHub - vocdoni/circom2gnark: Circom to Gnark Groth16 parser and recursion example
- ElGamal and DKG sandbox: GitHub - vocdoni/vocdoni-z-sandbox
-
Contact: pau [at] vocdoni [dot] io
-
Discord: https://chat.vocdoni.io