Understanding the security properties of ZK proofs is a monumental challenge. Since we are building a universal-purpose zkVM (called zkMIPS, because it combines zero-knowledge proofs with the MIPS instruction set), it’s vital that we consider security within every line of code that we develop.
Complicating all of this is a more elemental question, one sits at the heart of blockchain technology, especially ZK proofs: How do we define security in the first place?
Vague descriptions are a threat to any rigorous security analysis. So when analyzing the security of a system, we should always ask some basic questions:
- What exactly is the setting?
- Which are the parties?
- Which components of the system are trusted?
- What are the exact data in question?
Beyond that, we must ask: What are the security properties we want to maintain? Is it confidentiality? Integrity? Correctness? Non-repudiation?
Below we address the first set of questions. We will address the second set of questions in Part 2 of this post, coming soon in this channel.
Question 1: About the setting
In the context of the ZKM whitepaper (published recently at ETHResearch), Zero Knowledge deals with a scenario of Verifiable Computation between two parties, called V (the Verifier) and P (the Prover).
Here, the Verifier has a few computational resources (the case of a simple wearable device, a smart lock, or Ethereum Layer 1), while the Prover represents a very large, very strong entity (a cluster of computers, or even the cloud itself).
In this setting, it is natural that the Verifier wishes to outsource a computation. Let’s say that the Verifier is asking the Prover to compute the result y of running program F on input x, as in y=F(x). However, the Verifier doesn’t trust the Prover, since the Prover could send a wrong result y’, while claiming it is correct, collect the money for the work done, and disappear.
Figure 1: V wants to outsource the computation of program F with input x.
To avoid this scenario, the Verifier and Prover agree to add a verification to the outsourced computation. In addition to the result y, the Prover is also going to provide a proof (called Z) that y is indeed the result of running program C on x.
Moreover, the Prover will be doing lots of extra computations to make sure that 1) this proof Z is short, and 2) that verification of the correctness of Z is a very efficient algorithm, meaning that even a Verifier with few resources can easily perform this check.
Various techniques exist for realizing this scenario of Verifiable Computation, starting historically with probabilistically checkable proofs (PCP) and, more recently, using SNARKs and STARKs. One trait that these techniques have in common that they transform a computation into a very high degree and complex polynomial, and that the Verifier only needs to perform simple verifications on this polynomial to be convinced that the Prover performed correctly.
So the overall setting is that the Prover wants to prove to the Verifier that it performed the computation correctly, i.e. that y=F(x). Observe that F, x, y are the inputs to the protocol, and are known to both the Prover and Verifier. Please make sure not to confuse the input to the program F, namely x, with the inputs to the protocol, namely C, x and y.
So if all these values are public, you may ask: What is the Prover’s secret? Or, using ZK terminology, what is the witness, i.e. the data that the prover owns which allows him to prove the correctness of his claim? In the context of Verifiable Computation, this witness consists of data proving that the Verifier actually performed the whole computation of F on input x resulting in y, usually called the execution trace T.
Figure 2: P proves to V that it computed F(x) correctly by showing it knows a corresponding execution trace, which leads to the answer y.
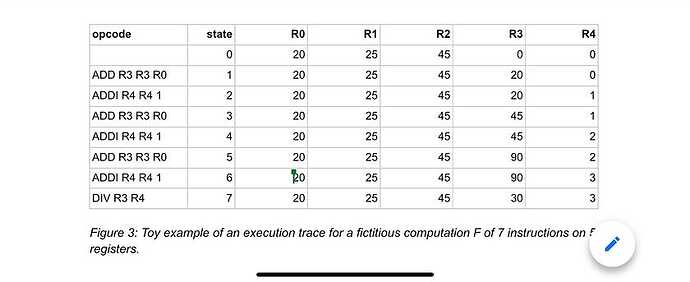
So what is an execution trace? Within the context of the zkVM that we are building, the computation happens in steps, and its overall state can be defined by the values of a finite list of variables. A valid computation is a sequence of states, from a well-defined initial state to some final state, in which each state transition represents a valid computation step.
It can be represented as a table whose columns represent the list of variables and whose rows represent each step of the computation. This table is known as the execution trace; the following diagram shows a toy example.
Check back soon for Part 2 of this post, where we will address the second set of questions, about the security properties we want to maintain in our zkVM, which we call zkMIPS.
Want to discuss this and other ZK-related topics with our core ZKM team? Join our Discord channel: discord.gg/Bck7hdGcns