3-Slot-Finality: SSF is not about "Single" Slot

[saltiniroberto]

3-Slot-Finality: SSF is not about “Single” Slot

Authors: Francesco D’Amato, Roberto Saltini, Thanh-Hai Tran, Luca Zanolini

TL;DR; In this post, we introduce 3-Slot Finality (3SF), a protocol designed to finalize blocks proposed by an honest proposer within 3 slots when network latency is bounded by a known value \Delta – even if subsequent proposers might be dishonest – while requiring only one voting phase per slot. This approach contrasts with previously proposed protocols for Single-Slot Finality, which require three voting phases per slot to finalize an honestly proposed block within a single slot resulting in longer slot time. We also show that 3SF guarantees all the key properties expected from SSF, offering an efficient and practical alternative that reduces overhead while ensuring fast and predictable block finalization within a few slots, and a shorter practical slot time (as voting phases take practically longer than other phases). As a result, our protocol achieves a shorter expected confirmation time compared to the previously proposed protocol, at the expense of a slight delay in block finalization, which extends to the time required to propose three additional blocks, rather than finalizing before the next block proposal. However, we believe that a shorter expected confirmation time could be sufficient for most users. Also, slot time is a crucial parameter affecting economic leakage in on-chain automated market makers (AMMs) due to arbitrage. Specifically, arbitrage profits – and consequently, liquidity providers’ (LP) losses – are proportional to the square root of slot time. Therefore, reducing slot time is highly desirable for financial applications on smart contract blockchains. Finally, we show that we can make a further trade-off: we can increase the number of voting phases to two, without this affecting the actual slot length, and achieve finalization in only two slots.

This post represents a summary of our extended technical paper that you can find here.

Observe that in this post, we will focus exclusively on the consensus protocol, setting aside the issues of validator set management. This aspect is independent of the design of an effective consensus protocol and can be addressed separately.

Single-Slot-Finality, or SSF, is a highly expected upgrade to the Ethereum consensus layer that is often associated with being able to finalize blocks within the same slot where they are proposed, a significant improvement over the current protocol, which finalizes blocks within 64 to 95 slots. This advancement would eliminate the trade-off between economic security and faster transaction confirmation.

However, do we really need Single-Slot-Finality?

To answer this question, let us take a step back and ask ourselves another question: What are the properties not guaranteed by the current protocol (Gasper) that we would like SSF to give us?

• Property 1. If the network latency is lower than a known value \Delta and \geq 2/3 of the validator set (by stake) is honest and actively participate, then a block proposed by an honest node is finalized in a short and predictable amount of time.
• Property 2. If the network latency is lower than \Delta and > 1/2 of the validator set (by stake) is honest, even though < 2/3 of the validators (by stake) are actively participating, blocks proposed by honest nodes will never leave the canonical chain and, once participation of honest validators is back up to \geq 2/3 (by stake), then such a block will be finalized within a short and predictable amount of time.
• Property 3. Using the same assumptions of the point above, there exists a way to confirm a block, that is, to determine whether such a block will always be part of the canonical chain and, consequentially, once participation of honest validators is back up to >= 2/3 (by stake), it will be finalized within a short and predictable amount of time.

As we can see, none of the properties listed above is necessarily about being able to finalize blocks within the same slot they are proposed. However, arguably, the sooner a block is finalized, the better. So, why don’t we just stick with Single-Slot-Finality given that we already have one such protocol (which, from here on, we refer to as SSF) that guarantees all of our desired properties above, including being able to finalize blocks within the same slot?

The reason is that SSF requires more than one voting phase per slot. The general issue with this is that, because of the large amount of data flooding the network when voting happens, in practice, extra latency must be accounted for each voting phase. For example, to reduce overall network bandwidth, Ethereum currently employs a signature aggregation scheme for each voting phase by which votes are first sent to aggregators who then distribute the aggregated signatures. This means that voting phases require 2\Delta time, that is, double the normal network latency. Even if in the future it is found that we can do away with aggregators, it is reasonable to expect that voting phases take longer than other phase. In the rest of this section, we assume that a voting phase lasts 2\Delta as per current Ethereum protocol.

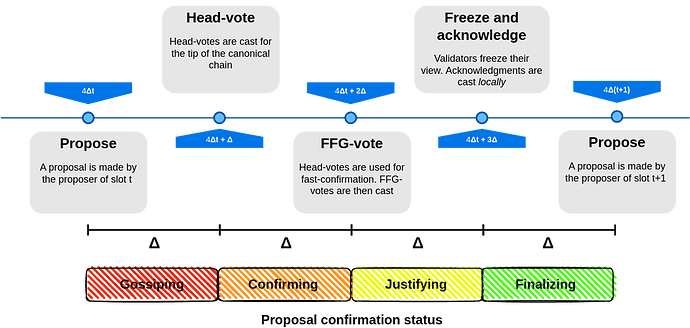
So, the more voting phases, the longer the block time tends to be. Specifically, as detailed later, SSF divides each slot in 4 phases: (1) block proposing, (2) Head-voting, (3) FFG-voting and (4) Acknowledgment voting plus view freezing (view-freezing is not important for the argument here). Phase (3) and (4) must wait for phases (2) and (3) to complete, respectively. However, the start of the next slot and any of its phases do not depend on phase (4). So, the slot length in SSF is \Delta + 2\Delta + 2\Delta + \Delta = 6 \Delta.

In our protocol (3SF) slots are also composed of 4 phases, but only one of them is a voting phase. Specifically, we have (1) block proposing, (2) Head/FFG-voting where both Head-votes and FFG-votes are cast, (3) fast-confirmation and (4) view-merging. Then, the slot length becomes \Delta + 2\Delta + \Delta + \Delta = 5\Delta.

First, block time has been shown to be an important parameter in determining the economic leakage of on-chain AMMs to arbitrage. For instance, arbitrage profits (and equivalently LP losses) are proportional to the square root of block time, so that a lower block time is very desirable by financial applications built on top of a smart contract blockchain.

Second, with a shorter block time, we can achieve a shorter expected confirmation time which is the expected delay from when a user submit a transaction to when such a transaction is confirmed, that is, to when it is included in a confirmed block. This corresponds to the time taken to confirm a block proposed by an honest proposer + \frac{(1+\beta) \cdot \text{slot-time}}{2(1 - \beta)} where \beta represents the adversarial power in the network. In both 3SF and SSF the time taken to confirm a block proposed by an honest validator is 3\Delta. So, for \beta = \frac{1}{3}, the expected confirmation time for SSF is 9\Delta whereas for our protocol is 8\Delta, meaning an \approx 11\% improvement. For \beta = 0, the expected confirmation time for SSF is 6\Delta whereas for our protocols is 5.5\Delta, meaning an \approx 8\% improvement.

However, as one would expect, while the expected confirmation time of 3SF is shorter, the expected finalization time (that is, the expected time take to finalize a transaction) is longer. The expected finalization time is computed similarly to the expected confirmation time, namely, the time taken to finalize a block proposed by an honest proposer + \frac{(1+\beta) \cdot \text{slot-time}}{2(1 - \beta)}. In SSF the time taken to finalize an honest block is 5\Delta, in 3SF is 11\Delta and the two-slot variant of 3SF is 8\Delta. So, for \beta = \frac{1}{3}, the expected finalization time for SSF is 11\Delta, for 3SF is 16\Delta, and for the two-slot variant of 3SF is 13\Delta, meaning that the expected finalization time for 3SF is \approx 46\% higher than that of SSF, but this reduces to \approx 18\% for its two-slot variant. For \beta = 0, the expected finalization time for SSF is 8\Delta, for 3SF is 13.5\Delta, and for the two-slot variant of 3SF is 10.5\Delta, meaning that the expected finalization time for 3SF is \approx 69\% higher than that of SSF, but this reduces to \approx 31\% for its two-slot variant.

Overall, 3SF achieves a balance by trading a higher expected finalization time for a shorter expected confirmation time, which could be sufficient for most users. At the same time, it offers shorter slot time. As additional benefit, the slot structure of 3SF more closely resemble the current Ethereum’s slot structure.

A previous research post already highlighted the issue about the number of voting phases in 3SF and put forward a solution for that. However, this solution could guarantee the desired properties only if the proposers in the two subsequent slots are also honest.

This takes a step in the right direction by reducing the protocol to only one voting phase per slot, but it also introduces a drawback: a lower probability of meeting the required conditions for finality. However, we now show that it is possible to design a protocol that can reduce the number of voting phase to one without requiring that proposers in subsequent slots are honest.

Recalling the SSF protocol

We build our 3SF protocol by using the SSF protocol as starting point, which is summarized by the following picture.

Let us now recall some of the most important concepts.
(The reader is however encouraged to read the original post.)

1. Ebb-and-flow construction. SSF consists of two sub-protocols. The first is a PBFT-style (name that comes from this seminal paper) sub-protocol that always ensures safety, even in the case of network partitioning, but it requires at least 2/3 honest stake. The second is the dynamically-available (DA) sub-protocol, which guarantees progress even if some honest validators stop participating, under the assumption of a simple honest majority. A protocol combining these two types of sub-protocols is referred to as an ebb-and-flow protocol.
2. Casper-based BFT sub-protocol. The PBFT-style sub-protocol is heavily based on Casper, the Finality Gadget currently used by Gasper. Compared to Gasper, in SSF checkpoints are pairs of blocks and slots, rather than blocks and epochs. This is because, in SSF, in some sense, epochs and slot are the same thing. However, the general rules for checkpoint justification and finalization are the same. Let us briefly recall such rules. First, block finalization is achieved through checkpoint finalization. Specifically, to finalize a block B, we need to finalize some checkpoint (B_\mathsf{d},s) where B_\mathsf{d} is a descendant of B and s \geq \mathsf{slot}(B_\mathsf{d}). Second, checkpoint finalization is achieved in two stages: first checkpoints are justified, then a justified checkpoint is finalized. Let us now explain how this process works. The genesis checkpoint (B_\mathsf{genesis},0) is by definition both justified and finalized. Justification and finalization of any other checkpoint is achieved through FFG-votes which are votes for links between checkpoints. They are of the form C_\mathsf{s} \to C_\mathsf{t}, where C_\mathsf{s} and C_\mathsf{t} are called the source and target checkpoints, respectively. A checkpoint (B,s) is justified if there are FFG-votes from \geq 2/3 of the validators (weighted by stake) for a link C_\mathsf{s} \to (B,s) where C_\mathsf{s} is a justified checkpoint. A checkpoint (B,s) is then finalized if (B,s) is justified and there are FFG-votes from \geq 2/3 of the validators (weighted by stake) for a link (B,s) \to (B',s+1) with B' descendant of B. In addition to this, in order to be able to finalize blocks within one slot, SSF introduces Acknowledgment votes ((B,s),s) that are, roughly speaking, a “compressed” FFG-vote saying that a validator saw a given checkpoint (B,s) justified at the end of slot s. Anyone who sees checkpoint (B,s) as justified and receives Acknowledgment votes ((B,s),s) from \geq 2/3 of the validators (weighted by stake) can safely consider checkpoint (B,s) finalized.
3. RLMD-GHOST as the DA sub-protocol. SSF leverages RLMD-GHOST as the DA sub-protocol to achieve Properties 2 and 3 above. In RLMD-GHOST, validators votes for blocks. We use the term Head-votes to refer to such votes. RLMD-GHOST works in the sleepy model where validators may fall asleep and stop participating for a period. A key property of RLMD-GHOST is that as long as the network latency is less than \Delta and less than 1/2 of the validators (weighted by stake) are dishonest, the block proposed by an honest proposer will receive and keep receiving the Head-votes of all active validators. Importantly, RLMD-GHOST comes with the following confirmation rule that allows determining whether a block is confirmed, that is, it will always be part of the canonical chain of any honest valiadator: Any block that is at least \kappa-deep with respect to the the current canonical chain is confirmed (the head of the canonical chain is 0-deep, its parent is 1-deep and so on). We refer to this rule as the \kappa-deep confirmation rule. The value \kappa represents the number of slots that we need in order to be sure, except for a negligible probability, that at least one of the proposers in these slots is honest. Clearly this means that \kappa >> 1.
4. Fast confirmation. Compared to the \kappa-deep confirmation rule, fast confirmation allows confirming a block within the same slot it has been proposed. However, it requires at least 2/3 of the validators (weighted by stake) to be honest and active. Fast confirmation of a block occurs when more than 2/3 of the Head-votes from all active validators (weighted by stake) are received after a time delay of \Delta from when they were sent. In the diagram above, the Head-votes are cast at 4$\Delta s$ + \Delta, meaning they are sent \Delta time within slot s. If by 4$\Delta s + 2\Delta$ an honest validator receives more than 2/3 of the Head-votes (weighted by stake) for a specific block B, then B is considered fast confirmed.
5. Integration between the BFT and DA protocols. In SSF, honest validators determine the FFG-vote to cast as follows. The source checkpoint corresponds to the greatest justified checkpoints in their view, which is the justified checkpoint with the highest slot (no two different justified checkpoints for the same slot can every be justified unless > 1/3 of the stake is slashed). The slot of the target checkpoint corresponds to the current slot while the block corresponds to the block fast confirmed by the DA protocol, if there exists one, or the highest block confirmed by the DA protocol via the \kappa-deep confirmation rule, otherwise.
6. Slots of length 4\Delta. Except when specifically stated, to align with previous literature, in the rest of this post, we assume that voting phases take just \Delta time, that is, we do not explicitly account for the extra latency introduced by voting phases. Then, in SSF, each slot has length 4\Delta.

Building our 3SF Protocol

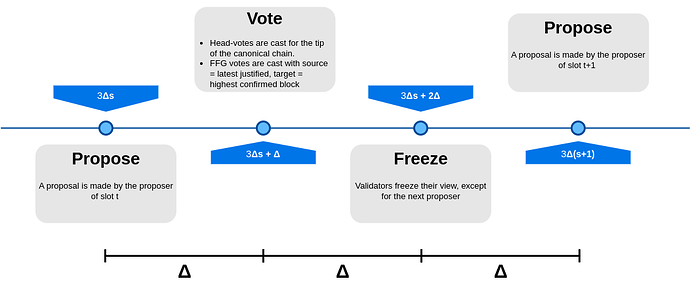
We now start building our 3SF protocol by taking the SSF protocol and applying the following modifications to have one single voting phase per slot.

1. FFG-votes are cast together with the Head-votes at \Delta time into a slot, where \Delta represents the network latency.
2. Remove fast-confirmations.
   Hence, the target of the FFG-votes is the longest chain confirmed by the DA protocol. Under this condition, the DA protocol ensures that if the proposer is honest, all honest validators see the same chain as confirmed by the DA protocol.
3. No Acknowledgment votes.

By removing one phase, the length of the slot then decreases to 3\Delta. The resulting protocol can be schematized as follows.

Let us now take a look at how a run of such a protocol would look like even under the simplifying assumption that we have two consecutive honest proposers and the usual assumptions that (i) < 1/3 of the validators (weighted by stake) are dishonest and the (ii) network delay is less than \Delta.

1. The proposer in slot s proposes block B.
2. Due to the DA protocol’s properties, all honest validators in slot s cast an Head-vote for B. However, given that B has just been proposed, B cannot also already be part of the chain confirmed by the DA protocol. This means that the FFG-votes sent by honest validators have as target a strict ancestor of B. All validators have the same view of the chain confirmed by the DA protocol. This means that they all send FFG-votes with the same target (B_\mathsf{a},s) with B_\mathsf{a} ancestor of B. (From now on, let us use the notation B_\mathsf{a} \preceq B to mean that B_\mathsf{a} is a non-strict ancestor of B, and B_\mathsf{a} \prec B to mean that it is a strict ancestor, that is, B_\mathsf{a} \preceq B means B_\mathsf{a} \prec B or B_\mathsf{a} = B.)
3. The proposer in slot s+1 proposes a block B' child of B and packs into it all the FFG-votes sent in slot s.
4. Validators voting in slot s+1, then see (B_\mathsf{a},s) as justified. This means that they cast an FFG-vote (B_\mathsf{a},s) \to (B'_\mathsf{a},s+1) (we use the notation C_\mathsf{s} \to C_\mathsf{t} to indicate an FFG-vote with source C_\mathsf{s} and target C_\mathsf{t}), where B'_\mathsf{a} \prec B'. However, given that we have dropped fast-confirmation, the DA protocol only confirms via the \kappa-deep confirmation rule. Given that \kappa > 1, this implies that B'_\mathsf{a} \prec B. As a consequence of this, we are at most able to justify a strict ancestor of B, not B, with the votes sent in this slot, which makes impossible to finalize B in the next slot.

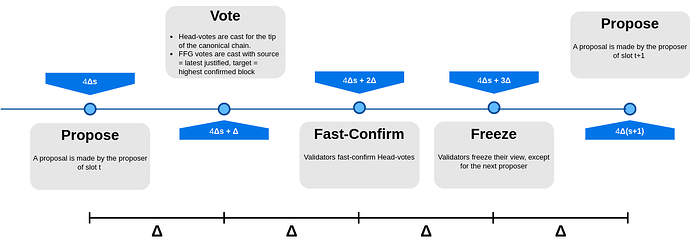
The above shows us that we do need fast-confirmations. Therefore, let’s reintroduce them into the protocol just presented. Specifically, for FFG-votes, we use the chain fast-confirmed in the previous slot, rather than the one from the current slot, to determine the target block. This is because, given that Head-votes and FFG-votes are cast at the same time, clearly we cannot use the Head-votes cast at a given slot to determine the target of the FFG-votes cast in the same slot. We just need to wait \Delta from the voting time to perform fast-confirmation. As a consequence of the above, we are back to a slot of length 4\Delta as shown by the following picture illustrating this last protocol.

Let us now take a look at whether this is going to work.

2. In slot s, the block in the target checkpoint of FFG-votes cast by honest validators is either the chain confirmed by the DA protocol (via the \kappa-deep rule mentioned above), or the chain fast-confirmed at the slot before. This turns out to be an issue as some validators may have fast-confirmed a block B^{\mathsf{fastconf}} in the slot before, some others might have not. So, it is very well possible that some validators cast an FFG-vote with target block B^{\mathsf{conf}}, others an FFG-vote with target block B^{\mathsf{fastconf}}_\mathsf{a}. The problem is that, even though B^{\mathsf{conf}}_\mathsf{a} \prec B^{\mathsf{fastconf}}, by using the justification rules of SSF/Gasper this leads to a situation where we do not justify any checkpoint for slot s, which seems like a step backwards rather then forward.

How do we fix this?

Note that when we finalize a checkpoint with block B, we finalize the entire chain, not only B. We could do the same for justified checkpoints. That is, if we justify (B,s) we also consider any checkpoint (B_\mathsf{a},s) where B_\mathsf{a} \preceq B as justified. However, this is not enough to address the issue highlighted from the last example, as different validators might FFG-vote for different checkpoints, even though the blocks included in such checkpoints are on the same chain.

We need to take this a step further:

An FFG-vote (B_\mathsf{s},s_\mathsf{s}) \to(B_\mathsf{t},s_\mathsf{t}), provided that the source checkpoint (B_\mathsf{s},s_\mathsf{s}) is justified, is considered contributing to the justification of any checkpoint (B',s_\mathsf{t}) where B_\mathsf{s}\preceq B' \preceq B_\mathsf{t},that is, B’ is any block between B_\mathsf{s} and B_\mathsf{t} included. Note that the slot in the target checkpoint and the justified checkpoint are the same.
If we have FFG-votes from \geq 2/3 of the validators (weighted by stake) contributing to the justification of (B',s_\mathsf{t}), then (B',s_\mathsf{t}) is considered justified.

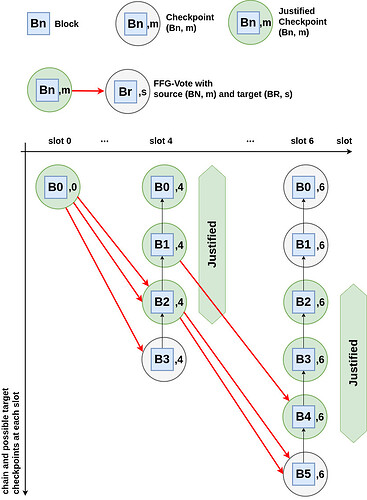
Before proceeding, let us go over the example below to ensure that this new justification rule is clear. We consider 3 slots, slot 0, 4, and 6. For each of these slots, say s, the Figure below shows the list of possible target checkpoints for FFG-votes cast in slot s. This includes all the checkpoints comprising any of the blocks received up to the voting time in slot s, except for the block proposed in slot s, paired with slot s.

We assume just 4 validators, all with the same stake.
Let us consider first the FFG-votes between (B0,0) and checkpoints for slot 4. If we take B to be such that B0 \preceq B \preceq B2, then we have 3 \geq \frac{2}{3} 4 FFG-votes between (B0,0) and a checkpoint (B_\mathsf{d},4) such that B \preceq B_\mathsf{d}.
Given that B0 \preceq B, as per our rule, (B0,4), (B1,4) and (B2,4) are justified. However, (B3,4) is not justified as only the FFG-vote (B0,0) \to (B3,4) is in support of its justification.
Now we move to the FFG-votes between checkpoints for slot 4 and checkpoints for slot 6. Note that by the reasoning above all of these FFG-votes have a justified checkpoint as source. Now, take B to be such that B2 \preceq B \preceq B4. Note that we have 3 FFG-votes between a justified checkpoint (B_\mathsf{a},4) and a checkpoint (B_\mathsf{d}.6) such that B_\mathsf{a}\preceq B\preceq B_\mathsf{d}. As per our rule, this means that (B2,6), (B3,6), and (B4,6) are justified. Importantly, (B0,6) and (B1,6) are not justified, despite (B0,4) and (B1,4) being justified. For (B1,6), this is because we only have the two FFG-votes (B1,4) \to (B4,6) in support of its justification. Whereas, for (B0,6) we have no FFG-vote is support of its justification.

This new rule clearly allows having more than one justified checkpoint for a given slot. This is OK, as they would be on the same chain. However, when computing the best justified checkpoint, using the checkpoint slot is not sufficient anymore. Then, we naturally define the ordering between checkpoints that have the same slot number to be according to the block’s proposed slot so that if \mathsf{slot}(B) < \mathsf{slot}(B'), then (\mathsf{slot}(B'),s) is greater than (\mathsf{slot}(B),s).

Then, let’s resume the previous example with this new protocol assuming that only the proposer of slot s is honest (in addition to the usual assumptions):

2. In slot s, any honest validator cast an FFG-vote C_\mathsf{s} = (B_{\mathsf{aa}},s') \to C_d = (B_\mathsf{a},s), with C_\mathsf{s} and C_d potentially different for each validator, but with the property that B_\mathsf{aa} \preceq B_\mathsf{a} \prec B. This set of FFG-votes then leads to justifying at least a checkpoint (B_\mathsf{j},s) with B_\mathsf{j} \prec B.
   Also, all honest validators fast-confirm B.
3. The proposer of slot s+1 can propose whatever they want, or nothing at all.
4. In slot s+1, any honest validator casts an FFG-vote (B_\mathsf{j},s) \to (B,s+1), where B_\mathsf{j} can be potentially different for each validator, but B_\mathsf{j} \prec B. This is because, from the point above, we know that there is at least a justified checkpoint for slot s. Overall, this means that this set of FFG-votes justifies (B,s+1). So far so good! It looks like we are headed in the right direction!
5. The proposer of slot s+2 can propose whatever they want, or nothing at all.
6. Given the rules on checkpoint ordering that we have established above, any honest validator sees (B,s+1) as the greatest justified checkpoint. Then, any honest validator cast an FFG-vote (B,s+1) \to (B'',s+2) where B'' can be potentially different for each validator, but, due to the DA protocol’s properties, B \prec B''. Using the Gasper/SSF finalization-rule this would not necessarily yield the finalization (B,s+1). However, this can be easily fixed. Let’s see how!

Note that in Gasper/SSF, in an FFG-vote (B,s+1) \to (B',s+2), block B' doesn’t carry any meaningful information about whether it is safe to finalize (B, s+1). Such a vote is saying that the validator signing it saw (B,s+1) as the greatest justified checkpoint by the time they vote in slot s+2 (which is exactly what an Acknowledgment vote does in the SSF protocol). Hence, such a validator would then be slashed if it in a later slot (that is, in a slot > s + 2) it signs an FFG-vote with source a checkpoint lower than (B,s+1). This means that we can modify the finalization rule as follows.

If we have \geq 2/3 of the validators (weighted by stake) FFG-voting (B,s+1) \to (B',s+2), with B' potentially different for each validator, but such that B \preceq B', then (B,s+1) is finalized.

With this last modification, at step 6 above, we finalize block B as we were hoping to do!

Is this protocol safe?

Fair question! In order to make this protocol safe we only need to slightly modify the slashing rules.

Let us start by recalling the slashing rules employed by Gasper which are the same used by SSF (to be precise SSF has an additional rule that uses for Acknowledgment votes, but we can ignore it as we do not use that type of vote).
First, a validator is slashed if it sends two different FFG-votes but with target checkpoints for the same slot.
Second, a validator is slashed if it sends two FFG-votes (*,\mathit{s1}_\mathsf{s})\to(*,\mathit{s1}_\mathsf{t}) and (*,\mathit{s2}_\mathsf{s})\to(*,\mathit{s2}_\mathsf{t}) such that \mathit{s1}_\mathsf{s} < \mathit{s2}_\mathsf{s} and \mathit{s2}_\mathsf{t} < \mathit{s1}_\mathsf{t}. This is called a surround vote as the first vote surrounds the second one.
Gasper/SSF ensures that if two conflicting blocks are finalized, then we can slash at least 1/3 of the validator set.

We now show that the two rules above are not sufficient for 3SF.
Note that in Gasper/SSF, it is perfectly legal for a validator to cast two FFG-votes with source checkpoints from the same slot. This fine as Gasper/SSF ensures that no two different checkpoints for the same slot can ever be justified (unless > 1/3 of the validators, weighted by stake, are dishonest). However, with our modified protocol, this is not true any more. This means that in our protocol, it is currently possible to cast two FFG-votes (B,s) \to (B_d,s+1) and (B_\mathsf{a},s) \to (B',s+2), where both (B,s) and (B_\mathsf{a},s) are justified, with B_\mathsf{a} \preceq B, and B' conflicting with B_d. This means that the first FFG-vote can contribute to finalizing checkpoint (B,s) and the second one to justifying the higher, but conflicting checkpoint, (B',s+2) from which then it is possible to finalize such a checkpoint without committing any slashsable offense.

Fortunately, the fix to this issue is straightforward. We extend the Gasper/FFG slashing rules with the following one.

Two FFG-votes (\mathit{B1},s) \to (*,\mathit{s1}_\mathsf{t}) and (\mathit{B2},s) \to (*,\mathit{s2}_\mathsf{t}) with \mathsf{slot}(\mathit{B1}) < \mathsf{slot}(\mathit{B2}) and \mathit{s2}_\mathsf{t} < \mathit{s1}_\mathsf{t} constitutes a slashable offense (surrounding vote).

As we can see, with this rule, the situation described above is prevented.

Implementation Considerations

The newly introduced slashing rule requires accessing the block’s slot number. This poses a slight problem as checkpoint FFG-votes do not include the full block, but only the hash and we need to be able to determine validators’ slashability just by looking at the FFG-votes that they cast, without needing to have received the actual blocks that the refer to via their hashes.

This is easily solved by extending checkpoint to be triples (H,s,p), rather than just tuples (H,s), where H is the hash of a block (say B), s is the checkpoint’s slot and p is B's block slot, that is, p = \mathsf{slot}(B). Naturally, this also means that before accepting an FFG-vote (H,s,p) \to C_\mathsf{t} as valid and accounting it for justifications/finalizations, we need to check that B.\mathsf{slot}=p, where B is the block with hash H.

What about the other properties?

So far, we have just addressed the first property of our interest: If the network latency is lower than \Delta and >= 2/3 of the validator set (by stake) is honest and actively participate, then a block proposed by an honest node is finalized in a short and predictable amount of time.

What about the other two properties that we have listed at the beginning?

Those properties are already guaranteed by the DA protocol employed by SSF, namely RLMD-GHOST. So, we can either use RLMD-GHOST as our DA protocol or another DA protocol, like TOB-SVD.

In our extended technical report, we show in detail how both RLMD-GHOST and TOB-SVD can be used to achieve 3-Single-Slot Finality following the description we just presented.

Can we do better than 3-Slot-Finality?

It turns our that we can actually reduce finalization to just two slots by re-introducing Acknowledgment votes.
Of course, this mean two voting phases per slot, rather than one, but, as discussed above, this does not impact the actual slot length (that is, when we consider the extra latency required by voting phases), as the distribution of Acknowledgment votes can proceed in parallel to any subsequent phase.

In 3SF, Acknowledgment votes would be cast at the fast confirmation time, that is, at 2\Delta in a slot.
As in the SSF protocol, to keep things safe, we would need to add the following slashing rule.

An FFG-vote (\mathit{B1},s1_\mathsf{s}) \to (*,s1_\mathsf{t}) and an Acknowledgment vote ((\mathit{B2},\mathit{sa}),\mathit{sa}) with \mathit{sa} < s1_\mathsf{t} and either s1_\mathsf{s} < \mathit{sa}, or s1_\mathsf{s} = \mathit{sa} and \mathsf{slot}(\mathit{B1}) < \mathsf{slot}(\mathit{B2}) constitutes a slashable offense.

[jannikluhn]

How should Δ be chosen and would it make sense to adjust it dynamically based on the recent confirmation failure rate?