As seen in this previous ethresearch post and in this paper, one way to get an SSF protocol is to modify RLMD-GHOST (a slight variant of LMD-GHOST) by adding one round to it. This allows for fast confirmation of proposals, and in turn for FFG votes to be immediately cast with the block proposed in the current slot as a target, so that we can justify a proposal within its proposal slot (and optionally we can also finalize it immediately with one more round of votes, if desired).
This is done not only for the sake of finalizing as fast as possible, but also because this way we can fully benefit from the view synchronization brought about by an honest proposer: an honest proposer can ensure that all honest voters have the same source, the latest justified in its view, and moreover that they also have the same target, which is precisely its proposal, as it is immediately fast confirmed by all. Since every honest voter shares the same source and target, a justification of the target can be ensured, and this makes the protocol reorg resilient even when there exist a justification which is known only to the adversary and which conflicts with the canonical chain, as might happen after a period of asynchrony. Even if that is the case, an honest proposer can ensure a new justification, which is the latest and thus overrides any adversarially held one. In essence, this prevents bouncing attacks.
As it turns out, we can exploit this synchronization to ensure reorg resilience even without the ability to fast confirm a proposal immediately. While doing this means giving up the ability to justify and finalize a block within its proposal slot, it can be a worthwhile tradeoff because we can entirely remove the fast confirmation and FFG voting phase of a slot, and instead casting FFG votes together with head votes. In other words, we can obtain a streamlined protocol, with a single proposal and voting phase per slot.This is particularly beneficial because voting phases are expensive both in terms of time and bandwidth, when the validator set is large. The key to this change is to use a different kind of confirmation, which we are going to refer to as strong confirmation. As we will see, not only strong confirmation gives us security guarantees which are in some way superior, but also is transferable, meaning that there exist a notion of confirmation certificate, a piece of evidence which can be shared to get all validators to agree that a block is confirmed. Contrast this with fast confirmation, where confirming something or not depends on when a certain set of votes is observed, not only on the votes themselves.
Strong confirmation
Definition
Let a slot n \delta-quorum for block B be a set votes from slot n, from unique senders having total stake \geq \delta > 1/2, all voting for a descendant of B.
We say that a block B is strongly \delta-confirmed, if for some n we have the following \delta-certificate:
- A slot n \delta-quorum for B, with a set of senders S
- A block B' proposed at slot n+1 which contains the \delta-quorum
- A slot n+1 \delta-quorum for B' with set of senders S' = S.
We refer to S as a \delta-clique.
Security guarantees
The name is due to the fact that, while slightly slower than the fast confirmation used in the SSF paper, strong confirmation gives stronger guarantees. In fact, this notion confirmation corresponds to the notion of finality in LMD-GHOST, which is accountably safe. Here, that is not the case, because we are using RLMD-GHOST, i.e. using an expiration period \eta for messages, which rules out any asynchronous safety. Crucially, this is only for periods of asynchrony longer than the expiration period. Strong \delta-confirmation gives the following guarantees:
- Unless \delta - 1/2 of the stake is identified to have violated the voting rules (which can be made slashable), B will remain in the canonical chain in slots [n+1, n+\eta], even if the network is asynchronous in them. If moreover there is an honest majority and the network is synchronous at least once every \eta slots, B remains in the canonical chain forever.
- If there is an honest majority, and the network if synchronous in slot n, n+1 and n+2 and at least once every \eta slots afterwards, B will remain in the canonical chain forever, unless \delta - 1/2 of the stake equivocates in slots n or n+1.
Note that the second property makes the additional assumption of synchrony during slot n, n+1 and n+2, giving us a small additional guarantee, namely that a safety violation then necessitates equivocations, rather than a different kind of (here yet unspecified) violation of the voting rule. The latter is still attributable and can still be made slashable, but attribution requires an online process, rather than simply observing slashable evidence, as is the case for equivocations
In RLMD-GHOST, \delta can be freely chosen by anyone that wants to confirm blocks, trading off liveness and safety. On the other hand, when using RLMD-GHOST as a building block for an ebb-and-flow protocol (available chain + finality gadget), we additionally treat \delta as a protocol parameter, because we need all validators to agree on a notion of confirmation, as confirmation is a prerequisite for finality. We would then set \delta = \frac{2}{3}, to match the finality threshold. This means that, as long as \frac{2}{3} of the stake is honest and online, we can both (strongly) confirm blocks in this way and justify/finalize them, so that liveness of the final protocol does not need extra assumptions.
The fast confirmation in RLMD-GHOST similarly requires a threshold of \frac{2}{3}, so it has the same liveness as this rule, and it has the following guarantee, similar to the second one for strong confirmation:
Unless \frac{1}{3} of the stake equivocates in slots n, and if the network if synchronous in slots n and n+1 and least once every \eta slots afterwards, then B will remain in the canonical chain forever.
Note that this is a bit stronger than the guarantee we had before, because a safety violation under synchrony requires \frac{1}{3} slashing for equivocations rather than \frac{2}{3} - \frac{1}{2} = \frac{1}{6}, which is what we get for strong confirmation when we set \delta = \frac{2}{3} to have liveness resilience of \frac{1}{3}. On the other hand, we do not have an equivalent of the first guarantee of strong confirmation, so we are entirely reliant on synchrony and honest majority: if synchrony does not hold at slot n, the confirmation can be broken, and if we do not have an honest majority then the confirmation can be broken immediately at slot n+1, without any slashing required. Contrary to this, while strong confirmation does eventually rely on synchrony and honest majority as well (due to the existence of the expiration period) there is an initial period of \eta slots in which a reorg cannot happen except with \delta - 1/2 of the stake being slashable.
Protocol with finality
In the full protocol with fast finality, we are only going to always consider the latest justified to be strongly confirmed, and we are going to consider any canonical descendant of it strongly confirmed if there is a \frac{2}{3}-certificate for it. This way, there is always a highest confirmed block, and it is always canonical and a descendant from the latest justified, which makes it a perfect target for justification.
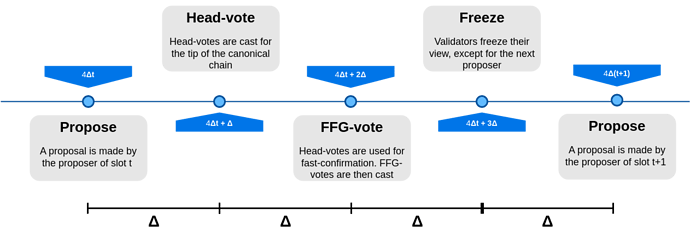
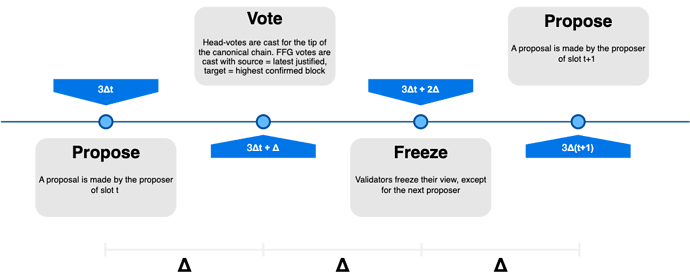
The fork-choice is the same two-step fork-choice as in the SSF paper, i.e., start from the latest justified and run RLMD-GHOST. A slot of the final protocol works this way:
- Propose: the proposer broadcasts a block extending the head of the chain, and a view-merge message with its view
- Vote: everyone merges their frozen view with the proposed view, if applicable, and broadcasts a head vote for the head of the chain and an FFG vote whose source is the latest justified and whose target is the highest confirmed block
- Freeze: everyone except the next proposer freezes their view
Behavior
Crucially, the proposer is able to synchronize the honest voters’ views on three things:
- The latest justified checkpoint
- The head of the chain
- The highest confirmed block
For the latter, they simple have to include the highest \delta-certificate they know for a canonical descendant of the latest justified, if there is one. All views that agree on these three things will produce the same head vote and the same FFG vote, and this is essentially all we need to ensure all good properties of the protocol. In particular, we have the following after \max(GST, GAT), i.e., at a point when all honest validators are always online and the network is always synchronous:
Reorg-resilience: a block proposed by an honest proposer never leaves the canonical chain
Proof: Say B is proposed by an honest proposer at slot n. All honest validators at slot n vote for B, and moreover they all make the same FFG vote C_1 \to C_2, where checkpoint C_2 = (A, n), for A the highest confirmed block, which is canonical and thus an ancestor of B. Therefore, C_2 is justified, and in particular becomes the latest justified. Since all honest head votes from slot n were for B, and the latest justified is now an ancestor of B, the fork-choice at slot n+1 outputs B as the head of the chain, and thus all votes from honest validators are again for (a descendant of) B. Moreover, no justification from this slot can conflict with B. We can continue by induction, establishing that B is always canonical in all future slots.
Liveness of justifications: If slots n,n+1 have honest proposers, then block B proposed at slot n is strongly confirmed in slot n+1 and justified in slot n+2
Proof: As in the previous proof, B receives all honest votes at slot n, which form a 2/3-quorum. Moreover, B is always canonical in all following slots. The proposer of slot n+1 includes the 2/3-quorum in its proposal B', and again by the previous proof B' receives all honest votes at slot n+1, so B becomes strongly confirmed, and in particular the highest confirmed block. Also, at slot n+1 some checkpoint C is justified, since all honest validators make the same FFG vote, and becomes the latest justified for everyone. At slot n+2, all honest validators then see C as the latest justified and B as the highest confirmed block, so their FFG votes are all for C \to (B,n+2), and (B,n+2) is justified.