APS-burn in the context of a Decentralized L2
Overview
We propose a design for Attester-Proposer-Separation that is tailored for the context of a decentralized L2. This design is intended to operate in the context of an L2 with its own validator set, running some sort of BFT consensus protocol, with single slot finality.
This design is based on the APS-burn design from @barnabe, but with some notable differences. It assumes that there are short block times, preferably one second, and no longer than 2 seconds, and that each block is final within the scope of the canonical L2 chain (prior to being finalized on L1) . This design aims to obtain the benefits of APS in an L2 context, while aiming to mitigate censorship, and mitigate the negative externalities of multi-block MEV. These properties are achieved using a sealed-bid auction, similar in principle to the Sealed execution auction proposal from Anders, but in an L2 context.
To understand the motivation behind this design, as well as its trade-offs, see the “benefits” and “risks” sections below.
DO NOT read this post if:
- You are trying to keep up with the important developments in Ethereum and attempting to determine which posts are important and which aren’t. This post is intended for soliciting early feedback on a design that is specific to decentralized rollups, and is not a finalized proposal.
DO read this post if:
- You are trying to decentralize a rollup, and are considering adopting an PoS consensus protocol, and are interested in exploring ideas within the design space.
Related Reading
- More pictures about proposers and builders - Barnabé Monnot
- Censorship Resistance in On-Chain Auctions - Elijah Fox, Mallesh Pai, Max Resnick
- Sealed execution auction - Anders Elowsson
- On block-space distribution mechanisms - Mike Neuder
- Block vs. Slot Auction PBS - Julian Ma
MEV Burn related reading:
- MEV burn—a simple design
- The price is right: Realigning proposer-builder incentives with predictive MEV-burn
- Dr. changestuff or: how i learned to stop worrying and love mev-burn
- In a post MEV-Burn world - Some simulations and stats
Description
We propose a method whereby the right to propose a future block is obtained via an on-chain auction.
For every slot n, the auction for block proposal rights starts at slot n - t and runs for k slots. The auction closes at slot (n - t) + k. During the period between n - t and (n - t) + k, bids are submitted to an on-chain smart contract. Each bid specifies an amount of some defined token that will be burned as part of the block that will be proposed at slot n. The winning bid is the bid that burns the most tokens.
During the auction between slot n - t and (n - t) + k, bids are posted on-chain as sealed commitments. After the auction closes at slot k, there is a buffer period of b blocks in which no new bids are accepted by the smart contract for slot n. After this buffer period, and up to slot n, bidders post their opened commitments, which reveal the amount they are bidding. The block that is proposed to the network at slot n, must be from the same address specified in the highest bid in the auction for slot n, and also burn the amount of tokens specified in the bid.
Each bid is composed of the height of the slot being bidded on, the address that will propose the block, and an amount of MEV that will be burned in the block.
Mitigating multi-block MEV
By incorporating a sealed bid auction, we can mitigate concerns around multi-block MEV. One of the main concerns with various APS designs is that it allows bidders to bid on block proposal rights for a contiguous segment of slots. If a bidder knows that they have the rights to slot n, then they can bid higher than anyone else for slot n+1, because they know that they can employ lucrative multi-block MEV strategies such as censoring price oracle updates or censoring sell orders on a trading pair to drive up the price etc.
In order to mitigate this concern, it is imperative that the bidders have no guarantee of having won the auction for slot n while the auction for slot n+1 is open.
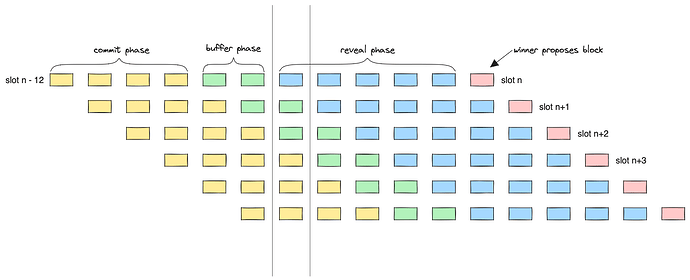
As an illustrative example, consider the following instantiation where bidders bid for the right to propose a block 12 slots in the future (t = 12), and they have 4 slots in which to submit bids (k = 4), followed by a buffer phase in which the on-chain auction will not accept bids (b = 2) followed by the reveal phase.
As you can see from the following visualization, is we assume that all bids for the slot n auction are revealed at slot (n - t) + k + b then the bidder for slot n only finds out that they have won block proposal rights for slot n after the auction for slot n+1 and slot n+2 have already closed.
Censorship
Censorship is a concern with any on-chain auction (ref: Censorship Resistance in On-Chain Auctions). Obviously block builders are highly incentivized to censor any transactions to the on-chain auction that that carry bids that aren’t their own, which means that the only bids that will make it to the on-chain contract are from block builders that already have proposal rights to slots, as these builders will likely only include their own transactions to the auction contract.
The only way to fully mitigate censorship is through some form of inclusion lists, or a design that facilitates multiple concurrent block proposers. We propose that this sort of mechanism is an integral part of this design, but the exact details of the mechanism employed are out of scope for this piece.
However, even without an inclusion list / MCP mechanism, censorship of auction transactions becomes prohibitively expensive quite quickly. This is because every transaction that is censored has associated transaction fees that can be collected by some other block builder, which they can use to increase their bids with. The censoring block builder will therefore incur a competitive disadvantage for every bid they censor. Moreover, the censoring block builder will incur the cost of each bid they censor for every block they propose, resulting in a linear increase in cost over time. In other words, If n blocks are proposed, and k transactions are censored per block, the total cost incurred by the censoring block builder becomes:
CoC=n\times\sum_{i=1}^{k}C_{i}
Collateralization and Penalties
This design requires that bidders are collateralized in order to submit bids, and that this collateral is slashed under certain circumstances:
- If bid commitments are not revealed, this can incur penalties. The reason for this is to prevent bidders from submitting multiple bids and then just revealing them conditionally based on what other bidders reveal (as detailed in this paper - h/t @quintuskilbourn for this). Obviously censorship resistance is important in order to prevent these penalties from being used for griefing attacks.
- If the winner of an auction for slot n, does not propose a block for slot n, they are slashed.
- If the winner of an auction for slot n, equivocates and proposes more than one block for slot n, they are slashed.
- If the proposed block is valid, and is from the auction winner, but does not burn the amount of MEV that was stipulated in the winning bid, the collateral is slashed.
There are two ways to approach collateralization:
1 | Per-Bidder-Collateralization
This requires that a block builders / bidders posts some collateral on-chain, and that this will be subject to slashing conditions. Once the collateral is posted, the bidder can participate in any number of auctions and submit any number of bids. The collateral can be withdrawn at any stage, but is subject to some defined delay period.
2 | Per-Bid-Bonding
Bidders do not need to be collateralized, but each individual bid will require a bond. In the case of the winning bid, the bond is returned when the block for the slot is delivered. In the case of not winning the bid, the bond is returned only if the bid commitment was revealed.
As a side note: per-bid-bonding can also potentially be used to prevent bids being revealed earlier through some side-channel, by allowing anyone to cancel their bid before the auction closes and withdraw their bond if they reveal the pre-image. Once the auction is closed, then only the original bidder can withdraw the bond.
There are subtle trade-offs between the two approaches:
-
Per-bid-bonding could potentially be more centralizing, as it favors better capitalized bidders. With a slot n+t auction with a per-bid bond of S, then bidders will need t \times S to participate in every auction.
-
On the other hand, this potentially improves censorship resistance to a degree, as the same bidder can bid from different addresses, reducing the scope for targeted censorship of specific rival block builders.
Preventing bids from being revealed early
It’s not entirely clear what the incentives would be for bidders to reveal their bids early, but the effect of revealing bids early will undermine the value of a sealed-bid auction, and will allow for multi-block MEV strategies to be employed. We can imagine a scenario whereby somebody constructs a mechanism employing ZKPs to allow bidders to reveal their bids, in order to understand if their bid is lower than another bid, which would give them the option to bid higher. This could be a useful tool for participants in the auction.
To mitigate against the risks of bidders revealing their bids early, it should be impossible, or very hard, to prove what the bid was. There are a number of ways of accomplishing this:
Using threshold encryption
The validators will use distributed-key-generation (DKG) to create a threshold encryption key, which is part of the headers for every block. The BFT round leader will also be responsible for collecting the keys from validators, posting the encryption key, and also gossipping the decryption key at the right time, so that it can also be included in the block headers. This will allow bidders to encrypt their bids when they are posted on-chain. It will also allow them to decrypt their bids locally to ascertain if they have won the block proposal rights for slot n. At this stage it should be deterministically known to all parties who have won the slot n auction.
Upon receiving a new block for slot n, validators will examine the amount of MEV burned in the block as well as the address of the proposer. They will take these two pieces of data and encrypt them using the threshold encryption key for the auction for slot n. If there is a bid that exactly matches the ciphertext, and that bid is from the proposer that is proposing the block, and is correctly collateralized, and most importantly, if there is no higher bid in the auction, then that block is accepted. This construction can be strengthened by imposing slashing conditions on entities that propose blocks that do not have a winning bid associated with it.
The benefit of this approach is that it precludes any possibility of revealing bids early, assuming an honest majority of validators. However, it does add some extra complexity to the consensus layer, as well as the overhead of establishing clear and reliable public transmission of threshold encryption keys.
Using a Verifiable Delay Function
In order to reveal a commitment, the smart contract must verify an accompanying Verifiable Delay Function (VDF) proof. The VDF ensures that any bid must take at least d seconds to produce a proof for. While there is nothing to stop bidders revealing their bids, it makes it difficult for bidders to prove what they bid, as the proof will take approximately d seconds to produce.
There are multiple VDF schemes that can be employed. Such a scheme was proposed by Nomadic Labs (see Timed Commitments Revisited).
Note that in this scheme, the commit binding is deterministic, so not completely resilient to revealing bids. In the specific scheme, if the bidder shares the values used to generate the commitment (i.e., G, g, e, k, and ct), others can reproduce the commitment \psi, thereby revealing the bid. Further work is needed to understand the complexity involved in doing this in a ZKP, in order to understand whether the complexity is sufficient to discourage revealing of bids. If needed, we would change the scheme to use a key derivation function that is suboptimal for use within zk circuits, resulting in inefficient proof generation, and therefore a similar level of effort required to create the actual VDF proof.
Note that while it is possible to just use VDFs by themselves without the complexity of a commit-reveal scheme, this has the drawback of allowing bidders to produce multiple VDFs concurrently in order to retain the option of conditional bidding.
Risks / Concerns
Reduced Competitiveness in Bidding
Bids are a bet on averages, this can potentially have more centralizing effects than a JIT block auction, because it precludes any opportunistic MEV strategies that capitalize on MEV spikes, which could prevent block builders that exist on these strategies from participating. Also, because it is a bet on averages, the system may favor the most well capitalized block builders.
Also, because we are using a sealed-bid auction, participants are not bidding in response to each other’s bids. This removes the natural competitiveness that drives up prices, and so the overall level of bidding is likely to be somewhat lower.
L2 reorg resistance
This design assumes a BFT consensus protocol with single-slot-finality, wherein reorgs do not occur in the normal case. If reorgs are a concern, one can adapt the above design to include a second buffer phase at the end of the reveal phase but before slot n. This would force any incentivized reorg to be at least as deep as the size of the second buffer phase, making it much more expensive, and so disincentivizing malicious reorgs.
Benefits
The benefit of APS is that there is no longer a requirement for mev-boost relays
The reason is that there is no negotiation between proposers and relayers (in terms of the proposer being the BFT round leader, who proposes blocks to the validator set). In the mev-boost scenario, the relayers are required in order to give some assurance to the builder that the proposer will not unbundle their block and steal the MEV, and also to give assurance to the proposer that the builder will in fact release the block on time, and not cause the proposer to get slashed. This is necessary to maintain PBS (unless ePBS is implemented), without which searcher bots will engage in PGAs which will cause significant and adverse network congestion.
It reduces the centralizing effects of MEV on the validator set
While mev-boost already does this in terms of democratizing access to MEV, there are still some centralizing effects from having MEV flowing to validators. For example, co-locating validator nodes close to relays means that validators can benefit from reduced latency and the higher bids that emerge in the final milliseconds of the slot. This latency advantage has compelling economies of scale for larger staking pools, which drives both economic and geographic centralization.
Strengthens PoS tokenomic design
For L2s that maintain their own gas token, APS simplifies the modeling of token rewards and penalties with regards to the validator set. This is because MEV no longer flows to the validators, which makes the validator risk/reward profile more deterministic and easier to reason about. Validators will just receive rewards as designed by the protocol and nothing more, which makes it easier to design PoS tokenomics. APS-burn also acts as a natural token sink, strengthening the tokenomics by having a deflationary effect on the token itself.
Future Work
As well as soliciting early feedback and peer review, we plan to work on determining how best to model this design so that we can understand the trade-offs in the design choices such as threshold encryption or VDFs, parameterization of the on-chain auction, per-bidder-collateralization or per-bid-bonding, and to understand the extent to which we can confidently predict the behavior of participants.