Analysis on ''Correlated Attestation Penalties''

Economics
1

Analysis on ‘‘Correlated Attestation Penalties’’

This is a quick quantitative analysis on anti-correlation penalties looking into its potential impact on staking operators and CL clients. Before getting into it, make sure to check out Vitalik’s recent proposal on anti-correlation incentives in his latest blog post.

Anti-correlation Penalties

In the current landscape, stakers benefit from economies of scale: enhanced network connectivity, superior hardware reliability, and the expertise of devs managing the infra all improve with scale. Consequently, economies of scale act as a strong force towards centralization within blockchain networks.

To strengthen decentralization, it is essential to architect mechanisms that counteract the advantages of economies of scale.

Fortunately, economies of scale are intrinsically linked with correlation effects: When a single operator runs many validators on one machine and experiences downtime, all those validators are affected at once. Thus, leveraging economies of scale comes with correlation effects. This results in a correlated risk and anti-correlation penalties punish those who leverage economies of scale to their advantage.

In this context, the distinction between “anti-correlation incentives” and “correlation penalties” is minimal, as both strategies aim towards the same objective of promoting decentralization.

It is important to note that the beacon chain lacks awareness of validator clusters. It perceives only individual validators, which appear largely indistinguishable from one another. Hence, anti-correlation incentives target the “hidden” connections among validators. While not guaranteeing improved decentralization in every instance, anti-correlation penalties may contribute positively to the broader objective of reducing centralization forces.

Vitalik’s initial proposal

The initial proposal introduces the formula p[i] = \frac{misses[i]}{\sum_{j=i-32}^{i-1} misses[j]} and caps it at p = 4.

This means, to determine the penalties of a specific slot, we maintain a moving average on the number of missed attestations over 32 slots and then compare it with the number of missed attestations for the current slot. In the case that the number of missed attestations in a slot is higher than the moving average, p > 1, a correlated penalty is applied.

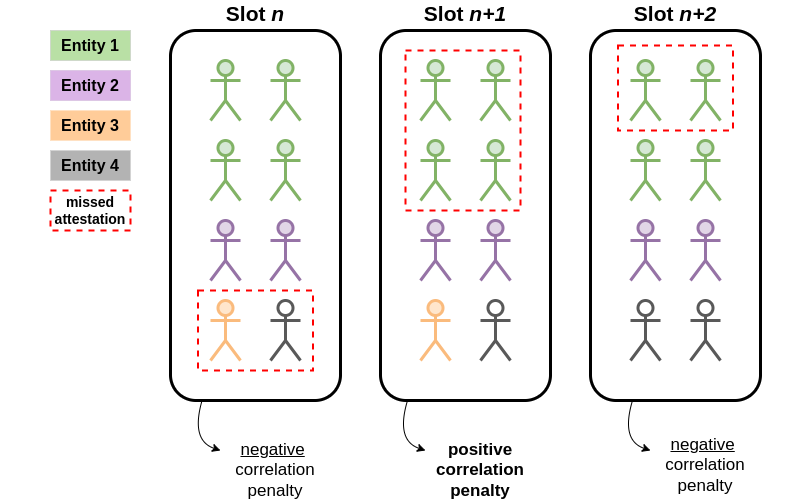
This might look like the following example (assuming a moving avg. of 3 validators):

800×501 25.6 KB

In the illustration above, validators missing their attestations in slots n and n+2 benefit because few others missed theirs at the same time
For slot n+1, a correlation penalty applies due to the number of missed attestations exceeding the moving average threshold of 3 per slot.

Analysis

First, for reproduciability, the dataset I’m using contains all attestations between epoch 263731 (Feb-16-2024) and 272860 (Mar-28-2024).
These are >40 days of attestations, amounting to a total number of ~9,3 billion observations.

In the following, we simulate having implemented the formula that Vitalik suggested (see above) and determine the impact it would have had on attestation penalties. Furthermore, we compare it to the status quo to see what would change.

Staking Operators

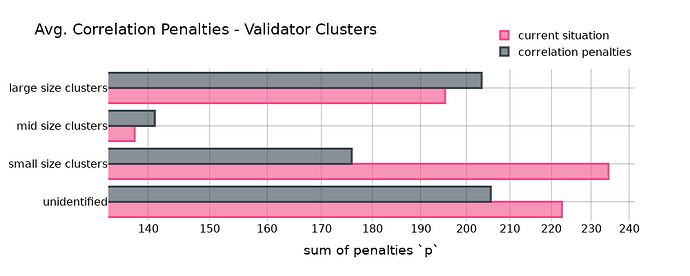
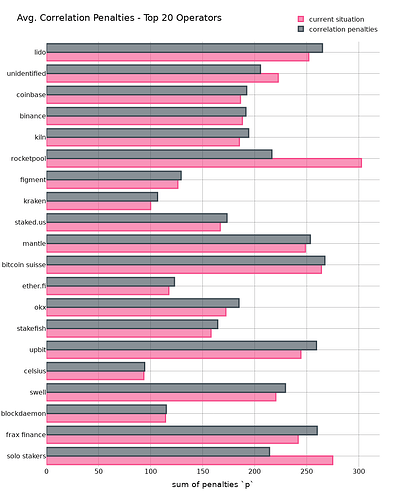
First, let’s look at the sum of all penalties for 4 clusters containing multiple different entities. While the large size cluster contains entities such as Lido, Coinbase or Kiln, the small size cluster is composed of solo stakers and rocket pool stakers. The mid-size cluster is everything in between.

1000×400 18.7 KB

  • The large-size cluster would have had a higher penalty compared to the status quo. The same applied to the mid-size cluster although the effect is less strong.
  • The small-size cluster would have profited by ending up with less penalties.
  • The “unidentified” category comprises around 15% of all validators and definitely contains a large number of solo stakers that weren’t correctly classified as such because my solo-staker-classifier is highly conservative.

This initially confirms the expectation that there exist correlations that cause individual validators to either not miss or miss together with other validators run by the same entity.
→ Check the Appendix I for the same graph showing the individual entities.

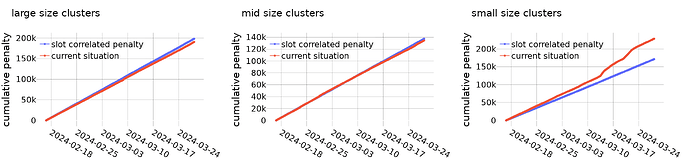
Let’s look at the cumulative impact anti-correlation penalties would have:

2100×500 71.3 KB

  • As expected, for large entities (left), we can see a drift of the “anti-correlation penalty”-line from the status quo. This means that those entities categorized as “large-size” would have had higher penalties.
  • For mid-size clusters (mid), this effect is the opposite, even though it’s not very significant.
  • For small-size clusters (right), we see an improvement compared to the status quo. Those entities would have had smaller penalties with anti-correlation penalties in place.

CL Clients

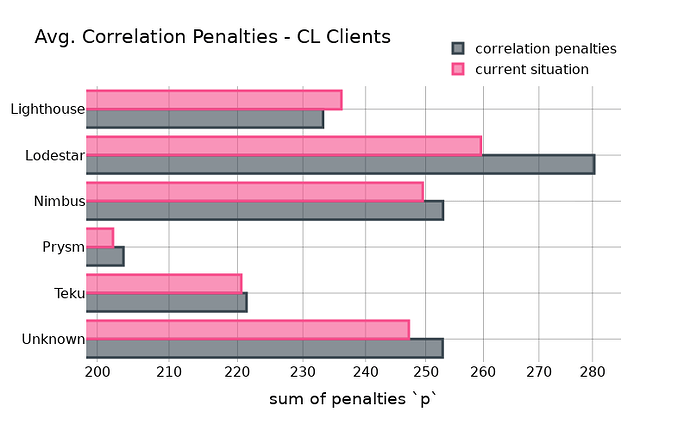
We can basically do the same for CL clients. The expectation is that there is a correlation in validators running the same client. Anti-correlation penalties should thus be higher for validators running majority clients.

800×500 21.4 KB

Small deviations from the “current situation” bar are generally a good sign as it points towards the non-existance of “hidden” client bugs that cause validators missing out to attest - at least for the analysed time frame. Although, we do see some deviations from the status quo for all clients, the effects are rather negligible for Teku and Prysm.
Lighthouse validators would improve their position while Lodestar validators would be worse-off with anti-correlation penalties.

Notable, the result shown in the above chart is heavily depended on staking operators: e.g. if a single large staking operator who is using Lodestar goes offline because of network problems, it directly increases the correlation penalties for the client at the same time, even though the client software might be totally fine.

Conclusion

Implementing anti-correlation penalties is a great way to counter economies of scale without requiring the protocol to differentiate between individual validators.
While this analysis looked and staking operators and CL client, there are many more properties to analyse. This includes, for example, hardware setup, EL client, geographical location, ISP provider, etc.

Finally, anti-correlation penalties are a great way to improve decentralization and the Ethereum community should definitely consider it in future updates.

Appendix

correlation_penalty_entity (10)
correlation_penalty_entity (10)1000×1200 43.2 KB

14 Likes
2

Thank you for running this!

This is a pretty good dataset for this analysis: it has a period of good network stability, and a period of instability on 27th of March. Two other thing that would be super interesting to see in an analysis are:

  1. a period of problems with a client. It’s one network condition where one would expect small operators to fare worse than big ones - they would be just as prone to corellation penalties but higher reaction times and lack of ability to just switch the client would lead to longer exposure to the penalties.
  2. effect of correlation penalties on validators in unpopular geographical locations

Also pretty interesting that these penalties favor Coinbase/Kiln over Lido. That means stakers will have three possible answers to them:
a) DVT
b) diversify validator set a lot
b) concentrate validator set in a small number of excellent providers

5 Likes
3

Could you please make charts start from zero?

1 Like
4

And also not weirdly logarithmic on the x-axis.

1 Like
5

Not sure I agree with conclusion tbh. The practical effect is good for solo stakers, but it’s pretty negligible in amplitude (so not likely to move the needle). Effect can be increased by changing the parameters or having a slightly different mechanism, but at higher penalties one should really be mindful of losing ergodicity. Large pool can afford to play russian roulette with its validators, single validator can’t.

It also makes a middle ground approach (many mid-sized node operators) much worse than strictly centralized setup.

2 Likes
6

Agree with Vasiliy that while this is great for solo stakers and smaller staking protocols, I think the appendix is kinda telling in that increasing such correlation penalties may potentially (even likely) have the opposite of the intended effect of decentralizing the set overall. Decentralized staking protocols with large amount of stake are actually more exposed to correlation penalties than e.g. very streamlined setups like kraken, figment, kiln, celsius etc. In essence, this is telling protocols “you’re doing something wrong, go back to setups with fewer operators who run “tighter” setups”.

It’s pushing NOs (and stakers) to favor more centralized setups but with more “robust” liveliness (e.g. active/active) configurations. Other correlation mitigation penalty methods (DVT, etc) are more complex to implement and execute on (and also costlier), so the inference here would be protocols should basically not bother making such investments and implement all this added technical complexity and just go to like running lots of validators in Point A and an active backup with different clients in Point B. Additionally, it’s very likely punishing toward protocols (like Lido) which have NOs in the set running thousands of validators in less-dense (from a p2p perspective) areas such as Africa and South America, and APAC (where attestation penalties are especially pronounced), and therefore you’ll actively hurt geographic decentralization at-scale.

2 Likes
7

thanks for putting this together! any info on how this maps to actual rewards? I would imagine this being relatively small if you just plot it as the total paid to each validator

8

I’m really worried about item 2 . There are few validators in my country

9

I’m not sure that this would have any significant effect on validators in unpopular geographical locations. If validators are experiencing latency because there aren’t enough validators in their region, they likely wouldn’t have many validators to correlate with for penalty.

This may, in fact, increase geographic decentralization and begin to mitigate problems that validators in unpopular areas experience. Pools that concentrate in specific geographies could be forced to find workarounds to avoid correlation penalties and that would likely include finding ways to validate from new geographies, which would help out the lonely validators in those areas.

I wonder if it could be possible for any historical behavior to be taken into account. The only way I see that a validator in an unpopular location could be adversely impacted is if they happen to miss an attestation in a period when a large pool in e.g. North America is offline and they accidentally fall into that correlation. Supposedly that large pool will already be trying to minimize that effect by decentralizing in all ways possible (including geographically), so this becomes less likely to occur as time goes on but historical correlation behavior being a factor could avoid a coincidental offline event from correlating too heavily with a currently-occurring missed-attestation correlation.

2 Likes
10

Fixed. I had the summed up values before (and used log axis) and forgot to remove the log when switchig to averages.

1 Like
12

The thing with changing incentives is that you change behavior. This analysis is extrapolating what would happen if operators just keep doing what they are doing, but more likely they will work to avoid correlated attestation penalties and missed attestations in general. This could favor larger operations or restrict what kind of setups are viable for smaller operators.

1 Like
13

I share some of the same concerns that this might have the opposite of its intended effect, but I’d like to focus on human behavior during consensus bugs for a minute, while the Nethermind split is still fresh in our collective memory.

During the bug, Nethermind users were faced with an immediate dilemma (whether or not they realized it).

  1. Switch to a different client, risking participating in a finalizing noncanonical chain if Nethermind happens to be correct.
  2. Face downtime penalties on the canonical chain if Nethermind happens to be incorrect.

In this case, the safest option is generally (and was) option 2. By correlating attestation penalties, however, you amplify the losses these risk-averse operators incur, and increase the likelihood that a non-canonical supermajority forms in the event of a consensus split.

Fortunately, geth/besu were canonical, and nobody got slashed for switching from nethermind to a geth fallback, but it isn’t a given.

3 Likes
14

I mean, there’s no need to speculate, one can just check. My intuition is that there is share of network in the region (maybe between 0.5 to 10%?) where correlation penalty already kicks in, but attestation misses because of latency still persist. And I’m pretty sure that the best outcome here the proposal has no effect on incentives for geographical diversity. Most common regions (US, Europe, some parts of Asia) are just better at network quality and will have less penalties in the long run.

2 Likes
15

Good reason for analysis on, not just pools vs ‘unidentified’ validators, but maybe on mid-to-perfect (80-90%?) effectiveness validators to see how they fare in this. I assume it doesn’t meaningfully affect validators that frequently miss attestations (where I assume geographically lonely validators often impacted by high latency sit) because the magnitude of benefit is so large for Rocket Pool in the above charts and Rocket Pool validators aren’t known for their perfect performance.

Also if it’s possible to create some dependence on frequent or continued correlation, that could solve it because these validators are supposedly missing random slots and wouldn’t necessarily look similar to each other over multiple epochs, but that might introduce a lot of complexity (?)

16

Am I the only one who’s surprised that Lido seems to be one of the most affected despite the diversity of their node operator set? It might be interesting to break it down by Lido operator and see if it’s a subset of them or across all of them.

e.g., it seems like their Prysm usage is significantly lower than the rest of the network, maybe that’s being reflected in the data and by implementing strong correlation penalties is it possible that it might create more CL client centralization pressure?

2 Likes
17

I believe many concerns are mitigated by the maximum penalty cap. This ensures that occasional errors do not result in overly harsh penalties and allows validators to quickly recover from such setbacks. Therefore, determining the “right” cap is crucial to avoid the scenario you’ve highlighted, which I completely agree with:

The same applies for unpopular geo locations or client bugs. The current break-even uptime for a validator is 42.5% (see Upgrading Ethereum | 2.8.5 Penalties) which is, imo, very forgiving, but wouldn’t need to be changed (on average).
Furthermore, implementing anti-correlation penalties would not increase the total penalties but would redistribute them from non-correlated parties to those with correlations in their setups.

Regarding Lido vs. other, more centralized entities, I think @tripoli raised a valid point. It would be worthwhile to further analyze how individual Lido operators are impacted by anti-correlation penalties. It’s possible that a few operators, with a significant number of validators, missing their attestation could explain the observed outcomes.
In general, over the long run, we should see Lido outperforming other CEX staking platforms based on the fact that Lido’s node operators are independent from each other, thus reducing correlations.

Also agree that more diversification or DVTs like Obol (h/t @OisinKyne) are a great way for big stakers to reduce the added risk of anti-correlation penalties. If successful, these strategies would effectively achieve their intended purpose.

1 Like
18

I’d disagree with this statement. The key factors for correlated attestation penalties are:

  1. The number of validators a single entity controls.
  2. The fault tolerance of the setup.

Take Lido as an example. It comprises multiple node operators (NOs), where if one NO fails, the others remain entirely unaffected. This resilience is due to different teams, hardware, clients, ISPs, time zones, geographic locations and more. Theoretically, it might be impossible to bring down 100% of all Lido operators simultaneously.

This scenario contrasts with CEXs controlled by a single entity. If a CEX is attacked, it’s much more likely that all of their validators could go offline simultaneously.

Therefore, more fault tolerance equates to more diversification, which results in fewer correlated penalties. Moreover, a robust setup not only mitigates anti-correlation penalties but also encourages big validators to enhance their setup for greater robustness. The ultimate outcome of such improvements is highly beneficial for the network.

I would challenge this view. In the long term, the type of decentralization that involves diverse geographic locations can provide significant advantages. Consider a hypothetical scenario where all US validators fail to attest due to a major outage affecting services like Google and AWS. Although the correlation penalty is capped, those part of the affected group would suffer significantly, while those in other countries would continue to receive their usual rewards. If a similar incident occurred in a less-dense area, the threshold required to trigger an anti-correlation penalty might not be met, potentially resulting in less severe penalties compared to the current situation.

By diversifying validator locations, networks like Lido could better withstand regional outages, thus outcompeting less geographically dispersed competitors.

So, in theory, anti-correlation penalties are even beneficial for pools consisting of multiple independent NOs and would give them a monetary advantage of more centralized setups like CEX.

19

What you describe is actually the goal of anti-correlation penalties: Big operator improving their setups to become more fault-tolerance. This can be achieved in multiple ways, such as moving from cloud providers to home staking, using different ISPs, staking from different countries under different political regimes, or implementing DVTs. So, the change in behaviour would be a great outcome, and if this change leads to a higher fault tolerance, then the goal was achieved.

It’s actually the opposite. In theory, every client with less than a 1/3 validator share (based on the formula that Vitalik initially introduced) would not be affected, while majority clients would face capped penalties. This would provide validators monetary incentives to switch to a minority client, knowing that even if that minority client occasionally performs worse, the resulting penalties over the long run might be lower than those of the well-performing majority client.

20

That is not what I am describing. I point out that we should expect changed behavior and that this should be analysed. We do not know at all what these changes will look like and the changes you list are just some possibilites and in my opinion unlikely, precisely because they do not scale.

I believe it is more likely that big operators are going to optimize (and very likely centralize) their setups, because becoming hyper efficient and reducing missed attestations altogether also reduces impact of correlation penalties and that approach does scale. This would seem like the opposite outcome of what is intended.

So to me the key question here is how operators will react to this proposed change in incentives and unfortunately an analysis that is based on the assumption that there is no changed behavior does not help answering that.

2 Likes
21

I see your point but I don’t think the change in behavior can reduce the effectiveness of anti-correlation penalties. There is only one way to reduce correlation: diversification.

So, either (1) an entity ignores the correlation penalty and focuses on making its current setup even more robust (which is great to see, but costs money), or (2) it diversifies its setup to make sure to reduce correlations (also great but costly).

In scenario (1), those entities might be successful in reducing their overall missed attestation rate, but as soon as there is an issue in their setup it hits them hard.
For example, an entity might be able to reduce the missed attestation rate from 0.001% to 0.0001%, while increasing their cross-validator correlation.
In (2), an entity might remain at the same missed attestation rate but through diversification, that entity can ensure that the penalties aren’t more severe than they are right now (without correlated attestation penalties).

So, what matters is the correlation among an entity’s validators, not the absolute missed attestation rate, assuming there is no chance to reduce the missed-rate to 0.

Citing your comment, which refers to the (1) case I described: Those entities will need to spend money to make their setup more robust, which leads to less profits, which in turn leads to a lower APY that this entity is able to offer to its users. So, great outcome.

1 Like