In the “play to earn” concept, players hope to earn profits while enjoying the game. However, GameFi is constrained by high GAS costs and an underdeveloped blockchain gaming ecosystem, leading to challenges in achieving player acceptance due to issues in security and transparency. This pushes GameFi towards an extreme of constantly optimizing economic models and profit mechanisms, which shortens the earning cycle and may ultimately result in a crash. In the new cycle, the widespread adoption of L2, cross-chain gaming engines, and ZK technology will bring on-chain privacy and more complex on-chain gaming mechanisms to users. This addresses issues of performance, privacy, and trust, shifting focus from Ponzi schemes to more trustworthy and intricate on-chain games. Application-layer ZK technology enables game developers to easily create on-chain strategic games tailored for interactive privacy scenarios, bringing new possibilities to complex and trustworthy (on-chain) gaming scenarios. Salus will discuss in this article how new application-layer ZK technology assists in innovative gaming scenario development.
Technical Background: The Emergence of Recursive zkSNARKs
zk-SNARK is an encryption-proof system where the prover can demonstrate possession of certain information without revealing it, and there is no interaction between the prover and the verifier.
Recursive zk-SNARK implies that developers can verify another zk-SNARK proof within a zk-SNARK proof and generate a statement of the zk-SNARK proof. Recursion allows zk-SNARK provers to compress more knowledge into their proofs while maintaining conciseness, and the recursive verification process does not significantly slow down.
Compared to regular zk-SNARK, recursive zk-SNARK provides enhanced scalability and efficiency by allowing multiple proofs to be compressed into a single proof. This recursive combination reduces the computational load and proof size for complex or multi-step processes, making them particularly beneficial for applications like blockchain games, which involve a high volume of interactions and transactions. This will bring higher performance and lower costs for both users and developers.
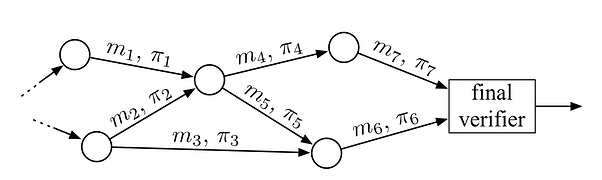
Image source: Signature Merging for Large-Scale Consensus
Recursive SNARKs Unlock New Application-Level Properties
Compression
Recursive zkSNARK allows the prover to put “more knowledge” into a proof while ensuring that these proofs can still be verified by the verifier in constant or poly-logarithmic time. Using recursive ZK SNARK as a “rollup” for information, it is possible to independently “roll up” more computations than what the largest (non-recursive) circuit could handle.
Composability
With recursive SNARKs, it’s feasible to create a chain of proofs where, at each step, a proof is passed to a new participant. Each participant adds their own knowledge statement to it without needing to understand the details of other parts of the chain. This composability aspect allows for the sequential building of proofs, where each participant contributes incrementally while maintaining the integrity and confidentiality of the overall proof structure.
Implementation of Recursive SNARKs.
Typically, there are two methods to implement fully recursive SNARKs:
-
Using Cycles of Pairing-Friendly Elliptic Curves*: This method involves finding two elliptic curves that are pairing-friendly, such that the order of one curve equals the field size of the other. This creates an efficient recursion by utilizing the properties of these curves. However, it’s challenging to find curves that satisfy both pa
Preformatted textiring-friendly and cyclical properties, and this remains an area of ongoing research. -
Forcing Through with Single Pair-Friendly Curve: The second approach is more straightforward, involving the simple implementation of elliptic curve operations for a single pair-friendly curve within the proof system itself. This method does not rely on finding a pair of curves with specific properties but rather works within the constraints of a single curve.
Regarding the first method, the concept of a cycle of pairing-friendly elliptic curves is defined as follows:
Definition 1: A cycle of elliptic curves is a list of elliptic curves defined over finite fields, where the number of points on one curve cyclically equals the size of the field over which the next curve is defined. An m-cycle of elliptic curves is a list of m distinct elliptic curves \frac{E_1}{F_{q1}},…, \frac{E_m}{F_{qm}}, where q_1,...,q_m are prime, such that the numbers of points on these curves satisfy
Efficient zkSNARK constructions are obtained via pairing-friendly elliptic curves, and the cycle condition in equation enables their recursive composition, while avoiding expensive modular arithmetic across fields of different characteristics.
Definition 2: A pairing-friendly m-cycle of elliptic curves is an m-cycle such that every elliptic curve in the cycle is ordinary and has a small embedding degree.
The second approach is to force through and simply implement elliptic curve arithmetic on a single pair of friendly curves in the proof system itself. You could port the pairing circuit to a BN254 curve and then assemble a growth verifier in Circom.
The Groth16 proof system, as an example, features a two-phase trusted setup, where the second phase is circuit-specific. This means that when you validate a proof inside a SNARK, it will require a trusted setup that is independent of the outer SNARK.
Therefore, the most suitable applications for recursive groth16 SNARKs are those that recurse to themselves, meaning the proof verified within the circuit is the proof of the circuit itself. This implies that we only need to perform a trusted setup once. The concept of a self-recursive SNARK is illustrated in the following diagram:
SNARK Self Recursion Image source:0xPARC
At each step, you have a circuit that proves the validity of computation A_i, A_{i+1} …(with perhaps i as a public input to the SNARK), and within the i th such proof, you verify another proof showing validity of computation A_{i+1}, A_{i+2} … alongside step Ai’s validity. At each recursion, your SNARK circuit would remain the same. In the case of Isokratia, for example, each of the Ai s are ECDSA signature verifications.
In summary, recursive zkSNARKs offer enhanced scalability: they reduce the data and computation required for multi-step games or actions, making them more feasible on-chain and ensuring that complex game logic and state transitions are verified quickly and securely.
Case Study: ZK-Hunt and Its Impact
ZK-Hunt is an RTS-style PvP game on the blockchain that explores the use of ZK technology to implement complex on-chain game mechanisms and information asymmetry. ZK-Hunt allows players to execute actions in complete privacy, enabling the verification of each action without revealing any underlying data.
Movement through the plains is public, illustrated by the fact that player B can see player A’s position update as they move. Entry into the jungle is also public, but moving through the jungle is private, such that player A loses track of player B’s position in the jungle, and can only simulate a growing set of potential positions, which are shown with the question marks. Exiting the jungle back into the plains is again public, and so the set of potential positions collapses.
This information-hiding behavior is fundamental to ZK Hunt; units have a state (their location) that can switch from public to private and then back again based on actions in the game. This enhances the strategic depth of the gameplay.
The state verification process in ZK Hunt primarily involves the following steps:
- Locally update the private state: transition from S_{i-1} to S_i (switching from public to private or vice versa).
- Generate proof of a valid state transition: utilizing S_{i-1} and S_i (along with the previous commitment C_{i-1} , to generate a new commitment C_i ).
- Submit the proof for on-chain verification (the contract provides a value for the commitment C_{i-1} to ensure the proof is correctly generated).
- Update the commitment on-chain (store C_i so it can be used as C_{i-1} in the verification of the next transition).
A commitment is a tool that ZK proofs can use to validate some private state previously “committed to” by the user, without revealing that state to the verifier. The user provides the commitment C as a public input to the proof and the private state s as a private input. The proof internally computes the commitment that s would produce and checks if it matches C :
template Example() {
signal input state; // Private
signal input commitment; // Public
// Calculates the poseidon hash commitment from 'state'
signal result <== Poseidon(1)([state]);
result === commitment;
// The rest of the circuit can now trust the validity of 'state'
...
}
component main {public [commitment]} = Example();
Although the cost of verifying ZK proofs is considered constant (at least for certain proof systems like Groth16), in reality, this verification cost increases with the number of public inputs, which can be significant during on-chain verification. Meanwhile, ZK Hunt employs the Poseidon hash as its commitment scheme because it is much more efficient to compute within circuits compared to other common hash functions, requiring fewer constraints per message bit. If the private state is a value randomly chosen from a sufficiently large range (such as a private key or random seed), then simply obtaining the hash of this value is enough to serve as a commitment.
There are many other game innovation scenarios that can be realized by similar ZK technologies, such as asset hiding, decision privacy, and progress confidentiality.
Asset hiding: In set-and-forget card games, players can use zero-knowledge proofs to hide their hands and only show necessary information when playing cards.
Decision Privacy: In strategy games, players can secretly choose their next move or allocate resources, and these choices are only made public at specific points or when triggered by game logic.
Progress Confidentiality: In adventure or role-playing games, players may complete quests or earn achievements without others knowing exactly what they have accomplished, thus maintaining an element of surprise or competitive secrecy.
By employing zero-knowledge proof technology, ZK Hunt allows players to play while maintaining privacy. This is not only a technological innovation, but also a rule change in on-chain gaming. In this way, game actions are verified without revealing sensitive data, enhancing the covert nature of the strategy and enriching the strategic depth and surprise element of the game.
If you are interested in integrating ZK technology in on-chain games to enhance privacy,scalability and enable game innovation, Salus offers end-to-end ZK services and comprehensive solutions. By collaborating with us, you can explore a wide range of applications for ZK technology in the gaming space, providing players with a richer, safer, and more strategic gaming experience.