Confirmation Rule for Ethereum PoS

Consensus
1

This post is opened for discussion re. the following fast confirmation rule for Ethereum proof-of-stake:

This work was conducted together with Francesco D’Amato @fradamt, Roberto Saltini @saltiniroberto, Luca Zanolini @luca_zanolini, & Chenyi Zhang.

Confirmation Rule

Assumptions:

  • From the current slot onwards, the votes cast by honest validators in a slot are received by all validators by the end of that slot, i.e., the network is synchronous with latency < 8 seconds.
  • This proposed change to the Ethereum protocol:
    • If j is the highest justified checkpoint block, and the current epoch is e, then allow a branch with leaf block b if the latest justified checkpoint in the post-state of b is either j, or from an epoch \ge e-2

Notation:

  • n is the current slot, and e is the current epoch.
  • b is a block from the current epoch e.
  • There are S FFG votes from epoch e in support of c.
  • W_f is the weight of validators yet to vote in epoch e, and W_t is the total weight of all validators.
  • The adversary controls \beta < \frac{1}{3}^{\textrm{rd}} fraction of the validator set.
  • The adversary is willing to bear a slashing of \alpha (\leq \beta) fraction of the validator set.

A short description of the rule (please see confirmation-rule-draft.pdf (396.2 KB) or blog post for explanation):

  • p_{b}^n = \frac{\textrm{honest support for block } b}{\textrm{total honest weight}} from validators in committees from b\textrm{.parent.slot} + 1 till n.
  • \textrm{isLMDConfirmed}(b, n) is defined as p_{b'}^n > \frac{1}{2(1-\beta)} for all b' in the chain of b.
  • \textrm{isConfirmed}(b,n) if:
    • the latest justified checkpoint in the post-state of b is from epoch e-1, and
    • \textrm{isLMDConfirmed}(b,n), and
    • [S - \textrm{min}(S, \alpha W_t, \beta (W_t - W_f))] + (1-\beta)W_f \ge \frac{2}{3}W_t.

If \textrm{isConfirmed}(b,n), then b is said to be confirmed and will remain in the canonical chain.

Since p_b^n cannot be observed, we define a practical safety indicator q_b^n to determine if p_b^n is in the appropriate range:

  • q_{b}^n = \frac{\textrm{support for block } b}{\textrm{total weight}} from committees in slot b\textrm{.parent.slot} + 1 till slot n
  • q_{b'}^n > \frac{1}{2} \left(1+\frac{\textrm{proposer boost weight}}{\textrm{total honest weight}}\right) + \beta for all b' in the chain of b implies \textrm{isLMDConfirmed}(b, n)

Performance

In ideal conditions, the rule would confirm a block immediately after the end of its slot.
Under typical mainnet conditions, we expect the rule to confirm most blocks within 3-4 slots (under 1 minute).

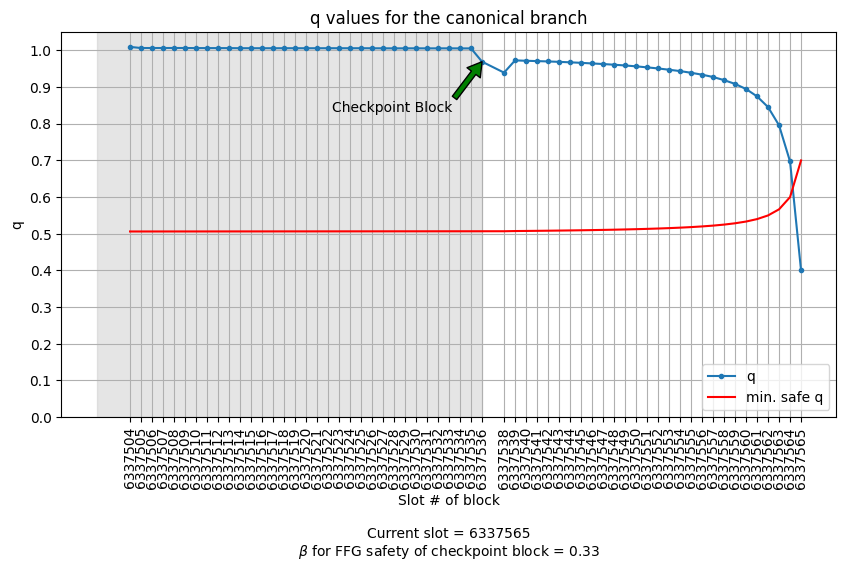
We observe the following values for q (plot generated using this prototype):

q_plot
q_plot846×571 38.5 KB

The current slot is 6337565, and the latest confirmed block is at slot 6337564.

Previous Work

2 Likes
2

Please change to “total weight from slot(b’.parent)+1 to n”

1 Like
3

I have found a very easy way to delay the confirmation time forever.

First, I describe the way to delay the confirmation time from one slot to one epoch.

In the function isLMDconfirmed specified in spec, confirming a block requires that its last 32 ancestors are also LMD confirmed.

However, the adversary can delay the release of a block to prevent its confirmation. In particularly, if a block is released at the 2/3 of the slot, almost no attestations support it. This leads the block can not be confirmed. Therefore, the next 32 blocks with the delayed block as the ancestor cannot be confirmed.

As a result, the strategy to delay the comfirmation time forever is delay a block during every epoch.

4

If almost no attestations support the block, can the block not be trivially re-orged by the next proposer using the late block re-org feature?

5

The answer is yes, I think. However, the block proposer can release the block between 4s to 4.5s after the slot starts, to make it not be re-org and also not be confirmed.

6

If you release a block at second 4s to 4.5s the likelihood of this block getting reorged is very very high. Without doing any analysis on it, I’d say about as high as the market share of prysm and lighthouse as both support honest reorgs.

7

I think the release time is not an vital issue.

I believe that if the block proposer releases its block just before validators release their attestations (e.g., at 3.9 seconds), there is a likelihood of a condition where at least 20% and at most 50% of validators receive the block before attesting. I believe this release time can be measured.

Even the precise determination of the release time may be challenging, an adversary holding a 20% stake could attest to its delayed block to prevent it from being reorganized by honest validators.

Therefore, I find it highly probable that such a scenario may occur.

8

This is only causes a minor slow down of the confirmation rule. If the block stays in the canonical chain, it will keep accruing weight and eventually be confirmed, regardless of what the weight it accrued in its own slot is: as more slots and more votes accumulate, that original weight becomes less and less important. If instead it doesn’t stay in the canonical chain (i.e. it is reorged), then it becomes irrelevant to the confirmation rule.

1 Like
9

We have just released here a paper presenting an updated version of the confirmation rule algorithm described in this post.

1 Like