TL;DR
A payment system inherits security from Ethereum’s Layer 1. Senders can send money from any Rollup that can import and read the state root of other networks. Receivers can withdraw on a specified Layer 2 or Ethereum Layer 1. Payment channels are used, and neither the sender nor the receiver will lose money even if they are offline for an extended period. An intermediate hub must be online to avoid asset loss.
Background
The DA Attack problem is a specific issue with scaling smart contracts that have rich statefulness, and the Ethereum community lacked sufficient discussions on scaling payments beyond Plasma. Additionally, Rollups were fragmented, requiring a configuration of a payment system that does not create a double-match problem between payers and recipients concerning network selection.
Approach
Using a Merkle Tree for Airdrops is an efficient method suited for making simultaneous payments from a single user to multiple recipients. To facilitate recipients in consolidating multiple incoming payments, each user calculates a Zero-Knowledge Proof (ZKP) on the client side. However, it’s uncommon for a typical user to engage in mass payments from a single user to multiple users. This type of transfer is confined to hub nodes, and the focus is on how to enable many senders to collectively share this mass payment. Here, we introduce ZKP-based Hashed Time-Locked Contracts (HTLC). Instead of requiring the submission of a preimage, the completion condition for the HTLC is a ZKP proving the successful execution of the aforementioned mass payment. Using this approach with payment channels, transactions from numerous senders to multiple recipients can share a single Merkle Tree Root of 32 bytes. By configuring the payment channel as one-way, the online requirement for the sender can also be eliminated.
Construction and Procedure
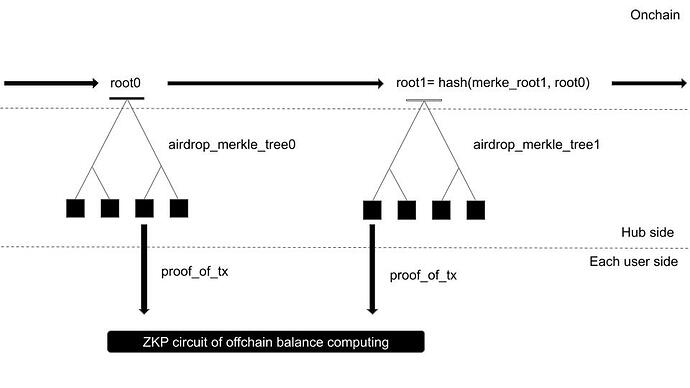
First, designate the intermediate hub as the sole node, naming it Bob. Bob deposits a fixed amount into the smart contract 0xS on a Rollup or Ethereum Layer 1.
For example, 1024 senders, Alice0 to Alice1023, each create a payment channel with Bob on their preferred Rollup. This payment channel is unidirectional, with Alice’s balance decreasing continuously while Bob’s balance increases. In essence, it is a one-way payment channel dedicated to Alice’s payments.
There are 1024 receivers, Carol0 to Carol1023, each with an address available on their respective Rollup to identify them.
Alice constructs a payment transaction to Carol as follows: (Carol’s address, amount, nonce)
Alice creates an off-chain commitment for the Payment Channel, moving the balance equivalent to the specified amount to Bob. Bob also signs this commitment. At this point, the HTLC condition states that Bob must prove, through Zero-Knowledge Proofs (ZKP), that the same amount has been paid in an upcoming airdrop from him to Carol. In other words, payment is completed for Alice if she receives the ZKP for the airdrop after this commitment.
Bob executes the payment via airdrop using the following steps:
-
Bob aggregates the hashes of transactions received from Alice0 to Alice1023 into a Merkle Tree.
-
Bob provides the proof of each transaction (proof0 to proof1023) to Carol0 to Carol1023 respectively, and they sign the Merkle Tree’s Root.
-
Bob creates ZKP data (zkd) to prove that the sum of signed transactions within the Merkle Tree exceeds his deposit balance.
-
Bob writes the aggregated signature data (like BLS) and the Merkle Tree’s Root to Layer1 storage. He also hands over proof0 ~ proof1023 and zkd to Alice0 ~ Alice1023.
Special Note: the tree roots should be unified with the lastest one so that all the payments can get proved to be included in the latest one root. Then the each root needs to include the previous root or a root of a Merkle Tree of all roots submitted before.
Carol withdraws from the smart contract 0xS using the following steps:
- A Sparse Merkle Tree generated from the hashes of Carol’s already withdrawn transactions is stored in the storage.
- Carol, for all the transactions she wants to withdraw, includes in the Zero-Knowledge Proof (ZKP) circuit:
- SMT non-inclusion proof
- zkd
- Proof of inclusion in the transaction Merkle tree
- Aggregated signatures This allows her to prove the total withdrawal amount. Given the ability to provide withdrawal proofs for an unlimited number of transactions, a circuit with cyclic recursive ZKP is desirable.
At this point, the SMT is updated.
Alice/Bob perform withdrawals from the network as follows:
-
If both parties are in agreement, withdrawals can be executed with a second signature from both parties concerning the latest commitment. It’s essential to note that this signature for withdrawal occurs separately from the one made during the HTLC commitment.
-
If both parties do not agree, initiate a withdrawal request with the latest commitment and wait for the challenge period (e.g., 7 days).
Response to Attack Vectors and Edge Cases
- If Bob fails to provide proof/zkd to Carol or if Carol doesn’t sign upon receipt.
In either case, the transaction is canceled. This is because BLS signatures are included in the withdrawal ZKP circuit.
- If Bob fails to provide Proof or zkd to Alice.
If Alice does not receive Proof or zkd from Bob promptly, she takes immediate action to close the channel. If Bob has made the payment, Proof and zkd are submitted during the on-chain challenge and finalized with the latest commitment. If Bob has not paid, it is confirmed with the previous commitment. It’s important to note that if data is not provided, Alice will not proceed with the next payment.
- If Alice/Bob attempt to withdraw with an old commitment.
In a one-way payment channel, Alice’s balance only decreases, and Bob’s balance only increases. When Bob attempts to withdraw with an old commitment, he will always incur a loss, so Alice does not need to be online. If Alice attempts to withdraw with an old commitment, Bob must challenge it to invalidate it, but since Bob is always online, this is not a problem.
- If a Rollup remains down for a waiting period of 7 days or more:
If the waiting period is defined using block height, there should be no issue.
However, if only Unix time is being used, users may be unable to execute challenge or close smart contracts, potentially compromising the security of the Payment channel. To avoid this, appropriate measures should be taken.
Practical Improvements
- Elimination of Aggregated Signatures
Reducing the size of the circuit is possible by eliminating the receipt signatures from Carol. In this case, an attack where Bob does not provide proof/zkd to Carol is possible, but Bob has already made the payment, so he doesn’t gain or lose anything. Carol simply needs to provide the service of holding the payment until she receives the data from Bob or Alice.
- Shorter Confirmation Intervals
Long confirmation intervals, meaning long intervals between the submission of Roots, result in waiting for payment completion during that time. In practice, it is preferable to generate Trees at 20-second intervals using a Capped Merkle Tree or similar, and then concatenate them on-chain to create the final Root. This may slightly increase calldata usage but keeps storage usage the same.
- Instant Finality
Similar to other zkRollups, Trusted finality with penalties can be achieved through block producers (in this case, tree producers) providing insurance. It’s preferable for the insurance pool to be separate from the deposit pool.
- Relationship and Application with Intmax2
Intmax2 [2] is a Layer 2 payment system that optimizes and parallelizes client-side validation (off-chain balance computing) using recursive zkp which provides incrementally verifiable computation or succinctly verifiable proofs. Originally, this post emerged as an approach to address the technical challenge of sharing the capability, inherent to Intmax1/2, of including a large number of token transfers within a single transaction with approximately 5 bytes of calldata. The method of fund transfer via airdrop using BLS signatures and Merkle Trees is essentially a simplified version of Erik Rybakken’s Intmax2, made unidirectional with only the hub (Bob) as the sender. Applying this approach to Intmax2, specifically incorporating this special HTLC into Intmax2’s ZKP circuit, would also enable bidirectional fund transfers. In this case, the one-way payment channels still remain, and incoming transactions are always airdrops.
Relationship with Stateless Limits
The paper “Limits on revocable proof systems, with implications for stateless blockchains,”[3] published in 2022, formally demonstrates that linear growth in state size with respect to the number of users is basically inevitable for all types of blockchains. It can be seen as a more general formulation of the DA problem that the Ethereum community discovered during the research on Plasma in 2018. This approach does not break the limit of linear growth with respect to the number of users but achieved to minimize the slope of that linear growth to an ignorable number. The state growth per user is 32 bytes (the size of the channel), and 0.0032 bytes per transaction if each airdrop tree has 10K txs.
Privacy
The hub (Bob) knows the content of transactions. On-chain, the transactions are not analyzable, and neither the sender nor the recipient is visible.
Conclusion
Regarding payments, this approach has achieved nearly complete liberation from the cost issues associated with DA, on-chain privacy, and a certain degree of interoperability between Rollups, all without imposing a burden on users. For users, it can be said that the scalability expected from Plasma[4][5] has been achieved alongside the same “no online requirement” as Rollups. Bidirectional fund transfers require integration of the ZKP-based HTLC with Intmax2.
Reference
[1] Dompeldorius, A. “Springrollup”
[2] Erik Rybakken, Leona Hioki, Mario Yaksetig “Intmax2”