Leona Hioki, Albus Dompeldorius, Yutaka Hashimoto
Abstract
We introduce a new kind of blockchain scaling solution, which can be classified as a kind of Plasma, but without the online requirement of users. Our design satisfies the following requirements:
-
- O(1) state growth per block relative to the number of users before withdrawals
-
- No need for channels or individual liquidity preparations between recipients and the hub
-
- Elimination of online requirements for general users except during sending and receiving (No need of watch tower)
-
- Onchain privacy
This is the practical pseudo-solution of the the impossibility of stateless blockchains proposed in 2022. We can delay the problem proposed in the paper as long as we want.
Code & Mainnet Demo: github plasna-next
Background
The scaling solution for programmable blockchains such as Ethereum to accommodate an increasing number of users, Plasma, was frequently discussed in 2018. It is a Layer 2 with O(1) state growth per block, which, in the recent context of Financial Cryptography, is classified as a stateless Layer 2. Subsequently, to avoid the heavy online requirements, i.e., updating proofs or witnesses, and to prevent Data Availability Attacks against smart contracts, development moved towards Rollups, which utilize Layer 1’s cheaper storage space for data availability. A method that could eliminate online requirements while providing the same level of O(1) scaling as Plasma was the goal needed to achieve for the practicality reason.
Prerequisites
Bulk-Token-Transfer
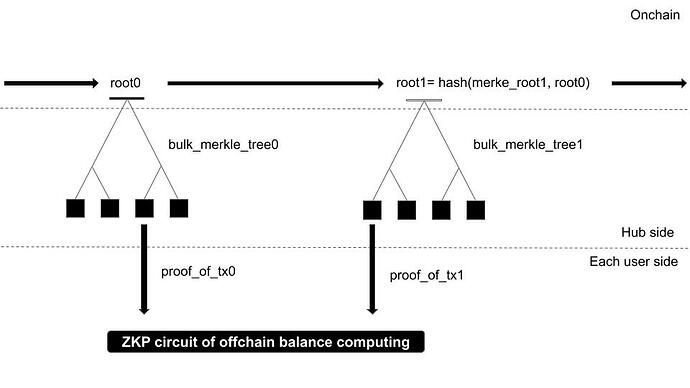
The sender inserts the recipient’s address and the amount to be sent into each leaf of a Merkle Tree and generates a Merkle Root. Then, the sender creates a ZKP with the total amount sent and the Root as public inputs and allocates the funds accordingly. Each recipient is given their corresponding leaf and Merkle Proof, along with the ZKP, to complete the transaction. Even if a recipient receives multiple such transactions, they can efficiently prove the aggregate of these ZKPs and Merkle Proofs on their client-side, for example, through recursive ZKPs. Only the root gets recorded on Layer1, it makes the O(1) state growth unless there is no withdrawal verification on Layer1.
ZKP-TLC
HTLC (Hash Time Locked Contracts) is a technology for conditional payments used in multi-hop payment channels, such as the Lightning Network. In the case of an HTLC where a user, Alice, makes a payment to an operator/hub, Bob, Alice sets the hash value hash(preimage) of a randomly specified value preimage in that HTLC. If Alice can somehow learn and submit the preimage, say, by being told by Bob, then the payment is completed. Otherwise, the payment is canceled after a certain period. It is also possible to create a modified version of HTLC where the part about revealing the preimage is changed. For example, an HTLC from Alice to Bob could be conditioned on Bob having made a payment to Carol if there is a ZKP of it, as used in this paper. Let’s call an HTLC modified to set the verification of a ZKP as its condition a ZKP-TLC.
One-Way Payment Channel
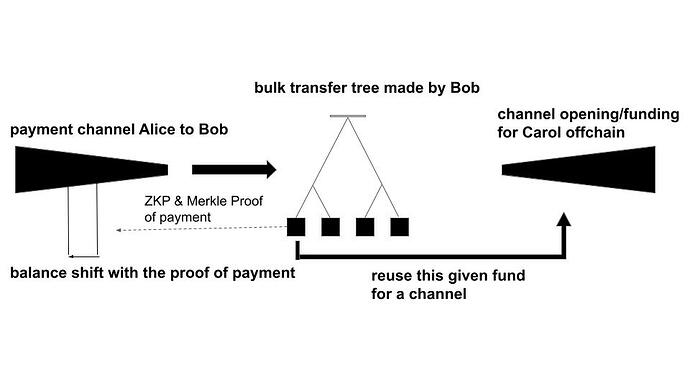
In a bidirectional payment channel, since both balances can increase or decrease, an attacker retroactively cancels a transaction by closing the channel with an outdated balance unless it’s not watched over, thus requiring both parties to constantly monitor the Layer 1 chain for channel closure. However, in a one-way channel where only one party’s balance decreases, any channel close other than the most recent commit always benefits the sender, Alice. In this case, the sender, Alice, no longer needs to monitor Layer 1, freeing her from the online requirement. In the overall structure of this paper, the balance update condition for the payment channel from Alice to Bob is set to a ZKP-TLC, which is fulfilled by sending a proof of a bulk-token-transfer from Bob to Carol.
Off-chain Channel Opening/Funding
In conventional payment channels, channel opening/funding is performed on-chain, whereas this can be replaced by receiving a bulk-token-transfer with a Merkle Tree. On the blockchain, the block number of the last bulk-token-transfer withdrawal made by each user is recorded. When a user or Bob withdraws, they must prove the entire amount received, i.e., the channel capacity, using ZKP. This prevents the possibility of withdrawing the same receipt twice. Furthermore, preventing Bob from proving a lesser amount is safeguarded by Alice signatures during channel updates. The channel is updated while agreeing on the channel capacity. This part also makes Plasma Next bidirectional.
Method
TL;DR: There are 2 ways to do stateless payments which do not make onchain data cost, bulk-token-transfer and payment channel. Bulk-token-transfer, which is a transfer from a single sender to multiple recipients, uses only a fixed onchain cost of 32 bytes. It is possible to share this fixed cost among many senders by using payment channels in a trustless manner. If we use one-way payment channel, we can eliminate the online requirement. The receipt of a bulk-token-transfer can be directly converted into off-chain channel opening/funding, enabling bidirectional transfers and keeping the system stateless.
The hub of a single payment channel is referred to as the operator. Since the system has and needs only one payment channel hub, this paper does not consider hops beyond one since it’s not required. The paper proposes using ZKPs and Merkle Proofs of payment for closing payment channels, eliminating the need for long-term online requirements. Instead of submitting a hash’s preimage as the condition for an HTLC in a payment channel, it uses the proof of asset distribution in a Merkle tree and a ZKP of the total amount distributed across the tree. Hereafter, the sender is Alice, the hub operator is Bob, and the receiver is Carol. In this system, a Payment Channel is open between Alice and Bob, and initially, there does not need to be a channel between Bob and Carol. Users do not open channels with anyone other than Bob.
Bob employs a bulk-token-transfer with a Merkle Tree for making payments to numerous recipients. All payments to the recipients are recorded in the leaves of a Merkle tree, and Bob also creates a ZKP of the total amount for these payments. The funds used for payments in this Merkle tree are managed completely separately from those in the channel. Instead of using a conventional ZKP-TLC for the update condition of the oneway payment channel from Alice to Bob, a ZKP-TLC that is satisfied by submitting a Merkle Proof and a ZKP of a corresponding bulk-token-transfer.
-
- Bob receives information from Alice about the payment amount from Alice to Carol.
-
- Alice sets the condition of the ZKP-TLC such that the balance of the channel between Alice and Bob changes only if a bulk-token-transfer of an equivalent amount from Bob to Carol is successful. Both Alice and Bob sign this ZKP-TLC. The data of the ZKP-TLC also includes the total amount Alice has received since the last withdrawal, which represents the capacity of this payment channel, and this is simultaneously signed as well.
-
- Bob creates a Merkle tree aggregating such payments in bulk (there are many Alice and Carol pairs in this world), meaning that he put the merkle root onchain.
-
- Bob provides Carol (and Alice) with the path and data for Carol’s payment within the Merkle tree. For Carol, this also functions as channel opening/funding.
The payment is not completed until Carol receives the data, giving Alice, the sender, an incentive to provide the data to Carol herself if Bob fails to do so. Carol is not obligated to provide any service in back if she does not receive the data.
The contract for on-chain withdrawal (channel close) contains the following data:
For common,
allTreeRoot: The root of a Merkle Tree made by all roots of bulk transfer trees
For each user,
lastBlockNumber: The block number of the last withdrawal by Alice
Closing the channel can proceed as follows:
-
- Prove and submit the total amount received from the proofs using recursive ZKP. The total amount should be greater than or equal to what was signed from both sides when the channel was updated.
-
- Submit last balance of Bob within the channel, which is signed by both.
-
3.The difference in balance is the amount that can be withdrawn.
In this scenario, if Bob makes channel payments without verifying the ZKP, Bob is at a loss. Withdrawals exceeding the total channel amount are not possible, preventing any deception across the protocol or the pool.
Therefore, deposits into the channel are enabled by proving the total amount received from the proofs using recursive ZKP. Essentially, all money received via the bulk-token-transfer can be considered for deposit into the channel.
Regarding Channel Closing:
Channel closure can occur when Bob wishes to close the channel or when Alice or Carol wants to close the channel and Bob agrees, under the conditions that:
-
- Both signatures are present on the ZKP-TLC,
-
- The conditions of the ZKP-TLC have been satisfied.
There is no challenge period for these scenarios.
If Alice or Carol wishes to close the channel but Bob does not agree, closure can still proceed if:
-
- Both signatures are present on the ZKP-TLC,
-
- The conditions of the ZKP-TLC have been satisfied,
-
- There are no other ZKP-TLC submissions from Bob during a challenge period.
Malicious Patterns and Responses
There is no need of “exit game”, but we need patternized procedures for some edge cases.
1. If Alice attempts to close with an outdated commit
Bob, who is always online, can activate the latest commit onchain by submitting it, just as in a normal payment channel. This submission includes the Merkle proof for the bulk-token-transfer and the ZKP of the funds as inputs to the ZKP-TLC condition onchain.
2. If Bob attempts to close with an outdated commit
Since Alice’s balance only decreases and an outdated commit would be in Alice’s favor, it can be ignored.
3. If Alice attempts to withdraw a bulk-token-transfer more than once
Withdrawn bulk-token-transfers have a corresponding Layer1’s lastBlockNumber, and within the ZKP circuit, it is verified that there are no duplicate transactions, preventing the possibility of double withdrawals.
4. If Alice tries to use a received bulk-token-transfer as funding in the channel with Bob more than once
As mentioned above, since the onchain cannot be deceived, Alice and Bob are in a zero-sum game regarding this point. Bob only needs to verify Alice’s funding source in the same way the onchain verification mechanism would.
5. If Bob does not proceed with the bulk-token-transfer after setting the ZKP-TLC
In a friendly scenario, both parties can agree to cancel the payment with their signatures. Otherwise, both Alice and Carol may choose to close the channel.
6. If Bob does not provide Alice with the bulk-token-transfer’s ZKP and Merkle Proof
Alice closes the channel. Bob then submits the proof onchain, making it possible for Carol to become aware of it as well. Since Bob has already allocated the funds to Carol, Alice could choose to ignore this situation. However, if Carol has not received the data, the payment to Carol remains incomplete, giving Alice an incentive to ensure that the data is transferred to Carol.
7. If Bob, after updating Alice’s lastBlockNumber through closing, reveals the existence of previously hidden bulk-token-transfers to Alice that occurred before the lastBlockNumber
It is essentially important to prevent this withholding attack by the sender to Alice, yet there could be cases where the sender attempts to do so while closing. Assuming Alice will notice these transfers after a relatively short period, it is desirable that if the amount received upon closing is less, Alice should be able to recalculate it. Since Alice should have kept all the receiving proofs at least after the last withdrawal, she should be able to calculate the recalculated amount and receive the difference from what was received at Bob’s closing.
Therefore, add the following to the storage for each user (not added to all sections for clarity of explanation):
previousBlockNumber: The block number of Alice’s penultimate withdrawal.
lastWithdrawAmount: The last withdrawal amount, i.e., the amount withdrawn between the previousBlockNumber and the lastBlockNumber.
8. When Bob attempts to finalize Alice’s withdrawal amount during channel closing with a smaller channel capacity
Since Alice has not signed off on this channel capacity, the onchain verification will not pass.
Avoiding the impossibility of Statelessness
A paper published in 2022 addressed the limitations of stateless blockchains with O(1) state growth. This was a groundbreaking formalization and theorization of limitation felt by the Plasma community facing Data Availability problem in 2018, turning many researchers skeptical towards stateless blockchains. The pseudo-solution proposed here achieves statelessness in the absence of channel closures for withdrawals or dispute resolutions. In short, we can delay the problem proposed in the paper as long as we want since the channel opening and the transfer process are in a stateless manner, and only the withdrawal requires state data onchain.
The paper posits that a stateless cryptocurrency is not feasible because it necessitates choosing between linear state growth with the number of users or an increase in local proof updates. However, this limitation is based on the premise that an increase in local proof updates is unacceptable. In the context of payment channels, this premise falls apart as Alice only needs to notify Carol about the given proof updates, motivated by a strong incentive to do so. This significantly differs from scenarios where shared assets in smart contracts have no protection against the threat of proof updates, i.e., Data Availability Attacks. Without rich stateful smart contracts, local proof updates are not a threat, and online proof distribution is feasible. Payment channels do generate state growth in the event of disputes, but if there is no dispute and the channel does not close, the opening of channels is possible through the distribution of merkle proofs, and payment transactions do not generate state growth, thus maintaining statelessness.
To succinctly capture the achievement of this stateless system within the context of the limitations of statelessness, focusing on payments and concentrated online requirements to specific nodes has enabled O(1) state growth without harmful proof updates.
Programmability: Stateless Applications and Stateful Applications
Developers can build applications with EVM. Verification on the ZKP-TLC side is conducted on an EVM smart contract written in Solidity or similar languages. Ultimately, whether it is valid on-chain becomes the criterion for off-chain verification, allowing for the execution of EVM bytecode to be added. In a relationship confined between Alice and Bob (Operator), it is possible to set all on-chain verifiable transactions made by Bob as conditions for the ZKP-TLC from Alice to Bob. It is considered possible to extend this to include Carol using bulk-token-transfers.
The methods described above make it possible to construct applications that are inherently stateless. Applications that possess rich statefulness, such as having a contract address managed by the entire protocol, are challenging to support with Plasma alone. However, by utilizing smart contracts from other rollups, it is possible to create stateful applications. In this case, the advantage of Plasma Next lies in the separation of scalability for smart contract execution and scalability for transfers. Transfers can be conducted in a stateless manner at extremely low costs, while the execution of rich-stateful smart contracts can be performed with the usual scalability of rollups.
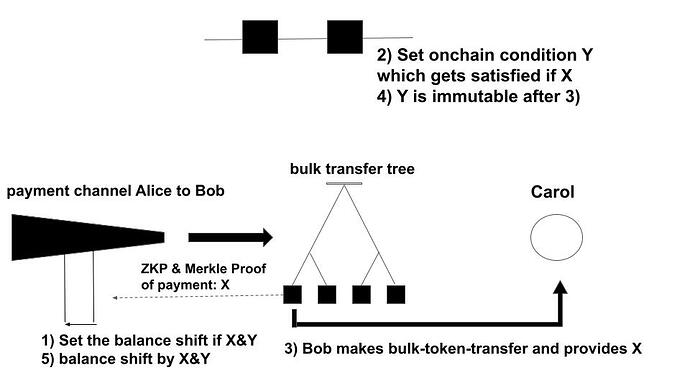
A specific implementation method involves a smart contract that verifies ZKP-TLCs in a payment channel and only requires reading the storage of other smart contracts. This allows the conditions of the ZKP-TLC to be set based on the storage state of other smart contracts. An important point is that this storage has an immutable nature, meaning it is necessary to be able to withdraw under the same conditions even after some time has passed and the channel is closed.
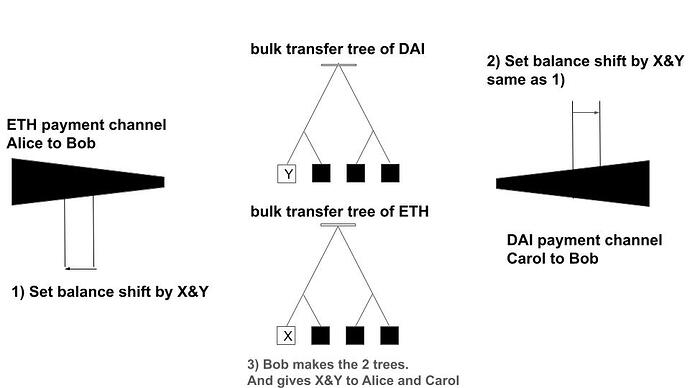
We can construct the protocol like this. The condition of the ZKP-TLC from Alice to Bob is defined as the proof of a bulk-token-transfer, labeled X, and an onchain storage, marked Y. The contract is configured such that the onchain storage Y is immutably finalized only when X has been satisfied. Only after these prerequisites are confirmed can Bob proceed with the bulk-token-transfer. Once Y is settled, the ZKP-TLC is also considered settled. Programming Y as a transfer of value from any Carol to Alice would enable the construction of an extensive DEX.
Meanwhile, executing this transfer of value from Carol to Alice as a transaction on Plasma Next becomes feasible by setting the proofs of both transfer trees as the conditions for the ZKP-TLCs of both parties.
If Bob does not make both trees, the swap will be canceled. If Bob makes only one of them, Bob will lose his fund of the payment.
In short, if the completion function of ZKP-TLC is a pure function in the context of EVM, it is a stateless application. If a view function is necessary, then it is a stateful application.
Challenges
The operator conducts transfers using a separate Merkle tree from the channel, requiring liquidity separate from that of the channel. This implies a deterioration in capital efficiency. Fortunately, the hub can close the channel immediately since the last commitment is always the best for a hub in a one-way payment channel. So a well-managed closing operation is basically the best solution of this problem.
Conclusion
In the specific context of payments, it has been possible to eliminate the online requirement from Plasma. This result, in other words, suggests that the Turing completeness of Ethereum and ZKPs can eliminate the need for online requirements to monitor the network—such as the need for watchtowers—and even the necessity to open channels for receiving payments.
Related Works
- Plasma by Joseph Poon and Vitalik Buterin
- Plasma Cash by Vitalik Buterin
- Plasma Prime
- Plasma Snapp by josojo
- Cross Rollup Payment Channel
- Lightning Network by Joseph Poon and Thaddeus Dryja
- bitcoinj. Working with micropayment channels
- Impossibility of Stateless Blockchains
- Limits on Stateless Blockchains by Miranda Christ and Joseph Bonneau