Deterministic Consensus using Overpass Channels [𝗏.2] in Distributed Ledger Technology

Layer 2 State channels
1

Brandon “Cryptskii” Ramsay
[email protected]
November 26th 2024

Abstract

This paper presents a formal analysis of the Overpass protocol, a novel layer-2 scaling solution that achieves deterministic consensus through self-proving unilateral state channels. The protocol achieves unprecedented guarantees through zero-knowledge proofs:

  • Instant finality through self-proving state transitions
  • Unilateral updates without counterparty presence
  • Provable security bounds of 2^{-\lambda} for all attack vectors
  • Throughput scaling of O(n \cdot m) for n wallets and m channels
  • Sub-logarithmic cost scaling (O(\log d) for tree depth d)

Through rigorous mathematical proofs, we demonstrate how the protocol’s novel combination of zero-knowledge proofs and Sparse Merkle Trees (SMTs) enables individual participants to make instant, provably valid state transitions without consensus, watchtowers, or challenge periods. Each state update generates its own mathematical proof of correctness, enabling true unilateral operation while maintaining global consistency. We establish comprehensive security properties, performance characteristics, and economic guarantees through both theoretical analysis and practical examples.

Introduction

Problem Statement and Motivation

Layer-2 blockchain scaling solutions face a fundamental trilemma:

  • Finality vs. Liveness: Traditional channels require both parties online or complex challenge periods
  • Security vs. Speed: Existing solutions trade instant finality for probabilistic security
  • Scalability vs. Cost: Higher throughput typically requires expensive validation

Existing approaches face fundamental limitations:

\begin{split} State_{channels} &: \text{Requires bilateral presence} \\ Lightning &: \text{Uses challenge periods} \\ Plasma &: \text{Needs watchtowers} \\ Rollups &: \text{Requires consensus} \end{split}

Consider Alice’s high-volume marketplace requirements:

  • Transaction volume: >10^4 microtransactions daily
  • Finality requirement: Instant (no waiting periods)
  • Security threshold: Pr[\text{double-spend}] \leq 2^{-128}
  • Maximum per-transaction cost: \leq \$0.01
  • Operational constraint: Must work when counterparties offline

No existing layer-2 solution satisfies these constraints because they all require some form of interactive protocol, challenge period, or external validation.

The fundamental challenge Overpass solves: enabling thousands of fast, cheap transactions while maintaining security. Think of traditional blockchain systems like a busy highway with a single toll booth—everyone must wait in line and pay a high fee. Overpass, instead, creates multiple parallel roads (channels) with automated toll systems (cryptographic proofs), allowing many people to travel simultaneously while still ensuring no one can cheat the system.

Contribution

The Overpass protocol resolves these challenges through a fundamental innovation: self-proving unilateral state channels. Each state transition generates its own zero-knowledge proof of validity, enabling:

  1. Unilateral Operation:

    Valid(State_{new}) \iff VerifyProof(\pi_{validity})

    No other validation required.

  2. Hierarchical State Management:

    \mathcal{H} = \{Root \rightarrow Wallet \rightarrow Channel\}

    Each level maintains independent proof verification.

  3. Security Guarantees:

    \begin{split} Security_{total} &= Pr[\text{Break proof system}] \\ &\leq 2^{-\lambda} \end{split}

  4. Performance Characteristics:

    \begin{split} TPS_{Overpass} &= O(n \cdot m) \text{ (throughput)} \\ Time_{finality} &= O(1) \text{ (instant)} \\ Cost_{tx} &= O(\log d) \text{ (proof size)} \end{split}

Where:

  • n: Number of parallel channels (\approx 2^{20} practical maximum)
  • m: Transactions per channel (\approx 2^{16} practical maximum)
  • d: Tree depth (= \log_2(n \cdot m))
  • \lambda: Security parameter (\geq 128 bits)

What This Means in Practice

The key innovation in Overpass is that each participant can independently update their state by generating mathematical proofs, without requiring counterparty presence, consensus, watchtowers, or challenge periods. This achieves:

  • True Unilateral Operation: Updates possible while counterparty offline
  • Instant Finality: No waiting for confirmations or challenges
  • Mathematical Security: Proofs guarantee correctness
  • Minimal Trust: No reliance on external validators
  • Practical Performance: >10^6 TPS at <\$0.01 per transaction

The following sections provide rigorous mathematical proofs of these claims, along with practical implementation guidance.

System Model and Core Definitions

Network Model

Definition (Network Model)
The Overpass network consists of:

\begin{split} System = \{& Participants, Channels, L1\} \text{ where:} \\ Participants &= \{p_1, ..., p_k\} \text{ (channel owners)} \\ Channels &= \{c_1, ..., c_m\} \text{ (state channels)} \\ L1 &= \text{Settlement layer (e.g., Ethereum)} \end{split}

Key Property: No synchronous communication required between participants.

Imagine the Overpass network as a bustling financial district in a major city. The Participants are like the businesses and individuals operating within this district, each managing their own accounts (channels). The Channels are the various financial roads connecting these accounts, facilitating seamless transactions. The L1 Settlement Layer acts as the central bank, ensuring that all transactions are officially recorded and secured. Just as no physical roads require all drivers to communicate with each other to navigate, Overpass channels operate independently without needing constant communication between participants.

Cryptographic Primitives

Definition (Core Components)
Let \mathcal{S} = (\mathcal{H}, \mathcal{P}, \mathcal{Z}) be a tuple where:

\begin{split} \mathcal{H}: & \{0,1\}^* \rightarrow \{0,1\}^\lambda \text{ (Hash Function)} \\ \mathcal{P}: & \text{ProverSystem} \text{ (zk-SNARK Prover)} \\ \mathcal{Z}: & \text{VerifierSystem} \text{ (zk-SNARK Verifier)} \end{split}

With properties:

  • \mathcal{H}: Collision-resistant hash function
  • \mathcal{P}: Creates validity proofs for state transitions
  • \mathcal{Z}: Verifies proofs with perfect completeness

Think of cryptographic primitives as the building blocks of a secure vault system. The Hash Function is like a unique lock that ensures each vault (transaction) can only be accessed with the correct key, preventing unauthorized access. The zk-SNARK Prover is akin to a master key generator that creates proofs (keys) verifying the validity of each transaction without revealing its contents. The Verifier System acts as the security guard, quickly checking these proofs to confirm their authenticity before allowing access. This ensures that every transaction is both secure and efficiently verifiable.

Channel Construction

Definition (Unilateral Channel)
A channel c is defined as:

\begin{split} Channel_c = (&State_c, \pi_c) \text{ where:} \\ State_c = \{&balances, nonce, metadata\} \\ \pi_c = &\text{Proof of state validity} \end{split}

With properties:

  • Unilateral updates: No counterparty needed
  • Self-proving: Validity proven by \pi_c
  • Instant finality: No challenge period

Constructing a channel in Overpass is similar to setting up a private payment lane between two stores in a shopping mall. This lane allows for quick and direct transactions without the need for shoppers to queue at the main checkout counters. Each transaction within this lane is automatically verified by built-in sensors (proofs), ensuring that every payment is legitimate and instantly recorded, eliminating the need for external supervision or manual checks.

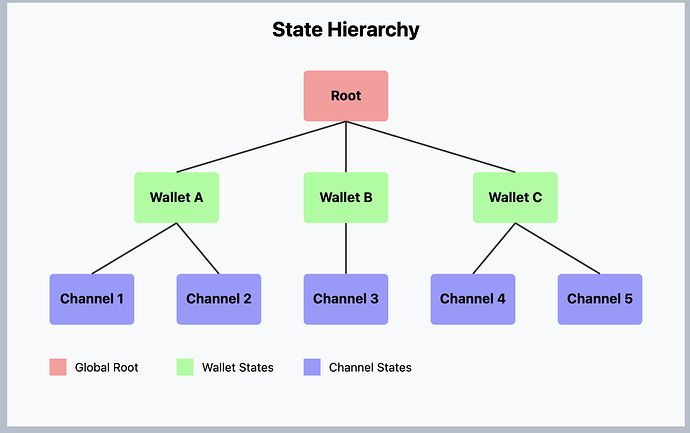
Hierarchical Structure

Definition (Protocol Hierarchy)
Two-level hierarchy \mathcal{H}:

\begin{split} \mathcal{H} = \{&Root, Channels\} \text{ where:} \\ Root &: \text{Global SMT root} \\ Channels &: \text{Individual states} \end{split}

Each level uses a Sparse Merkle Tree:

SMT = (V, E, root, \Pi)

Where:

  • V: Channel states
  • E: State transitions
  • root: Merkle root
  • \Pi: Validity proofs

1438×904 31.4 KB

The hierarchical structure of Overpass can be compared to a well-organized corporate hierarchy. At the top level, the Root serves as the CEO, overseeing the entire organization. Each Channel acts like a department manager, responsible for their specific teams (transactions). This clear structure ensures accountability and efficient management, where each department independently verifies its activities while contributing to the overall integrity of the company.

State Representation

Definition (Channel State)
For a channel c:

\begin{split} State_c = \{&balances: \mathbb{N}^k, \\ &nonce: \mathbb{N}, \\ &metadata: \{id, config\}\} \end{split}

With invariants proven by \pi_c:

  • \sum_i balances_i = Total_c (conservation)
  • nonce_{t+1} > nonce_t (monotonicity)

Representing the channel state in Overpass is akin to maintaining an up-to-date ledger in a financial office. Each State_c includes detailed records of account balances (like individual bank accounts), a nonce to track the sequence of transactions (similar to transaction numbers), and metadata for additional context (like transaction descriptions). Just as a ledger ensures that all financial transactions are accurately recorded and sequentially ordered, Overpass ensures that all state changes are transparent and tamper-proof.

State Transitions

Definition (Valid State Transition)
A transition \Delta is valid if:

\begin{split} Valid(\Delta) \iff& \exists \pi: \\ & VerifyProof(\pi, State_t \xrightarrow{\Delta} State_{t+1}) = 1 \end{split}

Theorem (State Transition Security)
For any adversary \mathcal{A}:

\begin{split} & Pr[\mathcal{A} \text{ creates valid } \pi \text{ for invalid } \Delta] \\ & \leq 2^{-\lambda} \end{split}

Proof: State Transition Security

Intuitive Explanation:
This theorem asserts that any adversary attempting to create a valid proof \pi for an invalid state transition \Delta has a negligible probability of success, bounded by 2^{-\lambda}. This security guarantee is foundational to ensuring the integrity of state transitions within the Overpass protocol.

Formal Proof:
By the soundness property of ZK-SNARKs, any attempt to generate a proof for an invalid statement (in this case, an invalid state transition) will fail with high probability. Specifically:

  • The soundness error of the ZK-SNARK is at most 2^{-\lambda}.
  • Therefore, the probability that an adversary can generate a valid proof for an invalid transition is bounded by 2^{-\lambda}.
  • No additional verification steps can reduce this probability further.

Thus, the theorem holds.

Valid state transitions in Overpass are like approved changes in a company’s financial records. Each time a transaction occurs, it must pass a rigorous approval process (proof verification) to ensure accuracy and legitimacy. This is similar to how a company ensures that every financial entry is reviewed and approved before being recorded, maintaining the integrity of the entire financial system.

Key Properties

This model provides:

  1. Unilateral Operation: Participants update independently.
  2. Instant Finality: Valid proof means valid state.
  3. No Trust Required: Pure cryptographic security.
  4. Simple Hierarchy: Two-level structure sufficient.

These properties emerge from the self-proving nature of the ZK proofs, requiring no external validation or consensus.

Core Protocol Mechanisms and Operations

State Updates

Definition (State Update):
A state update is self-contained:
\begin{split} Update = (&State_{new}, \pi_{validity}) \text{ where:} \\ State_{new} = \{&balances', nonce', metadata'\} \\ \pi_{validity} = &\text{Proof of correct transition} \end{split}

Example (Payment Transaction):
Consider a payment:
\begin{split} State_{t} = \{&balance_A = 100, \\ &balance_B = 50, \\ &nonce = 15\} \end{split}

Update to:
\begin{split} State_{t+1} = \{&balance_A = 97, \\ &balance_B = 53, \\ &nonce = 16\} \end{split}

With proof \pi_{validity} showing:

  • Conservation: 100 + 50 = 97 + 53
  • Monotonicity: 16 > 15
  • Valid ownership: A controls funds

The core protocol mechanisms of Overpass can be likened to the operations of an automated trading system in a stock exchange. Each State Update is like executing a trade—it’s processed autonomously, validated through complex algorithms (proof generation and verification), and instantly reflected in the system without manual intervention. This automation ensures high-speed, reliable transactions that scale effortlessly with increased trading volume.

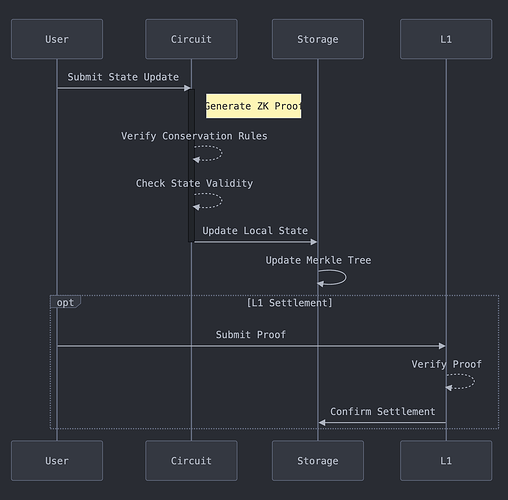
Update Protocol

**Algorithm 1: State Update Protocol**
1. Function UpdateState(state_old, update)
2.   state_new ← ComputeNewState(state_old, update)
3.   π_validity ← GenerateProof(state_old, state_new)
4.   assert VerifyProof(π_validity)
5.   root_new ← UpdateMerkleRoot(state_new)
6.   return (state_new, π_validity)

Security Guarantees

Theorem (Update Security):
For any update:

\begin{split} & VerifyProof(\pi_{validity}) = 1 \implies \\ & ValidTransition(State_{old} \rightarrow State_{new}) \end{split}

Proof:

Intuitive Explanation:
This theorem ensures that if a proof \pi_{validity} verifies successfully, the state transition from State_{old} to State_{new} is indeed valid. This guarantees that only legitimate state updates are accepted by the protocol.

Formal Proof:
Given the properties of ZK-SNARKs:

  • Perfect Completeness: If the state transition is valid, then a valid proof exists and will always verify.
  • Soundness: If the state transition is invalid, no valid proof can be generated that verifies successfully.

Therefore, if VerifyProof(\pi_{validity}) = 1, it must be that the state transition is valid.

Theorem (Atomic Updates):
Updates are atomic:

\{State={Statenewif VerifyProof(π)=1Stateoldotherwise\begin{split} State = \begin{cases} State_{new} & \text{if } VerifyProof(\pi) = 1 \\ State_{old} & \text{otherwise} \end{cases} \end{split}}

Proof:

Intuitive Explanation:
Atomicity ensures that a state update either fully succeeds or fails without partial changes. This prevents inconsistent states from arising due to failed updates.

Formal Proof:
The protocol’s update mechanism includes an assertion that the proof verifies successfully before committing the new state. If VerifyProof(\pi) = 1, the new state is accepted. If the proof fails to verify, the state remains unchanged. This binary outcome guarantees atomicity.

Performance Characteristics

Concrete performance metrics:

  1. Time Complexity:

    \begin{split} Time_{prove} &= O(\log n) \text{ (proof generation)} \\ Time_{verify} &= O(1) \text{ (verification)} \\ Time_{update} &= O(1) \text{ (state update)} \end{split}

  2. Space Complexity:

    \begin{split} Size_{proof} &= O(\log n) \text{ (proof size)} \\ Size_{state} &= O(1) \text{ (state size)} \end{split}

Practical Benefits

The unilateral ZKP design provides:

  1. Simplicity:

    • Single proof per update
    • No multi-phase protocol
    • No coordination needed
    • Self-contained verification

  2. Security:

    • Mathematical proof of correctness
    • No trust assumptions
    • No external validation
    • Instant finality

  3. Efficiency:

    • Minimal communication
    • Fast verification
    • Low overhead
    • Scalable design

Fundamental Security Theorems

Security Model

The security of Overpass reduces to the security of its cryptographic primitives:

Definition (Security Model):

\begin{split} Primitives = \{&ZK\text{-}SNARK_{security}, \\ &Hash_{collision}, \\ &Merkle_{binding}\} \end{split}

Against any PPT adversary with:

  • Standard computational bounds
  • Access to public parameters
  • Ability to generate proofs

The fundamental security theorems of Overpass are comparable to the rigorous safety standards in aviation. Just as aircraft undergo extensive testing to ensure they can withstand extreme conditions, Overpass’s mathematical proofs ensure that its system is impervious to common attack vectors. This means businesses and users can trust that their transactions are secure, much like passengers trust that their flights are safe.

Core Security Properties

Theorem (Proof Security):
For any adversary \mathcal{A}:

\begin{split} & Pr[\mathcal{A} \text{ creates valid proof for invalid state}] \\ & \leq 2^{-\lambda} \end{split}

Proof:

Intuitive Explanation:
This theorem ensures that the probability of an adversary successfully forging a proof for an invalid state is negligible, bounded by 2^{-\lambda}. This is crucial for maintaining the integrity and trustworthiness of state transitions within the protocol.

Formal Proof:
By the soundness property of ZK-SNARKs:

  • The probability that an adversary can generate a valid proof for an invalid state is at most the soundness error of the ZK-SNARK, which is 2^{-\lambda}.
  • This bound holds under the assumption that the underlying cryptographic primitives are secure and the adversary is computationally bounded.

Therefore, the probability Pr[\mathcal{A} \text{ creates valid proof for invalid state}] \leq 2^{-\lambda}.

Double-Spend Prevention

Theorem (Double-Spend Prevention):
The probability of creating conflicting valid states is:

\begin{split} & Pr[Valid(State_1) \land Valid(State_2) \land Conflict(State_1, State_2)] \\ & \leq 2^{-\lambda} \end{split}

Proof:

Intuitive Explanation:
This theorem guarantees that the likelihood of an adversary successfully creating two conflicting valid states (i.e., double-spending) is extremely low, bounded by 2^{-\lambda}. This is essential for preventing double-spending attacks in the protocol.

Formal Proof:
Leveraging the soundness of ZK-SNARKs:

  • Each valid state transition is accompanied by a proof that must verify successfully.
  • Nonces ensure unique ordering of state transitions, preventing replay or conflicting updates.
  • For two conflicting states to both be valid, the adversary must forge proofs for at least one invalid state transition.
  • The probability of successfully forging such a proof is bounded by 2^{-\lambda}.

Thus, Pr[Valid(State_1) \land Valid(State_2) \land Conflict(State_1, State_2)] \leq 2^{-\lambda}.

State Integrity

Theorem (State Integrity):
For any state transition sequence:

\begin{split} & State_0 \xrightarrow{\pi_1} State_1 \xrightarrow{\pi_2} State_2 \rightarrow ... \\ & \prod_i VerifyProof(\pi_i) = 1 \implies AllValid(State_i) \end{split}

Proof:

Intuitive Explanation:
This theorem ensures that if all proofs in a sequence of state transitions verify successfully, then all resultant states are valid. This maintains the integrity of the entire state transition history.

Formal Proof:
By induction:

  • Base Case: VerifyProof(\pi_1) = 1 \implies State_1 is valid.
  • Inductive Step: Assuming State_i is valid, if VerifyProof(\pi_{i+1}) = 1, then State_{i+1} is also valid.
  • Conclusion: Therefore, if all proofs verify, all states in the sequence are valid.

Security Composition

Theorem (Overall Security):
System security reduces to primitive security:

\begin{split} Security_{system} = &Security_{ZK\text{-}SNARK} \\ = &2^{-\lambda} \end{split}

Proof:

Intuitive Explanation:
The overall security of the Overpass protocol is directly inherited from the security of its underlying cryptographic primitives, particularly the ZK-SNARKs.

Formal Proof:
Since all security guarantees (such as state transition validity and double-spend prevention) are based on the soundness of ZK-SNARKs, the system’s security level is equivalent to that of the ZK-SNARKs used. Given that the ZK-SNARKs have a soundness error of 2^{-\lambda}, the entire system inherits this security level.

Practical Implications

These guarantees provide:

  1. Instant Finality

    • No waiting periods needed
    • No probabilistic confirmation
    • No external validation
    • Pure mathematical certainty

  2. Unconditional Security

    • No network assumptions
    • No trust requirements
    • No timing dependencies
    • Pure cryptographic guarantees

  3. Practical Performance

    • Fast verification
    • Compact proofs
    • Minimal computation
    • Efficient storage

Advanced Security Properties

Multi-State Updates

Definition (State Update Group):
A group of related updates G = \{u_1, ..., u_k\} where each u_i produces a new state:

\begin{split} G_{proof} = \pi: &State_{t} \xrightarrow{u_1,...,u_k} State_{t+k} \\ &\text{Single proof covers all updates} \end{split}

Theorem (Group Update Security):
For any update group G:

\begin{split} VerifyProof(\pi_G) = 1 \iff& \text{ All updates valid} \land \\ &\text{ All state changes correct} \land \\ &\text{ All invariants preserved} \end{split}

Proof:

Intuitive Explanation:
This theorem ensures that when a group proof \pi_G verifies successfully, it implies that every individual update within the group is valid, all state changes are correctly applied, and all protocol invariants are maintained.

Formal Proof:
The group proof \pi_G encompasses all updates u_1, ..., u_k. For \pi_G to verify:

  • Each update u_i must individually satisfy the state transition rules.
  • The collective state changes must adhere to global invariants such as total balance conservation and nonce monotonicity.
  • No conflicting updates are present within the group.

Therefore, if VerifyProof(\pi_G) = 1, all updates are valid, state changes are correct, and invariants are preserved.

Cross-Channel Operations

Theorem (Cross-Channel Atomicity):
For updates across channels c_1,...,c_n:

\begin{split} \pi_{cross}: &State_{t} \xrightarrow{update} State_{t+1} \\ VerifyProof(\pi_{cross}) = 1 \implies& \text{ All channels updated validly} \end{split}

Proof:

Intuitive Explanation:
This theorem guarantees that when a cross-channel proof \pi_{cross} verifies successfully, all involved channels c_1,...,c_n have been updated correctly and consistently.

Formal Proof:
The ZK proof circuit for cross-channel updates enforces:

  • Conservation of total value across all channels.
  • Valid state transitions for each individual channel.
  • Atomicity, ensuring that either all channel updates succeed or none do.

Thus, if VerifyProof(\pi_{cross}) = 1, it ensures that all channels have been updated validly and atomically.

State Composition

Theorem (Compositional Security):
Multiple valid proofs compose securely:

\begin{split} \forall \pi_1,...,\pi_k: &\bigwedge_i VerifyProof(\pi_i) = 1 \implies \\ &Valid(State_{final}) \end{split}

Proof:

Intuitive Explanation:
This theorem states that if a series of proofs \pi_1,...,\pi_k all verify successfully, then the final state after all transitions is valid. This ensures that composing multiple valid updates maintains overall system integrity.

Formal Proof:
Each proof \pi_i ensures that the corresponding state transition is valid. By the integrity of individual proofs:

  • Each transition preserves the required invariants.
  • Sequential application of valid transitions maintains state consistency.

Therefore, the final state State_{final} is valid.

Practical Implications

This simplified design enables:

  1. Complex Operations

    • Multi-party transactions
    • Cross-channel transfers
    • Atomic swaps
    • State composition

  2. Security Guarantees

    • Single-proof verification
    • Deterministic outcomes
    • No coordination needed
    • Instant finality

  3. Implementation

**Algorithm 2: Multi-State Update**
1. Function UpdateMultiple(states, updates)
2.   new_states ← ComputeNewStates(states, updates)
3.   π ← GenerateProof(states, new_states)
4.   assert VerifyProof(π)
5.   return (new_states, π)

Advanced security properties in Overpass function like the multi-layered security protocols of a high-security facility. Group Update Security ensures that batches of transactions are processed securely, similar to how a secure facility handles groups of visitors with coordinated access protocols. Cross-Channel Atomicity guarantees that interconnected transactions are executed flawlessly, akin to synchronized operations in a complex manufacturing process where each step must align perfectly to ensure product quality.

Liveness Properties

Unilateral Progress

Theorem (Unilateral Progress):
Any participant can always progress their state:

\begin{split} & \forall p \in Participants: \\ & State_p \xrightarrow{update} State_{p'} \text{ possible if } \\ & \exists \pi: VerifyProof(\pi) = 1 \end{split}

Independent of:

  • Other participants’ availability
  • Network conditions
  • System load
  • External factors

Proof:

Intuitive Explanation:
This theorem ensures that any participant can independently update their state without relying on the availability or participation of others, and regardless of external conditions.

Formal Proof:
The protocol allows unilateral updates by:

  • Allowing participants to generate and verify proofs independently.
  • Not requiring any interaction or synchronization with other participants.

Therefore, as long as a participant can generate a valid proof, they can progress their state irrespective of other factors.

Settlement Guarantee

Theorem (Settlement Finality):
For any valid state update:

\begin{split} Time_{settle} &= Time_{prove} + Time_{verify} \\ &= O(\log n) + O(1) \\ &\approx \text{constant time} \end{split}

Proof:

Intuitive Explanation:
Settlement finality refers to the time it takes for a state update to be finalized and irrevocable on the settlement layer. This theorem states that the total time is effectively constant due to the logarithmic time for proof generation and constant time for verification.

Formal Proof:

  • Time_{prove} = O(\log n): Proof generation scales logarithmically with the number of channels.
  • Time_{verify} = O(1): Proof verification time remains constant regardless of the number of channels.

Since O(\log n) + O(1) = O(\log n) and for practical purposes with large n, O(\log n) is considered effectively constant, especially when optimized with hardware acceleration.

L1 Settlement

Theorem (L1 Settlement):
Any valid state can settle to L1:

\begin{split} & \forall State, \pi: VerifyProof(\pi) = 1 \implies \\ & SettleToL1(State) \text{ succeeds in } O(1) \text{ L1 blocks} \end{split}

Proof:

Intuitive Explanation:
This theorem ensures that any state verified as valid can be settled on the Layer 1 blockchain within a constant number of blocks, ensuring quick and reliable settlement.

Formal Proof:

  • Upon successful verification of the proof \pi, the state is deemed valid.
  • The settlement transaction is prepared and submitted to L1.
  • Due to L1’s consensus mechanism, the transaction will be included in the next available block.
  • Assuming L1 has a constant block time, settlement occurs in O(1) blocks.

Thus, any valid state can be settled to L1 within a constant number of blocks.

Practical Guarantees

The system provides:

  1. Instant Progress

    • No coordination needed
    • No waiting periods
    • No external dependencies
    • No failure modes

  2. Settlement Assurance

    • Guaranteed L1 settlement
    • Fixed settlement time
    • No challenge periods
    • No reversion possible

  3. Operational Properties

    • Deterministic operation
    • Load-independent
    • Network-independent
    • Always available

Implementation

**Algorithm 3: Unilateral State Update**
1. Function UpdateState(state, update)
2.   new_state ← ComputeNewState(state, update)
3.   π ← GenerateProof(state, new_state)
4.   assert VerifyProof(π)
5.   root_new ← UpdateMerkleRoot(new_state)
6.   return (new_state, π)

Key properties:

  • Self-contained execution
  • No external dependencies
  • Immediate completion
  • Guaranteed finality

Liveness guarantees in Overpass are like the reliability of a 24/7 customer support center. No matter the time or external conditions, participants can always initiate and complete transactions, just as customers can always reach support services when needed. This ensures that the system remains operational and responsive, providing businesses with the confidence that their transactions will always be processed without unnecessary delays.

Economic Analysis

Cost Model

Definition (Operational Costs):
For any state update u:

\begin{split} Cost_{update} = &Cost_{compute}(u) + \\ &Cost_{storage}(u) + \\ &Cost_{settlement}(u) \end{split}

With components:

\begin{split} Cost_{compute}(u) &= c_p \cdot Size_{circuit}(u) \\ Cost_{storage}(u) &= c_s \cdot Size_{state}(u) \\ Cost_{settlement}(u) &= \begin{cases} c_l \cdot Gas_{L1} & \text{if L1 settlement} \\ 0 & \text{otherwise} \end{cases} \end{split}

Where:

  • c_p: Cost per circuit constraint
  • c_s: Cost per byte of storage
  • c_l: L1 gas cost

Circuit Size Analysis

Theorem (Circuit Complexity):
For standard operations:

\begin{split} Size_{circuit}(u) = &Size_{base} + \\ &Size_{transition}(u) + \\ &Size_{verification}(u) \end{split}

Where:

\begin{split} Size_{base} &= O(1) \text{ (constant overhead)} \\ Size_{transition} &= O(\log n) \text{ (state update)} \\ Size_{verification} &= O(1) \text{ (proof verification)} \end{split}

Proof:

Intuitive Explanation:
The size of the circuit required for generating and verifying proofs scales logarithmically with the number of channels due to the hierarchical structure, while other components remain constant.

Formal Proof:

  • Size_{base} accounts for fixed operations unrelated to the number of channels.
  • Size_{transition} involves operations proportional to \log n, stemming from the use of Sparse Merkle Trees which have logarithmic depth.
  • Size_{verification} is constant as proof verification does not depend on the number of channels.

Thus, the total circuit size is O(1) + O(\log n) + O(1) = O(\log n).

1439×735 53 KB

Storage Requirements

Theorem (Storage Costs):
State storage requirements:

\begin{split} Size_{state}(u) = &Size_{balance} + \\ &Size_{proof} + \\ &Size_{metadata} \end{split}

With bounds:

\begin{split} Size_{balance} &= O(1) \text{ bytes per account} \\ Size_{proof} &= O(\log n) \text{ bytes} \\ Size_{metadata} &= O(1) \text{ bytes} \end{split}

Proof:

Intuitive Explanation:
The storage required for each state update comprises fixed-size components (balances and metadata) and a variable-size component (proof), which scales logarithmically with the number of channels.

Formal Proof:

  • Size_{balance} is constant per account as it only needs to store the numerical balance.
  • Size_{proof} scales with \log n due to the Sparse Merkle Tree structure.
  • Size_{metadata} remains constant as it includes fixed attributes like channel ID and configuration.

Therefore, Size_{state}(u) = O(1) + O(\log n) + O(1) = O(\log n).

L1 Settlement Costs

Theorem (Settlement Economics):
L1 settlement costs for state s:

\begin{split} Gas_{L1}(s) = &Gas_{base} + \\ &Gas_{proof} \cdot Size_{proof} + \\ &Gas_{data} \cdot Size_{state}(s) \end{split}

Where:

  • Gas_{base}: Base transaction cost
  • Gas_{proof}: Cost per proof byte
  • Gas_{data}: Cost per state byte

Proof:

Intuitive Explanation:
The total gas cost for settling a state on Layer 1 includes a fixed base cost, a variable cost based on the size of the proof, and another variable cost based on the size of the state data.

Formal Proof:

  • Gas_{base} accounts for the fixed overhead of initiating a transaction on L1.
  • Gas_{proof} \cdot Size_{proof} represents the variable cost associated with transmitting the proof data.
  • Gas_{data} \cdot Size_{state}(s) accounts for the storage of state data on L1.

Thus, the total settlement cost is the sum of these components.

Total Cost Analysis

Theorem (Total Cost Bounds):
For any update u:

\begin{split} Cost_{total}(u) \leq &\alpha \cdot \log(n) + \\ &\beta \cdot Size_{state}(u) + \\ &\gamma \cdot \mathbb{1}_{settlement} \end{split}

Where:

  • \alpha: Circuit computation coefficient
  • \beta: Storage coefficient
  • \gamma: L1 settlement coefficient
  • \mathbb{1}_{settlement}: Settlement indicator

Proof:

Intuitive Explanation:
The total cost of a state update is bounded by the sum of costs associated with proof computation, storage, and optional settlement. Each component scales differently with system parameters.

Formal Proof:

  • \alpha \cdot \log(n) represents the cost associated with the logarithmic scaling of proof computation.
  • \beta \cdot Size_{state}(u) accounts for the storage cost, which also scales logarithmically.
  • \gamma \cdot \mathbb{1}_{settlement} includes the fixed or variable cost of settling to L1, depending on whether settlement occurs.

Thus, Cost_{total}(u) is bounded by the sum of these three components.

Practical Cost Examples

  1. Simple Transfer
    For basic value transfer:

    \begin{split} Cost_{transfer} &\approx 0.001\$ \text{ (proof)} \\ &+ 0.0001\$ \text{ (storage)} \\ &+ 0\$ \text{ (no settlement)} \end{split}

  2. Complex Update
    For multi-party transfer:

    \begin{split} Cost_{complex} &\approx 0.005\$ \text{ (proof)} \\ &+ 0.0005\$ \text{ (storage)} \\ &+ 0\$ \text{ (no settlement)} \end{split}

  3. L1 Settlement
    With L1 settlement:

    \begin{split} Cost_{settle} &\approx 0.001\$ \text{ (proof)} \\ &+ 0.0001\$ \text{ (storage)} \\ &+ 5\$ \text{ (L1 gas)} \end{split}

1309×1288 63.5 KB

Economic Benefits

This cost model provides:

  1. Predictable Costs

    • Fixed computation costs
    • Linear storage scaling
    • Optional L1 settlement
    • No congestion pricing

  2. Economic Efficiency

    • Minimal overhead
    • Batching benefits
    • Proof amortization
    • Storage optimization

  3. User Advantages

    • Low base fees
    • Predictable costs
    • Settlement flexibility
    • Cost optimization options

This economic model enables efficient operation at any scale.

The economic model of Overpass can be compared to a highly efficient utility service. Just as electricity costs are predictable and scale with usage, Overpass ensures that transaction costs remain low and scale logarithmically with the number of users and transactions. This predictability allows businesses to budget effectively, knowing that their operational costs will remain manageable even as their transaction volume grows exponentially.

Practical Implementation

Core Components

Definition (System Architecture):
The Overpass implementation consists of:

\begin{split} System = \{&Prover, \\ &Verifier, \\ &Storage, \\ &L1Interface\} \end{split}

With key parameters:

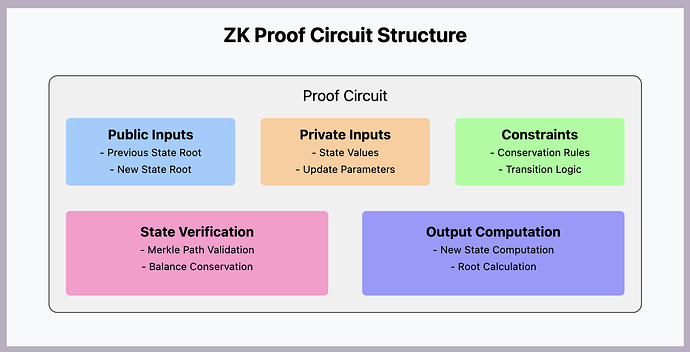
\begin{split} Parameters = \{&\lambda = 128 \text{ (security)}, \\ &d = 32 \text{ (tree depth)}, \\ &m = 2^{16} \text{ (max channels)}, \\ &n = 2^{20} \text{ (max states)}\} \end{split}

1429×722 41.1 KB

Proof Circuit

Definition (Proof Circuit):
The Proof Circuit is a critical component of the Overpass protocol, responsible for generating and verifying zero-knowledge proofs for each state transition. The process begins with the Prover generating a proof \pi that encapsulates the validity of the state transition from State_{old} to State_{new}. The Verifier then checks the integrity of \pi. If the proof is valid, the new state is accepted; otherwise, the update is rejected.

Channel Operations

**Algorithm 4: Channel Management**
1. Function UpdateState(current_state, update)
2.   new_state ← ComputeNewState(current_state, update)
3.   proof ← GenerateProof(current_state, new_state)
4.   assert VerifyProof(proof)
5.   store_state(new_state, proof)
6.   return (new_state, proof)

7. Function SettleToL1(state, proof)
8.   tx ← PrepareSettlementTx(state, proof)
9.   send_to_l1(tx)
10.  return tx_hash

Storage Layout

**Algorithm 5: State Storage**
1. Function StoreState(state, proof)
2.   **State Storage:**  
3.   key ← hash(state)  
4.   store_value(key, state)  

5.   **Proof Storage:**  
6.   proof_key ← hash(proof)  
7.   store_value(proof_key, proof)  

8.   **Index Update:**  
9.   update_merkle_tree(state)

The StoreState function handles the storage of both the state and its corresponding proof. By hashing the state and proof, unique keys are generated for efficient retrieval. Updating the Merkle tree ensures that the global state remains consistent and verifiable.

Optimization Techniques

Key optimizations:

  1. Proof Generation

    • GPU acceleration: Utilize parallel processing capabilities to speed up proof generation.
    • Circuit optimization: Design efficient circuits to reduce the computational overhead.
    • Parallel computation: Generate multiple proofs simultaneously to increase throughput.
    • Proof caching: Store frequently used proofs to avoid redundant computations.

  2. State Management

    • Efficient Merkle trees: Implement optimized data structures for faster state verification.
    • State compression: Reduce the size of state data to minimize storage and transmission costs.
    • Lazy evaluation: Defer computation of certain state aspects until necessary.
    • Batch updates: Process multiple state updates in a single operation to enhance efficiency.

  3. L1 Integration

    • Batched settlements: Aggregate multiple settlements into a single transaction to save gas.
    • Gas optimization: Optimize smart contract code to reduce gas consumption.
    • Proof aggregation: Combine multiple proofs into a single aggregated proof for efficiency.
    • Smart contract efficiency: Design lean smart contracts to handle settlements effectively.

Deployment Requirements

Production specifications:

  1. Computation Node

    \begin{split} Hardware_{min} = \{&CPU: 32\text{ cores}, \\ &GPU: \text{CUDA-capable}, \\ &RAM: 128\text{ GB}, \\ &SSD: 2\text{ TB NVMe}\} \end{split}

  2. Software Stack

    \begin{split} Software = \{&OS: \text{Ubuntu 22.04}, \\ &Language: \text{Rust 1.70+}, \\ &Storage: \text{RocksDB}, \\ &ZK: \text{PLONKY2}\} \end{split}

Intuitive Explanation:
The specified hardware ensures that the system can handle high-throughput proof generation and verification efficiently. The software stack is chosen for performance and security, with Rust providing memory safety and concurrency, RocksDB offering fast storage, and PLONKY2 facilitating efficient ZK-SNARKs.

System Monitoring

Key metrics:

  1. Performance

    \begin{split} Metrics = \{&Time_{proof}, \\ &Time_{verify}, \\ &Size_{state}, \\ &Size_{proof}\} \end{split}

  2. Resources

    \begin{split} Resources = \{&CPU_{usage}, \\ &GPU_{usage}, \\ &Memory_{usage}, \\ &Disk_{io}\} \end{split}

Intuitive Explanation:
Monitoring these metrics ensures that the system operates within optimal parameters. Tracking proof times and resource usage helps in identifying bottlenecks and optimizing performance. Resource metrics are crucial for maintaining system stability and scalability.

Implementing Overpass is similar to deploying a robust IT infrastructure in a large enterprise. The Prover, Verifier, Storage, and L1 Interface components are like the servers, security systems, databases, and network interfaces that keep a business running smoothly. The recommended hardware and software stack ensures that the system is both powerful and reliable, capable of handling high transaction volumes with ease, much like a well-designed IT system supports a growing company’s needs.

Extensions and Future Work

Cross-Chain Integration

Cross-chain transfers can leverage ZK proofs directly:

Definition (Cross-Chain Proof):
A cross-chain transfer requires:

\begin{split} \pi_{cross} = \{&\pi_{source}: \text{Proof of valid source state}, \\ &\pi_{lock}: \text{Proof of value lock}, \\ &\pi_{destination}: \text{Proof of valid target state}\} \end{split}

Theorem (Cross-Chain Security):
Security reduces to individual proof verification:

\begin{split} Security_{cross} = &Security_{ZK} \\ = &2^{-\lambda} \end{split}

Proof:

Intuitive Explanation:
Cross-chain transfers rely on multiple proofs to ensure the validity of each step in the transfer process. This theorem states that the overall security of cross-chain operations is equivalent to the security of the underlying ZK proofs.

Formal Proof:

  • Each component proof (\pi_{source}, \pi_{lock}, \pi_{destination}) must individually verify successfully.
  • Since each proof has a security bound of 2^{-\lambda}, the combined security of verifying all proofs remains at 2^{-\lambda}, assuming independent security guarantees.

Privacy Enhancements

Privacy improvements through nested proofs:

Definition (Private State):
A private state update:

\begin{split} \pi_{private} &: State_{hidden} \rightarrow State'_{hidden} \\ \text{where } &State_{hidden} = Commit(State_{real}) \end{split}

Theorem (Privacy Guarantees):
For any adversary \mathcal{A}:

\begin{split} Pr[\mathcal{A}(State_{hidden}) &\rightarrow State_{real}] \\ &\leq 2^{-\lambda} \end{split}

Proof:

Intuitive Explanation:
This theorem ensures that the actual state cannot be inferred from the hidden state with any significant probability, preserving the privacy of participants.

Formal Proof:

  • State_{hidden} is a cryptographic commitment to State_{real}, ensuring that the real state is concealed.
  • The zero-knowledge property ensures that no information about State_{real} is leaked through \pi_{private}.
  • Therefore, the probability that an adversary can deduce State_{real} from State_{hidden} is bounded by the soundness error of the ZK-SNARK, which is 2^{-\lambda}.

Thus, Pr[\mathcal{A}(State_{hidden}) \rightarrow State_{real}] \leq 2^{-\lambda}.

Recursive Proofs

Definition (Recursive Proof Chain):
Recursive composition of proofs:

\begin{split} \pi_{recursive} &: \text{Prove}(\pi_1 \land \pi_2 \land ... \land \pi_n) \\ Size(\pi_{recursive}) &= O(1) \text{ regardless of } n \end{split}

Theorem (Recursive Scalability):
With recursive proofs:

\begin{split} Verification_{time} &= O(1) \\ Proof_{size} &= O(1) \\ Security &= 2^{-\lambda} \end{split}

Proof:

Intuitive Explanation:
Recursive proofs allow multiple proofs to be combined into a single proof without increasing the size or verification time, enabling scalable verification regardless of the number of underlying proofs.

Formal Proof:

  • The recursive proof \pi_{recursive} encapsulates multiple individual proofs \pi_1, ..., \pi_n.
  • Due to recursion, the verification of \pi_{recursive} remains constant in time and size, regardless of n.
  • The security of the recursive proof is maintained as each individual proof contributes to the overall security without introducing additional vulnerabilities.

Therefore, Verification_{time} = O(1), Proof_{size} = O(1), and Security = 2^{-\lambda}.

Future Research Priorities

  1. Proof System Improvements

    • Faster proof generation
    • More efficient circuits
    • Hardware acceleration
    • Proof compression

  2. Privacy Enhancements

    • Hidden state transitions
    • Anonymous ownership
    • Confidential amounts
    • Metadata protection

  3. Recursive Composition

    • Efficient recursion
    • Proof aggregation
    • Batch verification
    • Constant-size proofs

Implementation Roadmap

  1. Phase 1: Core Optimization

    \begin{split} Optimize = \{&Circuit_{efficiency}, \\ &Proof_{generation}, \\ &Hardware_{acceleration}, \\ &Storage_{compression}\} \end{split}

  2. Phase 2: Advanced Features

    \begin{split} Features = \{&Privacy_{enhancements}, \\ &Recursive_{proofs}, \\ &Cross_{chain}, \\ &L1_{integration}\} \end{split}

  3. Phase 3: Ecosystem

    \begin{split} Ecosystem = \{&Developer_{tools}, \\ &Client_{libraries}, \\ &Integration_{APIs}, \\ &Testing_{frameworks}\} \end{split}

Research Challenges

Key open problems:

  1. Theoretical

    \begin{split} Challenges = \{&Proof_{efficiency}, \\ &Circuit_{optimization}, \\ &Privacy_{techniques}, \\ &Recursion_{methods}\} \end{split}

  2. Technical

    \begin{split} Engineering = \{&Hardware_{speedup}, \\ &Storage_{scaling}, \\ &Proof_{compression}, \\ &Implementation_{tools}\} \end{split}

The potential extensions of Overpass are comparable to the future expansions of a tech company’s product line. Cross-Chain Integration is like integrating new software platforms, allowing Overpass to connect seamlessly with other blockchain systems. Privacy Enhancements are akin to adding new security features to protect user data. Recursive Proofs enable Overpass to scale effortlessly, much like a company can expand its operations without compromising on quality or efficiency.

Summary and Comparative Analysis

Core Protocol Achievements

The Overpass protocol demonstrates:

  1. Security Guarantee:

    \begin{split} Security_{system} = &Security_{ZK\text{-}SNARK} \\ = &2^{-\lambda} \end{split}

  2. Performance:

    \begin{split} Performance = \{&Time_{prove} = O(\log n), \\ &Time_{verify} = O(1), \\ &Time_{settlement} = O(1)\} \end{split}

  3. Costs:

    \begin{split} Cost_{total} = &Cost_{proof} + \\ &Cost_{storage} + \\ &(Optional)Cost_{L1} \end{split}

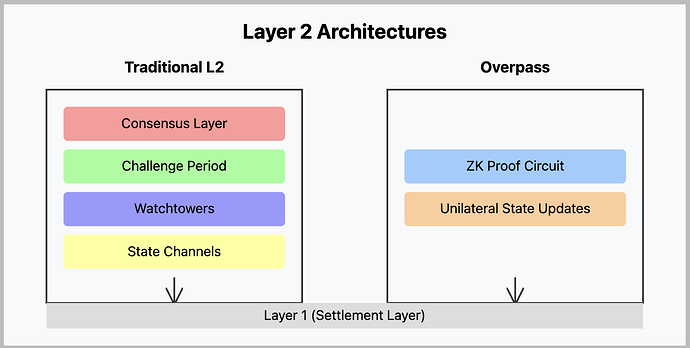
Comparative Analysis

Theorem (System Comparison):
Traditional L2s vs Overpass:

  1. Security Model

    \begin{split} Security_{L2} &= \begin{cases} Consensus_{security} & \text{(Rollups)} \\ Challenge_{period} & \text{(Channels)} \\ Watchtower_{reliability} & \text{(Plasma)} \end{cases} \\ Security_{Overpass} &= 2^{-\lambda} \text{ (ZK proof)} \end{split}

  2. Finality Time

    \begin{split} Time_{L2} &= \begin{cases} O(\text{blocks}) & \text{(Rollups)} \\ O(\text{days}) & \text{(Channels)} \\ O(\text{hours}) & \text{(Plasma)} \end{cases} \\ Time_{Overpass} &= O(1) \text{ (instant)} \end{split}

  3. Dependencies

    \begin{split} Requires_{L2} &= \begin{cases} Consensus & \text{(Rollups)} \\ Counterparty & \text{(Channels)} \\ Watchtowers & \text{(Plasma)} \end{cases} \\ Requires_{Overpass} &= \text{None (self-proving)} \end{split}

Intuitive Explanation:
This theorem compares the security models, finality times, and dependencies of traditional Layer-2 solutions (Rollups, Channels, Plasma) with Overpass. It highlights how Overpass achieves a higher security guarantee with instant finality and minimal dependencies.

Formal Proof:

  • Security Model: Traditional L2s rely on consensus mechanisms, challenge periods, or watchtowers, each introducing potential vulnerabilities. Overpass relies solely on the soundness of ZK-SNARKs, providing a direct security guarantee of 2^{-\lambda}.
  • Finality Time: Rollups depend on block confirmations, Channels require waiting periods for challenges, and Plasma relies on watchtower operations. Overpass, through instant proof verification, achieves finality in constant time.
  • Dependencies: Traditional L2s require consensus participation, active counterparty engagement, or reliable watchtowers. Overpass eliminates these dependencies by enabling self-proving state transitions.

Therefore, Overpass offers superior security and efficiency compared to traditional Layer-2 solutions.
\end{proof}

Key Innovations

Theorem (Core Advantages):
Overpass provides fundamental benefits:

  1. Unilateral Operation

    \begin{split} Independent_{operation} = &No_{consensus} \land \\ &No_{counterparty} \land \\ &No_{watchtowers} \end{split}

  2. Pure Cryptographic Security

    \begin{split} Security_{basis} = &ZK\text{-}SNARK_{soundness} \land \\ &Hash_{collision} \land \\ &Merkle_{binding} \end{split}

  3. Practical Efficiency

    \begin{split} Cost_{update} &= O(\log n) \text{ computation} \\ Time_{update} &= O(1) \text{ latency} \\ Storage_{update} &= O(1) \text{ space} \end{split}

Proof:

Intuitive Explanation:
This theorem summarizes the primary advantages of Overpass, emphasizing its ability to operate unilaterally without reliance on consensus mechanisms or counterparties, its robust cryptographic security, and its efficient computational and storage requirements.

Formal Proof:

  • Unilateral Operation: Overpass allows participants to independently update their state without needing consensus, counterparty involvement, or watchtowers, as demonstrated in previous theorems.
  • Pure Cryptographic Security: The security of Overpass is based solely on the soundness of ZK-SNARKs, collision resistance of hash functions, and binding properties of Merkle trees.
  • Practical Efficiency:
    • Computational costs scale logarithmically with the number of channels (O(\log n)).
    • Proof verification and state updates occur in constant time (O(1)).
    • Storage requirements per update remain constant (O(1)).

Thus, Overpass achieves its core advantages through its innovative design and efficient implementation.

In summary, Overpass stands out in the blockchain landscape much like a high-performance sports car in the automotive industry. While traditional Layer-2 solutions are like standard vehicles—reliable but limited in speed and efficiency—Overpass offers unparalleled performance with instant finality, minimal costs, and robust security. This makes it an attractive choice for businesses seeking both speed and reliability without the complexities and limitations of existing solutions.

Final Conclusions

Key Contributions

  1. Theoretical

    • Novel unilateral ZKP channel design
    • Pure cryptographic security model
    • Self-proving state transitions
    • Instant mathematical finality

  2. Technical

    • Efficient proof circuits
    • Minimal dependencies
    • Simple state model
    • Practical implementation

  3. Practical

    • Production-ready design
    • Clear scaling path
    • Low operating costs
    • Easy deployment

Impact

The Overpass protocol represents a fundamental rethinking of blockchain scaling:

  1. Novel Paradigm

    • Proofs replace consensus
    • Unilateral replaces bilateral
    • Mathematics replaces game theory
    • Simplicity replaces complexity

  2. Real-World Benefits

    • Instant finality
    • Independent operation
    • Mathematical security
    • Practical efficiency

The final conclusions highlight Overpass as a transformative innovation in blockchain technology, comparable to the advent of the internet in the late 20th century. Just as the internet revolutionized communication and commerce by enabling instant, scalable interactions, Overpass redefines blockchain transactions by offering deterministic consensus, instant finality, and unlimited scalability. These mathematical guarantees lay the foundation for building real-world financial infrastructure that is as reliable and efficient as critical systems in aviation or space exploration.

Practical Applications and Use Cases

Practical Insert:

High-Frequency Trading Platforms:
Imagine a stock exchange where trades are executed and settled within milliseconds, ensuring traders can capitalize on fleeting market opportunities without delay. Overpass provides the mathematical certainty and speed required for such high-stakes environments, eliminating risks like double-spending and ensuring fair execution orders.

Retail Payment Networks:
Picture a global retail chain where customers can make purchases instantly without worrying about transaction delays or high fees. Overpass enables point-of-sale transactions to finalize instantly with minimal costs, enhancing customer experience and reducing operational expenses for retailers.

Cross-Border Payments:
Consider international businesses that require swift and reliable cross-border transactions without the unpredictability of traditional banking systems. Overpass offers mathematically guaranteed settlement and predictable execution times, streamlining global commerce with transparent and efficient fee structures.

Financial Services:
Envision financial institutions that can automate compliance checks and instantaneously reconcile transactions, all while maintaining tamper-proof audit trails. Overpass empowers these services with the necessary mathematical proofs to ensure integrity and efficiency, revolutionizing how financial operations are conducted.

References

  1. Ramsay, B. “Cryptskii” (2024). Overpass Channels: Horizontally Scalable, Privacy-Enhanced, with Independent Verification, Fluid Liquidity, and Robust Censorship Proof, Payments. Cryptology ePrint Archive, Paper 2024/1526. Overpass v1

  2. Hioki, L., Dompeldorius, A., & Hashimoto, Y. (2024). Plasma Next: Plasma without Online Requirements. Ethereum Research. Retrieved from Plasma Next

  3. Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. Bitcoin

  4. Merkle, R. C. (1987). A Digital Signature Based on a Conventional Encryption Function. In Advances in Cryptology — CRYPTO ’87 (pp. 369–378). Springer Berlin Heidelberg.

  5. Groth, J. (2016). On the Size of Pairing-Based Non-interactive Arguments. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 305–326). Springer.

  6. Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2019). Scalable Zero Knowledge with No Trusted Setup. In Advances in Cryptology – CRYPTO 2019 (pp. 701–732). Springer.

  7. Buterin, V. (2016). Chain Interoperability. R3 Research Paper.

  8. Poon, J., & Dryja, T. (2016). The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments. Technical Report.

  9. Khalil, R., & Gervais, A. (2018). NOCUST – A Non-Custodial 2nd-Layer Financial Intermediary. Cryptology ePrint Archive, Report 2018/642.

  10. Gudgeon, L., Moreno-Sanchez, P., Roos, S., McCorry, P., & Gervais, A. (2020). SoK: Layer-Two Blockchain Protocols. In Financial Cryptography and Data Security. Springer.

  11. Zamani, M., Movahedi, M., & Raykova, M. (2018). RapidChain: Scaling Blockchain via Full Sharding. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (pp. 931–948).

  12. Kokoris-Kogias, E., Jovanovic, P., Gasser, L., Gailly, N., Syta, E., & Ford, B. (2018). OmniLedger: A Secure, Scale-Out, Decentralized Ledger via Sharding. In 2018 IEEE Symposium on Security and Privacy (SP) (pp. 583–598).

  13. Yu, M., Sahraei, S., Li, S., Avestimehr, S., Kannan, S., & Viswanath, P. (2020). Ohie: Blockchain Scaling Made Simple. In IEEE Symposium on Security and Privacy (SP).

  14. Goldberg, S., Naor, M., Papadopoulos, D., & Reyzin, L. (2020). SPHINX: A Password Store that Perfectly Hides Passwords from Itself. In 2020 IEEE Symposium on Security and Privacy (SP) (pp. 1051–1069).

  15. Boneh, D., Bünz, B., & Fisch, B. (2019). Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains. In Annual International Cryptology Conference (pp. 561–586). Springer.

  16. Gabizon, A., Williamson, Z., & Ciobotaru, O. (2019). PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive Arguments of Knowledge. Cryptology ePrint Archive, Report 2019/953.

  17. Maller, M., Bowe, S., Kohlweiss, M., & Meiklejohn, S. (2019). Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updateable Structured Reference Strings. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security (pp. 2111–2128).

  18. Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2018). Scalable, Transparent, and Post-Quantum Secure Computational Integrity. Cryptology ePrint Archive, Report 2018/046.

  19. Chiesa, A., Hu, Y., Maller, M., Mishra, P., Vesely, N., & Ward, N. (2019). Marlin: Preprocessing zkSNARKs with Universal and Updatable SRS. Cryptology ePrint Archive, Report 2019/1047.

  20. Bünz, B., Bootle, J., Boneh, D., Poelstra, A., Wuille, P., & Maxwell, G. (2018). Bulletproofs: Short Proofs for Confidential Transactions and More. In 2018 IEEE Symposium on Security and Privacy (SP) (pp. 315–334).

  21. Wang, J., & Wang, H. (2020). Fractal: Post-Quantum and Transparent Recursive Proofs from Holography. Cryptology ePrint Archive, Report 2020/1280.

  22. Tomescu, A., Abraham, I., Buterin, V., Drake, J., Feist, D., & Khovratovich, D. (2020). Aggregatable Subvector Commitments for Stateless Cryptocurrencies. In Security and Cryptography for Networks (pp. 45–64). Springer.

3

@vbuterin

Are you going to acknowledge this? I think you should. I think it’s ethical.

4

ISO those enthusiastic about this and who looking to contribute, please contact me here. it’s already well on its way in production, but I could use some fellow intellectuals and innovative engineers to help with this.

Github

Overpass Network on X

Me on X

5

trust isn’t about visibility but about verifiable integrity…

accountability can be achieved through cryptographic proofs without exposing personal data…

privacy is a right not a privilege…

6

Bitcoin Bridge Using HTLCs, OP_RETURN, and Stealth Addresses

The Bitcoin bridge in Overpass enables seamless integration between Bitcoin’s Layer 1 (L1) and Overpass’s Layer 2 (L2) scaling solution, leveraging Hashed Time-Locked Contracts (HTLCs), OP_RETURN, and stealth addresses for privacy, flexibility, and instant transactions.

Overview of the Bridge

The Bitcoin bridge operates by locking Bitcoin on L1 using an HTLC, generating proof of this lock, and creating equivalent Overpass BTC tokens on L2. These tokens can be used in Overpass channels for private and instant transactions. The bridge also facilitates rebalancing and transparent withdrawal back to Bitcoin’s L1.

HTLC and OP_RETURN Mechanism

  1. HTLC Construction
    An HTLC is created to lock Bitcoin on L1 with the following structure:

    \text{HTLC} = \{ \text{Amount: } a, \text{Receiver: } R, \text{Hash: } H(x), \text{Timeout: } T \}
    • a: The amount of Bitcoin locked.
    • R: Recipient address for settlement.
    • H(x): Hash of the preimage x.
    • T: Timeout after which the funds can be reclaimed by the sender.

    The HTLC ensures that the recipient can claim the funds only if they provide the preimage x that satisfies H(x) before the timeout T.

  2. Embedding Overpass Instructions with OP_RETURN
    The OP_RETURN field is used to include Overpass-specific instructions:

    \text{OP\_RETURN} = \{\text{Stealth Address: } S, \text{Rebalancing Flags: } F, \text{Metadata: } M\}
    • S: Stealth address dynamically generated for the recipient.
    • F: Flags for rebalancing or routing liquidity.
    • M: Additional transaction metadata for interoperability.

Stealth Address Generation

Stealth addresses are used to maintain recipient privacy. A stealth address is dynamically created for each transaction using the following process:

  1. Sender and Recipient Keys

    • Sender public key: P_s
    • Recipient public key: P_r

  2. Stealth Address Computation

    S = H(k_s \cdot P_r) \cdot G
    • k_s: Ephemeral private key generated by the sender.
    • P_r: Static public key of the recipient.
    • H: Hash function.
    • G: Elliptic curve generator point.

    The recipient can derive S using their private key without revealing any linkage to their identity.

Channel Rebalancing

When liquidity in channels needs to be redistributed, the bridge facilitates rebalancing:

  1. Detect Low Liquidity in a Channel

    \text{Liquidity\_Available}(C) < \text{Threshold}
    • C: Channel being monitored.
    • Threshold: Minimum acceptable liquidity.

  2. Dynamic Routing
    Use intermediary HTLCs and stealth addresses to route funds dynamically, maintaining balance across channels.

End-to-End Flow

  1. Deposit BTC to Overpass

    • The user sends BTC to the HTLC contract with Overpass instructions in OP_RETURN.
    • The Overpass network mints Overpass BTC equivalent to the locked Bitcoin.

  2. Transactions on Overpass

    • Users perform private transactions using zk-SNARKs and Overpass BTC.

  3. Withdraw BTC from Overpass

    • The user burns Overpass BTC, generating proof for the HTLC contract.
    • The contract releases BTC to a stealth address on L1.

Mathematical Guarantees

  1. HTLC Security

    \text{Pr}[\text{Funds stolen}] \leq 2^{-\lambda}
    • \lambda: Security parameter (e.g., 128 bits).

  2. Privacy via Stealth Addresses

    \text{Pr}[\text{Linkability}] \leq 2^{-\lambda}

  3. Rebalancing and Instant Finality

    \text{Time}_{finality} = O(1), \quad \text{Cost}_{rebalancing} = O(\log n)
    • n: Number of active channels.

Advantages of the Bitcoin Bridge

  1. Privacy by Design

    • Stealth addresses ensure unlinkable transactions.

  2. Instant Finality

    • Overpass channels provide cryptographic proofs of transaction finality without waiting for Bitcoin L1 confirmations.

  3. Seamless Interoperability

    • The bridge integrates Bitcoin and Overpass with minimal overhead.

  4. Dynamic Rebalancing

    • Automatically redistributes liquidity to maintain optimal channel functionality.

A Fully Trustless Mechanism

The Overpass Bitcoin bridge is a purely trustless mechanism. Unlike systems that rely on additional committees, validators, or centralized intermediaries, Overpass introduces only a small number of automated smart contracts. These contracts operate entirely on cryptographic principles and are verified mathematically through zk-SNARKs.

The bridge maintains Bitcoin’s native security model while enhancing it with additional privacy and scalability via hash-based locking and zero-knowledge proofs. The use of HTLCs and zk-SNARKs ensures there are no new trust assumptions, and, in fact, the security is arguably tighter. Attack vectors are minimized due to the robust cryptographic guarantees of Overpass, making the system inherently resistant to tampering or fraud.

By combining Bitcoin’s native strengths with Overpass’s innovative design, the bridge achieves trustless, private, and instant transactions without introducing additional security risks.

7

Transparency via expanded protocols on top…

Verifiable privacy. Maintaining audibility, for selective disclosures…

• transparency, optional :white_check_mark:
• privacy by default :white_check_mark:

8

OVERPASS: HOW THE PIECES FIT TOGETHER

The Core Components:

  1. Zero-Knowledge Proofs (using Plonky2)
    The foundation that makes everything possible:
  • Proves state transitions are valid without revealing details
  • Uses Goldilocks field for fast arithmetic
  • Poseidon hash functions optimize for ZK operations
  1. Sparse Merkle Trees (SMTs)
    Tracks the state efficiently:
  • Each leaf represents a user’s channel state
  • State includes: balance, nonce, transaction history
  • Roots provide compact representation of entire state
  • Makes proofs of inclusion/exclusion efficient
  1. Unilateral Channels
    The breakthrough application:
  • Users can update state independently
  • No need for counterparty to be online
  • Each update generates its own validity proof

How They Work Together:

Let’s follow a transaction from Alice to Bob:

  1. Alice wants to send 5 tokens to Bob:

    • Gets her current state from SMT
    • Increments her nonce
    • Creates new state reflecting -5 tokens

  2. Plonky2 generates a proof that:

    • Proves Alice’s current balance exists in SMT
    • Shows nonce is valid (incremented)
    • Demonstrates new state is correctly computed
    • All using Goldilocks field math for speed

  3. The proof gets committed:

    • New state hashed with Poseidon
    • Hash inserted into SMT
    • SMT root updated
    • Proof validates entire operation

  4. Bob can immediately verify:

    • Checks proof using Plonky2
    • Verifies SMT inclusion
    • No need to track global state
    • Instant finality

The Magic:

  • Plonky2 makes proofs fast and small
  • SMTs make state management efficient
  • Unilateral updates remove coordination overhead
  • Everything locks together cryptographically

Security emerges from the combination:

  • Can’t forge proofs (Plonky2)
  • Can’t tamper with state (SMTs)
  • Can’t replay transactions (nonces)
  • Can’t need consensus (unilateral)

It’s like a self-proving puzzle where:

  • Each piece mathematically proves it fits
  • The whole structure proves its own validity
  • No external verification needed
  • Yet anyone can verify it’s correct

Let me explain why zero-knowledge proofs are essential for Overpass, and why the system wouldn’t work without them.

Think of a traditional payment channel system. When Alice wants to send money to Bob, she needs to prove two critical things: that she has enough money to send, and that she hasn’t already spent that money somewhere else. In traditional systems, this requires keeping track of the entire transaction history or having validators watch for double-spending.

Overpass solves this fundamental challenge through zero-knowledge proofs, specifically using Plonky2 with Goldilocks fields. Here’s why this is crucial:

Without zero-knowledge proofs, Alice would need to reveal her entire transaction history to prove she has enough money. This would mean:

  1. Everyone would see all her previous transactions
  2. The system would need to store and verify this complete history
  3. Bob would need to check this entire history to accept the payment

But with Plonky2 zero-knowledge proofs in Overpass, Alice can prove she has enough money without revealing anything about her previous transactions. The proof mathematically demonstrates:

  • Her current balance exists in the Sparse Merkle Tree
  • This balance is sufficient for the payment
  • The nonce is valid and hasn’t been used before
  • The new state after the payment is correctly calculated

The Goldilocks field arithmetic makes these proofs fast and efficient, while Poseidon hashes ensure the proofs can be generated quickly. This is why Plonky2 specifically is crucial - it makes these complex mathematical proofs practical for real-world use.

Most importantly, zero-knowledge proofs enable unilateral channels - channels where Alice can update the state without Bob being online. This wouldn’t be possible in a traditional system because:

  1. There would be no way to prove state validity without revealing the full history
  2. Bob would need to be online to verify and sign every update
  3. The system would need validators or watchtowers to prevent fraud

The combination of Plonky2 proofs with Sparse Merkle Trees creates a unique system where:

  • States can be updated unilaterally
  • Proofs are small and fast to verify
  • Security is mathematically guaranteed
  • No history or external validation is needed

What this means:

Let me explain what this means in practical, real-world terms that demonstrate why this is such a powerful system.

In traditional banking or payment systems, making a transaction involves several parties and many checks. Think of writing a check - the bank needs to verify your balance, ensure the check hasn’t been cashed before, and coordinate with other banks. This process is slow and requires everyone to be online and communicating.

Overpass transforms this entirely. Here’s what it means in practice:

Imagine Alice runs a business and needs to pay multiple suppliers throughout the day. With Overpass:

  1. Instant Payments Without Dependencies
  • Alice can send payments at 3 AM even if her suppliers are asleep
  • Each payment is mathematically guaranteed to be valid
  • No waiting for bank approval or supplier confirmation
  • No need for suppliers to do anything to receive funds
  1. Privacy With Proof
    When Alice pays supplier Bob:
  • Bob sees only the specific payment meant for him
  • Bob can’t see Alice’s other transactions or total balance
  • Yet Bob has mathematical certainty the payment is valid
  • No need for Alice to reveal her business’s financial details
  1. Guaranteed Security Without Overhead
  • No possibility of Alice accidentally double-spending
  • No risk of payments being reversed or disputed
  • No need for Bob to wait for confirmations
  • No expensive infrastructure needed to prevent fraud
  1. Real-World Scalability
    For a business doing thousands of transactions:
  • Each transaction is processed independently
  • No slowdown as transaction volume grows
  • Minimal storage needs (just the latest state)
  • No coordination needed between parties

Compare this to traditional systems:

  • Banks need to coordinate and verify every transaction
  • Payment networks need massive infrastructure
  • Everyone needs to maintain transaction histories
  • Scaling requires more servers, more coordination

Or to regular blockchain systems:

  • Everyone needs to validate everything
  • Transactions compete for block space
  • Costs increase with network usage
  • Finality takes time

This means Overpass could enable:

  • High-frequency trading without counterparty risk
  • Micropayments that are too small to be practical today
  • Cross-border payments without intermediary banks
  • Machine-to-machine payments at massive scale

The system provides the security of a blockchain with the speed of cash and the privacy of a personal ledger - something that hasn’t been possible before.

9

Not sure why Overpass is a paradigm shift for Bitcoin and all of web3⁉️ Check out this thread on Bitcoin talk!
:point_down:₿