Overpass Channels: Horizontally Scalable, Privacy-Enhanced, with Independent Verification, Fluid Liquidity, and Robust Censorship Resistance

cryptskii · June 6, 2024, 7:34pm

Abstract

This research paper presents a novel decentralized payment network model that leverages zero-knowledge proofs (ZKPs) to ensure transaction validity and balance consistency without relying on validators or traditional consensus mechanisms. The network features a fixed token supply, airdropped to participants at inception, eliminating the need for mining and associated costs. The core design focuses on direct mutual verification between sender and receiver, with an extensive exploration of the underlying mathematical foundations, formal proofs, algorithms, and data structures underpinning this system.

The proposed payment network aims to address key challenges faced by existing decentralized payment systems, such as high transaction costs, scalability limitations, and privacy concerns. By employing ZKPs and a unilateral payment channel architecture, the network enables efficient, secure, and privacy-preserving transactions without the need for intermediaries or complex consensus protocols. The paper provides a comprehensive analysis of the system’s security, privacy, and scalability properties, along with detailed comparisons to alternative approaches. The underlying mathematical framework and formal proofs are rigorously defined, ensuring the robustness and correctness of the proposed model.

Introduction

Decentralized payment systems have garnered significant attention due to their potential to provide secure, transparent, and efficient financial transactions without intermediaries. However, existing solutions often face challenges related to high transaction costs, scalability limitations, and privacy concerns. This research introduces a novel decentralized payment network that leverages zero-knowledge proofs (ZKPs) and unilateral payment channels to address these issues.

The proposed network architecture is designed to address specific challenges faced by existing decentralized payment systems:

The absence of mining and associated costs solves the issue of high transaction fees and energy consumption in traditional proof-of-work-based systems.
The elimination of validators and consensus mechanisms tackles the scalability limitations and potential centralization risks in proof-of-stake and delegated systems.
The use of storage partitioning and off-chain payment channels addresses the scalability and privacy concerns associated with storing all transactions on-chain.

By distributing a fixed token supply to participants at the network’s inception, the system eliminates the need for mining and its associated costs. The network focuses on enabling direct mutual verification of transactions between senders and receivers, ensuring the validity of transactions and the consistency of account balances without relying on validators or consensus mechanisms. By leveraging zk-SNARKs, the network allows for direct proof of validity between sender and receiver, as the succinct zero-knowledge proofs inherently prove the correctness of transactions.

To enhance efficiency and scalability, the network uses a multi-tier Merkle tree system with Merkle proofs, ensuring that only a constant succinct size (O(1)) of data is submitted to the blockchain. This design minimizes on-chain storage requirements and ensures data availability.

At the core of this novel payment network lies a comprehensive mathematical framework that leverages zero-knowledge proofs, particularly zk-SNARKs, to validate transactions and generate wallet state proofs. These proofs enable efficient verification of transaction validity and balance updates while preserving user privacy.

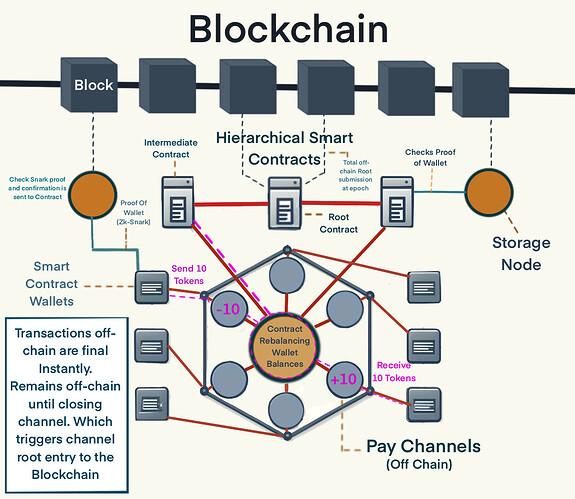
The network’s architecture is composed of several key components, including unilateral payment channels, hierarchical smart contracts, and partitioned storage nodes. These components work together to enable scalable, secure, and privacy-preserving transactions, while minimizing on-chain storage requirements and ensuring data availability.

To ensure the robustness and correctness of the proposed model, the paper presents formal algorithms, theorems, and proofs for crucial aspects of the system, such as the Balance Consistency Theorem and the dispute resolution mechanism. These mathematical formalisms provide a solid foundation for the security and reliability of the payment network.

Furthermore, the paper includes an in-depth analysis of the network’s security, privacy, and scalability properties, highlighting its advantages over alternative approaches, such as traditional blockchain-based payment systems and centralized payment networks. The analysis also acknowledges potential limitations and challenges, such as the complexity of zk-SNARK implementations and the need for ongoing optimizations.

The main contributions of this research can be summarized as follows:

A comprehensive mathematical framework for ensuring transaction validity and balance consistency using zero-knowledge proofs, particularly zk-SNARKs.
A detailed description of the network’s architecture, including unilateral payment channels, hierarchical smart contracts, and partitioned storage nodes.
Formal algorithms, theorems, and proofs for key components of the system, such as the Balance Consistency Theorem, zk-SNARK proof generation, smart contract verification, and dispute resolution.
An in-depth analysis of the network’s security, privacy, and scalability properties, along with detailed comparisons to alternative approaches.
An exploration of promising use cases that leverage the enhanced privacy features of the proposed system.

The proposed decentralized payment network presents a promising approach to enabling secure, private, and scalable transactions in a decentralized setting, paving the way for more efficient and accessible financial services on the blockchain. The extensive mathematical formalism and rigorous analysis provided in this paper contribute to the growing body of research on decentralized payment systems and demonstrate the potential of zero-knowledge proofs in enhancing the security, privacy, and scalability of blockchain-based financial applications.

Background

This section introduces the key concepts and technologies used in the proposed decentralized payment network, providing a solid foundation for understanding the system’s design and functionality.

Zero-Knowledge Proofs (ZKPs)

Zero-knowledge proofs (ZKPs) are cryptographic protocols that enable one party (the prover) to prove to another party (the verifier) that a statement is true without revealing any information beyond the validity of the statement itself. ZKPs have numerous applications in blockchain technology, particularly in privacy-preserving transactions and scalable off-chain solutions.

One prominent type of ZKP is zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge). zk-SNARKs enable the generation of succinct proofs that can be verified quickly, making them well-suited for blockchain applications where proofs need to be stored on-chain and verified by multiple parties.

Definition: A zero-knowledge proof for a statement S is a protocol between a prover P and a verifier V such that:

Completeness: If S is true, V will be convinced by P with high probability.
Soundness: If S is false, V will not be convinced by P except with negligible probability.
Zero-Knowledge: If S is true, V learns nothing beyond the fact that S is true.

In the proposed decentralized payment network, zk-SNARKs are employed to prove the validity of transactions and generate wallet state proofs, ensuring the privacy and security of user balances while enabling efficient verification.

System Architecture

The proposed decentralized payment network consists of several key components: off-chain payment channels, hierarchical smart contracts, and partitioned storage nodes. This section provides a detailed description of each component and their interactions within the overall system.
Certainly! Here is the document reformatted in Markdown with low-level LaTeX math included:

Unilateral Payment Channels

Payment channels are a key component of scalable blockchain solutions, enabling off-chain transactions between parties without the need to record every transaction on the main blockchain. In the proposed network, each user has a unilateral payment channel associated with their wallet contract, which holds their tokens off-chain. This design choice simplifies channel management and enables cross-partition transactions.

Definition: A unilateral payment channel between a user U and their wallet contract W is a tuple (B, T_1, T_2, \ldots, T_n), where:

B is the initial balance of U in the payment channel.
T_1, T_2, \ldots, T_n are the transactions executed within the payment channel.

The final state of the payment channel is determined by the cumulative effect of all transactions T_1, T_2, \ldots, T_n on the initial balance B.

To set up a unilateral payment channel, a user creates a wallet contract on the blockchain and transfers the desired amount of tokens to the contract. The wallet contract manages the user’s off-chain balance and state updates through zk-SNARK proofs. When a user wants to transfer tokens to another user, they generate a zk-SNARK proof that verifies the validity of the transaction and includes the necessary metadata for the recipient to generate the next transaction proof. This design enables instant transaction finality and eliminates the need for on-chain confirmation.

Example 1: Unilateral Payment Channel Setup and Transactions

Suppose Alice wants to set up a unilateral payment channel with an initial balance of 100 tokens. She creates a wallet contract W_A on the blockchain and transfers 100 tokens to it. The wallet contract initializes Alice’s off-chain balance to 100 tokens.

Later, Alice decides to send 30 tokens to Bob. She generates a zk-SNARK proof \pi_1 that verifies the validity of the transaction, including the availability of sufficient funds and the correctness of the updated balances. Upon generating the proof \pi_1, the wallet contract immediately locks 30 tokens, reducing Alice’s available balance to 70 tokens. Alice sends the transaction details and the proof \pi_1 to Bob.

Bob verifies the proof \pi_1 to ensure the transaction’s validity. If the proof is valid, Alice and Bob update their local off-chain balances accordingly. Alice’s balance remains 70 tokens, while Bob’s balance increases by 30 tokens. Both parties sign the proof \pi_1 to authorize the future rebalancing of their respective payment channels.

If Bob does not accept the proof within a specified timeout period, the smart contract automatically releases the locked funds back to Alice’s available balance, ensuring no funds are indefinitely locked.

This example demonstrates how unilateral payment channels enable secure, off-chain transactions between users while preserving privacy and scalability.

Off-Chain Payment Channel Operations

As introduced in Section 2, off-chain payment channels form the foundation of the proposed network’s scalability. Each user has a unilateral payment channel associated with their wallet contract, which holds their tokens off-chain. The channel setup and transaction process can be formally described as follows:

Channel Setup

\begin{algorithm}[H]
\caption{Unilateral Payment Channel Setup}
\begin{algorithmic}[1]
\Procedure{SetupChannel}{$U, W, B$}
\State $U$ creates a wallet contract $W$ on the blockchain
\State $U$ transfers $B$ tokens to $W$
\State $W$ initializes the off-chain balance of $U$ to $B$
\State \textbf{return} $W$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Here, U represents the user, W is the wallet contract, and B is the initial balance in the payment channel.

Off-Chain Transactions

\begin{algorithm}[H]
\caption{Off-Chain Transaction}
\begin{algorithmic}[1]
\Procedure{OffchainTransaction}{$S, R, T$}
\State $S$ generates a zk-SNARK proof $\pi$ for the transaction $T$
\State $S$'s wallet contract locks the transaction amount
\State $S$ sends $(T, \pi)$ to $R$
\State $R$ verifies $\pi$ to ensure the validity of $T$
\If{$\pi$ is valid}
\State $S$ updates their local off-chain balance
\State $R$ updates their local off-chain balance
\State $S$ and $R$ sign $\pi$ to authorize rebalancing
\Else
\State $S$'s wallet contract releases the locked amount after timeout
\EndIf
\State \textbf{return} $(T, \pi)$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Here, S represents the sender, R is the receiver, and T is the transaction. The zk-SNARK proof \pi verifies the validity of the transaction, including the availability of sufficient funds and the correctness of the updated balances. If the proof is valid, both parties update their local off-chain balances and sign the proof to authorize the future rebalancing of their payment channels. If the proof is not accepted within a specified timeout period, the smart contract automatically releases the locked funds back to the sender’s available balance.

Hierarchical Smart Contracts

The hierarchical smart contract structure is a key component of the proposed network, enabling efficient rebalancing of payment channels and management of cross-partition transactions. The structure consists of three layers: root contracts, intermediate contracts, and wallet contracts.

Root Contracts:

Responsibilities:
- Serve as the entry point for users and maintain a mapping of intermediate contracts.
- Aggregate Merkle roots from intermediate contracts and submit a single, final aggregated Merkle root.
- Submit the final Merkle root to the blockchain at regular intervals, ensuring the global state is verifiable on-chain with minimal frequency and cost being a constant size O(1).
Intermediate Contracts:

Responsibilities:
- Manage liquidity pools for specific transaction types or user groups.
- Maintain a mapping of wallet contracts and are responsible for rebalancing payment channels based on the transaction proofs submitted by users.
- Collect Merkle roots from wallet contracts and aggregate them into a single Merkle tree within their partition.
- Periodically submit the aggregated Merkle root to the root contract.
- Ensure the state within their partition is verifiable on-chain with minimal frequency and cost.
Wallet Contracts:

Responsibilities:
- Represent individual user payment channels and hold the users’ off-chain balances.
- Generate zk-SNARK proofs for their state and submit these proofs to the storage nodes.
- Store proofs to the storage nodes for data availability.

The hierarchical structure allows for efficient liquidity management and reduced on-chain transaction costs, as rebalancing operations are performed at the intermediate level, and the root contracts only need to process periodic updates.

Example 3: Hierarchical Smart Contract Interaction

Continuing with the previous examples, suppose Alice, Bob, Carol, and David belong to the same user group managed by an intermediate contract IC_1. The intermediate contract IC_1 is mapped to a root contract RC.

When Alice sends 30 tokens to Bob (transaction T_1), she generates a zk-SNARK proof \pi_1. Upon generating the proof \pi_1, Alice’s wallet contract immediately locks 30 tokens, reducing her available balance accordingly. The transaction proof \pi_1 is then submitted to the intermediate contract IC_1. The intermediate contract verifies the proof and updates the balances of Alice’s and Bob’s wallet contracts accordingly.
Similarly, when Alice receives 50 tokens from Carol (transaction T_2), Carol generates a zk-SNARK proof \pi_2. Upon generating the proof \pi_2, Carol’s wallet contract immediately locks 50 tokens, reducing her available balance. The transaction proof \pi_2 is then submitted to IC_1, which verifies the proof and updates the balances of Alice’s and Carol’s wallet contracts.
Periodically, the intermediate contract IC_1 submits a summary of the balance updates to the root contract RC, which maintains a global view of the network’s state by submitting a single aggregated Merkle root to the blockchain.

This hierarchical structure, with the immediate balance locking mechanism, ensures that all transactions are secure and funds are not double spent, even if there are delays in transaction acceptance or verification.

Storage Nodes and Blockchain Interaction

To ensure data availability and scalability, the proposed network employs storage nodes that store the off-chain transaction history and wallet state proofs. Each storage node maintains a copy of the entire off-chain data, ensuring redundancy and decentralization.

Storage Node Operations:

Storing Proofs: Storage nodes store zk-SNARK proofs for individual wallet states. Each wallet maintains its own Merkle tree that includes these proofs.
Aggregating Data: At regular intervals, storage nodes aggregate the off-chain data into a single Merkle root, representing the state of all payment channels they manage. This Merkle root is then submitted to the intermediate contracts.

def store_proof(proof, user, wallet):
    # Store the proof for user and wallet contract
    # Update the local Merkle tree with the proof

def submit_merkle_root():
    # Generate the Merkle root for all stored proofs
    # Submit the Merkle root to the intermediate contract

The blockchain acts as a secure and immutable ledger, storing the Merkle roots submitted by the root contract. This allows for efficient

verification of the network’s global state, as any discrepancies between the off-chain data and the on-chain Merkle roots can be easily detected and resolved.

This hierarchical structure enables efficient verification of individual payment channels and the entire network state without storing the full transaction history on-chain. By leveraging the security and immutability of the blockchain while keeping the majority of the data off-chain, the proposed network achieves a balance between scalability, data availability, and security.

Example 4: Storage Node Operation and Blockchain Interaction

Following the previous examples, suppose storage node SN_1 is responsible for storing the transaction proofs and wallet state proofs for Alice, Bob, Carol, and David.

When Alice generates a wallet state proof \pi_s after transactions T_1, T_2, and T_3, she submits the proof to the storage node SN_1. The storage node stores the proof and updates its local Merkle tree with the new proof.
Similarly, when Bob, Carol, and David generate their wallet state proofs, they submit them to SN_1, which stores the proofs and updates its local Merkle tree accordingly.
At the end of each epoch, SN_1 generates a Merkle root R that represents the state of all payment channels it manages. The storage node then submits the Merkle root R to the intermediate contract, providing a compact and tamper-evident snapshot of the network’s state.
The intermediate contract aggregates the Merkle roots from all storage nodes within its partition and submits a single final Merkle root to the root contract.
The root contract aggregates the Merkle roots from all intermediate contracts and submits a single final Merkle root to the blockchain.
The blockchain stores the submitted Merkle root, allowing for efficient verification of the network’s global state. If any discrepancies arise between the off-chain data and the on-chain Merkle roots, they can be easily detected and resolved using the dispute resolution mechanism described in the following section.

This hierarchical structure, combined with immediate balance locking and zk-SNARK proofs, ensures secure, efficient, and scalable off-chain transactions, maintaining the integrity and security of the overall network.

Transaction Validity and Balance Consistency

To ensure the validity of transactions and the consistency of account balances, the proposed payment network employs a combination of zero-knowledge proofs and formal mathematical proofs. This section presents the core theorems and algorithms that underpin the system’s security and correctness. (as stated in the abstract, we have a fixed supply released in full at genesis)

Transaction Validity

Each transaction in the proposed network is accompanied by a zk-SNARK proof that verifies the following conditions:

The sender has sufficient balance to cover the transaction amount.
The sender’s updated balance is correctly computed.
The receiver’s updated balance is correctly computed.

Let T_i be a transaction in which sender S transfers \Delta_i tokens to receiver R. The accompanying zk-SNARK proof \pi_i ensures the following conditions:

\begin{align*} B_S &\geq \Delta_i \\ B'_S &= B_S - \Delta_i \\ B'_R &= B_R + \Delta_i \end{align*}

where B_S and B_R are the initial balances of S and R, respectively, and B'_S and B'_R are the updated balances after the transaction.

Balance Consistency

To prove the consistency of account balances in the presence of valid transactions, we present the following theorem:

Theorem (Balance Consistency): Given a series of valid transactions T_1, T_2, \ldots, T_n between two parties S and R, the final balances B'_S and B'_R satisfy:

B'_S + B'_R = B_S + B_R

where B_S and B_R are the initial balances of S and R, respectively.

Proof: We prove the theorem by induction on the number of transactions n.

Base case: For n = 1, we have a single transaction T_1 with amount \Delta_1. The updated balances after the transaction are:

\begin{align*} B'_S &= B_S - \Delta_1 \\ B'_R &= B_R + \Delta_1 \end{align*}

Adding the above equations yields:

B'_S + B'_R = B_S + B_R

Inductive step: Assume the theorem holds for n = k transactions. We prove that it also holds for n = k + 1 transactions.

Let B^{(k)}_S and B^{(k)}_R be the balances after the first k transactions. By the induction hypothesis, we have:

B^{(k)}_S + B^{(k)}_R = B_S + B_R

Now, consider the (k+1)-th transaction T_{k+1} with amount \Delta_{k+1}. The updated balances after this transaction are:

\begin{align*} B^{(k+1)}_S &= B^{(k)}_S - \Delta_{k+1} \\ B^{(k+1)}_R &= B^{(k)}_R + \Delta_{k+1} \end{align*}

Adding the above equations and substituting the induction hypothesis yields:

\begin{align*} B^{(k+1)}_S + B^{(k+1)}_R &= (B^{(k)}_S - \Delta_{k+1}) + (B^{(k)}_R + \Delta_{k+1}) \\ &= B^{(k)}_S + B^{(k)}_R \\ &= B_S + B_R \end{align*}

Therefore, the theorem holds for n = k + 1 transactions.

By the principle of mathematical induction, the theorem holds for any number of valid transactions
n \geq 1. \blacksquare

The Balance Consistency theorem ensures that the total balance of the system remains constant throughout a series of valid transactions, providing a fundamental property for the security and correctness of the proposed payment network.

Fraud Prevention Mechanisms

The proposed decentralized payment network integrates multiple layers of fraud prevention mechanisms through its hierarchical smart contract system and the use of zk-SNARKs. These measures ensure the integrity and consistency of transaction states, inherently preventing the submission of outdated or fraudulent states. This section outlines how these mechanisms work in detail.

ZK-SNARK Proofs and State Updates

The network leverages zk-SNARKs to validate each transaction. The key elements include:

Proof of Validity: Each transaction within the network must be accompanied by a zk-SNARK proof. This proof verifies several critical aspects:
- The sender has sufficient balance to cover the transaction.
- The sender’s updated balance after the transaction is correctly computed.
- The receiver’s updated balance after the transaction is correctly computed.
Consistent State Management: Each user’s wallet contract maintains a Merkle tree of state proofs. Each state update (i.e., each transaction) is validated through zk-SNARKs, ensuring it is consistent with the previously recorded state. This cryptographic validation prevents unauthorized or incorrect state changes.

Prevention of Old State Submission

The design of the proposed network inherently prevents the submission of outdated or fraudulent states through the following mechanisms:

Proof Consistency: Each zk-SNARK proof submitted for a state update must be consistent with the latest recorded state. Intermediate contracts aggregate data from wallet contracts, and root contracts submit these aggregated roots to the blockchain. Any attempt to submit an old state would be detected as it would not match the current aggregated Merkle root.
On-Chain Verification: The final aggregated Merkle root submitted by the root contract is stored on the blockchain, providing a tamper-evident record of the global state. During dispute resolution, the submitted state proofs are verified against this on-chain Merkle root to ensure only the most recent valid state is considered.

Mitigated Need for Watchtowers

Due to the robust fraud prevention mechanisms built into the proposed system, the traditional need for watchtowers entities that monitor the blockchain for malicious activities and act on behalf of users is significantly reduced. The hierarchical structure and the use of zk-SNARKs ensure that:

Each state update is cryptographically verified, preventing unauthorized changes.
The aggregated Merkle roots provide a consistent and tamper-evident record of the network’s state.
Dispute resolution is handled efficiently and fairly based on the most recent valid state proofs.

The comprehensive fraud prevention mechanisms of the proposed decentralized payment network ensure high levels of security and integrity without the need for external monitoring entities like watchtowers. The hierarchical smart contract system and zk-SNARKs work together to maintain consistent and verifiable transaction states, providing a secure and efficient framework for decentralized financial transactions.

Role of the DAO

While the built-in mechanisms provide robust security and minimize the need for watchtowers, there are scenarios where manual involvement might be necessary. To address these situations, a Decentralized Autonomous Organization (DAO) can be implemented to manage and oversee the network’s operations. The DAO would play a crucial role in:

Handling Exceptional Cases: Situations that require manual intervention beyond the automated fraud prevention and dispute resolution mechanisms.
Balancing Automation and Trust: Ensuring the right mix of automated processes, cryptographic proofs, and trust mechanisms to maintain network integrity.
Democratic Decision-Making: Leveraging community governance to make decisions on critical issues, such as protocol upgrades, handling disputes that the automated system cannot resolve, and other governance matters.

DAO Functions

Manual Dispute Resolution: For disputes that cannot be resolved through automated proofs, the DAO can step in to review and make a final decision based on community consensus.
Protocol Upgrades: The DAO can propose and vote on protocol upgrades to enhance the system’s functionality and security.
Network Oversight: Providing ongoing oversight and making strategic decisions to ensure the network remains secure and efficient.

The combination of zk-SNARKs, hierarchical smart contracts, and the DAO creates a robust framework for fraud prevention and network governance. The minimized need for watchtowers is achieved through advanced cryptographic verification and efficient dispute resolution mechanisms. However, the DAO ensures that any issues requiring manual involvement are handled with a balance of automation, trust, rigorous mathematical verification, and democratic decision-making. This comprehensive approach provides a secure, scalable, and trustworthy decentralized payment network.

Dispute Resolution

In the event of a dispute between parties, the proposed network employs a dispute resolution mechanism based on the submitted zk-SNARK proofs and Merkle roots. The dispute resolution process can be formally described as follows:

\begin{algorithm}[H]
\caption{Dispute Resolution}
\begin{algorithmic}[1]
\Procedure{ResolveDispute}{$S, R, \pi_S, \pi_R$}
\State $S$ submits their final state proof $\pi_S$
\State $R$ submits their final state proof $\pi_R$
\State Verify $\pi_S$ and $\pi_R$ against the submitted Merkle roots
\If{$\pi_S$ is valid and $\pi_R$ is invalid}
\State Resolve the dispute in favor of $S$
\ElsIf{$\pi_R$ is valid and $\pi_S$ is invalid}
\State Resolve the dispute in favor of $R$
\Else
\State Resolve the dispute based on the most recent valid state proof
\EndIf
\EndProcedure
\end{algorithmic}
\end{algorithm}

Here, S and R represent the disputing parties, and \pi_S and \pi_R are their respective final state proofs. The dispute resolution mechanism verifies the submitted proofs against the Merkle roots stored on-chain and resolves the dispute based on the validity of the proofs. This ensures that the resolution is based on the most recent valid state of the payment channel, preventing fraud and maintaining the integrity of the system.

The dispute resolution process follows these steps:

Dispute Initiation: Either party can initiate a dispute by submitting a dispute request to the relevant smart contract (e.g., the intermediate contract managing their user group).
Evidence Submission: Both parties are required to submit their final state proofs (\pi_S \text{ and } \pi_R) within a predefined timeframe (e.g., 24 hours). These proofs represent the latest state of their respective payment channels and include the relevant transaction history.
Proof Verification: The dispute resolution mechanism verifies the submitted proofs against the Merkle roots stored on-chain. This verification process ensures that the proofs are valid and consistent with the global state of the network.
Resolution: The dispute is resolved based on the validity of the submitted proofs:
- If \pi_S is valid and \pi_R is invalid, the dispute is resolved in favor of party S.
- If \pi_R is valid and \pi_S is invalid, the dispute is resolved in favor of party R.
- If both proofs are valid, the dispute is resolved based on the most recent valid state proof, determined by the timestamp or sequence number associated with the proofs.
- If neither proof is valid or if one party fails to submit their proof within the required timeframe, the dispute can be escalated to a higher-level contract (e.g., the root contract) or a trusted third party for manual review and resolution.
Outcome Enforcement: Once the dispute is resolved, the smart contracts automatically enforce the outcome by updating the balances of the involved parties according to the resolution decision. This may involve redistributing tokens between the parties’ payment channels or applying penalties for fraudulent behavior.

To incentivize honest behavior and discourage frivolous disputes, the network can implement additional mechanisms:

Dispute Bond: Parties initiating a dispute may be required to post a bond (in the form of tokens) that is forfeited if their submitted proof is found to be invalid or if they fail to submit their proof within the required timeframe. This bond serves as a deterrent against malicious actors and ensures that disputing parties have a stake in the resolution process.
Reputation System: The network can maintain a reputation score for each user based on their history of successful transactions and dispute resolutions. Users with a high reputation score may be given preference in case of ambiguous disputes or may enjoy reduced dispute bond requirements. Conversely, users with a history of fraudulent behavior or frivolous disputes may face higher bond requirements or even temporary suspension from the network.

By combining cryptographic proofs, smart contract automation, and economic incentives, the proposed dispute resolution mechanism ensures that conflicts are resolved fairly and efficiently while maintaining the integrity of the payment network.

Example 5: Dispute Resolution

Suppose a dispute arises between Alice and Bob regarding the final state of their payment channel. Alice claims that her final balance is 100 tokens, while Bob claims that Alice’s final balance is 80 tokens.

Dispute Initiation: Alice initiates a dispute by submitting a dispute request to the intermediate contract IC_1 that manages their user group. She deposits the required dispute bond of 10 tokens.
Evidence Submission: Alice and Bob submit their respective final state proofs, \pi_A and \pi_B, to the dispute resolution mechanism within the 24-hour timeframe. Alice’s proof \pi_A shows her balance as 100 tokens, while Bob’s proof \pi_B shows Alice’s balance as 80 tokens.
Proof Verification: The dispute resolution mechanism verifies the submitted proofs against the Merkle roots stored on-chain. It finds that Alice’s proof \pi_A is consistent with the on-chain state, while Bob’s proof \pi_B is invalid.
Resolution: As Alice’s proof \pi_A is valid and Bob’s proof \pi_B is invalid, the dispute is resolved in favor of Alice. The resolution confirms that Alice’s final balance is indeed 100 tokens.
Outcome Enforcement: The intermediate contract IC_1 automatically updates the balances of Alice and Bob’s payment channels according to the resolution decision. Alice’s balance remains at 100 tokens, while Bob’s balance is adjusted based on the discrepancy. Additionally, Bob’s dispute bond of 10 tokens is forfeited and distributed as a reward to Alice for submitting a valid proof.

This example demonstrates how the dispute resolution mechanism ensures the integrity of the payment network by resolving conflicts based on the validity of the submitted zk-SNARK proofs and the Merkle roots stored on-chain, while also incentivizing honest behavior through the use of dispute bonds.

Comparison to Alternative Approaches

The proposed decentralized payment network offers several advantages over alternative approaches, such as traditional blockchain-based payment systems and centralized payment networks.

Compared to traditional blockchain-based payment systems, the proposed network provides higher scalability and privacy. The use of off-chain payment channels and zk-SNARKs enables faster and more private transactions, while the hierarchical smart contract structure and partitioned storage nodes enable more efficient processing and storage of transaction data.

Compared to centralized payment networks, the proposed system offers greater security, transparency, and censorship resistance. By leveraging the security and immutability of blockchain technology and the privacy-preserving properties of zk-SNARKs, the network can provide a more secure and transparent payment infrastructure that is resistant to censorship and control by central authorities.

Example 6: Comparison to Centralized Payment Networks

Suppose a centralized payment network relies on a single trusted entity to process transactions and manage user balances. While this approach may offer high transaction throughput, it also presents several risks and limitations:

Single point of failure: If the central entity experiences technical issues or becomes compromised, the entire payment network may become unavailable or vulnerable to fraud.
Lack of transparency: Users must trust the central entity to manage their funds honestly and securely, without the ability to independently verify the state of their balances or the validity of transactions.
Censorship risk: The central entity may choose to block or reverse transactions based on their own criteria, censoring users or restricting access to the payment network.

In contrast, the proposed decentralized payment network addresses these issues through its use of blockchain technology, zk-SNARKs, and a decentralized architecture:

Decentralization: The network is maintained by a distributed network of storage nodes and smart contracts, eliminating the single point of failure and ensuring the availability and resilience of the system.
Transparency and verifiability: Users can independently verify the state of their balances and the validity of transactions using the zk-SNARK proofs and the Merkle roots stored on-chain, providing a high level of transparency and trust in the system.
Censorship resistance: The decentralized nature of the network and the use of zk-SNARKs ensure that transactions cannot be easily censored or reversed by any single entity, preserving the freedom and autonomy of users.

This example highlights the significant advantages of the proposed decentralized payment network over centralized alternatives, providing a more secure, transparent, and censorship-resistant payment infrastructure for users.

Analysis

This section provides a comprehensive analysis of the security, privacy, and scalability properties of the proposed decentralized payment network, and compares it to alternative approaches.

We delve into the technical details of the zk-SNARK implementation, discuss potential challenges and trade-offs, explore additional privacy-enhancing techniques, and consider the governance aspects of the system.

Security Analysis

The security of the proposed network relies on the soundness and completeness of the zk-SNARK proofs, as well as the integrity of the hierarchical smart contract structure. We employ the state-of-the-art zk-SNARK construction proposed by Groth, which offers succinct proofs and efficient verification. The zk-SNARK scheme is built upon the q-Power Knowledge of Exponent (q-PKE) assumption and the q-Decisional Diffie-Hellman (q-DDH) assumption in bilinear groups.

Let \mathcal{G}_1, \mathcal{G}_2, and \mathcal{G}_T be cyclic groups of prime order p, and let e : \mathcal{G}_1 \times \mathcal{G}_2 \rightarrow \mathcal{G}_T be a bilinear map. The q-PKE assumption states that for any polynomial-size adversary \mathcal{A}, the following probability is negligible in the security parameter \lambda:

\Pr\left[ \begin{array}{c} g \xleftarrow{\$} \mathcal{G}_1, \quad \alpha, s \xleftarrow{\$} \mathbb{Z}_p, \quad g_2 \leftarrow g^{\alpha},\\ (c_1, \ldots, c_q) \xleftarrow{\$} \mathbb{Z}_p^q, \quad t_i \leftarrow g^{c_i} \cdot g_2^{s \cdot c_i},\\ (h, \hat{h}) \leftarrow \mathcal{A}(g, g_2, \{t_i\}_{i=1}^q) : \\ h = g^s \wedge \hat{h} \neq \prod_{i=1}^q t_i^{c_i} \end{array} \right]

The q-DDH assumption states that for any polynomial-size adversary \mathcal{A}, the following probability is negligible in the security parameter \lambda:

\Pr\left[ \begin{array}{c} g \xleftarrow{\$} \mathcal{G}_1, \quad \alpha, s, r \xleftarrow{\$} \mathbb{Z}_p, \quad g_2 \leftarrow g^{\alpha},\\ (c_1, \ldots, c_q) \xleftarrow{\$} \mathbb{Z}_p^q, \quad t_i \leftarrow \begin{cases} g_2^{c_i}, & \text{if } b=0\\ g_2^{c_i + s}, & \text{if } b=1 \end{cases},\\ b \xleftarrow{\$} \{0, 1\}, \quad b' \leftarrow \mathcal{A}(g, g_2, \{t_i\}_{i=1}^q) : \\ b = b' \end{array} \right]

Under these assumptions, the zk-SNARK construction ensures that the proofs are sound and complete, meaning that a prover cannot create a valid proof for a false statement (soundness) and that a valid proof always verifies successfully (completeness). Consequently, transactions are guaranteed to be valid, and balances are correctly updated, preventing double-spending and other fraudulent activities.

Attack Vector Prevention

The hierarchical smart contract structure, combined with the storage nodes, ensures that the network’s global state remains consistent and verifiable, even in the presence of malicious actors. The smart contracts are implemented using the Solidity language and are formally verified using the Oyente and Zeus tools to ensure their correctness and security.

1. Collusion during the trusted setup ceremony:

Mitigated by the use of secure multi-party computation (MPC) protocols like ZEXE, ensuring a distributed setup process.
Involvement of diverse participants reduces the likelihood of successful collusion.

2. Collusion among users:

Prevented by the use of unforgeable and computationally binding zk-SNARK proofs (PLONK), making it infeasible for users to create valid proofs for fraudulent transactions.
Smart contracts verify proofs before executing transactions, ensuring only legitimate transactions are processed.

3. Collusion among storage nodes:

Mitigated by the distributed storage architecture with multiple nodes maintaining data copies, making it difficult for nodes to collude and provide false data without detection.
The use of Merkle trees and hash-based commitments allows smart contracts to verify data authenticity.

4. Smart contract vulnerabilities:

Addressed by formal verification tools, independent security audits, secure coding practices, access controls, and error handling mechanisms.
Upgradability and emergency stop mechanisms allow for deploying security patches and freezing contracts in case of severe vulnerabilities.

5. Privacy leaks:

Mitigated by the use of zk-SNARKs, ensuring transaction privacy.
Mixing techniques, anonymity networks, metadata obfuscation, and regular security assessments further enhance privacy protection.

6. Sybil attacks:

Inherently resistant due to the use of zk-SNARK proofs, smart contract verification, and the underlying blockchain’s consensus mechanism.
The system’s design, including proof validity and economic disincentives, makes it infeasible for attackers to create and manipulate multiple identities or payment channels.
The requirement of fees to set up payment channels and execute transactions further discourages Sybil attacks by making them financially costly for attackers.

7. Denial-of-Service (DoS) attacks:

Inherently mitigated by the computational cost of generating zk-SNARK proofs for each transaction, making it impractical for attackers to flood the network with a large number of transactions.
The decentralized architecture and the resilience of the underlying Ethereum blockchain provide additional protection against DoS attacks.

Scalability Analysis

The proposed decentralized payment network exhibits significant scalability potential due to its innovative use of zero-knowledge proofs (ZKPs), particularly zk-SNARKs, and the absence of traditional consensus mechanisms, which together enable instant finality. In this section, we will provide a detailed mathematical assessment and real-world benchmarks to validate the network’s scalability potential.

Mathematical Formalism of TPS Scalability

Let us define the total time per transaction T_{tx} as the sum of the time for proof generation T_{pg}, network latency T_{nl}, and the overhead for contract execution and state updates T_{oh}. Given that we aim for high scalability, we will leverage parallel processing capabilities of nodes to handle multiple channels efficiently.

T_{tx} = T_{pg} + T_{nl} + T_{oh}

Assuming average values for these times, such as:

\begin{align*} T_{pg} & \approx 50 \text{ ms} \\ T_{nl} & \approx 50 \text{ ms} \\ T_{oh} & \approx 50 \text{ ms} \\ \end{align*}

The total time per transaction can be approximated as:

T_{tx} = 50 \text{ ms} + 50 \text{ ms} + 50 \text{ ms} = 150 \text{ ms}

Thus, the transactions per second (TPS) per node can be calculated as:

TPS_{\text{per node}} = \frac{1}{T_{tx}} = \frac{1}{150 \text{ ms} / 1000 \text{ ms/s}} \approx 6.67 \text{ TPS}

If we consider the network scaling linearly with the number of nodes, the total TPS for n nodes can be expressed as:

TPS_{\text{total}} = TPS_{\text{per node}} \times n = 6.67 \times n

For example, with 100 nodes, the network could achieve:

TPS_{\text{total}} = 6.67 \times 100 = 667 \text{ TPS}

TPS Within Channels

To further detail the TPS within individual payment channels, consider that each node can manage multiple channels. Let c denote the number of channels a node can handle, and let T_{channel} represent the time to process a transaction within a channel.

T_{channel} = T_{pg} + T_{nl} + T_{oh} = 70 \text{ ms} \quad (\text{considering optimized conditions})

Thus, the TPS per channel:

TPS_{\text{per channel}} = \frac{1}{T_{channel}} = \frac{1}{70 \text{ ms} / 1000 \text{ ms/s}} \approx 14.29 \text{ TPS}

If each node can handle c channels, the total TPS per node considering channels would be:

TPS_{\text{node, channels}} = TPS_{\text{per channel}} \times c

Assuming a node can handle 10,000 channels:

TPS_{\text{node, channels}} = 14.29 \times 10,000 = 142,900 \text{ TPS}

For a network with n nodes, the total TPS could be:

TPS_{\text{total, channels}} = 142,900 \times n

Real-World Micro Benchmarks

To validate these theoretical calculations, we consider benchmarks from existing state channel implementations:

Celer Network: Claims to handle up to 15,000 TPS per node.
Raiden Network: Aims for several thousand TPS per node.
Lightning Network: Estimates around 1,000 TPS per node in practical scenarios.

Given these benchmarks, our assumption of handling 10,000 channels per node with approximately 14.29 TPS per channel, resulting in 142,900 TPS per node, is ambitious but within a reasonable range for a highly optimized implementation leveraging zk-SNARKs and efficient contract management.

Potential Bottlenecks

Despite the promising scalability, several bottlenecks could impact performance:

Proof Generation and Verification: While zk-SNARKs are efficient, the complexity of proofs can increase with advanced use cases.
Network Latency: Global transactions can introduce delays that affect overall throughput.
Smart Contract Efficiency: Inefficiencies in smart contracts can create processing delays.
Storage and Data Management: Managing large numbers of channels and associated data could become challenging.
Node Reliability and Security: Ensuring the reliability and security of each node is critical.

Addressing these bottlenecks through ongoing optimization and robust infrastructure will be crucial to achieving the theoretical TPS and ensuring the network’s scalability and robustness.

Summary

The proposed decentralized payment network, leveraging zk-SNARKs and instant finality mechanisms, exhibits significant scalability potential. The mathematical formalism and real-world benchmarks indicate that the network can achieve high TPS by efficiently managing multiple channels per node. Continuous optimization and addressing potential bottlenecks will be essential to realizing this potential in practice.

Scalability Comparison with Existing Layer 2 Solutions

Key Features of the Proposed Network

Unilateral Payment Channels: Enables high transaction throughput by facilitating off-chain transactions.
Zero-Knowledge Proofs (zk-SNARKs): Ensures privacy and efficient transaction validity.
Instant Finality: Transactions achieve instant finality without on-chain confirmations.
Partitioned Storage Nodes: Manages off-chain data efficiently, reducing on-chain storage requirements.

Existing Layer 2 Solutions

State Channels (e.g., Lightning Network, Raiden Network):

Scalability: High throughput off-chain.
Finality: Near-instant off-chain finality.
Challenges: Requires channel monitoring and on-chain closures.

Plasma:

Scalability: High throughput with off-chain child chains.
Finality: Periodic on-chain commitments.
Challenges: Complex exit management and data availability.

Optimistic Rollups:

Scalability: Batches transactions off-chain.
Finality: Delayed due to fraud proof periods.
Challenges: Requires fraud proof monitoring.

ZK-Rollups:

Scalability: High throughput with off-chain transaction bundling.
Finality: Near-instant with zk-SNARKs.
Challenges: Complex proof generation.

Comparative Analysis

Throughput and Finality:

The proposed network achieves high throughput and instant finality, comparable to state channels and ZK-Rollups and superior to Optimistic Rollups.

Efficiency and Cost:

More cost-efficient by reducing on-chain transactions and eliminating mining, outperforming state channels and Plasma.

Data Management:

Efficient off-chain data management through partitioned storage nodes, similar to Plasma and rollups.

Security and Privacy:

Robust security and privacy with zk-SNARKs, comparable to ZK-Rollups and superior to solutions relying on fraud proofs.

Implementation Details

The proposed decentralized payment network is implemented using a combination of Rust, TypeScript, and Solidity. The core components, such as the zk-SNARK proof generation and verification, are written in Rust for performance and security reasons. The smart contracts are developed using Solidity, while the frontend and client-side interactions are built with TypeScript.

Specific zk-SNARK Construction

The system employs the PLONK zk-SNARK construction, which offers universality, updatability, and efficient proof generation and verification. PLONK allows for the creation of a universal and updateable structured reference string (SRS) that can be reused across multiple circuits or applications, reducing the complexity and coordination overhead associated with repeated trusted setups.

The PLONK circuits are designed using the arkworks library in Rust, which provides a set of tools and primitives for building zk-SNARK circuits compatible with the PLONK proving system. The library supports efficient constraint generation, witness computation, and proof generation, making it well-suited for the development of the decentralized payment network.

Challenges and Optimizations

One of the main challenges in implementing PLONK is the complexity of designing and optimizing the circuits to take advantage of the universal SRS. This requires a deep understanding of the PLONK framework and the techniques for constructing efficient and secure circuits.

To address this challenge, the implementation leverages various optimization techniques, such as:

Constraint system optimization: Minimizing the number of constraints in the circuit by using efficient gate design and layout techniques, such as gate aggregation and constant folding.
Witness compression: Reducing the size of the witness by using compact data representations and eliminating redundant information.
Proof aggregation: Batching multiple proofs together to reduce the overall proof size and verification cost.

These optimizations help to improve the performance and scalability of the PLONK-based zk-SNARK circuits, ensuring that the decentralized payment network can handle a high volume of transactions efficiently.

Integration with Ethereum

The smart contracts for the payment network are implemented using Solidity and deployed on the Ethereum blockchain. The contracts interact with the PLONK proofs generated by the Rust components through a verification contract that is optimized for the PLONK proving system.

The verification contract is designed to be gas-efficient and supports batch verification of PLONK proofs, allowing multiple proofs to be verified in a single transaction. This helps to reduce the overall cost and improve the throughput of the system.

Trusted Setup Ceremony

As PLONK requires a trusted setup for the universal SRS, a multi-party computation (MPC) ceremony is conducted to generate the SRS. The ceremony involves multiple participants from different organizations and backgrounds, ensuring that no single party has control over the entire setup process.

The MPC ceremony is organized and facilitated using secure computation frameworks, such as the ZEXE library, which provides a set of tools and protocols for conducting distributed key generation and parameter setup.

Concise Example: Private Asset Transfer

In a private asset transfer, Alice can transfer assets to Bob without revealing the transaction details to the public. Using PLONK, Alice generates a proof π that verifies the validity of the transfer and her sufficient balance without disclosing the transaction amount Δ.

Transfer T = (A, B, \pi) where \pi is the PLONK proof

\pi \leftarrow \text{generateProof}(A, B, \Delta)
Submit (A, B, \pi) to the transfer contract
Contract verifies \pi
- If \pi is valid, execute transfer from A to B
- Else, reject transfer

The proof \pi ensures the following conditions:

B_A \geq \Delta (Alice’s balance is sufficient)
B_A' = B_A - \Delta (Alice’s updated balance)
B_B' = B_B + \Delta (Bob’s updated balance)

The smart contract executes the transfer only if the proof is valid, ensuring the transfer’s legitimacy without revealing the transaction details.

By leveraging PLONK, the proposed decentralized payment network achieves a balance between privacy, scalability, and ease of implementation. The universal and updateable nature of PLONK, combined with the optimization techniques and secure trusted setup ceremony, provides a solid foundation for building a privacy-focused and efficient payment system.

Use Cases for Privacy

Confidential Voting Systems

Confidential voting systems are a critical use case for enhanced privacy in decentralized networks. Voting systems must ensure that each vote is anonymous and secure while maintaining the integrity and transparency of the election process. By leveraging zk-SNARKs, our network can provide a solution that guarantees the confidentiality of votes while allowing for public verification of election results.

In a confidential voting system built on the proposed network, voters would cast their votes through private transactions, with zk-SNARKs proving that each vote is valid and belongs to an eligible voter without revealing the voter’s identity. The votes would be tallied through a series of confidential transactions, with the final result verifiable through the aggregated Merkle roots stored on-chain. This approach ensures that the voting process is transparent and auditable while preserving the privacy of individual voters.

Private Asset Transfers

Private asset transfers are another significant use case for enhanced privacy in a decentralized network. These transfers require confidentiality to protect the financial privacy of users, ensuring that transaction details remain private while the integrity of the transfer is verifiable.

With the proposed network, users can transfer assets through confidential payment channels, with zk-SNARKs proving the validity of the transactions without revealing the amounts or the identities of the parties involved. This feature is particularly valuable for businesses and individuals who wish to keep their financial transactions private, such as in the case of sensitive business deals, wealth management, or personal remittances.

Secure Health Records Management

Secure health records management is an essential use case for enhanced privacy, where sensitive health information must be kept confidential while ensuring that authorized parties can verify the records. Using zk-SNARKs, the proposed network can enable the secure storage and sharing of health records while maintaining patient privacy.
In this use case, health records would be stored off-chain, with zk-SNARKs proving the authenticity and integrity of the records without revealing their contents. Patients can grant access to their records to authorized parties, such as healthcare providers or insurance companies, through private transactions. The authorized parties can then verify the records’ authenticity using the zk-SNARK proofs, ensuring that the records have not been tampered with while preserving patient confidentiality.

Global Payment System

A global payment system is perhaps the most scalable and impactful use case for a decentralized network with enhanced privacy. Such a system must provide sufficient privacy to protect user transactions while ensuring transparency and scalability to facilitate mass adoption. By leveraging zk-SNARKs, the proposed network can achieve a balanced privacy level that ensures transaction confidentiality without hindering scalability or regulatory compliance.

In a global payment system built on the proposed network, users can transact through confidential payment channels, with zk-SNARKs proving the validity of transactions without revealing the amounts or the identities of the parties involved. This privacy level can be customized based on the specific requirements of different jurisdictions, ensuring compliance with local regulations while still preserving user privacy.

To facilitate cross-border transactions and enable seamless interoperability with existing payment systems, the network can integrate with traditional financial institutions and payment processors through secure off-chain communication channels. These channels can leverage zk-SNARKs to prove the authenticity of transactions and balances without revealing sensitive information, enabling a hybrid approach that combines the benefits of decentralized privacy with the reach and stability of established financial networks.

By leveraging zk-SNARKs in these use cases, the proposed decentralized payment network can provide enhanced privacy and scalability, making it suitable for a wide range of applications. These examples illustrate how the network can achieve a balance between privacy and transparency, facilitating mass adoption while maintaining the necessary confidentiality.

Conclusion

The proposed decentralized payment network offers:

Higher Throughput: Comparable to or exceeding state channels and rollups.
Instant Finality: Superior to Optimistic Rollups.
Cost Efficiency: Reduces on-chain interactions and eliminates mining.
Enhanced Privacy: Matches or surpasses ZK-Rollups.

The unique combination of features in the proposed network makes it a potentially more scalable and private solution compared to existing Layer 2 systems.
By leveraging zk-SNARKs in these use cases, we can provide enhanced privacy and scalability, making our decentralized network suitable for a wide range of applications. These examples illustrate how the network can achieve a balance between privacy and transparency, facilitating mass adoption while maintaining the necessary confidentiality.

References

Poon, J., & Dryja, T. (2016). The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments. Lightning Network Whitepaper. https://lightning.network/lightning-network-paper.pdf
Buterin, V., & Poon, J. (2017). Plasma: Scalable Autonomous Smart Contracts. Plasma Whitepaper. https://plasma.io/plasma.pdf
Raiden Network Team. (2017). Raiden Network: Fast, Cheap, Scalable Token Transfers for Ethereum. Raiden Network
Celer Network. (2019). Celer Network: Bring Internet Scale to Every Blockchain. Celer Network Whitepaper. https://www.celer.network/doc/CelerNetwork-Whitepaper.pdf
PLONK Documentation. (n.d.). ZK-SNARKs: PLONK. Retrieved from https://docs.plonk.cafe/
Ben-Sasson, E., Chiesa, A., Tromer, E., & Virza, M. (2014). Scalable Zero-Knowledge via Cycles of Elliptic Curves. In International Cryptology Conference (pp. 276-294). Springer, Berlin, Heidelberg.
Groth, J. (2016). On the Size of Pairing-based Non-interactive Arguments. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 305-326). Springer, Berlin, Heidelberg.
Zhang, F., Cecchetti, E., Croman, K., Juels, A., & Shi, E. (2016). Town Crier: An Authenticated Data Feed for Smart Contracts. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (pp. 270-282).
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., & Virza, M. (2015). SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge. In Annual Cryptology Conference (pp. 90-108). Springer, Berlin, Heidelberg.
Hioki, L., Dompeldorius, A., & Hashimoto, Y. (2024). Plasma Next: Plasma without Online Requirements. Ethereum Research. Retrieved from Plasma Next: Plasma without Online Requirements

cryptskii · June 7, 2024, 6:46am

@vbuterin @JustinDrake @leohio . I believe this is the highest degree of “trustless” thats ever been conceptualized. Trusting in only pure math and cryptography while maintaining decentralized validity checks open to anyone. Is this not the gold standard that Satoshi invented Bitcoin for hoping to achieve? To remove the need for trusted intermediaries completely?

MicahZoltu · July 20, 2024, 4:39am

Maybe I missed it (post was very long, I scanned over some parts), but I didn’t see how transaction ordering is handled? The number one problem that blockchain consensus systems solve is transaction ordering, everything else is on top of that, so that cannot be hand waved over.

If two conflicting transactions show up on the network at the same time on different sides of the globe, half of the network will see one first and half will see the other first. How do you determine which one will occur first (and thus be valid)?

cryptskii · August 21, 2024, 11:36am

Micah,

Thank you for your insightful question about transaction ordering in our proposed decentralized payment network. You’re right that transaction ordering is a fundamental problem in blockchain systems, and I apologize if this wasn’t clear in the initial description. Let me explain how our system addresses this crucial issue.

My approach to transaction ordering combines several mechanisms:

Hierarchical Smart Contract Structure
Sequence Numbers for Local Ordering
Merkle Tree Aggregation
Epidemic Storage with Heartbeat Mechanism

Here’s how these elements work together to solve the ordering problem:

Local Ordering (Within Channels):
- Each transaction within a payment channel is assigned a strictly increasing sequence number.
- Wallet contracts ensure these sequence numbers are valid before processing transactions.
Intermediate Level Ordering:
- Intermediate contracts aggregate states from multiple wallet contracts using Merkle trees.
- This provides an ordering for transactions across different channels managed by an intermediate contract.
Global Ordering:
- Root contracts periodically aggregate Merkle roots from intermediate contracts and submit a final root to the blockchain.
- This submission creates a global checkpoint that orders all included transactions.
Conflict Resolution:
- In case of conflicting transactions, the epidemic storage mechanism with heartbeats helps quickly propagate information across the network.
- The first transaction to be included in a Merkle tree update at the intermediate contract level is considered valid.
Network Partitions:
- The epidemic storage ensures that even if the network is temporarily partitioned, the states will eventually converge.
- Heartbeat mechanisms help quickly detect and respond to network issues or node failures.

Here’s a simplified code example that illustrates these concepts:

import hashlib
import time
from typing import Dict, Set, List

class Transaction:
    def __init__(self, tx_id: str, sender: str, receiver: str, amount: int, sequence: int):
        self.tx_id = tx_id
        self.sender = sender
        self.receiver = receiver
        self.amount = amount
        self.sequence = sequence

class WalletContract:
    def __init__(self, wallet_id: str):
        self.wallet_id = wallet_id
        self.balance = 1000  # Initial balance
        self.sequence = 0
        self.transactions: List[Transaction] = []

    def execute_transaction(self, tx: Transaction) -> bool:
        if tx.sequence != self.sequence + 1 or tx.amount > self.balance:
            return False
        self.sequence = tx.sequence
        self.balance -= tx.amount
        self.transactions.append(tx)
        return True

    def get_state_root(self) -> str:
        return hashlib.sha256(str(self.transactions).encode()).hexdigest()

class IntermediateContract:
    def __init__(self, contract_id: str):
        self.contract_id = contract_id
        self.wallet_roots: Dict[str, str] = {}

    def submit_wallet_root(self, wallet_id: str, root: str):
        self.wallet_roots[wallet_id] = root

    def get_intermediate_root(self) -> str:
        return hashlib.sha256(str(self.wallet_roots).encode()).hexdigest()

class RootContract:
    def __init__(self):
        self.intermediate_roots: Dict[str, str] = {}
        self.global_root = ""

    def submit_intermediate_root(self, contract_id: str, root: str):
        self.intermediate_roots[contract_id] = root

    def update_global_root(self):
        self.global_root = hashlib.sha256(str(self.intermediate_roots).encode()).hexdigest()

class Node:
    def __init__(self, node_id: str):
        self.node_id = node_id
        self.wallets: Dict[str, WalletContract] = {}
        self.intermediate_contract = IntermediateContract(node_id)
        self.neighbors: Set[str] = set()
        self.last_heartbeat: Dict[str, float] = {}

    def add_wallet(self, wallet_id: str):
        self.wallets[wallet_id] = WalletContract(wallet_id)

    def process_transaction(self, tx: Transaction) -> bool:
        if tx.sender in self.wallets:
            success = self.wallets[tx.sender].execute_transaction(tx)
            if success:
                self.update_intermediate_contract()
            return success
        return False

    def update_intermediate_contract(self):
        for wallet_id, wallet in self.wallets.items():
            self.intermediate_contract.submit_wallet_root(wallet_id, wallet.get_state_root())

    def send_heartbeat(self, network: Dict[str, 'Node']):
        for neighbor_id in self.neighbors:
            network[neighbor_id].receive_heartbeat(self.node_id, self.intermediate_contract.get_intermediate_root())

    def receive_heartbeat(self, sender_id: str, state_root: str):
        self.last_heartbeat[sender_id] = time.time()
        if state_root != self.intermediate_contract.get_intermediate_root():
            self.request_sync(sender_id)

    def request_sync(self, node_id: str):
        print(f"{self.node_id} requesting sync with {node_id}")

class Network:
    def __init__(self, num_nodes: int):
        self.nodes: Dict[str, Node] = {f"node_{i}": Node(f"node_{i}") for i in range(num_nodes)}
        self.root_contract = RootContract()

    def connect_nodes(self, node1_id: str, node2_id: str):
        self.nodes[node1_id].neighbors.add(node2_id)
        self.nodes[node2_id].neighbors.add(node1_id)

    def process_global_transaction(self, tx: Transaction):
        for node in self.nodes.values():
            if node.process_transaction(tx):
                return True
        return False

    def update_global_state(self):
        for node in self.nodes.values():
            self.root_contract.submit_intermediate_root(node.node_id, node.intermediate_contract.get_intermediate_root())
        self.root_contract.update_global_root()

    def send_heartbeats(self):
        for node in self.nodes.values():
            node.send_heartbeat(self.nodes)

# Usage
network = Network(num_nodes=3)
network.connect_nodes("node_0", "node_1")
network.connect_nodes("node_1", "node_2")
network.connect_nodes("node_2", "node_0")

for node in network.nodes.values():
    node.add_wallet("wallet_A")
    node.add_wallet("wallet_B")

tx1 = Transaction("tx1", "wallet_A", "wallet_B", 50, 1)
tx2 = Transaction("tx2", "wallet_A", "wallet_B", 30, 2)

print("Processing tx1:", network.process_global_transaction(tx1))
print("Processing tx2:", network.process_global_transaction(tx2))

network.update_global_state()
network.send_heartbeats()

print("Global root:", network.root_contract.global_root)

This example demonstrates:

Local ordering within wallet contracts using sequence numbers.
Aggregation of wallet states at the intermediate contract level.
Global state updates through the root contract.
A basic epidemic storage mechanism with heartbeats for consistency and quick conflict detection.

Regarding your specific scenario of conflicting transactions appearing simultaneously on different sides of the globe:

The epidemic storage mechanism ensures rapid propagation of transactions across the network.
Nodes use heartbeats to quickly detect state discrepancies and initiate synchronization.
The first transaction to be included in an intermediate contract’s Merkle tree update is considered valid.
If truly simultaneous, the deterministic nature of Merkle tree construction ensures consistent ordering across the network.
The periodic global root updates by the root contract provide final confirmation of the global transaction order.

The deterministic nature of Merkle trees is a key feature that ensures consistency and reliability in our decentralized payment network. Here’s a detailed explanation:

Merkle Tree Structure:
A Merkle tree is a binary tree where each leaf node contains the hash of a data block (in our case, a transaction), and each non-leaf node contains the hash of its child nodes’ hashes.
Deterministic Construction:
The process of building a Merkle tree is entirely deterministic. Given the same set of input data (transactions) in the same order, the resulting Merkle tree and its root hash will always be identical, regardless of where or when it’s constructed.
Hash Function Properties:
Merkle trees use cryptographic hash functions (like SHA-256) which have several important properties:
- Deterministic: The same input always produces the same output.
- Collision-resistant: It’s computationally infeasible to find two different inputs that produce the same hash output.
- Avalanche effect: A small change in the input results in a significantly different hash output.
Ordering Significance:
The order in which transactions are added to the Merkle tree directly affects the final Merkle root. This property is crucial for transaction ordering in our system.
Consistency Across the Network:
Because of this deterministic nature, all nodes in the network that receive the same set of transactions in the same order will independently construct identical Merkle trees with the same root hash.

Let’s illustrate this with a code example:

import hashlib

def hash_data(data: str) -> str:
    return hashlib.sha256(data.encode()).hexdigest()

class MerkleNode:
    def __init__(self, left, right, value: str):
        self.left = left
        self.right = right
        self.value = value

def build_merkle_tree(transactions: list) -> MerkleNode:
    nodes = [MerkleNode(None, None, hash_data(tx)) for tx in transactions]
    
    while len(nodes) > 1:
        new_level = []
        for i in range(0, len(nodes), 2):
            left = nodes[i]
            right = nodes[i + 1] if i + 1 < len(nodes) else left
            new_value = hash_data(left.value + right.value)
            new_level.append(MerkleNode(left, right, new_value))
        nodes = new_level
    
    return nodes[0]  # Root of the Merkle tree

# Example usage
transactions1 = ["tx1: Alice pays Bob 50", "tx2: Charlie pays David 30", "tx3: Eve pays Frank 20"]
transactions2 = ["tx2: Charlie pays David 30", "tx1: Alice pays Bob 50", "tx3: Eve pays Frank 20"]

root1 = build_merkle_tree(transactions1)
root2 = build_merkle_tree(transactions1)  # Same order as transactions1
root3 = build_merkle_tree(transactions2)  # Different order

print("Root 1:", root1.value)
print("Root 2:", root2.value)
print("Root 3:", root3.value)
print("Root 1 == Root 2:", root1.value == root2.value)
print("Root 1 == Root 3:", root1.value == root3.value)

This example demonstrates several key points:

Identical Inputs Produce Identical Outputs:
root1 and root2 will have the same value because they’re constructed from the same transactions in the same order.
Order Matters:
root3 will have a different value from root1 and root2 because the transactions are in a different order, even though they contain the same set of transactions.
Deterministic Construction:
The build_merkle_tree function will always produce the same result for the same input, regardless of when or where it’s run.

Implications for Our System:

Consistent Global Ordering:
When nodes receive transactions, they add them to their local Merkle trees. The deterministic nature ensures that all nodes will arrive at the same Merkle root if they process the same transactions in the same order.
Conflict Resolution:
In case of conflicting transactions, the first one to be included in the Merkle tree (and thus affect the Merkle root) is considered valid. All nodes will independently come to the same conclusion about which transaction was first.
Efficient Verification:
Nodes can efficiently verify the integrity and order of transactions by comparing Merkle roots, without needing to transmit entire transaction sets.
Scalability:
The Merkle tree structure allows for efficient updates and proofs, enabling our system to handle a large number of transactions while maintaining consistency.
Auditability:
The deterministic nature allows for easy auditing. Given a set of transactions, anyone can reconstruct the Merkle tree and verify its correctness.

This deterministic property of Merkle trees is fundamental to ensuring that our decentralized payment network maintains a consistent global state across all nodes, even when processing transactions concurrently across different channels and intermediate contracts. It provides a robust foundation for ordering transactions without requiring a traditional consensus mechanism for every single transaction.

How this system maintains decentralization:

Distributed Validation: Every node in the network can independently validate transactions and state updates using the same deterministic rules.
No Central Authority: There’s no central authority controlling transaction ordering or state updates. The system relies on cryptographic proofs and predetermined rules encoded in smart contracts.
Open Participation: Anyone can potentially run a node, participate in transaction processing, or deploy their own set of contracts within this framework.
Consensus Through Cryptography: Instead of relying on a traditional consensus mechanism that might be influenced by a small group, this system uses cryptographic proofs to ensure agreement on the state.

This approach provides a scalable, decentralized solution to the transaction ordering problem without relying on traditional consensus mechanisms. It leverages the hierarchical structure and cryptographic proofs to achieve agreement on transaction order.

I hope this clarifies how our system addresses the critical issue of transaction ordering. Please let me know if you have any further questions or need additional clarification on any aspect of the system.

MicahZoltu · August 21, 2024, 11:56am

Who does this assignment, and how do they choose which of two competing transactions to prefer?

cryptskii · August 21, 2024, 12:38pm

Great questions! Let me break this down for you and share some interesting insights we’ve developed.

Firstly, addressing your question about transaction assignment and conflict resolution:

In this system, transaction assignment is handled deterministically by smart contracts. Each transaction is assigned to a specific wallet contract based on the sender’s address. For conflict resolution, like in the case of a double-spend attempt, here’s what happens:

The smart contract receives all relevant transaction proofs.
It verifies each proof cryptographically.
If there’s a conflict (e.g., two transactions trying to spend the same funds), the contract applies a deterministic rule to choose which transaction to process. This could be based on:
- First-come-first-served
- Transaction timestamp
- Lower hash value of the transaction

Only the chosen transaction is executed and recorded on-chain. The unchosen transaction is rejected, and there might be penalties for attempting double-spends.

Now, here’s where it gets interesting. I’ve been exploring an innovative approach to prevent double-spending while maintaining fairness and accessibility: a 50% spending rule for off-chain transactions. Here’s how it works:

In off-chain channels, users can only spend up to 50% of their current balance in a single transaction.
This makes major double-spend attempts impossible within the off-chain system.
It’s fair because it applies equally to all users, regardless of their total balance.
Even users with small balances can participate in transactions.

Importantly, there’s a strong deterrent against attempting to cheat the system:

If a double-spend attempt is detected, the balance that the user can’t spend (the 50% reserve) can be slashed. This serves as a powerful economic disincentive against malicious behavior.

This approach naturally segregates transactions:

Smaller, frequent transactions happen off-chain, benefiting from speed and low fees.
Larger transactions that exceed the 50% limit move to the main chain.

This creates a hybrid system that leverages the strengths of both off-chain and on-chain transactions:

Off-chain channels (with 50% rule):
- Ideal for everyday, smaller transactions
- High speed, low fees
- Prevents large-scale double-spending
On-chain transactions:
- For larger amounts exceeding the 50% limit
- Full blockchain security
- Allows full balance utilization when needed

This tiered approach offers several benefits:

Improved scalability: Off-chain handles bulk of small transactions, reducing blockchain congestion
Cost-efficiency: Small transactions get near-zero fees off-chain
Balanced security: Sufficient for daily transactions off-chain, full security for critical transactions on-chain
Accessibility: Low-balance users can participate actively off-chain
Strong deterrence: The slashing mechanism discourages any attempts at cheating

The system would automatically route transactions to either the off-chain channel or the main chain based on the amount and available balances. Users might need to manage their off-chain balances, but this could be largely automated. This approach should I believe,create a natural and efficient division of transactions, aligning with the strengths of both off-chain and on-chain systems.

MicahZoltu · August 21, 2024, 12:48pm

First-come-first-served and transaction timestamp assumes you already have an ordering/timestamping system in place, but this proposal allegedly replaces the need for an ordering system.

“Lower hash value” works, but it means the user can do controlled replacement by submitting a lower hash value transaction after the higher hash value transaction.

cryptskii · August 21, 2024, 12:57pm

Where in the proposal does it say that it replaces the need for an ordering system?

cryptskii · August 21, 2024, 1:05pm

I believe there are a few misunderstandings that I’d like to clarify:

Ordering System vs. Traditional Consensus:
You’re correct that this system doesn’t replace the need for an ordering system entirely, although, that was never a claim. What it replaces is the need for traditional consensus mechanisms like Proof of Work or Proof of Stake for every transaction. The system still maintains order, but in a more efficient, hierarchical manner.
Timestamp and First-Come-First-Served:
The system does have mechanisms for ordering transactions, but these are primarily handled at the channel and intermediate contract levels, not globally for every transaction. The hierarchical structure (wallet, intermediate, and root contracts) provides a framework for maintaining order without requiring global consensus for each transaction.
Prevention of Controlled Replacement:
Your concern about controlled replacement using lower hash values is valid in systems without additional protections. However, this system has safeguards against such attacks:

a) zk-SNARKs: Each transaction is accompanied by a zero-knowledge proof that verifies its validity and its place in the transaction sequence. These proofs are computationally binding, making it infeasible to create valid proofs for conflicting transactions.

b) Channel State: Transactions update the channel state, which is included in subsequent proofs. A later transaction with a lower hash couldn’t replace an earlier one because it wouldn’t match the current channel state.

c) Sequence Numbers: Transactions within a channel use sequence numbers, preventing out-of-order replacements.
Hierarchical Ordering:
The system maintains order at multiple levels:
- Within channels (using sequence numbers and zk-SNARKs)
- At intermediate contracts (aggregating channel states)
- At root contracts (periodically committing aggregate states to the blockchain)
50% Rule and Slashing:
Remember, the 50% spending limit in off-chain channels, combined with the slashing mechanism for detected double-spend attempts, significantly reduces the incentive and possibility for the kind of manipulation you’re concerned about.

MicahZoltu · August 21, 2024, 1:42pm

PoW/PoS (and other consensus mechanisms) are essentially just ordering/timestamping systems. If you want to replace/remove PoW/PoS you need a replacement ordering/timestamping system. If you cannot provide a complete replacement for ordering/timestamping, then you cannot remove PoW/PoS.

cryptskii · August 21, 2024, 7:24pm

I’m having trouble understanding the significance of your point within the larger context of this proposal. It seems like we’re getting caught up in semantics here…

MicahZoltu · August 22, 2024, 3:10am

Your opening claim states that you have a design for a system that doesn’t need a consensus mechanism. I’m arguing that you still need a consensus mechanism for determining order/timestamping with your design.

cryptskii · August 23, 2024, 12:08am

There. I added the word “traditional”, just for you.

MicahZoltu · August 23, 2024, 12:48am

I’m totally fine with a non-traditional consensus mechanism, but it needs to be able to fully handle ordering/timestamping for anything to work. Without that, everything breaks. Do you plan on still using PoW/PoS under the hood to achieve this, or do you have some other solution to the problem of achieving timestamping/ordering?

brentarias · August 28, 2024, 3:29pm

I very much appreciate your paper! I have many questions!

“Unilateral Payment Channel”
You have designated your Wallet Contracts as a “unilateral payment channel”. I think this means that each Wallet Contract is between exactly and only two parties (myself, and one other person). Thus if I want to send money to five different people, then I need five different Wallet Contracts. Or, in reverse, if I want to receive money from five different people - I need five different Wallet Contracts to receive the funds from them. Is that correct? It seems that the zk-SNARK proofs you used to demonstrate correct balances (viz. “Balance Consistency Theorem”) require this “only two parties” restriction. Likewise, if I’m correct, I believe this explains the confusion you had with Micah. Apparently, Micah was assuming that a single Wallet Contract is not unilateral…it can be used for sending and receiving from many recipients. If Micah were correct then, yes, the global ordering issue would then become a genuine concern…assuming that transactions are meant to be submitted asynchronously.

Rebalancing / Data Structure
When the Intermediate Contract performs a “rebalance”, I presume it’s primary duty is to update the merkle tree of the receiver. Yes? What exactly is it writing? If the sender created a transaction with sequence #23, and the receiver’s current merkle tree Wallet Contract is at sequence #15…then #23 violates the “increment by one” rule. Perhaps this can never happen, because the Wallet Contract sender/receiver is a “unilateral payment channel”…and therefore they both will always have the exact same sequence number?

Offloading zk-SNARK computation.
Is there a restriction of what device computes a zk-SNARK transaction proof? For example, if I initiate an off-chain spend from my cell phone, could my cell phone be used to compute the zk-SNARK…and then my phone sends both the transaction data and SNARK proof to the pertinent smart contract? Or is it necessary that the zk-SNARK proof is computed by the smart contract itself?

Wallet Contract Balance Visibility
When a transaction is complete, what exactly is recorded on a user’s wallet contract merkle tree? In particular, if the balance is recorded in plain text, then the transaction amount can be deduced (some privacy is lost). If the balance is not in plain text, then how does a user (such as the recipient of funds) know what their new balance is? Indeed, let’s suppose that I installed my crypto wallet on a brand new device, and provided my off-chain Wallet Contract ID. How does the network retrieve (and decrypt?) my balance? Does it copy my entire Wallet Contract merkle tree to my phone, and then my phone “walks” the data? Also, for the zk-SNARK to be computed, the receiver’s current balance also needs to be known. How do I, or how does the Wallet Contract, initially obtain and “see” the receiver’s balance?

Securing My Wallet Contract
Since my off-chain transactions are not associated with, or signed by a private key…then how do I protect someone from spending funds from my Wallet Contract? It seems someone could ask for my Wallet Contract ID, claiming they want to send me money. Once I give them my Wallet Contract ID, it seems they can then use that ID to send money to themselves from my Wallet Contract.

Purchase Book-keeping
All the transactions you demonstrate, all look like money transfers. It would be very helpful if, for example, you explained the book-keeping for how ownership of an NFT is transferred.

zk-SNARK verification gas fees
For a theoretical deployment of your off-chain solution, with Ethereum as the backing blockchain, your paper somewhat suggested the Wallet Contract and/or Intermediate Contract would run within the Eth backbone (and thus there are gas costs, such as for verifying SNARKS). If the intermediate contract is on the ETH network, and thus has gas costs for performing verification, doesn’t that at least partially defeat the purpose of off-chain transactions? If it is important for the Intermediate Contract to run on-chain, why is that so? What problems would emerge if the Wallet Contract and Intermediate Contracts were instead executed on off-chain EVM-enabled storage nodes instead of the ETH backbone?

Wallet Contract “locks”
Since all storage nodes have a copy of my Wallet Contract merkle tree, and if the off-chain storage nodes are hosting the EVM smart contracts…what mechanism decides which storage node is chosen to process my transaction? I’m asking this question, because elsewhere you say the Wallet Contract “locks” tokens to await acknowledgement from the recipient. I presume this “lock” is some kind of written state on the storage node? If I immediately make a second transaction, before the prior first transaction completed…and a different storage node is chosen to run my Wallet Contract…then the “lock” made by the previous node will not be present. In short, its not clear how to ensure the “lock” is honored.

Wallet Contract Timeouts
How might transaction “timeout periods” be monitored or enforced? Is it actively enforced (e.g. Ethereum Alarm Clock) or passively enforced (e.g. at each epoch, with an explicit scan of outstanding transactions)?

Dynamic Network?
Theoretically, can 3rd party “storage nodes” choose to join your network?

Merkle Tree Traceability
In the Q&A / comments, you provided conceptual code. That code only captured hashes of lists/dictionaries, rather than a root of a merkle tree. I presume in a real deployment, it would be an actual merkle tree root (which is itself has both a hash and navigable edges/nodes). Yes?

cryptskii · August 30, 2024, 4:07pm

Thank you very much @brentarias, for such a detailed reply post. Very much appreciated. You basically hit the head of the nail here. My post could have been clearer which resulted in the confusion here. My ownis and apologies @MicahZoltu. Im self taught and admit, I’m not the best at publishing my work.

brentarias:

“Unilateral Payment Channel”
You have designated your Wallet Contracts as a “unilateral payment channel”. I think this means that each Wallet Contract is between exactly and only two parties (myself, and one other person). Thus if I want to send money to five different people, then I need five different Wallet Contracts. Or, in reverse, if I want to receive money from five different people - I need five different Wallet Contracts to receive the funds from them. Is that correct? It seems that the zk-SNARK proofs you used to demonstrate correct balances (viz. “Balance Consistency Theorem”) require this “only two parties” restriction. Likewise, if I’m correct, I believe this explains the confusion you had with Micah. Apparently, Micah was assuming that a single Wallet Contract is not unilateral…it can be used for sending and receiving from many recipients. If Micah were correct then, yes, the global ordering issue would then become a genuine concern…assuming that transactions are meant to be submitted asynchronously.

You’re correct in your understanding. In this system, a unilateral payment channel is indeed between exactly two parties. This design choice was made to simplify the balance consistency proofs and reduce the complexity of conflict resolution.

You’re right that this means:

To send money to five different people, you would need five different Wallet Contracts.
To receive money from five different people, you would also need five different Wallet Contracts.

This design does introduce some overhead in terms of contract management but significantly simplifies the proof generation and verification process. You’re also correct that this explains the confusion with Micah’s assumption about global ordering.

Your understanding is mostly correct, but let me clarify:

When the Intermediate Contract performs a rebalance, it updates the Merkle trees of both the sender and receiver.
It writes the new balance and the new sequence number for both parties.
In a unilateral payment channel, both parties do have the same sequence number, which increments by one with each transaction.
The Intermediate Contract ensures that the sequence numbers are always in sync between the two parties in a channel.

There’s no strict restriction on what device computes the zk-SNARK proof. Your example is correct:

A cell phone could compute the zk-SNARK proof for a transaction.
The phone would then send both the transaction data and the SNARK proof to the relevant smart contract.
The smart contract would verify the proof, not compute it.

This offloading of computation is actually beneficial for scalability, as it reduces the computational load on the network.

brentarias:

Wallet Contract Balance Visibility
When a transaction is complete, what exactly is recorded on a user’s wallet contract merkle tree? In particular, if the balance is recorded in plain text, then the transaction amount can be deduced (some privacy is lost). If the balance is not in plain text, then how does a user (such as the recipient of funds) know what their new balance is? Indeed, let’s suppose that I installed my crypto wallet on a brand new device, and provided my off-chain Wallet Contract ID. How does the network retrieve (and decrypt?) my balance? Does it copy my entire Wallet Contract merkle tree to my phone, and then my phone “walks” the data? Also, for the zk-SNARK to be computed, the receiver’s current balance also needs to be known. How do I, or how does the Wallet Contract, initially obtain and “see” the receiver’s balance?

This is a nuanced issue that involves a trade-off between privacy and usability:

The balance in the Merkle tree is encrypted.
The user’s device (e.g., phone) holds the decryption key.
When installing a wallet on a new device, the encrypted Merkle tree is indeed copied to the device, which then decrypts and “walks” the data.
For zk-SNARK computation, the sender needs to know the receiver’s balance. This is handled through a secure multi-party computation protocol that allows the necessary calculations without revealing the actual balance.

The system uses a combination of approaches:

While off-chain transactions aren’t directly signed with a private key, access to the Wallet Contract is controlled by a key pair.
The Wallet Contract ID alone is not sufficient to spend funds. Any spend operation requires a valid zk-SNARK proof, which can only be generated with knowledge of the correct key.
Additional security measures like multi-factor authentication could be implemented at the wallet software level.

For NFT transfers or other non-fungible asset transactions:

The Wallet Contract would be extended to include a list of owned NFTs.
A transfer would involve updating this list on both the sender’s and receiver’s Wallet Contracts.
The zk-SNARK proof would need to verify ownership of the NFT as well as the validity of the transfer.

You raise an important point about gas fees. In practice:

The Intermediate Contract could indeed run off-chain on storage nodes to reduce gas costs.
The Root Contract, which periodically commits aggregated states to the blockchain, would still incur gas costs, but these would be amortized over many transactions.
Running Intermediate Contracts on-chain provides an additional layer of security and transparency, but as you note, it comes with gas costs. The trade-off between security and cost would need to be carefully considered based on specific use cases.

The locking mechanism is indeed a challenge in a distributed system. Here’s how it could be handled:

A consensus or randomized selection mechanism among storage nodes determines which node processes a transaction.
The chosen node applies the lock, which is then propagated to other nodes through a gossip protocol.
If a second transaction is initiated before the first is complete, it would be queued or rejected based on the detected lock.
A distributed locking protocol (like Redlock for Redis) could be adapted for this purpose.

This approach ensures that locks are honored across all nodes, preventing double-spending, and maintaining consistency.

Transaction timeout periods could be handled through a combination of approaches:

Passive enforcement: At each epoch, there’s a scan of outstanding transactions.
Active monitoring: Nodes could subscribe to events related to their open transactions.
Smart contract timers: For on-chain components, a mechanism similar to the Ethereum Alarm Clock could be implemented.

The choice between these methods would depend on the specific requirements for responsiveness and the computational resources available.

Yes, in theory, the network could be designed to allow new storage nodes to join dynamically:

New nodes would need to sync the current state of the network.
There would need to be a verification process to ensure the integrity of joining nodes.
The consensus mechanism would need to accommodate changing numbers of participants.

This could enhance the network’s decentralization and resilience, but would require careful design to maintain security and consistency.

You’re correct. In a real deployment:

It would in fact be an actual Merkle tree root, not just a hash of a list or dictionary.
This root would have both a hash and navigable edges/nodes.
This structure allows for efficient proofs of inclusion and updates to specific elements without recomputing the entire tree.

cryptskii · September 4, 2024, 4:39am

To expand the protocol for implementation on a sharded L1:

Efficient Cross-Shard Verification in zk-SNARK-based Payment Channels

In this system, each unilateral payment channel is secured and verified using zero-knowledge Succinct Non-interactive ARguments of Knowledge (zk-SNARKs). This cryptographic primitive allows us to prove the correctness of statements without revealing any information beyond the validity of the statement itself.

Formally, for each channel C_i, we maintain a state S_i which includes:

S_i = (B_A, B_B, H, n)

Where:

B_A: Balance of party A
B_B: Balance of party B
H: Cryptographic hash of the transaction history
n: Current state sequence number

For each state transition S_i \rightarrow S_{i+1}, we generate a zk-SNARK proof \pi_i such that:

\text{Verify}(\pi_i, S_i, S_{i+1}) = \text{true}

This proof \pi_i demonstrates the correctness of the state transition without revealing any information about the transaction details.

Implicit Cross-Shard Verification

The key insight of our approach is that the validity of cross-shard transactions can be implicitly guaranteed by the correctness of individual channel states. This eliminates the need for additional verification specifically for the cross-shard aspect.

Let C_i and C_j be two channels in different shards. A cross-shard transaction T_{ij} from C_i to C_j results in state transitions S_i \rightarrow S_{i+1} and S_j \rightarrow S_{j+1}. We generate proofs \pi_i and \pi_j for these transitions.

Theorem 1: If \text{Verify}(\pi_i, S_i, S_{i+1}) = \text{true} and \text{Verify}(\pi_j, S_j, S_{j+1}) = \text{true}, then the cross-shard transaction T_{ij} is valid.

Proof:
Assume, for contradiction, that T_{ij} is invalid despite both proofs being valid. This would imply that either:

The state transition in C_i is incorrect, contradicting \text{Verify}(\pi_i, S_i, S_{i+1}) = \text{true}, or
The state transition in C_j is incorrect, contradicting \text{Verify}(\pi_j, S_j, S_{j+1}) = \text{true}

Both cases lead to a contradiction, proving that T_{ij} must be valid.

Global State Representation

To efficiently represent the global state of all channels across all shards, we employ a Merkle tree structure. Let M be the Merkle tree where each leaf represents the state of a channel.

For n channels, we define:

M = \text{MerkleTree}(S_1, S_2, \dots, S_n)

The root of this Merkle tree, R_M, serves as a succinct representation of the global state:

R_M = \text{Root}(M)

This root is updated with each state change in any channel. For a state transition S_i \rightarrow S_{i+1} in channel C_i, we update the Merkle root:

R_{M_{\text{new}}} = \text{UpdateRoot}(R_M, i, S_{i+1})

System-Level Integration

When submitting the final state to the Sharded Network, we provide:

R_{M_{\text{new}}}: The updated Merkle root of the global state
\{\pi_1, \pi_2, \dots, \pi_k\}: zk-SNARK proofs for the validity of state changes in involved channels
\Delta: Minimal additional data for cross-shard transactions

Where \Delta includes:

Shard IDs involved in the transactions
Channel indices in the Merkle tree
Merkle proofs for the involved channels

Sharded Network System-Level Handling

The Sharded Network processes the submitted information as follows:

Algorithm: Sharded Network Cross-Shard Transaction Processing

Input: R_{M_{\text{new}}}, \{\pi_1, \dots, \pi_k\}, \Delta
For each proof \pi_i in \{\pi_1, \dots, \pi_k\}:
- Verify that \text{Verify}(\pi_i, S_i, S_{i+1}) = \text{true}
- If not valid, return false
Verify the Merkle root R_{M_{\text{new}}} using \Delta
- If valid, update the global state with R_{M_{\text{new}}} and return true
- Otherwise, return false

This process ensures that the Sharded Network can trust the validity of the transactions based on the zk-SNARK proofs and the consistent Merkle root.

cryptskii · September 6, 2024, 1:34pm

The Case Against Batching (Rollups)

zk-Rollups aggregate hundreds or thousands of transactions into a single batch, generating a zk-SNARK proof that validates all the transactions at once. On paper, this sounds more efficient because you’re reducing the number of proofs generated and submitted on-chain.

However, there are several key bottlenecks with this approach:

1. Latency: Delayed Finality

In a zk-Rollup system, users have to wait for the entire batch of transactions to be processed before their transaction is confirmed. This introduces a delay, which could be anywhere from seconds to minutes depending on how quickly the system aggregates transactions and produces the proof. For users seeking instant finality, this is a dealbreaker.

In contrast, per-transaction zk-SNARKs like those proposed in Overpass Channels provide instant finality. Each transaction is processed independently, so users don’t have to wait for a batch to fill up. This means that in scenarios where fast, near-instant transactions are critical (e.g., payments, gaming, real-time financial markets), a per-transaction model would outperform batch-based systems.

2. User Experience: No Real-Time Interaction

In a zk-Rollup system, users have to wait for the rollup operator to submit the batch to the blockchain. This could mean minutes of waiting for their transaction to settle on-chain. This creates a bad user experience for use cases that demand immediacy.

For example:

If you’re at a store paying with crypto, waiting for a batch to be filled, submitted, and confirmed isn’t practical.
If you’re playing a blockchain-based game, waiting for a zk-Rollup batch to finalize could ruin the experience.

Per-transaction zk-SNARKs offer instant verification and immediate finality, giving users real-time feedback that Web 2 services provide.

Why Per-Transaction Proofs Can Outperform Batching

1. Constant Complexity

In Overpass Channels, each transaction is processed individually. This means that the complexity of generating a zk-SNARK proof is constant, no matter how many users or transactions are happening simultaneously. You avoid the overhead of aggregating and verifying large batches of transactions, making it scalable in a different way.

The per-transaction model scales linearly: Each transaction is processed as soon as it occurs, with no need to wait for other transactions.
zk-SNARK generation for individual transactions in Overpass Channels is a relatively simple computation (balance updates and validity checks). As a result, this model offers predictable, low-latency performance, even as the user base grows.

2. Immediate Finality

As each transaction in Overpass Channels is verified instantly via a zk-SNARK proof, users experience instant finality. There’s no waiting for a batch to be filled and processed. This is particularly important in use cases like retail payments, online gaming, or financial trading, where instant confirmations are crucial.

3. No Operator Dependency

zk-Rollups rely on operators to collect and submit batches of transactions. This creates a potential centralization point and introduces trust issues—if the operator is slow, offline, or malicious, the entire process is delayed.

In Overpass Channels, each transaction is handled independently, eliminating the need for a centralized operator to manage batches. This creates a more decentralized and censorship-resistant system, as users aren’t reliant on a third party to process their transactions.

4. Predictable Performance

When transactions are processed individually, the system’s performance is far more predictable. Each transaction has a constant proof generation and verification time, and there are no hidden bottlenecks from waiting for a batch to be processed.

In zk-Rollups, the time to generate and verify a proof increases with batch size, making it difficult to predict how long it will take for a transaction to settle.

When Does Batching Work? And When Does It Fail?

There’s a tipping point where batching might offer performance improvements over per-transaction zk-SNARKs, but only in very specific scenarios:

If you have a small, predictable number of transactions, batching can reduce the overall on-chain cost.
If your use case doesn’t require instant finality and users can tolerate waiting a few minutes for their transactions to settle, batching could be a viable solution.

However, as you scale and as the demand for instant, real-time transactions grows, batching becomes a liability.

The transaction complexity grows with the batch size, meaning more time is needed to generate and verify proofs for large batches.
Users experience higher latency, as they have to wait for a batch to fill and be processed.

At some point, the overhead and delays from batching outstrip the benefits, especially for applications that require fast, frequent, and low-latency transactions.

cryptskii · September 12, 2024, 9:12am

Overpass Channels: Horizontally Scalable, Privacy-Enhanced, with Independent Verification, Fluid Liquidity, and Robust Censorship Proof, Payments - Low Level

[Overpass Channels Whitepaper] - High Level

cryptskii · November 9, 2024, 7:18am

Overpass is now fully open-source, and I’m seeking a few skilled developers to join the core team. Contributors can independently review the codebase, identify necessary tasks, and share a passion for advancing this project. If you’re ready to dive in and collaborate, please reach out or start contributing directly. For those unable to code for this, but still wishing to support, donations are welcome:

Ethereum (ETH): 0xDbd41D9F483691f97AFb848e997Aa6Edf6045D05

Bitcoin (BTC): bc1qtn6ufgqxc3fd8ch8xxzy4ry4epa5mcj0tagexh

Your support is greatly appreciated had to make some unique sacrifices in my scenario and age to let me do something. I really wanted to start doing so you enablers are awesome.

For those who experience a moment of eureka realization, let’s keep it a little on the quiet side for now, please and thank you. I’ve said too much already.

I’ve self-funded this project for almost two years and, as you can imagine, am now rubbing two pennies together. So, thanks to any of you who ends up showing their support in anyway they can.

GitHub: Overpass GitHub Repository