Decoy-flip-flop attack on LMD GHOST

[nrryuya]

TL;DR

We present an attack on LMD GHOST called “decoy-flip-flop” attack, by which an adversary can delay the finalization for a few hours ~ days by leveraging a network failure.
This attack does not break the basic security of ETH2.0 but implies some manipulability of LMD GHOST.

(Prerequisites: Vitalik’s blog post on LMD GHOST)

UPDATE: This research is published as a peer-reviewed paper on IEEE Access (“Impact of Saving Attacks on Blockchain Consensus”).

Setup: LMD toy consensus

To make the analysis simple, we discuss a binary consensus where honest validators try to make a consensus between two colors (RED and BLUE).
In a variant of GHOST fork-choice rule, this can be thought of as a consensus between blocks at the same height or conflicting subtrees.

• There are n validators, assume homogeneous weight (stake) for simplicity
• The time is divided into slots and epochs
  • 64 slots = 1 epoch
• Each validator is allocated into a slot for every epoch and publishes a vote in the slot
  • The slot allocation for an epoch is completed before the epoch starts
  • Assume unbiasable randomness
• Honest validators vote for the color with a greater score
  • The score is the number of validators who vote for the color in their latest message
  • When there is a tie, voters can choose one arbitrarily.

The voting rule is fundamentally the same as LMD GHOST.
Also, the slot-based voting protocol can be considered as a simplified version of ETH2.0 beacon chain.
(This is similar to “divergence game” but it’s more tricky than the games in the longest-chain rule or original (non-LMD) GHOST because scores do not grow monotonically).

Network and adversary

We consider a game between honest validators and adversary who try to prevent the consensus.

• Eventual synchrony: After some time T, the network becomes fully synchronous i.e. a message sent by an honest validator is received by any other honest validators within 1 slot.
  • We assume that at T, the winner has not satisfied the convergence condition yet.
  • In practice, this is a case when the chain does not converge by an accidental or adversary-driven network failure which lasts until T
• Adversary controls less than 1/3 of the total validators (by ratio).
• Rushing adversary: Adversary can receive all messages allocated at the slot and deliver messages to all honest validators before the next slot.
  • In practice, for instance, adversary (and also honest validators) have this ability if the network is strongly synchronous i.e. message delay is sufficiently smaller than 1 slot

In full synchrony, this voting game (and fundamentally, LMD GHOST) has a convergence condition i.e. if the set of honest validators whose latest votes support for the current winner (i.e. the color with the higher score) is larger than the half of the whole validator set, adversary cannot change the winner and hence the rest of the honest validators will also vote for the winner.

Decoy-flip-flop

We consider an adversary’s strategy called decoy-flip-flop.
Specifically,

1. The adversary keeps waiting for honest validators to vote for the winner as long as he knows the current winner does not satisfy the convergence condition after the next slot.
2. Otherwise, the adversary pivots i.e. switches all of his votes to the loser to change the winner.
3. Continue from 1.

In 2, the adversary decides whether to pivot or not before the next slot starts after seeing the result of the current slot.
The exact condition of pivoting is:
(current honest votes of the winner) + (maximum increase of honest votes of the winner in the next slot) \gt \lceil n/2 \rceil - 1.

Here (maximum increase of honest votes of the winner in the next slot) is upper bounded by the number of honest voters allocated to the next slot. If the next voters are public, this is further bounded by the number of next honest voters whose current latest votes are supporting the loser.

Savings

We assume that the adversary has earned savings before T i.e. adversary keeps being silent for e.g. a few epochs and use the rights to vote in the skipped slots (= savings) later for the decoy-flip-flop attack.

Also, since LMD GHOST only considers the latest messages, the adversary spends his savings from older slots during the continuous flip-flopping.

Simulation

I implemented the simulation of this attack in Python (GitHub Repo).

First, I did a simulation with an adversary controlling 33% of the whole validator set assuming a pubic allocation of voters.

Here is an animation of this attack.

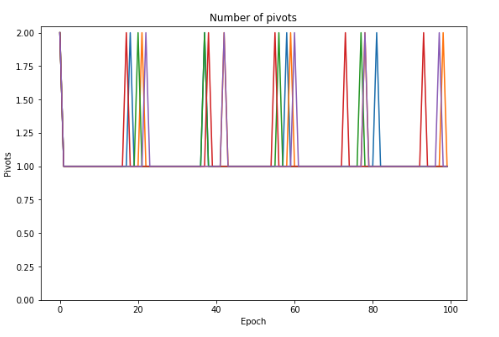
This is the number of adversary’s pivots in every epoch.

We can see (and will easily prove) that adversary must pivot for at least once per epoch.
Therefore, although new slots are allocated to adversary every epoch even during the attack, the adversary ends up publishing votes from all the slots he is allocated and hence this attack does not continue forever.

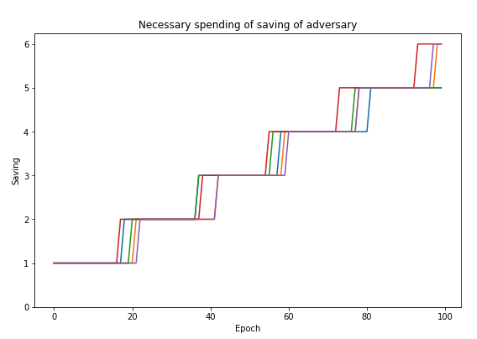
To keep flip-flopping, the adversary must prepare sufficient savings.
The next result shows the number of epochs (x-axis) for which the adversary can delay the finalization by savings he prepared (y-axis, the number of savings is measured by the number of epochs the adversary has skipped before T).

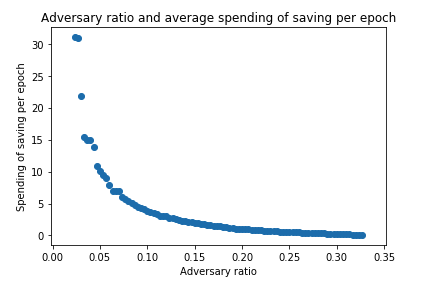
This implies that for 33% attacker, 1 epoch (6.4 minutes) of saving is sufficient to delay the convergence for more than 15 epoch (= 1.6 hours) on average.

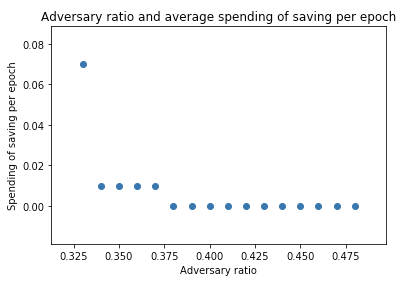
Also, we can see that the average number of saving which the adversary need to spend per epoch exponentially decreases.

In addition to these, we can observe that neither the initial state nor the total number of validators does not make a difference.

Conclusions

In summary, an adversary can extend the delay of the convergence even after a network failure, by publishing votes from the slots he skipped in the network failure.
Unlike the liveness attack on FFG by simply being silent, the adversary does not necessarily require 1/3 of the total stake.

Inactivity leak disincentivizes these liveness attacks since the adversary’s deposit is eventually slashed.
The adversary must continue to corrupt validators to keep his power and the cost of this attack increases quadratically over time.
(E.g. With the current parametrization, 33% attacker can delay the finality for a few days with the cost of 1 percent of his stake.)
In a theory of BFT consensus, this attack is more problematic since the adversary is not assumed to be rational.

CBC Casper or CBC-style enforcement of the fork-choice probably mitigate this kind of attack since an adversary must provide the appropriate evidence (“justification”) to switch chains, making it difficult to prepare for this attack.

N.B. This post & simulation has not been reviewed! I’ll appreciate any feedback/comments.

[vbuterin]

Interesting! Why are there 2 pivots required in one every 20 epochs? Also, what happens if the attacker has less than 33%?

Does the simulation account for the fact that because validators are reshuffled every epoch, some portion of validators voting for B after a pivot from A to B are replacing a previous vote that was also for B? That seems like it would dampen the effectiveness of the attack a bit.

Also, one quick mitigation I can think of is to have the fork choice rule only accept attestations from the previous or current epoch; this way you can’t “save up” votes. Would you support such a strategy?

[nrryuya]

Why are there 2 pivots required in one every 20 epochs?

The number of adversary’s pivots are probabilistically decided by the slot allocation. The more honest validators who voted for the loser in the previous epoch are allocated to the earlier slot, the faster the score of the winner grows, forcing the adversary to pivot early.

Also, what happens if the attacker has less than 33%?

As the last figure shows, the number of savings the attacker needs to prepare increases exponentially. 30% attacker is required to pivots twice every less than 5 epoch, 25% attacker every less than 2 epoch.

Does the simulation account for the fact that because validators are reshuffled every epoch, some portion of validators voting for B after a pivot from A to B is replacing a previous vote that was also for B? That seems like it would dampen the effectiveness of the attack a bit.

Not sure what you mean? In the simulation, the voters are randomly shuffled every epoch. A vote does not increase the score if the sender has voted for the color in the previous epoch.

Also, one quick mitigation I can think of is to have the fork choice rule only accept attestations from the previous or current epoch; this way you can’t “save up” votes. Would you support such a strategy?

Yeah, fresh-message-driven (FMD) GHOST will possibly work in a finality-gadget-based approach, although I haven’t analyzed it in detail. My concern is that FMD GHOST, or more generally, synchronous fork-choice rules (i.e. fork-choice rules where the scores are calculated with the assumption on timing) are not compatible with CBC Casper, where the fork-choice rule itself takes the responsibility of asynchronous finality.

[nrryuya]

Note that a large adversary can continue the decoy-flip-flop attack for a long time even without savings.
In the simulation, an adversary who controls larger than 37.5% of the validator set succeeded to delay the convergence for 100 epochs by pivoting only once every epoch.

In an extreme case, 51% attacker can make a permanent liveness failure.
Since these attacks only use the fresh votes from the current epoch, the inactivity leak does not punish the adversary.

The adversary can increase the ratio he controls by bribing other validators to join the decoy-flip-flop attack with their fresh votes. Since the bribed validators are not punished by the inactivity leak, the cost for bribing would be the reward loss + α.

[vbuterin]

When you have two pivots within one epoch, that means that all of the attacker validators pivot within that epoch, so if they do not have “savings” they all get slashed, correct?

Not sure what you mean? In the simulation, the voters are randomly shuffled every epoch. A vote does not increase the score if the sender has voted for the color in the previous epoch.

That answers my question, thanks!

Yeah, fresh-message-driven (FMD) GHOST will possibly work in a finality-gadget-based approach, although I haven’t analyzed it in detail.

So would you say that’s probably the correct thing to recommend as a “emergency fix” for phase 0 launch, given that there’s likely not enough time to spec+implement something better?

But aside from going FMD, another strategy I can think of is, what if validators locally detect which other validators are not behaving according to the fork choice rule, and locally stop taking such misbehaving validators’ messages into account in their fork choice? This seems similar to @vladzamfir’s recent approach. This way any long-term malfeasance would eventually settle into there being two chains, one attacker chain and one honest chain, and in the extreme case the social layer can favor the honest chain.

[vbuterin]

BTW I replicated the attack, here’s my python code:

import random

VOTERS = 100
ATTACKER = 25
EPOCHS = 1000

votes = [0] * (VOTERS//2) + [1] * (VOTERS//2)
attacker_side = 0
last_pivot = -1
slashed = 0
for epoch in range(EPOCHS):
    print("Epoch {}".format(epoch))
    shuffling = list(range(VOTERS))
    random.shuffle(shuffling)
    for index in shuffling:
        if index < ATTACKER:
            pass
        else:
            votes[index] = 1 if votes.count(1) > (VOTERS//2) else 0
        if votes[ATTACKER:].count(attacker_side) == VOTERS//2 - 1:
            if last_pivot == epoch:
                slashed += 1
                print("{}th slashed!".format(slashed))
            print("Pivot!")
            attacker_side = 1 - attacker_side
            votes[:ATTACKER] = [attacker_side] * ATTACKER
            last_pivot = epoch
        # print(votes.count(1), votes[ATTACKER:].count(1))
print("Slashed {} times".format(slashed))

[nrryuya]

When you have two pivots within one epoch, that means that all of the attacker validators pivot within that epoch, so if they do not have “savings” they all get slashed, correct?

Yes, in my simulation, the adversary always publishes votes from all the validators he controls in pivoting. If the adversary runs out of savings, he might continue flip-flopping only with his fresh votes (without being slashed) but the chain will converge soon unless the adversary has a high (> 33%) ratio.

So would you say that’s probably the correct thing to recommend as an “emergency fix” for phase 0 launch, given that there’s likely not enough time to spec+implement something better?

I do not come up with any fundamental flaw on FMD GHOST for now. If FMD is planned to be used for ETH2.0, I’ll try to prove it formally.

But aside from going FMD, another strategy I can think of is, what if validators locally detect which other validators are not behaving according to the fork choice rule, and locally stop taking such misbehaving validators’ messages into account in their fork choice?

Yeah, this analysis motivated me to work on Vlad’s failure rejection approach.
It’d be nice if we have a “minimum viable” failure rejection strategy for ETH2.0. The problem here is the stricter the criteria of the “correct behavior” is, the more likely honest validators mark each other as faulty by accident or network failure. Then we need some sort of “forgiveness” mechanism but it might require too big modification for Phase 0 or 1.

BTW I replicated the attack, here’s my python code:

Yep! That seems to be the same as what I described.

[vbuterin]

I would definitely not support a “grim trigger” approachg to ignoring validators that a validator deems faulty; you’re right that it’s far too error prone. What you want is something milder, eg. every “illegal” vote reduce the weight you assign them by 10%, and have the weights recover after 1 week.

The ideal end goal is that the result of any significant and large-scale validator malfeasance is that two chains, one honest and one attacker, organically form (ideally even if the attacker has >50% stake), so higher-level social consensus can pick one.

I’ll bring up LMD vs FMD in the call today.

[adiasg]

One possible Polkadot-esque solution is:

• Have validators give a succinct commitment to the justification (list of latest messages as seen by them at that moment) for their LMD messages
• Make it a slashable offence to produce messages which do not follow the LMD rule as applied on the committed justification
• When finalization is stalled for suspiciously long periods, identify misbehaving nodes and ask for the entire justification for their “pivot” messages

[vbuterin]

I guess the question is, if you have the ability to ask for and evaluate entire justifications, why not just do CBC a la https://github.com/ethereum/eth2.0-specs/issues/701 ?