Background
The common thread between Liveliness of Casper and Divergence Games and Decoy-flip-flop attack on LMD GHOST is that finding the right game theoretic framework for evaluating fork selection rules for DAG-based ledgers is difficult. One of the main difficulties in proving liveness for Capser CBC and LMD GHOST is that the current research strands do not attempt to pursue the probabilistic analysis that made the original GHOST paper useful. Unfortunately, that methodologies used for the original GHOST paper cannot be directly hoisted up to the level of DAG-based protocols for the following reasons:
- Small Network Graphs: The results hold on network graphs of two participants (or a network graph that consists of two cliques joined by a bridge), which is unrealistic for a DAG, where one hopes to have a large number of participants validating in parallel (and potentially on parallel chain tips)
- Security Parameter doesn’t scale: The paper’s model of security as a function of latency and block production rate doesn’t work in the setting where there might be multiple block production rates (e.g. due to sharding) and isn’t applicable to the high-throughput regime. This is because the paper takes advantage of analyzing the probability of quiescent periods, where no blocks are produced, to estimate the probability of a malicious fork. In the case of DAG-based protocols, there is a large spectrum of forks — some are malicious whereas others are not.
- There are too many valid topological sorts: There is not a clear ‘obviously correct’ linearizable order of blocks that have arrived. This is why the fork selection rules can be gamed and cause large reorgs. Unlike single chain protocols, DAGs have ‘good’ reorgs and ‘bad’ reorgs, in that collections of orphan blocks can become ‘better’ over time and move up in the relative ranking of linearized blocks, until they are included in the main chain. Moreover, small reorgs can be positive for DAG protocols, because they represent the linear ordering adjusting to changes in networking conditions.
The authors of the original GHOST paper, Aviv Zohar and Yonatan Sampolinsky, alleviated some of these problems for the PHANTOM protocol, where they prove asymptotic bounds on the ‘risk’ of a transaction being affected by a reorg. This risk function, which encapsulates both the safety and liveness of the protocol, is nice in that it lets one encode the partial synchrony parameters into the adversarial resistance threshold (e.g. giving a more realistic estimation of 1/4 for LMD GHOST).
Can we generalize this for other DAG protocols, including Capser CBC? This post will go through how to generalize ZS’s framework for PHANTOM to generic DAG protocols.
High-level idea
We’re going to turn the problem of estimating risk (which will be defined below) into a problem over a probability distribution over permutations of length n. This embedding will yield a probabilistic game that will separate what honest players do (e.g. correctly sampling a distribution) from Byzantine and rational players (whose objective function is antipodal to honest players). The particular distributions being sampled are a function of the blocks received by a participant and the network delay, although we will not explicitly encode this in the sequel.
Notation
Since we’re mapping the problem to the symmetric group (e.g. the discrete group of n! permutations), we will need some formal notation:
- S_n: Symmetric group on n letters
- S_A: Symmetric group on a finite universe A so that S_A \simeq S_n
- \iota_k : S_k \rightarrow S_n: The natural embedding of a permutation on k letters to one on n letters (e.g. the permutation is the identity on all elements of index > k)
- \iota_{A,B} : S_A \rightarrow S_B: For sets A \subset B, this is the natural extension of a permutation on A into a permutation on B (e.g. restricts to the identity on B - A)
- \mathsf{DAG}(n): The set of all directed acyclic graphs on n letters
- \mathsf{DAG}^{\infty} = \cup_{n\in\mathbb{N}} \mathsf{DAG}(n): The set of all DAGs on a countable number of vertices
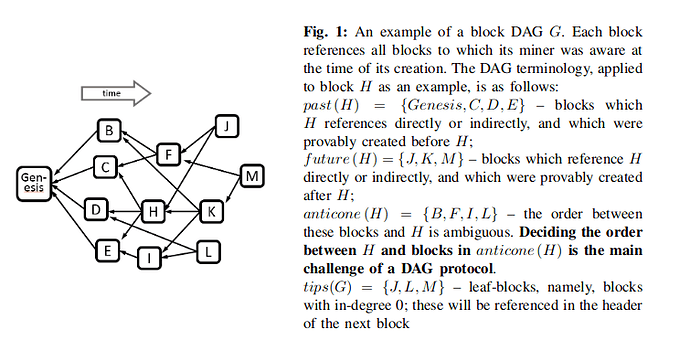
- \mathsf{Anticone} : V \times \mathsf{DAG}(V) \rightarrow 2^{V}: This is the set of blocks (represented as elements of V that are not consistent with a given block. See the figure below (from the PHANTOM paper for an example) [0].
- \mathsf{Tips}: \mathsf{DAG}(V) \rightarrow 2^{V}: This is the set of tips that a validator can grow from
- G^v_t = (V^v_t, E^v_t)\in \mathsf{DAG}^{\infty}: Participant v's DAG at time t
- G^{pub}_t \in \mathsf{DAG}^{\infty} = \cup_{v \text{ honest } } G^v_t [1]
- Given a fork choice rule (which is undefined right now), let \prec_{G^v_t} be the partial order among blocks that node v sees at time t. By construction, this is necessarily some valid topological sort of the DAG G^v_t
- \mathsf{Unif}(A): the uniform distribution on a finite set A.
Risk and Preferential Attachment
In PHANTOM, the risk associated to a block B is defined as the probability that there exists a reorg in the future such that B's relative ordering changes. Formally:
\begin{equation} \mathsf{Risk}(B, t) = \mathsf{Pr}\left[ \exists s > t, \text{ a block } C, \, B \prec_{G^{pub}_t} C \wedge C \prec_{G^{pub}_s} B \right]\end{equation}
where the probability is taken over all instantiations of the environment (e.g. over all shared and private randomness). One achieves safety and liveness if \lim_{t\rightarrow\infty} \mathsf{Risk}(B, t) = 0 for all blocks B. PHANTOM’s analysis proceeds by specializing the estimation of risk to their particular fork choice rule (‘red and blue set labelling’). We’re going to proceed by aiming to do the same analysis, but instead of focusing on their fork choice rule, describing everything in terms of permutation.
Note that the linear order \prec_{G^v_t} is equivalent to specifying an element \sigma_t \in S_{V^v_t} and that the fork choice rule also provides an ordering \prec_{Tips(G^v_t)} on \mathsf{Tips}(G^v_t). Suppose that the tips are T_1 \prec_{Tips(G^v_t)} \ldots \prec_{Tips(G^v_t)} T_k. Then we know that \sigma has the form:
\begin{align}\sigma_t &= (V_{1,1}, \ldots V_{1, i_1} T_1, V_{2,1}, \ldots, V_{2, i_2}, T_2, \ldots, V_{n, 1}, \ldots V_{n, i_n} T_n) \\ &= \prod_{i=1}^{\mathsf{Tips(G^v_t)}} (\prod_{j=1}^{i_j} V_{i, j}) T_{i} \end{align}
You can think of this as partitioning the set of blocks into a set of forks, with the fork V_{1,1},\ldots, T_1 being the most preferred fork and V_{n, 1}, \ldots, T_n being the least preferred fork. Suppose that the next block B arrives at a time s > t. What does \sigma_s look like?
Honest users usually follow a preferential attachment model [1b] — in the longest-chain world B would attach to T_1 with probability 1, whereas with other fork choice algorithms it would attach to the other tips with some non-zero probability. Thus, a fork-choice rule can also be viewed as specifying a probability distribution on tips \pi_t : \mathsf{Tips}(G^v_t) \rightarrow [0,1]. If we think of \sigma_s \in S_{V^v_s} \simeq S_{|V^v_t| +1} as a random variable, then our goal is to write the distribution of \sigma_s conditional on \sigma_t. To simplify the explanation, let’s assume that there is a fixed probability p_{\text{new}} that B starts a new fork. Thus, with probability 1-p_{\text{new}}, B joins one of the forks T_1, \ldots, T_k with probability \pi_t(T_i). Writing this as a formula gives the conditional measure:
\begin{align}\mathsf{Pr}[\sigma_s | \sigma_t] &= (1-p_{\text{new}}) \left(\sum_{k=1}^{Tips(G^v_t)} \pi_t(T_k) 1\left[ A_k \right] \right) + p_{\text{new}} 1[\sigma_t || B] \\ \\ A_{k} &= \left(\prod_{i=1}^{k-1} (\prod_{j=1}^{i_j} V_{i, j}) T_{i}\right) \left((\prod_{j=1}^{i_j} V_{k, j}) T_{k} B \right) \left(\prod_{i=k+1}^{|Tips(G^v_t)|} (\prod_{j=1}^{i_j} V_{i, j}) T_{i}\right)\end{align}
where 1[A] is the indicator function on a set A and || is the concatenation operator (thinking of permutations as strings on totally ordered sets). Note that we do not change the relative ordering of blocks between time t and s if the edit distance between \sigma_s | V^v_t (e.g. the new permutation restricted to the node set of the previous time) and \sigma_t is zero [2]. Thus, we can write a sort of minimax analogue of the above risk, in terms of this stochastic process on permutations, as (B_n is the n th block received):
\mathsf{Risk}(t) = \lim_{n\rightarrow \infty} \mathsf{Risk}(B_n, t), \;\; \mathsf{Risk}(B_n, t) = \lim_{s\rightarrow\infty} \mathsf{Pr}[ d_{edit}(\sigma_s, \sigma_t) > 0]
We can use our conditional probability measure for \sigma_s | \sigma_t to estimate this risk, regardless of fork-choice rule! The fork-choice rule shows up in computing the conditional measure as a function of the marginal distribution on tips \pi_t, which is induced via the rule.
A Game that specifies Adversarial Conditions
What is a ‘bad’ condition in the above framework? Imagine if i_1 = i_2, so that the top two forks have the same length, and that the fork-choice rule randomly chose tip T_1 over T_2 (e.g. \pi_t(T_1) = \pi_t(T_2) or ‘choosing the lowest hash’ in the random oracle model). If an adversary is able to bias the fork-choice rule into selecting T_1, T_2, T_1, T_2, \ldots, then we have a perpetual reorg, where we keep switching between branches. In fact, this is exactly what happens in Decoy-flip-flop attack on LMD GHOST. The absolute worst case is if \pi_t is the uniform distribution — then we will continuously reorg onto a variety of different forks and it will take forever to even have a convergent subsequence of two ledgers [3]. Thus we can construct conditions for a fork-choice rule that are needed for an honest majority to always have an O(\epsilon) advantage over malicious parties:
- \pi_t(T_1) - \pi_t(T_2) > \epsilon: This prevents the flip-flip with probability 1 - 2^{-O(\epsilon)}
- \forall i,j \;\; |\pi_t(T_i) - \pi_t(T_j)| > \epsilon: Ensures that there is a strong separation between all forks, which can affect high-throughput algorithms [4] which use continuously updating scoring functions to rank branches. This affects Avalanche, CBC, HashGraph, and PHANTOM and is an important design consideration
From this, we can imagine a game Uniformizer, in which an adversary attempts to force the distribution induced by the fork-choice rule to be as uniform as possible. Formally:
Game: Uniformizer
- Input: Fork-Choice rule (which induces probability distributions \pi_t)
- Honest User: Follows the preferential attachment model induced by \pi_t
- Adversary: Attempts to use stake/hash power/resource to make \pi_t as close to uniform as possible
- Social Welfare Function: Let the block arrival times be the countable sequence t_1, t_2, \ldots, t_n, \ldots \subset \mathbb{R}_{\geq 0}^{\infty} with t_i \geq t_j if i > j (this allows for halting / loss of liveness). Then our social welfare function is: \sum_{i=0}^{\infty} d_{TV}(\pi_{t_i}, \mathsf{Unif}(Tips(G^{pub}_{t_i})), where d_{TV} is the total variation distance for probability distributions. Note that the triangle inequality lets us relate this directly to the risk functions [5].
Proving incentive compliance, safety, and liveness for a fork-choice rule corresponds to proving that an adversary (rational or Byzantine) cannot win this game with advantage greater than \epsilon.
One of the main reasons for formulating everything in terms of the symmetric group is that this game naturally looks like considering the difference between a uniform random walk on the symmetric group (e.g. card-shuffling) and an adversarial walk on the group. The behavior of random (and correlated ) walks on this group is extremely well-studied by Persi Diaconis and Laurent Saloff-Coste, so these tools are probably pretty useful for proving incentive compliance, safety, and liveness in one shot.
Final thoughts
Achieving formal proofs of liveness for fork-choice rules and proving incentive compatibility are open problems for DAG structured protocols. We converted this into a game between honest agents (who faithfully sample a preferential attachment model) and adversaries who aim to steer the preferential attachment model towards a uniform attachment model. The former result in DAGs that are concentrated along one direction, whereas the latter are constant reorg’ing. This model allows for us to evaluate adversarial advantages and compare the performance of different fork-choice rules. This framework extends to other DAG protocols and hopefully provides a way to describe adversarial behaviors from first principles. I am also optimistic that this framework can be used to prove quantitative guarantees on linearizability in protocols like Avalanche. The traditional, Bitcoin Backbone view of consistency is unlikely to hold for Avalanche, so a probabilistic relaxation is necessary. If one that prove that an adversary can only win the Avalanche-instantiated version of this game for the last k blocks with high probability, then one can use this as a measure of safety/consistency for Avalanche. Note that we do not exclude rational agents — agents who are honest for some number of rounds but then mount an attack to get a fork approved — and they can be added into the framework. But, you’re unlikely to get an efficiently computable rational solution ![]()
[0] Note that in our notation, a more proper way to write the anticone is
\mathsf{Anticone}(B, G) = \text{arg}\max_{A \subset 2^{V - \{B\}}} \{ |A| : \forall \gamma \in S_A,\, \sigma\circ\iota_{A, V}(\gamma)\text{ is a valid topological sort of } G\}
Note that this maximum is unique by the properties of the boolean lattice (e.g. if there were more than one max, then their union is a max. Thus, they need to equal their union to be a maximum and hence there is only one maximum)
[1] This union is a bit weird (and somewhat sloppily used in the PHANTOM paper)— but well-defined because we cannot have any honest DAGs such that you have the same block pointing to different predecessors for honest nodes
[1b] The preferential attachment model is actually used to study random graphs that represent models of the internet graph. The famous (maybe infamous?) Barabási graph is an example of a preferential attachment model
[2] We think of the permutations as specifying strings on the finite alphabet V^v_t and compute the distance this way
[3] Note that in the ‘two forks oscillate’ example, we can eventually figure out that we’re oscillating and treat this as ‘two separate’ ledgers. If we have n forks oscillating randomly, the mixing time is significantly worse — at least by a factor of \Omega(n \log n), if they are truly random and much worse (possibly superexponentially worse!) if an adversary is clever. I always knew that the Bolzano-Weierstrass theorem would be useful in life *sarcasm*
[4] In PHANTOM, the ‘score’ for a fork is a function of a) being the longest-chain and b) how many non-chain blocks are on ‘small’ anticones. If we have a lot of flipping between forks, then this score will be unstable, which can lead to issues where an adversary can improve the ranking of a malicious fork slowly over time until they are able to (for a short while) get > 33% stake and take over the network
[5] One needs to be a bit more careful about this. In particular, the non-convex distance d_{edit} is used for risk whereas the convex, \ell^1 total variation norm is used in the sequel. Luckily, all finite dimensional norms are equivalent and Andoni’s result that edit distances can be approximated by p-norms can be used to get this result