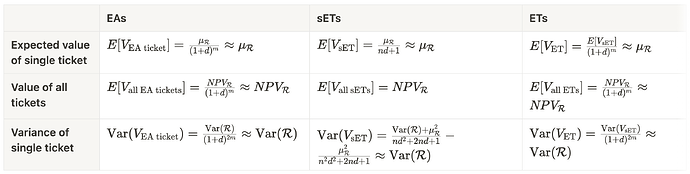Execution Auctions as an Alternative to Execution Tickets

Proof-of-Stake Block proposer
1

ealien
ealien1024×1024 128 KB


By Jonah Burian & Davide Crapis

Special thanks to Anders Elowsson, Barnabé Monnot, Justin Drake and Mike Neuder for the feedback and review.

Introduction

There is a principal-agent problem in Ethereum. While the protocol creates MEV, it leaks it to proposers. Moreover, MEV in its current state exposes the protocol to other externalities, such as timing games. It is widely held in the research community that capturing and properly redistributing MEV is an important step in the evolution of Ethereum, to make the protocol more resilient and efficient (note: there are some people who disagree). The only way to solve this principal-agent problem is for the protocol to sell the rights to earn the MEV with a credible and efficient mechanism.

After many years of research, two approaches have recently emerged as potential avenues for solving MEV-burn. These are mechanisms where the right to propose an execution payload is not given for free to the beacon proposer, but it is instead sold separately to an execution proposer.

  • Execution Auctions (EAs): The right to propose an execution payload is deterministically allocated in advance for each slot, the slot execution proposer can purchase this right by bidding in a slot auction held beforehand, for example 32 slots earlier.
  • Execution Tickets (ETs): the execution proposer right is not deterministically allocated, proposers can purchase a lottery ticket in advance and then, before each slot, a winner is drawn at random from the ticket pool and gets the right to propose.
    • The simple version of the protocol gives the winner the right to propose the following block. This was the focus of Economic Analysis of Execution Tickets.
    • The original execution ticket post suggested a general version of the protocol where the winner has the right to propose m slots later (e.g., 32). The intuition for why winners are given slots multiple slots in advance as opposed to immediately is that the solution allows for winners to offer preconfs.

The mechanisms have the same objective but important differences. The goal of this post is to compare the two solutions.

Setup

We will introduce formulas throughout this post to outline the key economic differences between the protocols. We will also explain the practical nuances, so if you want to skip the math, no worries! For the extra curious, we lay out the proof of the formulas in the appendix.

Terms

  • t — discrete time intervals (slot).
  • n — the number of tickets.
  • d is the inter-slot discount rate used to calculate the present value of future prizes.
    • Note: assuming that the vanilla staking rate is the risk-free rate in Ethereum, d \approx 10^{-8}
  • \mathcal{R} is a random variable representing the value of controlling an execution payload at time t.
    • We term this the Execution Layer Reward (EL Reward) which equals MEV + fees in slot t.
    • We assume that \mathcal{R} has a distribution that does not vary with time and that each draw is independent. (This is usually not the case in practice, as EL rewards are time-varying and correlated, but it allows for a less complicated analysis that can be expanded later.)
  • \mu_{\mathcal{R}} is the expected value of \mathcal{R}.
  • V_{ticket} — Net Present Value (NPV) of a single ticket.
    • Note: present value of some value X realized at time t is calculated as \frac{X}{(1+d)^t}.
  • m — number of slots t after winning that the right to propose is given (e.g., m=32).

Northstar

The expected net present value of all future EL Rewards is

NPV_{\mathcal{R}} = \frac{\mu_{\mathcal{R}}}{d}

This is the total value of all block space from now into the future of Ethereum. Given that the goal of the Execution Auctions and Execution Tickets is to capture the value of block space and redistribute the value to align with the protocol’s goals, all solutions must be analyzed in terms of how well they capture NPV_{\mathcal{R}}.

Note: Capturing all the value depends on the selling mechanism. In this analysis, we assume that the selling mechanism is efficient. Detailed analysis of the selling mechanism in a dynamic/repeated strategic interaction context is an open problem currently under research.

Execution Auctions

Execution Auctions (EAs) are essentially slot auctions carried out in advance:

  • Proposer right allocation: the execution proposer right for slot k+m is sold m slots in advance, at slot k.
  • Selling mechanism: the beacon proposer of slot k receives bids for that right and commits to the highest bid, attesters vote.

A secondary market will most likely develop where an EA ticket winner can resell their proposer right before their turn to propose. Even if the protocol does not allow them to transfer that right, this can be easily done via an out-of-protocol gadget.

Execution Tickets

Execution Tickets (ETs) have a lottery component that adds uncertainty on the specific block a holder will be able to propose in the future, this can be resolved closer to the time of proposing or further ahead of time.

  • Proposer right allocation: the execution proposer right for a slot in the future is sold in the form of a lottery ticket.
  • Selling mechanism: assume there are already n tickets in the lottery pool, at each slot a ticket is selected as lottery winner (e.g., at the end of the slot using RANDAO) and a new ticket is sold to enter the pool starting from the next slot.
    • Pricing: We assume an English Auction for comparison with EAs.
    • Uncertainty resolution: we can have a next-slot execution lottery, where at the end of slot k we select proposer for slot k+1 (we term these sETs i.e, simple ETs), or a future-slot execution lottery, where at the end of slot k we select proposer for slot k+m (we term these ETs).

Similarly to EAs, a secondary market will likely emerge where a ticket holder or a winning ticket holder can resell their right to participate in the lottery or propose.

Note: In the initial post Economic Analysis of Execution Tickets we did not yet make the distinction between sETs and ETs. That post was about sETs (a special case of ETs).

Note 2: Justin perceptively pointed out that we don’t know how to achieve low-latency randomness using RANDAO, and VDFs wouldn’t help either. Low-latency RANDAO would be biasable (as well as fully predictable when you control two slots in a row).

Analysis

Chart 1
Chart 12514×636 104 KB

Note: All approximations assume m (time from when the ticket wins to when the right is conferred) and n (number of ETs) are not large. Given that d is nearly zero, we are able to simplify the equations.

Note 2: Without using the approximation, EA tickets and ETs have some Dead Weight Loss associated with the fact that winning tickets cannot be immediately used, i.e., there is some loss given the time discount. The intuition for the approximation is that given d is small, this value loss due to the time discount is nominal.

Note 3: While we assume in the approximation for the variance of sETs and ETs that n is small, we discussed in “Economic Analysis of Execution Tickets” that a large n leads to less centralization risk and more democratization in terms of who can afford a ticket. That said, a large n creates valuation complexity and adds the additional complexity of having to run a large sale at the beginning of the lottery to bootstrap the ticket pool. (Read the article to learn more.)

Here is a simplified version of the chart assuming the approximation.

Chart 2
Chart 21286×464 29.2 KB

Notice that all three approaches using the approximation arrive at the same conclusion: we can effectively capture (assuming an efficient auction) all the value associated with block space. Moreover, in each design, the tickets have a simple explanation: they are worth about the value associated with proposing an execution payload.

The variance of the ticket value is the variance of the rewards per slot, which is about as good as you are going to get given that the rights to propose are sold in advance, namely prior to the block’s construction.

Sure Thing vs Future Possibility: Comparing EAs and sETs/ETs

We now turn to comparing EAs and sETs/ETs to elucidate trade-offs when thinking about implementing such mechanisms in practice. It should be noted that most of the tradeoffs stand from the fundamental difference between EAs and sETs/ETs - the former is a deterministic protocol while the latter leverages nondeterminism.

  • Implementation Simplicity: EAs are simpler to implement, the tickets do not require randomness so there is no need to worry about RANDAO bias. Moreover, it is unclear how to implement the randomness for sETs. The secondary market for proposer rights with EA tickets will be much simpler than with sETs/ETs, no need to worry about ticket MEV. Moreover, there seems to be a clear path to implement EAs via ePBS and bypassability not an issue since we’re selling future slots.
  • Simpler Assets: It is easier to reason about a deterministic asset than a random one, which makes EA better than sETs and ETS. That said, buyers in the protocol are most likely sophisticated, and the current paradigm for selecting validators relies on randomness, meaning maintaining non-determinism won’t be a substantial break from the status quo. However, a counterargument is that current proposers might not be buyers of tickets.
  • Variance could affect valuation and EA tickets are less exposed: It is reasonable for ticket holders to apply a risk discount to the tickets; that is, they might value the tickets less given risk aversion. While EA tickets are only exposed to the variance in the value of the EL rewards in slot t+m, both sETs and ETs are exposed to the variance in EL rewards and the variance in when a ticket wins. Intuitively, EA would therefore have the lowest risk discount.
  • Efficiency: From the protocol’s POV, sETs are more efficient because proposer rights are sold closer to the slot of the MEV in expectation while EAs and ETs have dead weight loss in theory. That said, when factoring in risk aversion, EAs might be more efficient.
  • Preconfs: Preconfs require there to be a lookahead, meaning the protocol must know in advance who will control the rights to the execution payload. While EAs and ETs allow for preconfs, sETs do not, as winners are decided at each block.
  • Cost-of-control:
    • In EA
      • EAs put transaction liveness risk on Ethereum—namely, the cost of monopolizing block space is disjoint from the security budget of Ethereum, and the cost of controlling consecutive blocks has a fixed value. Controlling x blocks in a row costs approximately \approx x\mu_{\mathcal{R}}. Luckily, new IL designs could rectify this. Even with ILs, relying heavily on them is suboptimal (they are designed to be a last resort, not commonplace—this can be argued). Importantly as well, the ability to consistently control multiple slots means that well-capitalized parties will perpetually win more block space. This could lead to centralization of the execution payload construction pipeline, exacerbating the current centralization challenges within this pipeline. (See the Multi-block MEV section in “Future of MEV”).
      • Barnabé aptly noted to us that saying the “the cost of monopolizing block space is disjoint from the security budget of Ethereum” is no different from the existing setup where validators can sell building rights. Currently, validators can sell multiple consecutive blocks in a row. This does not mean that the centralization argument is incorrect but indicates that EAs are not a substantial break from the status quo.
    • In sETs (and ETs):

      • While the cost of monopolizing block space is disjoint from the security budget with sETs (and ETs), it is substantially more expensive and less likely that a single party can control multiple consecutive blocks in a row. Non-determinism prevents guaranteed control over block space reducing the likelihood of control. Randomness serves as a defense against centralization.

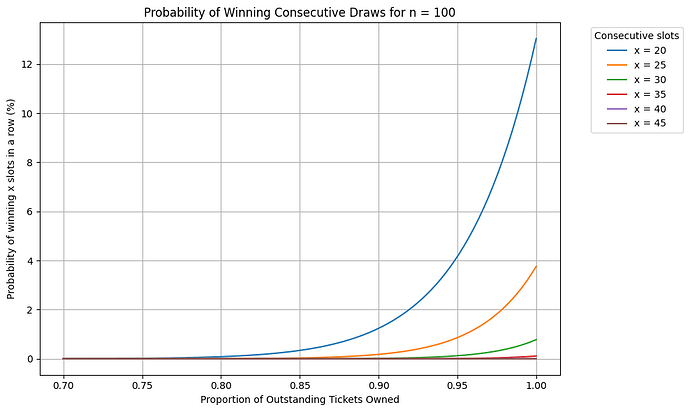
        • The first chart provides an intuitive understanding of this principle. It shows a scenario with 100 outstanding sETs/ETs. If someone owns 95% of the initial outstanding tickets (remember, one is subsequently minted per block), the probability of winning 20 slots in a row is approximately 4%, while the probability of winning 35 in a row is almost impossible.

          Graph 1
          Graph 1988×590 37 KB

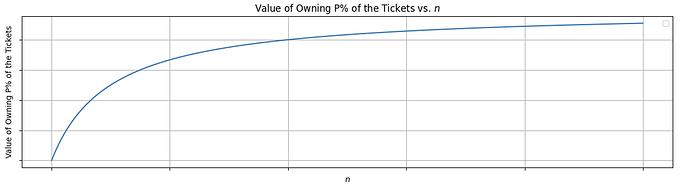
        • Moreover, the costs of controlling P\% of the blocks increases in n (See: Economic Analysis of Execution Tickets)

          Graph 2
          Graph 21380×372 18 KB

      • Where ETs differ:

        • While an attacker in sETs must rely on chance to win consecutive blocks, a clever ETs user can buy a sequence of winning tickets for t+m to t+m+x on the secondary market, making the centralization in ETs similar to the centralization problem with EAs. One can argue that sETs are subject to the same risk as an out-of-protocol auction for control of the sETs winners’ rights can happen. That said, there may be honest actors who don’t sell rights to execution payload construction. If one of these holders wins, they end the sequence of winning blocks for a sET attacker, meaning that a sET attack, even with the out-of-protocol option, is exposed to uncertainty.

Concluding Remarks

EAs dominate in simplicity, while sETs protect from centralization but at the expense of allowing for preconfs. sETs may also be unimplementable in the Ethereum Protocol today given the RANDAO problem. ILs can curb centralization concerns with EAs, and the secondary market for sETs/ETs can nullify their protective benefits. Moreover, EAs are not a substantial break from the status quo in terms of centralization.

While there are still open questions around implementing EAs and their efficiency, EAs seem to be superior to sETs and ETs for the Ethereum protocol.

Related work

This list is copied and pasted from On block-space distribution mechanisms with the addition of On block-space distribution mechanisms. lol

  1. mev-boost & relays
  2. mev-burn / mev-smoothing
  3. enshrined Proposer-Builder Separation (ePBS)
  4. block-space futures
  5. execution tickets
  6. On block-space distribution mechanisms; Mike, Pranav, & Dr. Tim Roughgarden

This post has a similar goal to Mike, Pranav, & Tim’s recent work titled On block-space distribution mechanisms: comparing new mechanisms for execution rights allocation. However, there are a few key differences in our analysis that we highlight here:

  1. They use a modified ET model (i.e., a model where all tickets are burned between slots). This model, while easier to implement, does not lead to an efficient allocation (as those with lower valuations for block space can still be allocated it).
  2. They focus on a Tullock Contest model, while our model resembles a fixed-income model.
  3. Their analysis focuses on the trade-off between the quality of the in-protocol MEV oracle and the fairness of the mechanism, while we focus on other trade-offs such as implementation ease, risk discounts, centralization control, and economic efficiency.

Appendix

Calculating the discount rate:

The staking rate at the time of this article is ~3.4% (source).

1.34=(1+d)^{\text{number of slots in a year}}=(1+d)^{365 * 24 * 60 * 60 / 12} :arrow_right: d=1.27e-08 \approx 10^{-8}

The expected net present value of all future EL Rewards:

See this paper for the proof

Calculating: E[V_{\text{EA ticket}}]

E[V_{\text{EA ticket}}] = \frac{\mu_{\mathcal{R}}}{(1+d)^m}

This is because the value is recognized m slots later so you need to discount the MEV received in m blocks by the discount rate d.

Calculating E[V_{\text{all EA tickets}}]

\begin{align*} E[V_{\text{all EA tickets}}] &= \sum_{t=1}^{\infty} \frac{ E[V_{\text{EA ticket}}]}{(1+d)^t} \\ &= \sum_{t=1}^{\infty} \frac{\mu_{\mathcal{R}}}{(1+d)^{m+t}} \\ &= \frac{1}{(1+d)^{m}} \sum_{t=1}^{\infty} \frac{\mu_{\mathcal{R}}}{(1+d)^{t}} \\ &= \frac{1}{(1+d)^{m}} NPV_{\mathcal{R}} \end{align*}

Calculating \text{Var}(V_{\text{EA ticket}})

\text{Var}(V_{\text{EA ticket}}) = \text{Var}\left(\mathcal{\frac{R}{(1+d)^m}}\right) = \frac{\text{Var}(\mathcal{R})}{(1+d)^{2m}}

Calculating NPV_{\mathcal{R}}, E[V_{\text{sET}}], E[V_{\text{all sETs}}] and \text{Var}(V_{\text{sET}})

The proofs can be found in Jonah’s “Future of MEV” paper. Remember, the paper does not make the sET vs. ET distinction.

Calculating E[V_{\text{ET}}], E[V_{\text{all ETs}}] and \text{Var}(V_{\text{ET}}),

These are simple modifications to the sET calculations using the m slot discount.

Calculating Graph 1:

The probability of winning m consecutive slots when holding p percent of the sETs/ETs initially (without rebuying a ticket each block) is determined by the product of the probabilities of winning each individual draw:

\begin{align*}W &= \left(\frac{pn}{n}\right) \cdot \left(\frac{pn-1}{n}\right) \cdot \left(\frac{pn-2}{n}\right) \cdots \left(\frac{pn-(m-1)}{n}\right) \\&= \frac{(pn)!}{(pn-m)! n^m}\end{align*}

Calculating Graph 2:

See section 4.4 in the “Future of MEV” paper.

5 Likes