By Jonah Burian & Davide Crapis
Thank you Aleks Larsen, Barnabé Monnot, Justin Drake, Mike Neuder, and others at Blockchain Capital and the Ethereum Foundation for the help.
Intro
We present an economic analysis of the Execution Tickets mechanism. We setup a framework that allows us to characterize how the value of Execution Tickets (the assets) changes with different configurations of the allocation and lottery mechanisms. We derive foundational results that have important implications when thinking about the design and the feasibility of such a mechanism for selling the right to propose an execution block in Ethereum. Our goal is to build on these results and implications as we work on validating pricing and allocation mechanism designs.
The post has three main sections: in Background Context we summarize motivations for the proposal, in Economic Analysis we setup the framework and present results and their implications, we conclude with Other Considerations that are important for practical design or to expand the analysis.
Note: in this post we present the main observations of the analysis with minimal notation. For a full formal analysis with proofs see Jonah’s “The Future of MEV” paper.
Background Context
Execution Layer Rewards
Proposers have a one-slot monopoly on block production, affording them the ability to extract two key sources of revenue: priority fees and MEV. In the future, with preconfs and based sequencing, there is a potential that this monopoly will open up additional sources of revenue.
In this analysis, Execution Layer Rewards (EL Rewards) will holistically represent all the value that can be captured from proposing a single block.
EL Reward Capture
Without external aids, proposers struggle to capture the bulk of accessible MEV. This is because effective capture necessitates sophistication given the need to optimally navigate through combinatorially complex search spaces swiftly. Acknowledging that validators might not be ideally suited for these intricate challenges, Proposer Builder Separation (PBS) has been widely embraced. This approach enables all proposers, irrespective of their level of sophistication, to capture the majority of the MEV value in their block.
PBS distinguishes the block-building function from the proposing function. Proposers can opt into an auction where builders bid for the right to choose the execution payload. Proposers then propose the execution payload with the highest associated bid. Since the builders select the payload, they receive the EL Rewards minus the bid, while the validator receives the bid. Effectively, builders are paying validators for the right to construct an execution payload. Given the competitiveness of the market and the short term monopoly the validator has on block production, the winning bid ends up being a little shy of the value of the EL Rewards.
Reassessing the Distribution of EL Rewards
This situation brings to the forefront the issue of how EL Rewards are distributed. Validators currently capture most of these rewards, but this raises questions about the optimal allocation of value within the Ethereum ecosystem. Is it more beneficial for the network’s long-term health and security if a portion of these EL Rewards is captured by the protocol itself and redirected to benefit the community more broadly? This would require somehow brokering MEV payments at the protocol level. The potential redistribution of EL Rewards could lead to a more equitable and balanced economic model within Ethereum, enhancing network security and aligning with its deflationary goals.
One approach to better distribute EL Rewards would be to enshrine PBS, also known as ePBS, at the protocol level and to burn the bid using a mechanism called MEV-Burn. While this proposal has been hotly debated, a different approach has surfaced: The Execution Tickets Mechanism.
Economic Analysis
ET Mechanism
At a high level, this mechanism splits proposers into two distinct roles: Beacon Block Proposer (BP) & Execution Block Proposer (EP) with the latter responsible for the construction of the execution payload. See a full description here. Selection for the EP occurs through a new mechanism:
- When the protocol activates, n lottery tickets are minted and can be purchased from the protocol.
- For every block, one ticket is drawn, which give its holder the right to propose.
- After the winner proposes the execution payload, the winner’s ticket is burned and a new one is minted which is available for anyone to buy.
- This process continues indefinitely.
These tickets not only confer the right to EL Rewards but also introduce a new native asset to Ethereum, potentially creating their own economy and market. Revenue from ticket sales is intended to be burned, applying deflationary pressure on ETH’s supply, increasing ETH’s value, and thereby enhancing network security.
The exact mechanism for selling these tickets is still an open research question (as the protocol will most likely only be able to capture the value of the tickets from primary, not secondary, sales).
Economic Model
Start with n tickets. A ticket provides an opportunity to win a prize (EL Reward) at discrete time intervals (slot), denoted by t. At each increment, one ticket wins. Winning results in the ticket being voided (burned) and excluded from subsequent draws. A single fresh ticket is generated (minted) following the award of the prize at each interval.
Key quantities:
- t — discrete time intervals (slot) at which prizes are awarded.
- n — the number of tickets.
- \frac{1}{n} is the probability of a single ticket winning at each time interval t.
- d is the inter-slot discount rate used to calculate the present value of future prizes.
- \mathcal{R} is a random variable representing the value of the prize (EL Reward) at time t.
- We assume that \mathcal{R} has a distribution that does not vary with time and that each draw is independent. (This is usually not the case in practice, as EL rewards are time-varying and correlated, but it allows for a less complicated analysis that can be expanded later.)
- \mu_{\mathcal{R}} is the expected value of \mathcal{R}.
- V_{ticket} — Net Present Value (NPV) of a single ticket.
- Note: present value of some value X realized at time t is calculated as \frac{X}{(1+d)^t}.
Results and Implications
We presents the main results of the analysis as a series of five findings and focus on their implications for mechanism design.
Observation 1. The expected net present value of all future EL Rewards is NPV_{\mathcal{R}} = \frac{\mu_{\mathcal{R}}}{d}
Implication: Goal Setting. This is a clear, closed-form solution for the total capturable value. The question then becomes, how much of this value can execution tickets capture?
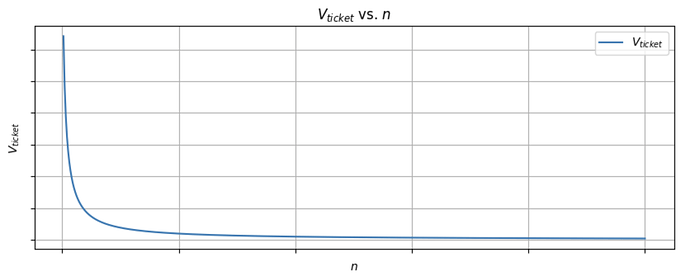
Observation 2. The expected value of a single ticket is E[V_{ticket}] = \frac{\mu_{\mathcal{R}}}{nd+1}
Implication: Breaking Information Asymmetry. Previously, \mu_{\mathcal{R}} was known ex post by all and ex ante only by highly sophisticated actors. Given the current market value and knowledge of the current discount rate, ticket sales reduce network information asymmetry by allowing the market to know the implied \mu_{\mathcal{R}} even ex ante.
Observation 3. The net present value of all tickets issued and unissued equals the expected net present value of the EL Rewards:
Implications:
- Value Capture: Assuming an efficient market pricing, Execution Tickets capture all value in the system in expectation! This means that the protocol will be able to distribute this value, instead of all of it going to the validators.
- Pricing Complexity: The effectiveness of the execution ticket system hinges critically on the method employed for setting ticket prices. It is imperative to consider the implicit discount that will inevitably factor into the pricing strategy (reflecting the operational costs, risks, and the required profit margins for execution proposers). Therefore, the pricing mechanism must be designed thoughtfully to capture as much value as possible for the protocol while still being attractive and viable for proposers. An optimal pricing strategy would aim to minimize the gap between the expected value of the tickets and the practical selling price, which would reduce the potential value leakage into secondary markets and benefit arbitrageurs over the Ethereum protocol.
Observation 4
- a) If n is sufficiently large, the current market cap of all tickets equals the present value of all future EL Reward, i.e., \lim_{n \to \infty} E[V_{\text{issued tickets}}] = NPV_{\mathcal{R}}
- b) The expected number of slots until a ticket wins is n
- c) The expected value of a ticket decreases with n
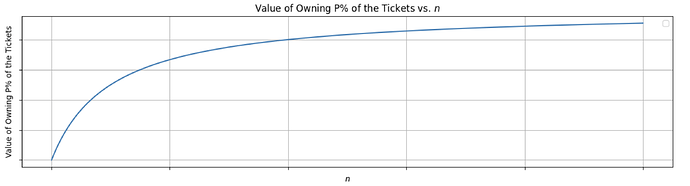
- d) The value of commanding P\% of the outstanding tickets increases in n
Implications:
-
Critical design parameter: The selection of n, representing both the initial number of tickets issued and the ongoing number of outstanding tickets per block, emerges as a critical design parameter with significant implications for the system’s dynamics and economic outcomes.
- Larger n:
- Benefits
- Less Centralization Risk: The cost of owning a significant share of tickets increases. This protects against monopolizing block construction rights and increases the cost of centralization.
- Democratization: The value, and thus the cost, of each ticket will be lower, making the market more accessible to those with less capital.
- Vanity value: as n grows sufficiently large, the current market cap of all tickets approximates the present value of all future EL Rewards.
- Problems
- Complicated Valuations: A larger n prolongs the expected timeframe for any individual ticket to win, complicating the valuation and forecasting efforts for participants. This is particularly problematic given the assumption that \mu_{\mathcal{R}}, the expected rewards, remains constant over time—an assumption that may not hold, further amplifying forecasting challenges. This uncertainty can impose a significant additional upfront discount on ticket values, allowing the secondary market to capture a large chunk of the ticket value.
- Benefits
- Small n:
- Benefits:
- Simple Valuations: A smaller n shifts more value to later sales, providing market participants with more information and potentially stabilizing the ticket market, thereby enhancing primary market value capture.
- Problems:
- More Centralization Risk
- Less Democratized
- Benefits:
- Larger n:
-
Effects of Pricing Mechanisms. Different pricing mechanisms may be employed for the initial sale of n tickets and subsequent per-block ticket sales, each with varying efficiencies in capturing the true value of a ticket. A more effective initial sale mechanism may justify a larger n, ensuring more value is captured upfront. In contrast, a superior per-block sale mechanism could justify a smaller n, facilitating an effective value capture over the long term.
Observation 5. The variance in the value of a single ticket is \text{Var}(V_{ticket}) = \frac{\text{Var}(\mathcal{R})+\mu_{\mathcal{R}}^2}{nd^2+2nd+1} - \frac{\mu_{\mathcal{R}}^2}{n^2d^2 + 2nd + 1}
Implications:
- Variance Sensitivity. Buyers may be sensitive to variance and factor it into pricing (often placing a discount).
- Valuation complexity
- Valuing tickets will be challenging due to the necessity of forecasting over an infinite time horizon. This issue is further complicated by the lumpiness of EL Rewards, i.e., the high variance of \mathcal{R} , which may change over time (contrary to the assumption). This variance contributes to the variance in the value of the ticket as \text{Var}(V_{ticket}) scales with \text{Var}(\mathcal{R}). Additionally, d will not remain static (contrary to the assumption), necessitating forecasts to account for events like rate hikes and cuts.
- Such complexity inevitably leads to the mispricing of tickets, raising concerns about whether this ticketing mechanism is purely theoretical and not suitable for practice. The primary concern lies in underpricing, which could suggest a failure to capture the intended EL Rewards. Conversely, overpricing (potentially more likely due to the speculative or gambling premium associated with the tickets) could result in capturing excess value (a scenario that might not be entirely negative since it redistributes rewards back to the protocol).
- Ticket Pooling: The emergence of ticket pooling can mitigate the impact of R's variance. By distributing rewards and variance across a pool, the system can reduce pricing complexity and could lead to more accurate ticket valuations. More work is needed to formalize the impact of pooling.
Other Considerations
Multi-Block MEV and Centralization Risks
One of the most critical challenges to this study relates to the phenomenon of multi-block MEV. This concept posits that controlling multiple consecutive blocks can yield disproportionately higher rewards than the sum of the individual blocks’ values. If multi-block MEV is prevalent (though its existence in practice is not yet clear), the advantage gained from controlling successive blocks could lead to significant, potentially exponential, centralization pressures. Multi-block MEV could lead to the formation of centralized ticket pools, with entities controlling a large number of consecutive blocks. This trend would be contrary to Ethereum’s ethos of decentralization and could pose a threat to network security. This complex dynamic suggests that if multi-block MEV does exist, it would require an entirely different model than the one proposed above to accurately factor in the greater-than-the-sum-of-its-parts effect inherent in multi-block control. The implications of such a scenario are existential and necessitate further investigation.
Related Work
This section contrasts the proposed Execution Tickets mechanism with established concepts like MEV-Burn and MEV-Smoothing, and highlights the unique advantages of the Execution Tickets approach.
- Comparison with MEV-Burn:
- Simplification: Neuder notes: “The current version of mev-burn is tightly coupled with the attesting committee for a given slot. The burning mechanism in the execution ticket design is more straightforward…"
- Timing and Value Capture:
In the simple MEV-Burn model, the amount burned equals the highest bid in the first D seconds of the auction. It is known that MEV bids increase monotonically over time because builders have more time to explore the problem space. Consequently, MEV-Burn fails to burn all potential MEV. The Execution Ticket model, conversely, captures the full MEV value, albeit in expectation. - Credible Neutrality
Another issue with MEV-Burn is its reliance on ePBS, and the problem lies in the very name — PBS is enshrined. This approach is opinionated and not credibly neutral. Better supply chains and auction systems might be discovered in the future. The ticketing system is agnostic to the method of MEV capture and simply presupposes that MEV value will flow to the execution proposer due to the proposer’s inherent block space monopoly. - Bypassability Issues:
A significant challenge with MEV-Burn is the ePBS bypassability problem. There is no credible method to ensure all proposers and builders use the protocol. The ticketing system avoids this issue by not dictating an MEV capture method. This flexibility renders the ticketing system less prone to circumvention compared to ePBS.
- Comparison with MEV-Smoothing:
-
Philosophical Considerations on Reward Distribution:
A fair argument can be made that the protocol should not intervene in artificially smoothing rewards, but allow for a free market where individuals and entities decide their own tolerance for variances in earnings. Those seeking lower variance in the proposed Execution Tickets mechanism can join ticket pools akin to the current staking pools offered by Lido and Coinbase. However, it is important to consider the potential for centralization (like what is happening with liquid staking pools). Further research is necessary to determine the viability of decentralized ticket pools.
-
Conclusion
When Execution Tickets are priced correctly they can indeed internalize all value generated from proposing execution payloads and redirect what was once validator revenue to the protocol. This is a significant breakthrough. It suggests that the contentious issue of MEV capture could potentially be resolved without necessitating ePBS.
The analysis reveals that a ticket represents a clean and elegant abstraction: a share of future EL Rewards. Such a mechanism sets the foundation for a robust market where tickets serve as leading indicators of network value generation. Moreover, as these tickets are sold prior to a block construction, the revenue generated could bolster Ethereum’s security budget in anticipation of highly volatile events.
However, the success of this mechanism hinges on the efficacy of the ticket sale process. The protocol must be capable of selling tickets at their intrinsic value; otherwise, the value would inevitably leak into a secondary market.