MEV resistant dynamic pricing auction of execution proposal rights
Execution proposal of marriage between EA and ET through an auction sequenced by RANDAO (she said yes).
By Anders. Special thanks to Barnabé for helping me improve the clarity of this post. Thanks also for valuable feedback to Thomas, Julian, and Francesco.
1. Introduction
1.1 Background
As part of the effort to enshrine proposer–builder separation (ePBS), the role of beacon validators as execution proposers has come under scrutiny. Execution tickets (ET), first introduced as attester–proposer separation, is a mechanism for selecting the execution proposer by random draw from a ticket pool, aiming to detach beacon validators from the selection process. However, the mechanism for selling tickets has not been settled, with several alternatives under consideration. A notable concern is that the sale of execution tickets may induce maximal extractable value (MEV). If the mechanism is administered by the consensus layer and the beacon proposer is given too much influence over the price or over the selection of purchasers, the design risks repeating one of the issues it was intended to resolve, with a new source of MEV becoming a concern. An execution layer vending machine raises similar questions. Therefore, a MEV resistant auction mechanism could be desirable if pursuing ETs.
Execution auctions (EA) is a related mechanism for selecting a future execution proposer, omitting the ticket pool. It relies on a MEV pricing auction, where bidders first make bids that set a floor to the MEV burn, and finally bid through tips in order to be selected by the proposer. Concerns have been raised (1, 2, 3) regarding the viability of MEV pricing auctions due to insufficient bid incentives in the initial phase. It has recently been suggested that this concern is resolved by considering the staking metagame, in which stakers must bid early to deprive other stakers of revenue. However, this resolution implies that EAs will lead to increased staker–builder integration, which might also be a cause for concern. For this reason, it seems fruitful to explore an alternative auction mechanism also when selecting the execution proposer without leveraging a ticket pool.
1.2 Overview of proposal
This post introduces a dynamic pricing auction with MEV resistance to sell execution proposal rights. Builders hold reserves in a debit account and place binding purchase order for a ticket (ET) or an execution proposal slot (similar to EA). The final price adapts dynamically based on the total outstanding as well as currently incoming orders/tickets, with some similarities to, e.g., EIP-1559, and the payment is burned. Orders are delimited at the slot level through attester observations to remove agency from the beacon proposers facilitating the auction, thus inducing less new MEV. This produces a high aggregate MEV burn. In one version of the design, dubbed execution ticket auction (ETA), orders that came in during the same slot are sequenced for proposal by leveraging the RANDAO. In another version only applicable to ETs, orders that came in during the same slot are minted collectively into tickets. Due to the current limitations of the RANDAO, the mechanism is only capable of auctioning off proposal rights at least one epoch in advance.
2. Purchase process
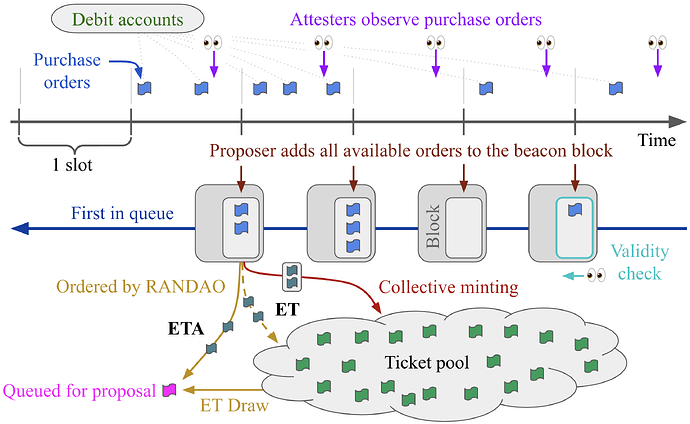
Figure 1 presents the proposed purchase mechanism. Builders send purchase orders (for one ticket/execution slot at a time) over a public P2P layer. They specify a maximum price and hold a debit account within consensus to guarantee that their purchase orders are backed by sufficient funds. This account is funded using a separate transaction (see the discussion).
Beacon attesters observe all orders up to an observation deadline, enacted for example 2 seconds before the slot boundary. The beacon proposer collects all orders (there will be one purchase order per slot on average), including orders they may have found during the last few seconds of their slot. Orders are added as a group to the beacon block and will later be popped from a virtual first-in first-out (FIFO) queue scheduled across blocks. This queue may be just one slot long, depending on implementation.
Attesters reject the block if the beacon proposer fails to include a purchase order that they observed. The mechanism thus far has similarities to MEV pricing auctions (e.g., MEV smoothing, MEV burn, EA), but attesters are tasked with simply observing all purchases, instead of setting a bid floor. Another design that might come to mind is inclusion lists (ILs) in the style of FOCIL, but there is no new active participant in the form of an IL committee.
Figure 1. Schematic overview of the purchase process. Orders in blue, backed by builders’ debit accounts, are observed by attesters (purple arrows). Beacon proposers subsequently add all incoming orders to the beacon block (dark red arrow). A validity check is performed to ensure that orders are fully backed. Orders are finally processed—using either RANDAO to determine the sequence in cases where several orders came in during the associated slot (yellow), or otherwise using collective minting (red). In ETA, orders are directly queued for proposal.
Once a slot’s orders have been added to the beacon block, a validity check is performed on builders that included at least one new order (cyan in Figure 1). If a builder’s outstanding (not yet processed) orders across the queue are not fully backed by its debit account, all the builder’s pending orders are discarded. A penalty may also be applied. Orders are priced directly upon being added or, e.g., at the time of sequencing, as described in Section 4. The determined purchase price is charged from the debit account and burned. The remaining ETH of the purchase order is subsequently virtually released such that it can be used to back new purchase orders. Orders are then sequenced and either queued for proposal (yellow arrow) or added to the ticket pool (red arrow), as described in Section 3.
3. Sequencing process
The purchase orders from the same slot are added unsequenced to the beacon block. The subsequent sequencing of orders from the same slot varies between designs.
3.1 ET – Minting of execution tickets
The natural strategy for ETs is collective minting, wherein all orders from the same slot mint a ticket at the same time, as indicated by the red arrow in Figure 1. The RANDAO used for ETA in the next subsection could also be applied to ETs using the same setup (dashed yellow arrow). However, the only real benefit (which remains marginal) is to facilitate a more even replenishment of the ticket pool.
3.2 ETA – orders sequenced by RANDAO
Purchase orders that came in during the same slot can be sequenced directly by the RANDAO, completely skipping a ticket pool. Perhaps execution ticket auction (ETA) would be a proper moniker. Indeed, with this design, a buyer will have an Estimated Time of Arrival for their order, which suitably cannot be precisely known beforehand if there is more than one order in the slot. Barnabé’s discussion (1, 2) on the topic of ETs and determinism is relevant here.
Orders can only be sequenced after the RANDAO has been updated. Therefore, there is an initial ineligibility window W during which orders cannot lead to an execution proposal. The RANDAO updates every 32 slots, but the proposed mechanism does not guarantee a new order every slot; in fact, the mode will be zero orders in a slot. Consequently, the safe distance between auction and slot proposal will need to be somewhat longer than 32 slots. Sequenced orders can be understood as sitting in a second FIFO queue while waiting to propose. Note that ETA could set the queue to hold as many proposal rights as the ticket pool, if desirable.
4. Dynamic pricing
4.1 Ticket saturation and delta
The exploration of dynamic pricing will refer to processed orders as “tickets”, although in the ETA design these are just sitting in the ordered queue waiting to propose. The protocol strives to ensure that there are \hat{T} outstanding tickets at any time. The price of a new ticket should be determined by the current number of outstanding tickets T as well as the current supply of purchases and purchase orders T_p, measured over some window of length W_T, which in some versions can be only one slot long.
Define the ticket saturation as T_s=T-\hat{T}. If T_s<0, there are too few tickets, and the protocol would in general like to sell more than one ticket per slot. If T_s>0, there are too many, and it would in general like to sell fewer than one. The delta T_{\delta}=T_p-W_T gives purchase orders relative to an expectation of one ticket per slot, which is the rate at which tickets are consumed by execution proposers. If T_{\delta}<0, the protocol is selling fewer than one ticket per slot and would in general like to sell more. If T_{\delta}>0, it sells more than one and would in general like to sell fewer.
If both T_s and T_{\delta} are negative, the protocol should decrease the ticket price to sell more tickets. If both T_s and T_{\delta} are positive, it should increase the price to sell fewer. The less trivial question is how to approach a situation when one of the variables is negative and the other is positive, how to window sales, and how quickly to adjust the price.
4.2 Dynamic pricing mechanism
4.2.1 Overview
The price of tickets adjusts on a relative basis, just like in EIP-1559, gradually shifting by some proportion of the current price each slot. To improve MEV resistance and adapt to the problem at hand, three differences to EIP-1559 however seem useful: (1) the price should depend on orders included in the current slot, not only the preceding; (2) the block should never be “full”, lest the ticket price becomes very high; (3) the mechanism should be “two-dimensional” in the sense that it accounts for both ticket saturation and delta.
This subsection begins by exploring the simplest realization of such a pricing mechanism, which will then gradually be expanded. In the simplest design, W_T=1, and orders can be priced directly when added to the beacon block. If there is one new order (T_{\delta}=0) and the number of outstanding tickets is as desired (T_s=0), the price stays the same. If there are many new orders (a sudden spike in the expected MEV), the pricing mechanism will hike the price substantially. For example, if 100 orders were to come in, the purchase price for them could rise by orders of magnitude; the exact specification would need to be determined based on other auction paramters such as the size of the ticket pool. Builders will of course track incoming orders in real time and update their estimate of the final purchase price. Therefore, even during a sudden rise in expected MEV, there will only be new orders up to the point where the deduced price matches expected MEV.
As another option, W_T can be longer, setting the price W slots after orders have been added to the beacon block. In Figure 1, W=3. An asymmetric window spanning 4 slots up to and including the processing slot is then an option. The most important benefit is MEV resistance during spikes, as will be further discussed in Section 4.3. Other potential benefits include better pricing granularity, a more complete picture when pricing orders, and the marginal simplification in ETA from pricing and sequencing orders at the same. Of course, it can be argued that the picture already is “complete” in the sense that builders can indicate expected MEV already at the current slot, albeit they may not be fully equipped to evaluate incoming orders in real-time. It can also be argued that W>0 and W_T>1 needlessly increase uncertainty and analytical complexity for builders as well as developers. As an example, builders may place an order several slots before a spike, but still need to pay closer to the real expected value of the MEV they are about to receive (priced closer to proposal time).
4.2.2 Equations
A rudimentary example will now be provided. Should this general mechanism be pursued, the exact price controller would have to be determined by reasoning about how quickly the price should adapt to changes in the willingness to buy tickets, sensitivity to ticket saturation, interplay between saturation and delta, sensitivity to MEV induction (see the next subsection), and by running simulations of the purchase process.
Ticket saturation and delta from the previous subsection is first weighed by window length and desired number of outstanding tickets
using the constants c_s=2^3 and c_{\delta}=2^6. The percentage change w to the ticket price applied each slot is
This post uses k=2, ensuring a non-linear price response as T_{\delta} grows. This can be particularly relevant at shorter windows W_T. Setting k=3 is also viable. The constant c_{\delta} can then alternatively be increased to offer better pricing granularity at a lower ticket delta, while still offering some guarantees regarding the maximum number of orders that may come in during one slot. The price p updates from its level at the previous slot p_0 to its level at the present slot p_1 as
4.2.3 Visualizations
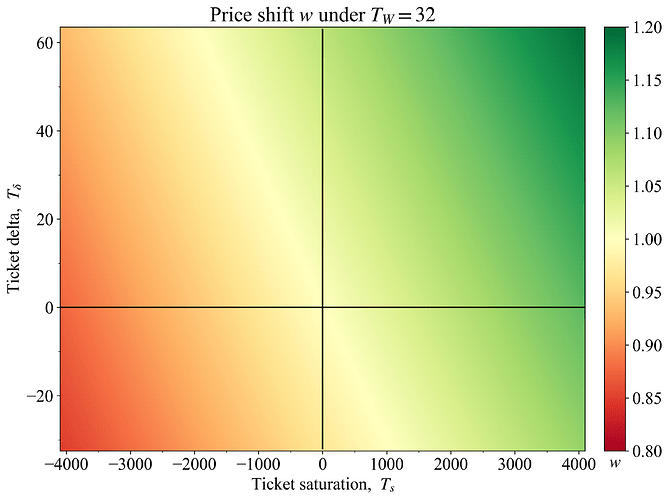
Figure 2 illustrates what a pricing schedule according to w would look like for the outlined equations, with \hat{T}=4096 and W_T=32. The yellow band stipulates no price change (w=1), and passes through the intersection of the black lines, which correspond to a neutral ticket delta (x-axis) and saturation (y-axis). There have been suggestions of much higher \hat{T}. This issue relates to a wide range of considerations that are not the focus of this post.
Figure 2. Rudimentary example for W_T=32 of a percentage change in ticket price that varies with delta in ticket sales and the overall saturation of tickets in the pool. Black lines indicate a neutral delta (one ticket sold per slot) and saturation (T=\hat{T}).
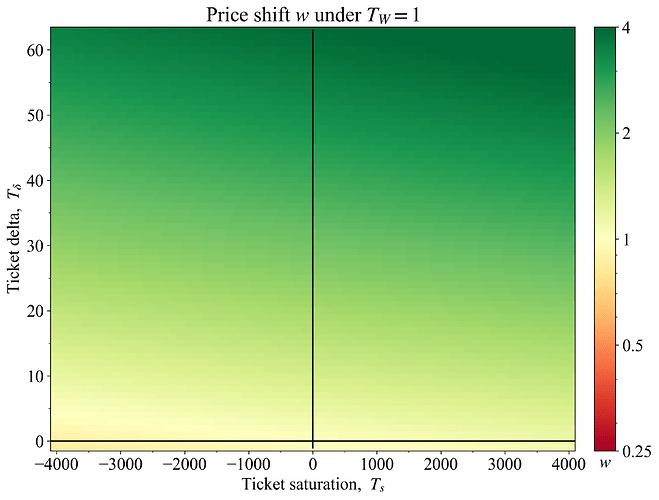
Figure 3 instead shows a pricing schedule when W_T=1 using the same equation and settings as previously. If no orders come in during the measured slot, T_{\delta}=-1. Note that the colormap is log-scaled to capture the large increase in w that is instituted if 64 orders were to come in during a single slot. When T_W=32 (Figure 2), a large jump in orders would affect the price for 32 consecutive slots (assuming an asymmetric window), before the purchase takes place, and so w will naturally be lower on a per-slot basis.
Figure 3. Rudimentary example for W_T=1 of a percentage change in ticket price that varies with delta in ticket sales and the overall saturation of tickets in the pool. Black lines indicate a neutral delta (one ticket sold in the slot) and saturation (T=\hat{T}).
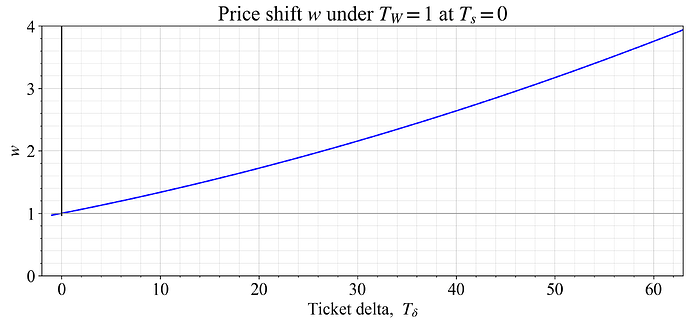
The relative change at W_T=1 for different T_{\delta} is shown in Figure 4, at a neutral ticket saturation (T_s=0). The price change instituted with this setting for between 0 to 4 orders is {0.969, 1, 1.031 1.063 1.096}. The same granularity can be preserved at lower quantities of orders while further raising the price at higher quantities, by increasing k.
Figure 4. Rudimentary example for W_T=1, focusing on the relative price change w across T_{\delta} at a neutral saturation. If 60 orders come in during a single slot, the price rises sharply.
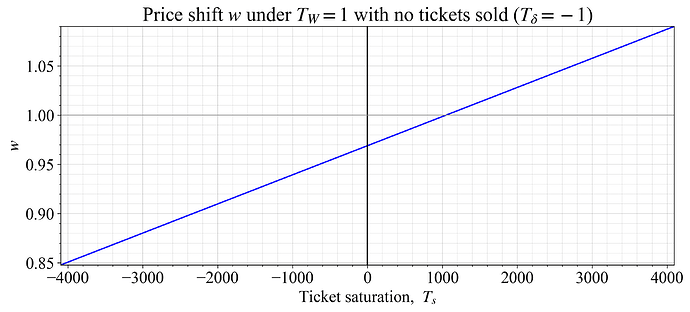
Figure 5 instead plots the response at T_{\delta}=-1 across T_s. In other words, it shows how the price would change if no purchase orders are registered.
Figure 5. Rudimentary example for W_T=1, focusing on the relative price change w across T_s when no purchase order comes in.
4.3 Windowing and slot surge pricing
In the outlined pricing mechanism, there is a remaining opportunity for the beacon proposer to derive some MEV at shorter windows T_W. This happens during a sudden spike in interest for purchasing tickets between the point where attesters have observed purchase orders and the slot boundary.
Let n_a be the equilibrium quantity of orders that would have come in during a slot if a spike happened before the attester observation deadline (purple arrows in Figure 1). Builders keep track of incoming orders and calculate the current ticket price, which when compared to the updated expected MEV V_e produces n_a orders. If a spike comes in after the attester deadline, the proposer has exclusivity and could (be paid to) include only a subset of the orders n_p. The surplus MEV for the proposer emerges from providing a lower expected purchase price for each order it lets through. This is a monopoly pricing regime, wherein the proposer sells spots at a price approaching V_e-p_1. It determines n_p to maximize its revenue R(n_p), in accordance with the revenue function:
Here, p_1(n) is based on the price equation provided in the previous subsection. Also note that if many purchase orders come in, V_e might gradually fall (if there is a temporary spike); hence V_e(n).
Quick edit: some additions/adjustments and referring to the previous subsection, which I had forgotten to do.
As mentioned in the previous subsection, longer windows W_T serve to further starve off MEV. The reason is now clear: bids of the present slot will with longer windows be priced based on information coming in also during subsequent slots. This means that the proposer has less leverage during a sudden spike, since builders will need to pay based on bids that are also observed by attesters (at the fair market price). In Figure 2, the price would be set 32 slots after inclusion in the block, influenced by the bids in these slots. Another way to achieve a similar effect without longer windows is to charge according to the price calculated during the next slot. Here it is important to note that bidders of the next slot cannot materially grief bidders of the present slot. They will also have to pay close to the price of bidders in the current slot, since the price cannot fall substantially between slots at short windows, only rise (also note the discussion of max price in Section 4.4). Yet the downside of heightened uncertainty for builders regarding pricing can be important to keep in mind.
If the price surges more quickly from a high quantity of purchased tickets within a single slot, the proposer’s potential revenue could also be reduced. Proposers can then sell fewer spots. Furthermore, by letting the price in the next slot not shift as much, oscillations in bid quantity (and potentially price) can be tempered. One way to achieve this is to let w rise more quickly with an increase in bids, set the price in the current slot as previously
but to not incorporate the full price change when setting the value p^*_0 that will be used as p_0 when pricing the next slot
The constant c_w is then set above 1. During a spike in expected value up to a new baseline V_e, the price would then theoretically stay rather fixed (at a new higher level) for subsequent slots, with the number of orders in each slot gradually decreasing, until it proceeds at the regular pace of one purchase order per slot. Yet note that if V_e rises from a temporary opportunity, there will be a bit more MEV for the proposer to extract still, because a lot of the value can depend on getting in early. This further depends on if the mechanism is ET or ETA and the size of the ticket pool. It is also important to note that a price surge means giving up some bid granularity. The discussion offers some further thoughts on bid granularity and the proposer’s ability to extract MEV.
As a concluding remark, it should always be remembered that a big ticket pool acts to temper fluctuations in the expected value of tickets. The buyer does not necessarily buy the right to sell tickets within the next couple of epochs, but rather within the next couple of hours, days, weeks or months, depending on the setting for \hat{T}—and it turns out that when measured over longer periods, the level of the MEV has been very stable in Ethereum.
4.4 The role of a maximum price
Each buyer assigns a max price to the order. This is the value that needs to be backed by the debit account. If the max price is insufficient at the time of pricing, such that the actual price is higher, the builder does not receive a ticket/slot. Yet builders could make unbacked orders to starve off competitors, which would bring down the purchase price. It seems desirable to not force builders to analyze the balances of every competitor to determine which bids are real and which are “fake”. One simple way to avoid such a situation is to penalize builders for placing orders that turn out to be unbacked at the time of purchase. This can potentially be combined with setting a validity rule requiring some minimum max price, either relative to the prevailing price at bid time, or/and as a fixed overall minimum.
Penalizing builders however exacerbates another potential issue. During an unforeseen spike in expected MEV, there are circumstances where a builder could “liquidate” its competitors’ bids if the current purchase price is close to their stipulated maximum. A builder could enter new bids forcing other builders out, to penalize them and gain cheaper tickets. For this reason, the mechanism could reduce gameability and the risks as well as improve capital efficiency for builders by stipulating an absolute maximum purchase price. A builder that bids the absolute maximum is guaranteed to not get liquidated and will always receive a ticket. This does not mean that the protocol will burn less MEV, merely that in times of extremely high expected MEV, there will temporarily be a higher quantity of bids, wherein each order has a lower chance of actually getting one of the desirable profitable slots.
What should the absolute maximum be set to if this path is pursued? In data provided by Flashbots spanning 2.7 million blocks between the last quarter of 2022 and the third quarter of 2023, the maximum average REV across 64 slots is 19.5 ETH. The peak average is skewed by a few spurious blocks with REV of several 100 ETH that may have been hard to predict beforehand. This average does therefore not represent a realistic expected MEV for builders bidding many slots in advance. Expand the window by a factor of 4 to 256 and the maximum average falls almost by a factor of 4, to 5.25. Setting the absolute maximum to 5 ETH would thus presumably not influence the auction even in times of extreme market conditions, since that price would hardly ever be reached.
5. Discussion
A MEV resistant dynamic pricing auction for selling execution proposal rights has been presented, relevant to the research of both ETs and EAs. It seeks to remove agency from the beacon proposer, thus inducing less MEV. This is achieved by having every order result in a sale, and every order coming in during the same slot having the same expected sales price. The execution ticket auction (ETA) sequences orders directly for proposal by leveraging the RANDAO. Orders that came in during the same slot can otherwise be minted collectively into tickets, with sequencing pursued at a later stage in accordance with the ET proposal.
If pursuing this auction mechanism, the dynamic pricing step would require substantial analysis. One sensitive part is the balance between moderating changes in the supply of orders while still offering sufficient pricing granularity. A high k can be useful here. Another potential avenue is to hold the auction less frequently. The expected timing of orders within the slot would also be interesting to study—orders can be placed early to starve off others, or late to gain better information. One could even theorize that some builders will wait until after the attester deadline, and then pay the proposer a small fee for exclusive post-deadline inclusion (the benefit being to avoid race conditions).
Transactions to fund or withdraw from a builder’s debit account would need to be synchronized with the validity check to avoid race conditions. It may be convenient to expand the role of the debit account if it is desirable to subject builders to slashing or penalties at the execution proposal stage. In other words, the debit account might also function as a stake.
Just as with MEV pricing auctions, attesters accepting or rejecting a block based on some observation deadline is potentially sensitive. However, this particular design should hopefully be less so, since there will only be one order on average per block to observe, and less value (even potentially negative) in bidding later in the block. A potential benefit of an auction administered instead at the execution layer is the “endogenous” component, facilitating a higher burn; the value of a ticket increases if the current ticket holder can extract value from future ticket holders through MEV. However, this direction raises gameability concerns if a single actor can come to monopolize the auction (ILs may here be useful). A MEV resistant mechanism, as here proposed, originating at the consensus layer, therefore seems like a viable direction.
It might seem tempting to replicate some facets of the proposed design for transaction processing: making the protocol more MEV resistant by having attesters observe transactions, the protocol sequence them by RANDAO, and the price adjust in a slot-delimited fashion. However, the requirements for transactions are different than for the purchase orders of execution rights analyzed in this post (e.g., time, quantity). Translating the ideas of this post directly to transaction processing might therefore unfortunately be difficult. Yet the proposed mechanism could perhaps lend some inspiration going forward.
It should be noted that multi-block MEV is a separate topic of concern. The proposed mechanism is resistant to inducing MEV at the purchase stage but does not preclude multi-block MEV. This is a general issue and an underexplored topic at this point in time. Censorship resistance is likewise an important problem not addressed by the auction mechanism. Various strategies, such as ILs (1, 2, 3), have been proposed. Whether the presented auction mechanism can be one part of an overall architecture that also tackles other issues remains to be explored.