One-bit-per-attester inclusion lists

Proof-of-Stake Block proposer
1

Inclusion lists are a technology for distributing the authority for choosing which transactions to include into the next block. Currently, the best idea for them is to have an actor that is from a set that is likely to be highly decentralized (eg. consensus block proposers) generate the list. This authority is decoupled from the right to order (or prepend) transactions, which is an inherently economies-of-scale-demanding and so likely to be highly concentrated in practice.

But what if we could avoid putting the responsibility onto a single actor, and instead put it on a large set of actors? In fact, we can even do it in such a way that it’s semi-deniable: from each attester’s contribution, there is no clear evidence of which transaction they included, because one individual piece of provided data could come from multiple possible transactions.

This post proposes a possible way to do this.

Mechanism

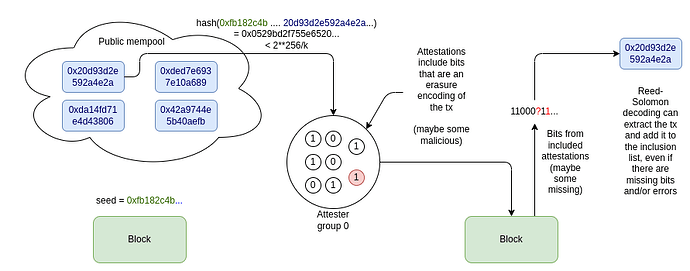
When the block for slot N is published, let seed be the RANDAO_REVEAL of the block. Suppose for convenience that each transaction is under T bytes (eg. T = 500); we can say in this initial proposal that larger transactions are not supported. We put all attesters for that slot into groups of size 2 * T, with k = attesters_per_slot / (2 * T) groups.

Each attester is chosen to be the j’th attester of the i’th group. They identify the highest-priority-fee-paying valid transaction which was published before the slot N block, and where hash(seed + tx) is between 2**256 / k * i and 2**256 / k * (i+1). They erasure-code that transaction to 2T bits, and publish the j’th bit of the erasure encoding as part of their attestation.

When those attestations are included in the next block, an algorithm such as Berlekamp-Welch is used to try to extract the transaction from the provided attester bits.

attester_inclusion_list.drawio
attester_inclusion_list.drawio891×351 42.7 KB

The Reed-Solomon decoding will fail in two cases:

  1. If too many attesters are dishonest
  2. If attesters have different views about whether a particular transaction was published before or after the block, and so they are split between providing bits for two or more different transactions.

Note that in case (2), if the transactions are sufficiently small, advanced list decoding algorithms may nevertheless be able to recover several or all of the transactions!

The next block proposer will be able to see which transactions the attestations imply, and so they will be able to block transactions from the list by selectively failing to include attestations. This is an unavoidable limitation of the scheme, though it can be mitigated by having a fork choice rule discount blocks that fail to include enough attestations.

Additionally, the mechanism can be modified so that if a transaction has not been included for 2+ slots, all attesters (or a large fraction thereof) attempt to include it, and so any block that fails to include the transaction would lose the fork choice. One simple way to do this is to score transactions not by priority_fee, but by priority_fee * time_seen, and at the same time have a rule that a transaction that has been seen for k slots is a candidate not just for attester group i, but also for attester group i...i+k-1 (wrapping around if needed).

16 Likes
2

There’s one thing that itches me and it’s that the inclusion of this changes the attestation data, and therefore makes aggregating these attestations more complicated, to the point that it may affect how many attestations can be packed in the block. Just a tiny detail in the overall complexity of the protocol, but one nonetheless.

1 Like
3

One concern is how much additional latency this adds to the current critical path. With timing constraints, each node already has less than 1 second to process a block.

As a proposer, I have to manually parse the attestations to get the transactions. How does this work with MEV-Boost and builders? Will proposer be forced to use local blocks? or could there be incentive misalignment.

As a node runner, parsing through attestations to get the transactions and penalizing a censoring block using consensus rewards and penalties is a cross-layer action, takes longer, and will require additional engine API calls to accomplish this.

1 Like
4

If it’s one bit, it would only increase the total number of Attestation objects (and hence the number of pairings needed to verify) by 2x.

As a proposer, I have to manually parse the attestations to get the transactions.

These problems can be made pretty trivial if you make the attestations of slot N (which are included in slot N+1) define the inclusion list for slot N+2, so computing the inclusion list would be a pure function of the slot N+1 block. That’s the way I was thinking about it, I didn’t even think about making the inclusion list immediately binding on slot N+1. I suppose you could try to make that happen though! Though probably best to only do that after/if doing something like execution tickets, so we can count on execution proposers to be more sophisticated.

3 Likes
5

very interesting proposal!

a small typo: They erasure-code that transaction to 2k 2T bits.

1 Like
6

Interesting proposal. Would be great if we could rely on attesters instead of a single proposer.

Clarification questions:

  1. Do I understand correctly, that the size of the inclusion list is 1 for each slot?
  2. Why does it have to be the actual transaction and not just the sender, like in EIP-7547?

Observations:

When we make it binding, attesters will have to determine whether an excluded transaction was still valid at the beginning of the block, so they only vote against a block if it excluded a valid transaction that appeared in an inclusion list. With EOA it’ll be a simple static check but with AA it’ll require an eth_call.

Since the size of the inclusion list is small, would it be possible to cheaply circumvent inclusion lists by ensuring that the highest-priority-fee transaction at any given time is valid in the current block but invalid in the next one, so actual censored transactions never get listed?

With EOA it wouldn’t be free but can still be cheaper than paying the highest priority fee: propagate a high-fee transaction shortly before the cutoff time, but prepend with an earlier cheaper transaction, to be included in slot N. The cheaper transaction drains the EOA and invalidates the high-fee transaction.

With AA it may become free: shortly before cutoff, propagate a high-fee AA transaction that is valid in the current block but not in the next one. This could be mitigated by only listing transactions that follow the ERC-7562 rules, but requiring attesters to trace validations will increase validator hardware requirements.

I think this highlights a general downside of shifting the burden of inclusion lists to attesters (if we want it to support AA). The need to simulate validation, whether during inclusion list creation or during its enforcement, increases the validation cost.

5 Likes
7

In my understanding no, the size of the inclusion list is not necessarily 1 for each slot. The inclusion list size depends on the number of transactions that the attesters are able to encode and contribute to.

  1. Group Formation: The attesters for a slot are divided into groups, with each group being responsible for a portion of the transactions. The number of groups, k , is determined by k = attesters_per_slot / 2T.

  2. Transaction Selection: Each attester in a group identifies the highest-priority-fee-paying valid transaction for inclusion. The transaction selection is based on the seed and the hash range allocated to the group.

8

how would time_seen be calculated? Would it be based on a timestamp, block_number, or slot?