Fast (and Slow) L2→L1 Withdrawals

Layer 2
1

Co-authored by @The-CTra1n , @linoscope , @AnshuJalan and @smartprogrammer , all Nethermind. Thanks to @Brecht and Daniel Wang from Taiko for their feedback on this solution. Feedback is not necessarily an endorsement.

Summary

We introduce a new fast path for L2 withdrawals to L1 within the same L1 slot, enabled by solvers. To mitigate risks for solvers and maximize participation, solvers can observe preconfirmed L2 batches containing fast withdrawal requests and condition solutions for these requests on the batch containing the requests being successfully proposed to L1. This ensures no risk for solvers beyond the need to wait for the L2 state root containing the request to be proven on L1 to receive payment for facilitating the withdrawal.

Overview

This post introduces a protocol which we describe as Fast & Slow (FnS) withdrawals to enable rollup users to atomically withdraw tokens from L2 to L1. When we say atomically withdraw, we mean that the first time the L2 withdrawal transaction appears on L1, tokens can be made available for the L1 user in the same slot without introducing reorg risk to the L2 bridge. This is achieved through solvers who facilitate these atomic withdrawals.

Any L1 user can act as a solver. Prospective solvers observe L2 withdrawal requests on the L2 and solve the request on behalf of the L2 users on L1. This repurposes the entire L1 network as a network of solvers for fast L2 withdrawals. Leveraging that rollups post their transaction batches to the L1, FnS allows solvers to condition their withdrawal solutions on the sequence in which the L2 withdrawal exists. This allows the L1 solver to guarantee that the tokens being withdrawn by the L2 user will be made available to the solver when the state root containing the withdrawal request is proved on L1.

When the state root containing a request is proven on L1, the L2 tokens requested for withdrawal become available on L1. This is the “slow withdrawal”, which always happens. The solver of a request gains unique access to the slow withdrawal tokens corresponding to the request. As such, L1 solvers must wait some time before the L2 tokens become available on L1. As mentioned though, opting in to a fast FnS withdrawal is fully optional for solvers with no token lock-up for solvers except when they must wait for a slow withdrawal after providing a valid solution. Therefore, it is up to the L2 user to provide a fee covering:

  • the cost of waiting to receive the L2 tokens on L1
  • the L1 fees for submitting the solution and collecting the slow withdrawal tokens from the bridge.

How does it work?

In the following, we capitalize the Request, the Solution of the Request, the Users submitting the Request, and the Solvers providing the Solution, to ensure the objects are clearly differentiated from the verbs.

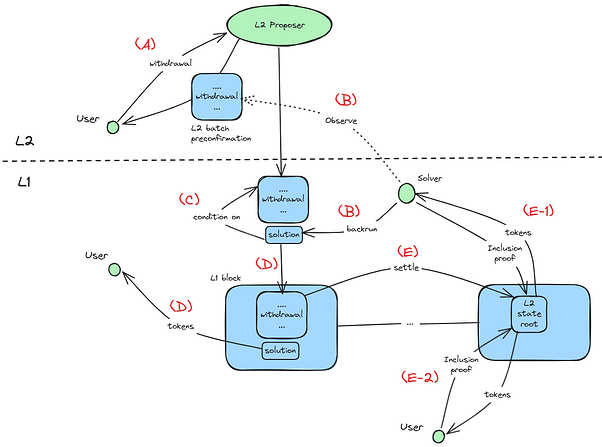
The diagram below illustrates how the fast path withdrawal facilitated by Solvers works:

1188×883 102 KB

  • (A) L2 Users wanting fast withdrawals send a Request to the L2 FnS contract, including the tokens the User wishes to withdraw and the L1 address to which the tokens should be sent.
  • (B) L1 Solvers (being a Solver is permissionless with no registration requirement) observing the FnS Request in an L2 batch through preconfirmations (or L1 mempool) can attempt to back-run the L2 batch with a Solution to satisfy the withdrawal Request. Solutions send the specified tokens to the specified destination address.
  • (C) Solutions can be conditioned on the L2 batch containing the Request, ensuring no reorg risk for Solvers who execute the L2 block: if the L2 block is recorded, the Solution doesn’t execute.
  • (D) At any time before a proven L2 state root containing the Request is provided to L1, a fast withdrawal via a Solution can take place.
  • (E) After a proven state root containing the Request is executed on L1, the slow withdrawal path is triggered. At that point, the L2 tokens in the FnS contract are available for withdrawal from the L1 FnS contract.
    • (E-1) If a valid Solution was provided for a valid Request (validity checked in state root proof), the Solver who submitted the Solution (only one Solution per Request gets accepted on L1) can withdraw the tokens from the L1 FnS contract.
    • (E-2) Otherwise, the User can withdraw their tokens from the L1 FnS contract.

Technical Specification

This section specifies the algorithm for FnS withdrawals.

Glossary of Smart Contracts and Transactions Used

We introduce the following terms, concepts, data structures, and smart contracts.

  • L1 rollup contract. The smart contract on L1 where the rollup/L2 state transitions are recorded and proven.
  • L2 transaction batch. The data structure through which L2 transactions are posted to the L1 smart contract representing the L2. Each L2 transaction batch can be accompanied by a signature verifying the signer proposed the batch.
  • L2 proposer. With respect to a given L2 batch of transactions, the entity with permission to post the batch to the L1 rollup contract. This proposer role can either be:
    • permissioned. In the case of centralized sequencer, or preconfirmer, the L2 proposer is the respective centralized sequencer or preconfirmer.
    • permissionless. Anyone can sign for and submit the batch.
  • L2 Withdrawal Request: An L2 transaction from an L2 user specifying
    • Request ID. A unique identifier for each Request which is a collision resistant commitment to the other variables in this Request, e.g. a hash of the encodings of these variables.
    • L2 input tokens. Sent to by the user (token address and amount)
    • Output Condition 1. L1 output tokens (token address and amount)
    • Output Condition 2. L1 output address. Address where the L1 output tokens must be received.
    • Nonce. Nonce used to generate a unique Request ID.
  • Solver: Entities that “solve” user Requests by satisfying the L1 output conditions of Requests.
  • Solution: An L1 transaction from a Solver which satisfies the L1 output conditions of a Request. Although Solvers can solve Requests by any means producing the output conditions, only one Solution is allowed per Request ID. Solutions have the following inputs:
    • ( L2 input tokens, Output Condition 1, Output Condition 2, Nonce)
    • Request ID. Must correspond to the commitment function output results from the previous variables in the Solution. Note, the L1 smart contract does not need to read L2 state to match Solution “Request IDs” with actual Request IDs. This is the job of the Solver.
    • Chained L2 batch commitment. A commitment of (previous chained L2 transaction batch commitment, current L2 transaction batch commitment) pair. Needed to prevent double spends of Request input tokens.
    • L1 Solver output address. Address where the L2 input tokens of Request ID are to be sent if Request ID was correctly solved.
    • Calldata (where the actual solving is done, can be any instruction e.g. send the tokens to the L1 Solver contract, which then sends tokens according to the output conditions).
  • L1 Solver Contract: An L1 smart contract which takes as input Solutions. For each solution, it should record the Request ID to prevent double solving (a bad thing). For each Solution, the L1 Solver Contract must verify that the L2 output conditions specified in the Solution were satisfied.
  • (L1-L2) Bridge Contract: A contract that lives on L1. L2 tokens sent to specific burn contracts on L2 can be withdrawn on L1 from the Bridge contract when a proven L2 state root is provided to the bridge which contains those token burns on L2. For this document, we assume this is the only way to withdraw tokens from L2 to L1.
  • L2 Solver Contract: An L2 smart contract where Requests are sent. Tokens sent to the L2 Solver Contract are burned and signalled for withdrawal on L1 from the Bridge Contract.
  • L1 Solver Withdrawal Transaction: Contains:
    • L2 State Root ID: ID of a proven L2 state root posted to L1.
    • Request ID.
    • Merkle Proof: Proof of existence of Request ID in the state root corresponding to L2 State Root ID.
  • L1 User Withdrawal Transaction: Contains:
    • L2 State Root ID: ID of a proven L2 state root posted to L1.
    • A full L2 Withdrawal Request transaction: (L2 input tokens, L1 output token address, L1 output address, Nonce, Request ID)
    • Merkle Proof: Proof of existence of Request ID in the state root corresponding to L2 State Root ID.

Protocol Description

We will now step through the protocol.

  1. L2 User submits a valid Request to L2 Solver Contract.
  2. L2 proposer includes the Request in an L2 transaction batch, signs the batch.
  3. Solver reacts to Request in a valid signed batch:
    1. Observe a valid Request in a signed batch.
    2. Construct a Solution to the Request (how to satisfy Request output conditions), according to the format specified in the Glossary.
    3. Either:
      1. Solver creates a bundle of L1 transactions, with the first transaction being the L2 batch containing the Request, and the second being the Solution to the Request
      2. Solver submits the Solution to a third party, e.g. the L2 proposer, another Solver solving another Request(s), to be bundled together with the L2 batch, with this bundle posted to L1.
  4. L2 transaction batch is received on L1 to the L1 rollup contract.
    1. If the L2 proposer is permissioned, verify the accompanying signature was from the L2 proposer (NOT the same as verifying msg.sender).
  5. Solution received on L1 to L1 Solver contract. For given Solution of the form,
    (L2 input tokens,
    L1 output token address,
    L1 output address,
    Nonce,
    Request ID,
    Chained L2 batch commitment,
    L2 solver output address,
    Calldata     ),
    do the following, or revert:
    1. Verify no other Solution has been submitted corresponding to Request ID.
    2. Verify Request ID matches the commitment of (L2 input tokens, L1 output token address, L1 output address, Nonce).
    3. Verify there exists L2 batches corresponding to chained L2 batch commitment.
    4. Execute Calldata.
    5. Verify Request’s Output Conditions were satisfied.
  6. State Root containing Request is proven and submitted with proof to the L1 rollup contract.
  7. Solver of a Request submits an L1 Solver Withdrawal Transaction to the Bridge Contract. Complete all of the following, or revert:
    1. Verify Withdrawal’s Merkle Proof is valid.
    2. Verify Solver address matches the L1 Solver Output Address corresponding to the Solution which corresponds to Request ID of the L1 Solver Withdrawal Transaction.
    3. Send L2 Input Tokens corresponding of the Request corresponding to Request ID to the Solver.
  8. User who submitted a Request sends an L1 User Withdrawal Transaction to the Bridge Contract. Complete all of the following, or revert:
    1. Verify Withdrawal’s Merkle Proof is valid.
    2. Verify no Solution exists corresponding to Request ID.
    3. Send L2 Input Tokens of the Request corresponding to the User*.*

Comparisons

Across

The proposed solution can be viewed as a variant of an intent-based solver solution, similar to protocols like Across. However, a key distinction lies in enabling Solvers to condition their solutions on batches from the source chain, thereby eliminating the reorg risk of the source chain. This is possible because the source chain is a rollup, while the destination is the L1 it settles to—i.e., the source chain batch is submitted directly to the destination chain.

Aggregated Settlement

Aggregated settlement enables synchronous composability between L2s by conditioning one rollup’s settlement on the state of others. This allows a rollup to import messages from another, execute L2 blocks based on them, and later revert execution if the messages are found invalid by verifying the other rollup’s state root at the shared settlement time. This protocol effectively enables synchronous composability between L2s by utilizing the fact that the L2s share a settlement layer. However, aggregated solutions do not address L2→L1 composability, as the L1 cannot reorg based on the settled state of an L2.

3 Likes
2

Loving it.

Simplifying, FnS protocol can be thought of as L2->L1-only intent-based bridging order book, right? I think you can continue this logic further by opening a way for L1-based users to bridge to the L2s with negative fees by closing these orders, instead of using the native bridge.

For example, Alice wants to unbridge 1 ETH to the L1 and is willing to pay 0.1% for this unbridging to be fast. Bob wants to bridge 2 ETH and has two choices:

  • Use the native L2 bridge and get the funds 1:1 → 2 ETH
  • Close Alice’s 0.999 ETH order in exchange for 1 L2-ETH and bridge the rest, 1.001 ETH, via the native bridge → 2.001 ETH

Not only this incentivizes moving to the L2s, but also helps to achieve equilibrium in bridging between L1 and L2s. Today’s bridges usually take a fee both ways—for example, in Across. it’s 0.01% for ->L2 transfers and up to 0.1% for ->L1 transfers. With such order book bridging, it could be, say, 0.1% to L1 and -0.1% to L2.

2 Likes
3

Didn’t quite follow - How does it solve re-orgs risk of the L2 bridge?

It’s using the state root of the L2 as the state of truth but in optimistic rollups, the state root can change after posting due to the 7 day delay?

2 Likes
4

The solutions are not conditioned on the L2 state root but rather on the L2 batch. Conditioning the solution on the batch protects solvers from reorg risks, such as:

  • The L2 proposer preconfirms an L2 batch but eventually submits a different batch to L1 or fails to submit their batch due to a liveness failure.
  • An L1 reorg causes the corresponding L2 batch to be reorged out of the chain.
2 Likes
5

Nice post.

Does the reorg risk of the solver include the rollback of rollup state by the fraud challenge during the challenge window?

1 Like
6

Yes, it does. However, given the Solver can condition on the batch in which the request is positioned, the Solver can remove this rollback risk by ensuring the batch is valid and provable. If not, the Solver has no obligation to provide a Solution.

7

So the solver knows the L2 batch commitment ahead-of-time because this was preconfed. I understand that they avoid reorg risk because they condition their Solution on the L2 batch commitment already being on the L1 at the time their Solution is executed (i.e., solver backruns).

Maybe this is just a tech implementation detail but how does the solver know if the Request contained in the L2 batch is valid? Since the preconf is just about batch inclusion, without verifying a proof or re-executing the L2 state, a solver could (at their peril) solve the fast path and then be unable to claim in the slow path because the Request is invalid (i.e., the solvers “condition” would be satisfied but they could be rugged by the preconfer).

8

Yes, exactly!

Yeah, just examining the request in the batch isn’t enough for the solver, as the request could be reverted. Hence the solver would want to execute the batch locally to confirm the request’s validity.

9

Thanks!
Again maybe this is more in the engineering weeds but does this imply that the batches would need to be propagated to all the potential solvers, JIT? By far the simplest implementation would be that the preconfer is the solver but this could add unwanted capital requirements.

10

Yes, we assume there is a preconfirmation protocol that preconfirmes and publishes these batches. The solver relies on preconfer to publish the batches so they can craft solutions based on it, but the conditioning on the batch protects such solvers from preconfer equivocation or liveness fault.

Yeah, the preconfer would be a natural fit for being solvers, and may be the dominating solver in practice. But that does, as you mention, bring unwanted capital requirements to the preconfer. So the proposed solution here lets the preconfer “outsource” the solutions to external solvers while protecting the solvers from preconfer equivocation.

1 Like
11

Nice proposal.

Would be useful to explicitly list the assumptions about the participating rollup, including:

  1. Valid batches cannot be reverted (except by L1 reorgs),
  2. Batch validity (and provability) can be known to solvers immediately.