Summary
The challenge is collecting cryptographic signatures from nearly a million validators distributed globally across the network within 12 seconds, without needing high-bandwidth internet connections from any consensus nodes.
To address this, we are exploring alternative schemes to achieve single-slot finality while minimizing bandwidth usage. The aim is to reduce the time to reach finality significantly. The robustness and scalability of these approaches are being evaluated through simulations.
Motivation
In the current implementation of the Ethereum PoS consensus mechanism, blocks are deemed finalised only after 64-95 slots (1-2 epochs), which takes 15 minutes on average. Currently one has to wait this amount of time for the protocol to reach supermajority (i.e., 67%) agreement on state transitions over approximately 800\,000 validators,
-
without revealing the IP addresses of the validators,
-
limited bandwidth usage (say \sim8 GB per day),
-
has a succinct proof about the supermajority on the chain,
-
being resilient against malicious nodes.
In the protocol designed for collecting attestations in PoS Ethereum, called Casper, validators generate a BLS signature as the cryptographic proof of the attestation. In each slot, the validators are pseudo-randomly assigned to 64 committees. Each validator broadcasts its BLS signature among the corresponding committee members. This broadcast is implemented through a so-called publish-subscribe (pub-sub) service of libp2p. In each committee, 16 nodes are pseudo-randomly selected as aggregators. They listen to these channels and broadcast a signature aggregation message on some global channels. The signature aggregation message contains a bit-vector of equal size to the committee and a single BLS signature, the sum of the corresponding BLS signatures. From each committee, the best aggregation message is included in the chain.
Discussion on Casper
Hiding the IP addresses of the validators
To preserve the privacy of validators, their IP addresses are concealed using a DHT routing protocol of the P2P network. In gossip protocols, participating nodes forward messages without knowing the message’s original source. Additionally, this protocol incorporates message relaying for enhanced privacy and network efficiency.
Remark: Overall, hiding the IP addresses is not the primary goal of any DHT routing protocol. They are designed for peer-to-peer networks, eliminating the need for a centralized server. It scales well as the network grows, making it suitable for large distributed systems. Furthermore, it is considered fault tolerant, as DHT is designed to handle nodes joining and leaving the network frequently.
Limited bandwidth usage
In our measurements, a consensus client uses an average of 8GB per day to collect attestations, which we consider a reasonable upper bound in our system design. Technically, for each committee, a pub-sub service of libp2p is utilized. The consensus client broadcasts each BLS signature within the corresponding pub-sub channel, leading to high bandwidth consumption.
To reduce bandwidth, Casper divides time into epochs consisting of 32 slots, with each validator assigned to a single slot within each epoch. Consequently, only 25,000 validators participate in attestation during each slot, a fraction of the total 800,000 validators. While this method conserves significant bandwidth, it extends the time to achieve finality. Currently, Gasper takes between 64 and 95 slots (2-3 epochs) to finalize blocks.
Remark: The term ‘pub-sub’ in libp2p might be somewhat misleading as it operates more like topic channels where any node can initiate a broadcast, differing from typical pub-sub systems where publishers are distinct from subscribers and only the former can initiate broadcasts.
A succinct proof about the supermajority on the chain
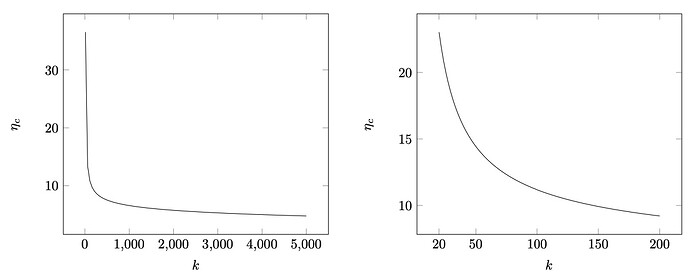
As a key performance indicator, we investigate the number of bits required to be included in the blockchain per validator, a metric we call chain cost per ID, denoted as \eta_{c}. Each validator, registered in the blockchain with a public key and a 32 Ether stake, can be identified by their ID, eliminating the need to use public keys directly. The cryptographic evidence for an attestation, digital signatures, are 256 bits in length. Notably, these signatures can be aggregated, allowing verification of the aggregated signature against public keys (or IDs) without needing each individual signature.
To estimate \eta_{c}, consider \mathcal{V}=800,000 validators. The bitfield, representing validator participation, is \frac{\mathcal{V}}{32 \cdot 64} \approx 390 bits long. Appending this with the 256-bit BLS signature, the chain cost per ID is approximately \frac{390+256}{390} \approx 2 bits. This is quite efficient, yet the ideal scenario would be where all 800\,000 validators sign the block, requiring only 256 bytes for proof. In such a case, the chain cost per ID could be reduced to \eta=\frac{256}{800000} \approx 10^{-3} bits.
Being resilient against malicious nodes
In Casper, 16 aggregator nodes are randomly selected for each committee. If an attacker were to successfully suppress every aggregator node in a given committee, it would result in the loss of all signatures gathered by that committee. Given that there are 64 committees, the impact of such an attack is negligible in the consensus process. In our system design, we follow a similar approach to redundancy.
Note that the messages are of a fixed size, and the signatures are verified prior to aggregation to prevent manipulations by malicious nodes.
Alternative Signature Aggregation Scheme
Our high-level idea is that using more flexible data structures is advantageous for rapid data collection, as it minimizes the need for extensive coordination.
In the current implementation, validators use a data structure comprising bit-vectors for both inter-node communication and for inclusion in the blockchain, but this approach has limitations. For communication, the requirement that aggregated signatures be disjoint for further aggregation can be restrictive. Gasper tackles the issue of disjointness in signature aggregation by allocating each validator to one of the 64 committees. This allocation occurs pseudo-randomly at the start of each epoch, an approach vital for maintaining validator privacy.
When it comes to incorporating bit-vectors into the blockchain, they become less efficient if most bits are set to 1, which happens very frequently with block attestations. In these instances, encoding the positions of the zero bits is a more efficient approach.
We investigate flexible aggregation frameworks wherein a single signature can appear multiple times in an aggregated signature. This feature becomes advantageous in scenarios involving multi-level aggregation, where combining two previously aggregated signatures with a common validator is required. In such instances, accurately recording the multiplicity of each validator’s signature is important.
In this context, the coefficient is ideally one or a small number; however, it has the potential to be large without explicit upper limits.
Data structure for validator IDs and coefficients
The goal is to effectively store the IDs and coefficients of the validators who contribute to an aggregated signature. Validators are identified on-chain by IDs in the range [0,\mathcal{V}], with \mathcal{V}\leq 2^{22} as per Ethereum 2.0, and it is expected to increase to 1-2 million in the near future.
Each validator is marked by a distinct ID and a coefficient, usually one, but without a fixed upper limit. Our process should provide convenient ways to merge two of instances of such structures. This merging entails calculating the union of the two sets of IDs, along with their corresponding aggregated signatures.
In a nutshell, the data proposed structure is the following: we maintain a sorted list of IDs, recording the non-negative differences between successive IDs. A zero difference indicates redundant signatures. These differences are stored using prefix codes that are variable length codes. We use Huffman codes, which attain Shannon’s compression limit if the frequency distribution of the differences is predetermined. The sorted list allows for efficient merging.
To illustrate the proposed data structure, let us consider the following example. Suppose we have the following set of IDs:
| ID | 10 | 8 | 2 | 15 | 18 |
|---|---|---|---|---|---|
| Coefficient: | 1 | 2 | 1 | 1 | 1 |
First, we organize the IDs in ascending order and replicate each ID according to its coefficient, resulting in:
2, 8,8,10,15, 18 \enspace .
In our data structure, we record the non-negative differences between successive IDs, with the first element being the ID itself. This yields:
2, 6, 0, 2, 2, 5, 3 \enspace .
The list, composed of integers in the range [0,2^{22}], can be stored more efficiently using Huffman coding. In binary integer coding, each integer would require 22 bits, but Huffman coding optimizes this by assigning variable-length codes based on frequency. Let k dente the number of unique IDs in the list. With an average integer value expected to be less than \frac{\mathcal{V}}{k}, Huffman coding would represent these integers in fewer than 22 bits on average. This efficiency is achieved by using a prefix code that assigns shorter codes to more frequent integers and longer codes to less frequent ones. The frequency we estimate using a geometric distribution based on the mean \frac{\mathcal{V}}{k}. For instance, with \mathcal{V}=20 and k=5, the Huffman codes for integers would be:
| number | binary code |
|---|---|
| 0 | 11 |
| 1 | 01 |
| 2 | 101 |
| 3 | 001 |
| 4 | 1001 |
| 5 | 0001 |
| 6 | 10001 |
| 7 | 00001 |
| 8 | 100001 |
| 9 | 000001 |
| 10 | 1000001 |
| 11 | 0000001 |
| 12 | 10000001 |
| 13 | 00000001 |
| 14 | 100000001 |
| 15 | 000000001 |
| 16 | 000000000 |
| 17 | 1000000000 |
| 18 | 10000000010 |
| 19 | 100000000111 |
| 20 | 100000000110 |
The bit encoding begins with the binary representation of k, the number of unique IDs. We may assume there are maximum of k \leq 2^{20} IDs due to IP packet size limits. For k=5, its 20-bit-long binary representation is 0...0101. In your example, the encoding sequence is
0\dots0101 \quad 101 \quad 10001 \quad 11 \quad 101 \quad 101 \quad 0001 \quad 001
which totals to 20+3+5+2+3+3+4+3=43 bits. This results in an average of 8.6 bits per unique ID.
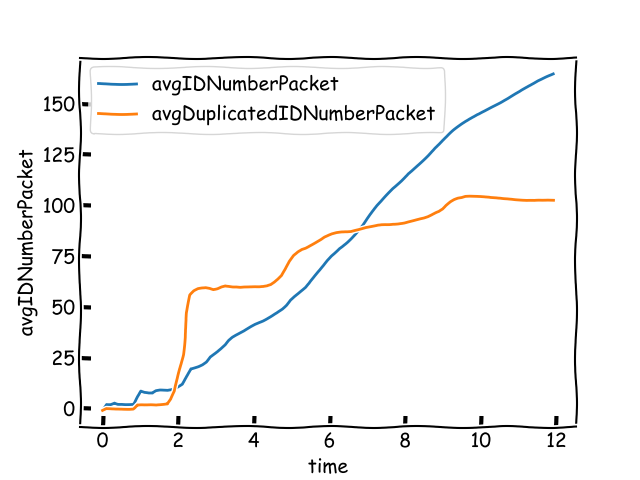
In our simulation involving 800\,000 validator IDs, we observed an average storage requirement of \sim10 bits per ID. This method exhibits approximately 50% space savings when compared to the straightforward approach of storing validator IDs using a 20-bit binary representation.
Message for disseminating aggregated signatures
We can now detail a typical message used for spreading aggregated signatures. This message incorporates the data structure mentioned earlier, along with an extra 256-bit BLS signature. Two aggregated signature messages can be merged efficiently: the union of two ID lists is accomplished in linear time using the merge algorithm, which operates on IDs sorted in ascending order. Additionally, the process of aggregating BLS signatures is expedient, as it simply involves adding two elliptic curve points.
Verifying the validity of these messages is a process that can be completed in just a few milliseconds.
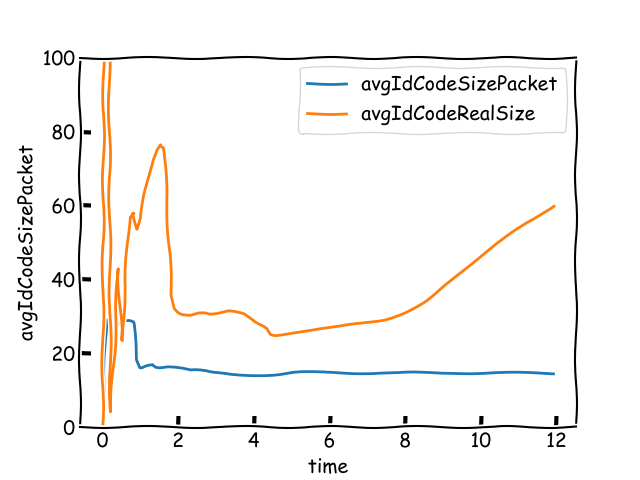
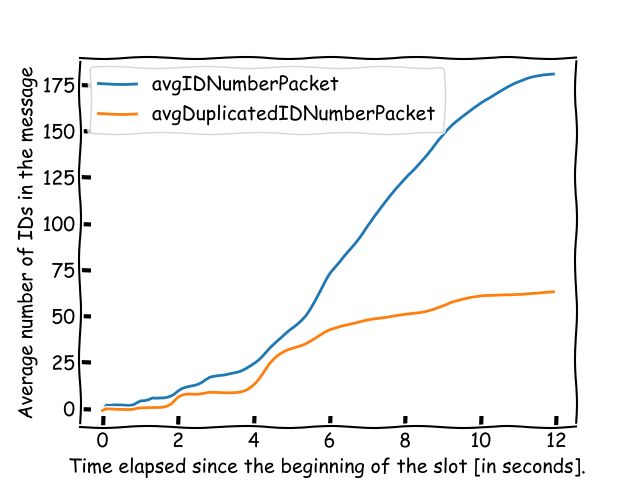
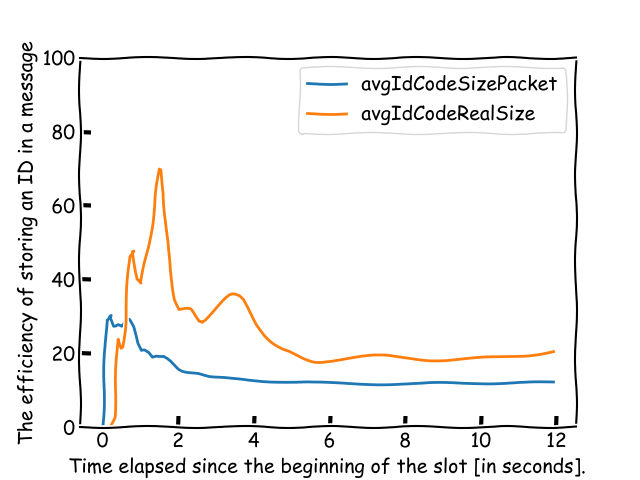
For the previous example, the chain cost per ID of such a message would be \eta_c=\frac{43+256}{5}\simeq 60 bits. The chain cost per ID decreases if there are more unique IDs included in the message. Nevertheless, each duplicated ID requires only 2 extra bits (i.e., the binary code 11). More unique IDs result in a smaller chain cost per ID because of two reasons. First, the fixed-size BLS signature is divided by more IDs, and second, the mean value of the integers stored in the data structure is smaller.
Using Huffman coding with a geometric distribution allows us to represent the impact of the encoding with a closed formula. The data structure encodes the differences between ascending IDs, summing to less than \mathcal{V}. Consequently, the average value of these IDs is \frac{\mathcal{V}}{k}. In a geometric distribution, the probability of the x-th value is given by p(1-p)^x, where p is the success probability. For a mean of \frac{\mathcal{V}}{k}, we get p=\frac{1}{\frac{\mathcal{V}}{k}+1}. The encoding length for zero, which indicates a duplicate ID, is \log_2(p), while for an integer x, it is \log_2(p(1-p)^x). The average length for unique IDs, or the Shannon Entropy, is calculated as \frac{-(1-p)\log_2(1-p)-p\log(p)}{p} \enspace .
In summary messages containing fewer than 20 unique IDs exhibit significant inefficiency (\eta_c>20). Conversely, the curve’s slope tends to flatten for messages incorporating more than 200 unique IDs (\eta_c<10).
An ad-hoc signature collection approach
Every node in the network tracks the signatures it receives. Recall that these messages include the IDs of the validators along with their corresponding aggregated signatures. Each node maintains a single aggregated signature formed by merging the recently received aggregated signature messages. Time-to-time, each node sends these signatures to this aggregated signature message to all of the neighbors, except those from whom it received the message.
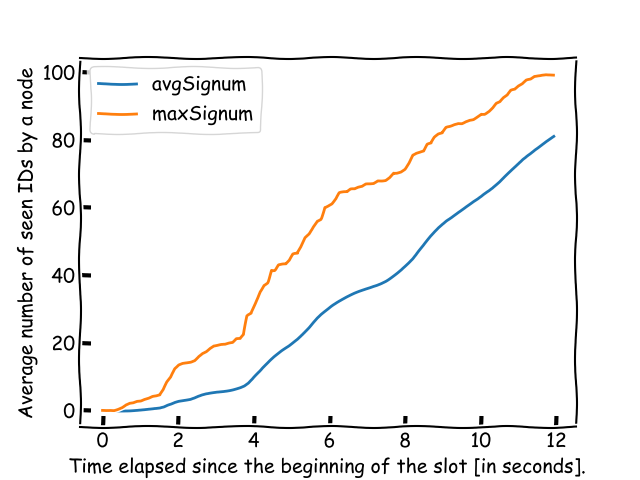
A node is considered to have seen a signature if it receives a valid message containing an aggregated signature with the corresponding ID. This means the node is aware of the signature’s existence, even if it doesn’t know the signature itself.
When a node gets an aggregated signature message, it verifies the BLS signature and counts the number of new IDs. Messages with no new IDs are dropped. the following processing is applied to the message.
If a message’s subset of IDs has been received before and can be inferred, the node modifies the message by subtracting the BLS signature and removing these IDs from the list. This step avoids resending known signatures to neighbors, conserving bandwidth.
The node also checks if it can compute individual BLS signatures for the received message IDs using previous messages. This is done via linear algebra (running Gauss elimination). For example, if a node first receives a message with IDs 1 and 2, and then one with IDs 1, 2, 3, by subtracting the second message, it can isolate the signature for the validator with ID 3. In this case we say the node knows ID 3, and have seen IDs 1 and 2.
The node implements heuristics to reduce ID redundancy and counter potential attacks. For each packet, it calculates a usefulness metric, defined as the message’s bit-size divided by the count of new IDs. If this usefulness metric is excessively low, the message is excluded from the merging process.
The node typically waits for a brief period, such as 100 milliseconds, to collect additional messages for merging before transmitting them.
Virtual IDs
The debate to raise the required Ether stake for becoming a validator from 32 ETH to 2048 ETH is ongoing, see. As an alternative, we are exploring the use of virtual IDs. A virtual ID, registered on-chain, represents a group of validator IDs. These IDs can be encoded using the method we previously outlined. By registering one or several attached validators under a virtual ID, a node can conserve bandwidth, benefiting not just itself but also the entire network.
Evaluation
Simulating novel algorithms on Ethereum’s mainnet with a sheer number of validators isn’t feasible. Therefore, we developed a discrete event simulator in C++ that uses real network topology to emulate block proposal, signature collection, and aggregation events. Since the exact number of validators per consensus client is obscured, we infer it from the count of attestation pub-sub channels a node subscribes to.
Using the Nebula crawler, we mapped the libp2p topology with 9\,294 nodes and 934\,266 links.
We assigned \mathcal{V}=800\,000 validators to nodes based on their attestation pub-sub channel subscriptions. Nodes with 64 subscriptions are presumed to have a high number of validators, capped at 256. Validator distribution across these nodes follows an exponential model.
To estimate the one-way delay for each link, we localize nodes based on their IP addresses and calculate the geographical distance between them. We assume the cable length connecting two nodes is twice their physical distance. The data transmission occurs at the speed of light. Additionally, we factor in a constant additive delay of 10 milliseconds for each link to account for other latencies. For further details and discussion on this topic, please refer to the appendix.
The simulation begins by randomly selecting a network node to broadcast the proposed block, initiating the signature aggregation process. This block is then transmitted to the node’s peers, with arrival times based on the Round-Trip Time (RTT) data gathered from our June 2023 network measurements. We assume each node can validate the block and produce a valid BLS signature within 1 millisecond. The signature collection phase then proceeds using our heuristic approach, eliminating the need for gossipsub subscriptions and discovery processes. We also assume that peer connections remain stable, with no disconnections occurring during the collection.
Simulation 1
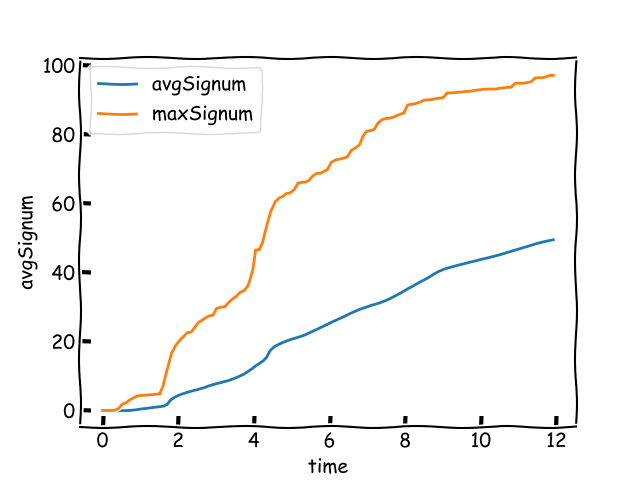
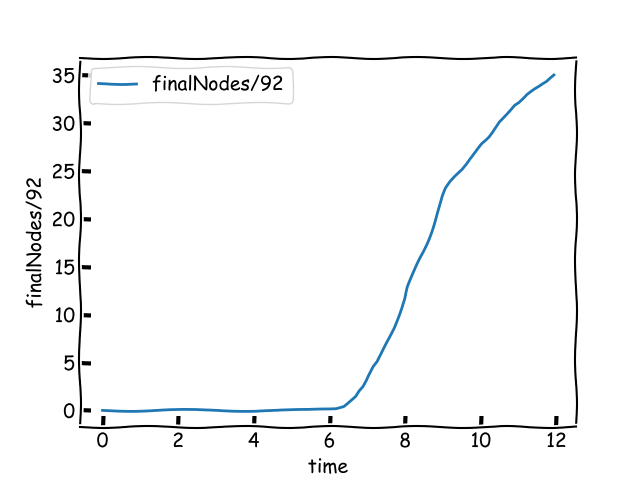
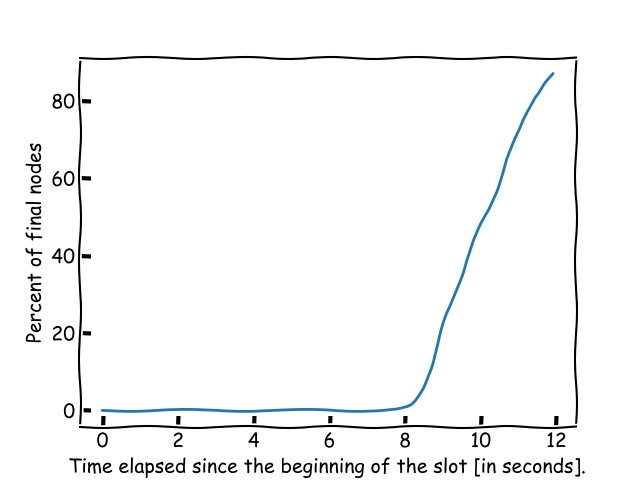
The 95\% of the nodes use virtual IDs among the ones with at least 10 validators. That is 1\,352 virtual IDs in total. There are 7\,833 nodes with validators among 9\,294 nodes.
Most nodes received the block before 0.49 seconds. The first node reached finality at 5.5 seconds of the start of the block. The estimated bandwidth requirement per day is 10.9 GBytes. 35% of the nodes reached finality by the end of slot.