Background
Hi all, we have been studying Proof of Solvency (PoSol) since last month for our centralized exchange (CEX), relying on ZK-SNARKs but not third party auditing. Inspired by the nice post written by @vbuterin, we decided to refind it and draft a tentative instance of a customized IOP implementation of PoSol mentioned in the post.
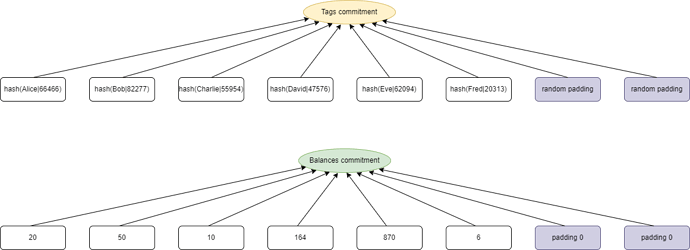
hash(username, salt) is an exclusive tag to each user, construct a vector filled with all users’ tags and commit it, which means each user’s position slot has been confirmed. Similarly we construct a balances vector, where all elements are listed in the order of tag vector. (We think saperately committing is better than combining them into a single vector, as CEXs usually own millions of even billions of users, forcing us to minimize the vector’s length to fit size of FFT domain).
After CEX has submitted a validated total balance with Tag Commitment and Balance Commitment on blockchain, user can calculate and verify his own balance by himself under a KZG polynomial commitment scheme. with given position value, salt, tag proof and balance proof from CEX.
Circuit
Consider \mathbb{F} a finite field of prime order. For a given integer n (n should be greater than number of users), denote by N=\left \{0,1,...,n-1 \right \}. Define the multiplicative subgroup H=\left \{ 1,\omega ,\omega^2,...,\omega^{n-1} \right \} as the subgroup containing the n roots of unity in \mathbb{F}, where \omega is a n-th root of unity and a generator of H.
Define T={\left \{ t_0,t_1,t_2,...,t_{n-1} \right \}} as users’ tags vector of size n. (use zeros to take up remaining slots). Define B=\left \{b_0,b_1,b_2,...,b_{n-1}\right \} as users’ balances vector of size n. (use zeros to take up remaining slots).
Consider S=\left \{s_0,s_1,s_2,...,s_{n-1}\right \} as an auxiliary vector. Shift left one unit for each element of S in loop, we get S'=\left \{s_1,s_2,...,s_{n-1},s_0 \right \}. Define a constant vector L_0=\left \{ 1,0,...,0 \right \}. Note that if we force S'-S=B-m\cdot L_0 at the vector level, whatever elements in S are, it must satisfy m=\sum_{i=0}^{n-1}b_i, which is the balance sum that we want to declare.
Now we can construct an instance S=\left \{\sum_{i=0}^{n-1}b_i,b_0,b_0+b_1,...,\sum_{i=0}^{n-2}b_i\right \}, which satisfys S'-S=B-m\cdot L_0. That’s an entrypoint for us to build a PoSol proving scheme.
Polynomial Format
Denote by f(X)\in\mathbb{F}_{\le l}[X] that degree of polynomial f(X) over \mathbb{F} is no more than l. Define the i-th Lagrange polynomial L_i(X)\in\mathbb{F}_{\le n}[X], where i \in N. Define vanishing polynomial Z_H(X)=\prod_{i=0}^{n-1}(X-\omega^i)=X^n-1.
Transform T, B and S to polynomials by inverse FFT over H, we got T(X), B(X) and S(X), and S' corresponds to S(\omega X). Moreover, consider the first Lagrange polynomial L_0(X), which has the property of taking value 1 at x=1 while taking value 0 at any other elements in H. According to the above discussion, we have a polynomial equation at all elements in H:
We can write this more reasonably as a polynomial division format:
Range Constraint
The CEX could set remaining elements in B negtive (because no one can check these special padding balances) to reduce the declared balance sum m and be evil. That’s why vitalik says there needs a non-negative proof. Hereby we give a brief introduction to an elegant solution for continuous ranges proposed in Plookup protocol.
Define t=\left\{0,1,2,...,n-1\right\} as a lookup-table vector. Suppose each balance is less than n (If balance exceeds n, we can split into multiple n-decimal representations for repeating), then we just need to prove each element in B can be found in t.
Let V=\left \{v_0,v_1,...,v_{2n-1} \right\} be the vector that combines (B, t) and sorted by t. Denote by h_1=\left \{v_0,v_1,...,v_{n-1}\right\} and h_2=\left \{v_n,v_{n+1},...,v_{2n-1}\right\}. h_1 and h_2 can be constrained as following:
-
Elements in both h_1 and h_2 must increase step by either 0 or 1.
-
The first value in h_1 must be 0.
-
The last value in h_1 must be n-1.
-
The first value in h_2 substract the last value in h_1 must be either 0 or 1.
Then we just need to prove all elements in B and t are completely as same as those in h_1 and h_2, while using a permutation constraint mentioned in Plookup.
Protocol
With the above preparation work, we describe a similar protocol based on KZG commitment referred to the Plonk protocol creation process.
Common Referenced String
Proving Process
We use transcript for obtaining random challenges via Fiat-Shamir. Initialize transcript with n.
Round 0
-
Compute tags polynomial commitment [T(X)]_1.
-
Compute balances sum of all users in field \mathbb{F}, denote by m \in \mathbb{F} as a public input. Append it into
transcript.
Round 1
-
Generate random blinding scalars a_0,a_1,...,a_4 \in \mathbb{F}.
-
Compute blinded balance representation polynomial B(X) \in \mathbb{F}_{\le n+1}[X], \ i<k:
- Compute blinded auxilary polynomial S(X) \in \mathbb{F}_{\le n+2}[X]:
- Compute [B(X)]_1 and [S(X)]_1. Append them into
transcript.
Round 2
- Generate random blinding scalars c_0,c_1,...,c_5 \in \mathbb{F}. Compute blinded polynomials h_1(X) \in \mathbb{F}_{\le n+2}[X], h_2(X) \in \mathbb{F}_{\le n+2}[X]:
- Compute h_1(X) and h_2(X). Append them into
transcript.
Round 3
- Compute the permutation challenge \gamma \in \mathbb{F}.
- Generate random blinding scalars d_0,d_1,d_2 \in \mathbb{F}. Compute permutation polynomial z(X) \in \mathbb{F}_{\le n+2}[X]:
- Compute [z(X)]_1. Append it into
transcript.
Round 4
- Compute the quotient challenge \delta \in \mathbb{F}.
- Combine all of the polynomial constrains and compute the quotient polynomial q(X) \in \mathbb{F}_{\le 2n+6}[X]:
- Split q(X) into 2 polynomials q_0'(X)\in \mathbb{F}_{\le n+2}[X], q_1'(X)\in \mathbb{F}_{\le n+3}[X], such that
- Generate random blinding scalars e_0 \in \mathbb{F}. Computed blinded polynomials q_0(X), q_1(X):
- Compute [q_0(X)]_1 and [q_1(X)]_1. Append them into
transcript.
Round 5
- Generate the evaluation challenge z \in \mathbb{F}.
- Compute the opening evaluations and append them into
transcript:
Round 6
- Generate opening challenge \eta \in \mathbb{F}.
- Compute linearization polynomial r(X)\in \mathbb{F}_{\le n+3}[X]:
- Compute the opening proof polynomial W_z(X)\in \mathbb{F}_{\le n+2}[X]
- Compute the opening proof polynomial W_{\omega z}(X)\in \mathbb{F}_{\le n+2}[X]
- Compute [W_z(X)]_1 and [W_{\omega z}(X)]_1.
Now we have the complete proof:
Send both the public input m and the proof \pi_{PoSol} to the verifier.
Verifying Process
Verify
-
Validate m and all elements in \pi_{PoSol} are valid.
-
Compute challenges \delta,\ z,\ \eta \in \mathbb{F} via
transcriptas in the prover’s algorithm description, with m and elements in \pi_{PoSol}. -
Compute the vanishing polynomial evaluation Z_H(z)=z^n-1.
-
Compute the first Lagrange polynomial evaluation L_0(z)=\frac{z^n - 1}{n(z - 1)}.
-
Compute the last Lagrange polynomial evaluation L_{n-1}(z)=\frac{\omega^{n-1}(z^n - 1)}{n(z - \omega^{n-1})}.
-
Compute the first evaluation p:
- Compute the first commitments combination [P]_1:
- Compute the second evaluation u:
- Compute the second commitments combination [U]_1:
- Verify KZG opening proof by pairing engine e([\bullet]_1,[\bullet]_2):
Remark
Confined to limitations of our understanding on cryptography and ZKSNARK, if there are any mistakens or defects, please point out or give us some suggestions.
If there are no bugs in the protocol, we will open source as soon as possible, thanks!