Shumo Chu, Sebastien La Duca, and Brandon Gomes (@bhgomes) (ordered Alphabetically)
Special thanks to Yi Sun on Proof-of-Asset discussion, and Dankrad Feist and Daniel Lubarov for helpful discussions on FRI
Problem Definition
Proof of Solvency (PoSol) answers a simple question:
Can we build cryptographic proofs to show that a Centralized Exchange (CEX) has enough reserves to back all user funds?
If you prove that customers’ deposits equal X (“proof of liabilities”), and prove ownership of the private keys of X coins (“proof of assets”), then you have a proof of solvency: you’ve proven the exchange has the funds to pay back all of its depositors.
So in very simple terms:
\text{Proof of Solvency}: \textsf{PA}\,\,(\text{Provable Assets}) - \textsf{PL}\,\,(\text{Provable Liabilities}) \ge 0
Proof of Assets
The simplest solution is just signing transactions over the owned addresses:
To prove that you hold X coins, you simply move X coins around at some pre-agreed time or in a transaction where the data field contains the words “these funds belong to Binance”. To avoid paying transaction fees, you could sign an off-chain message instead; both Bitcoin and Ethereum have standards for off-chain signed messages.
To protect privacy and avoid revealing the entire set of the CEX’s addresses, a zero-knowlege proof can be used to prove ownership of assets. One example is using something like zkAttestor. The basic idea is to attest to the ownership of assets against a certain block-header. Efficiency of zkSNARK-based attestation can be improved significantly by batching through proof aggregation (for example, using Halo2). There is an ongoing effort from Axiom (with overlapping authors of zkAttestor) working on this problem.
Proof of Liabilities: Existing Solutions
The idea behind proof of liabilities is to let the CEX publish a cryptographic accumulator R over the set of liabilities of the exchange (which we call the “liability set”) and a total liability B such that:
- The accumulator binds to the total liability B, i.e. the exchange cannot change their answer after commiting
- Any user can check that their assets are included in the liability set via a proof that is consistent with the total B and R
Vitalik provides two protocols that solve this problem, we discuss them below.
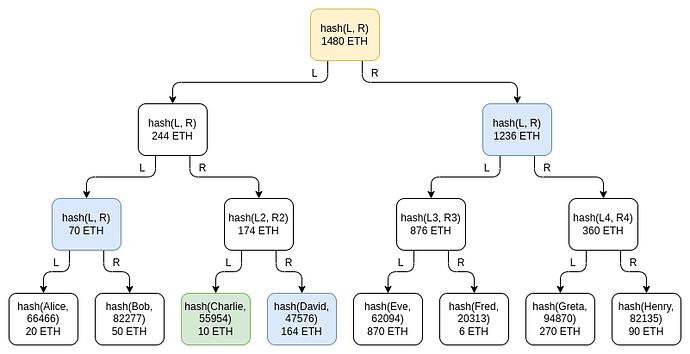
Solution 1: Merkle Sum Tree
Merkle Sum Tree is a special kind of merkle tree, in which each inner node contains the sum of the balances of its child tree. The great advantage of this scheme is its simplicity (not a bad thing!). In fact, since Vitalik wrote about his design, Mazars already built a proof of liability product for Binance (here). However, as we will articulate next, this solution has devastating privacy leakage.
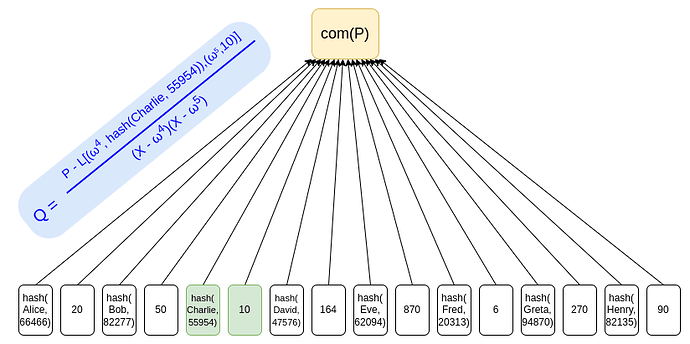
Solution 2: KZG - Customized IOP based Sum Proof (KZG-Sum IOP)
To improve the privacy and robustness, Vitalik proposed a second scheme[^1] based on KZG and a customized proof system based on an IOP.
As shown in the figure above, instead of committing each user’s username and balances in a merkle tree, we can commit a user’s username and balance at adjacent locations in a vector commitment like KZG. Each user only needs to remember her location (in the above example, Charlie’s username is committed in the index 4, his balance is committed in the index 5).
Next, to prove the summation of the balances, Vitalik proposed a customized IOP-based proof system for efficiency.
Unlike the Merkle Sum Tree solution, this preserves privacy for the user’s balance. A user doesn’t need anyone else’s balance to attest to the fact that their liability is included.
Problems with Existing Solutions
Merkle Sum Tree Solution
As mentioned in Vitalik’s blog post, Merkle Sum Tree solution (the one adopted by Binance now) suffers a huge privacy loss for both CEXs and its customers. In more detail:
When a user queries the CEX for a liability proof, the CEX needs to provide a merkle proof containing the balances of other users’ balances along the merkle tree. In the above example, the merkle proof provided to Charlie leaks:
- David’s Balance
- The sum of Alice and Bob’s balance
- The sum of {Eve, Fred, Greta, Henry}'s balance
By creating a number of spam accounts, adversaries can not only gain the information of real users balances, they can also discover the distribution of user’s balances across the CEX. What makes things worse is that this balance information can be correlated with other known infomation (such as on-chain data of token transfers). By correlating the balances, transfers on chain, and balance leakage from MST, many users’ identities can be inferred. This could lead to disastrous privacy concerns for customer data in CEXs.
We kill people based on metadata.
– Michael Hayden, Former Director of NSA and CIA
KZG - IOP Sum Solution
Compared with Merkle Sum Tree, KZG-IOP Sum is a well-balanced solution on a technical level; the major issues are at the practical and engineering level.
Very Large Trusted Setup
KZG-IOP Sum solution requires a trusted setup. Some big CEXs could have more than 200 million users. This could translate to more than 400 million elements in the vector commitment. Now, the biggest trusted setup so far (the Perpetual Powers of Tau) has an effective size of 2^{28} \simeq 270 \text{ million}. A trusted setup of at least twice this size would be needed. This requires a huge effort and also scarifices on decentralization since the larger the trusted setup size, the higher requirement that it places on the participants.
Requiring Constructing a New, Customized Proof System
In addition, Vitalik’s proposal, while elegant, requires building a customized proof system protocol. When implementing these systems using custom protocols we usually run into three main problems:
- In practice they are usually not more efficient (potential theoretical performance gain does not align with concrete performance)
- Vastly increased code complexity
- Reduced modularity with existing codebases and existing proof systems
- Harder to do a good security audit since the auditors are less familiar with these customized constructions
Our Solution: SNARKed Merkle Sum Proof of Liablities
We present below a simple SNARKed Merkle Sum Tree solution that addresses the above problems. There are two components to our protocol:
- A merkle sum tree (Same as Vitalik’s design) with Poseidon over the Goldilocks Field
- zkSNARK merkle proofs of inclusion of liabilities using Plonky2
Design Philosophy
In this setting, our primary concerns are:
- Construction time for the “Sum Commitment” - The CEX should be able run these as frequently as possible even if they have hundreds of millions of users
- Prover time for user queries - It should be as easy as possible for users to attest to the fact that their assets are accounted for. The harder it is, the less likely it is they will do it, and having to wait more than a few seconds will add friction.
- Large exchanges have on the order of 2^{28} users. Any public parameters the protocol uses should be practical to produce or verify.
In this setting, we don’t really require proofs to be very small (e.g. < 4KB). Since we are not verifying proofs on-chain, it’s totally fine if proofs are 2-3 MBs.
Given these design goals, we think Poseidon over the Goldilocks field with Plonky2 inclusion proofs is the correct choice because:
- No trusted setup - this eliminates the issue with KZG, where the setup is prohibitively large to run and/or verify.
- Commitment Performance - Poseidon on Goldilocks is one of the fastest arithmetic (ZKP friendly) hash functions yet have a very good concrete performance. Since CEX needs to compute hashes (in the worst case) in the order of 2^{28} at sub-microsecond per hash it takes on the order of a minute to build the merkle sum tree
- Prover Performance - Plonky2 is a very fast FRI-based PLONK implementation that can prove merkle tree inclusion (at sizes around 2^{28}) in seconds that can be verified in milliseconds
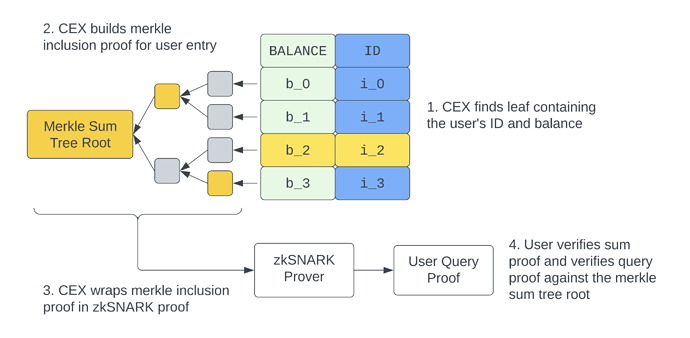
Individual User Proofs in More Detail
To complete a proof of liabilities argument, the CEX will need to have proof available to any individual user to show that her account/balance is included.
If a user with id i asks for a proof that their assets are included in the sum, the prover will proceed as follows:
- Create a merkle proof over the leaf for user i
- Wrap that merkle proof in a SNARK proving the following statement:
- Public Inputs:
- user ID i
- claimed balance b
- merkle sum balance-root (R, B)
- Private Witness:
- merkle inclusion proof \pi_{\textsf{MT}} for the leaf
- intermediate partial sums along the tree
- Statement:
- merkle inclusion proof verifier accepts against R and \pi_{\textsf{MT}}
- the balances along the inclusion proof sum to B
- no intermediate balance overflows
- Public Inputs:
- Send the SNARK proof \pi_{\textsf{SNARK}} for this statement to the user
Then, the user will accept this proof if the SNARK verifier accepts \pi_{\textsf{SNARK}} with b and i matching the user’s exchange details and (R, B) matching the known balance-root for the exchange.
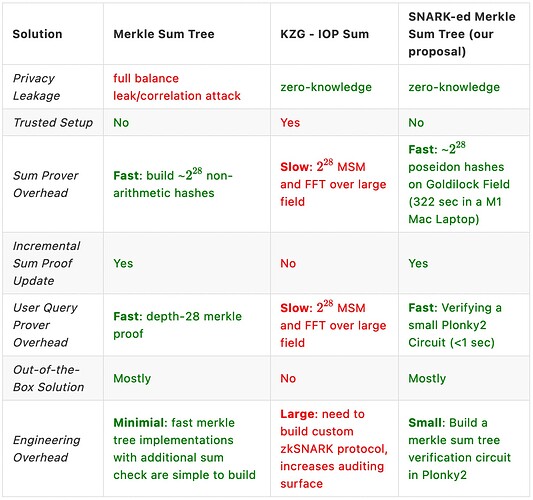
Comparing SNARK-based Proof of Liabilities with Merkle Sum Tree and KZG-IOP Sum
In our solution, for a CEX with 200 million users, we expect the proof size for the user proof be roughly 2-3 MB (we can tune the verifier/prover performance trade-off by changing the FRI blowup factor)and the proof verification time should be sub-second. While KZG-IOP Sum has a smaller proof size, the verifier efficiency is not the bottleneck of the PoSol implementation.
The key advantage of our solution is efficient commitment construction with a relatively low engineering complexity. SNARK-ed Merkle Sum Tree leverages the hardware acceleration friendly Goldilocks field to gain a good concrete tree-building performance (see the details in the table above) and as well as reusing a mature existing proof system implementation (plonky2) for fast user proofs.