Gossipsub’s Partial Messages Extension and Cell Level dissemination
or how to make blob propagation faster and more efficient
Thanks to Raúl Kripalani, Alex Stokes, and Csaba Kiraly for feedback on early drafts.
Overview
Gossipsub’s new Partial Message Extension allows nodes to upgrade to cell level dissemination without a hard fork. Increasing the usefulness of data from the local mempool (getBlobs).
There is a draft PR that specifies how Consensus Clients make use of the Partial Message Extension here: https://github.com/ethereum/consensus-specs/pull/4558.
Introduction
Fusaka introduces PeerDAS with EIP-7594. As explained in the EIP, erasure coded blobs are disseminated as columns of cells. The columns are typed as DataColumnSidecar. These columns are propagated via gossipsub to the network. If a node already has all the referenced blobs in a column from its local mempool, it can derive the DataColumnSidecar itself without waiting for Gossipsub propagation. It then also propagates the column to help with rapid dissemination. The IDONTWANT message of Gossipsub serves to supress these pushes from a peer that already has the IDONTWANT message.
In the case that all referenced blobs of a block appear in the the majority of nodes’ mempool, then reaching the custody requirement is fast. The data is already local. However, if even a single blob is missing then nodes must wait for the full columns to be propagated through the network before reaching their custody requirement.
Ideally we would disseminate just the cells that are missing for a given row. Allowing a node to make use of data it already has locally. That’s what Gossipsub’s Partial Message Extension does.
The Partial Message Extension allows nodes to send, request, and advertise cells succinctly. It is a change in the networking layer that does not require consensus changes, can be deployed in a backwards compatible way, and does not require a hard fork.
Partial Message extension, an overview
The full draft spec can be found at libp2p/specs.
Partial Messages behave similar to normal Gossipsub messages. The key difference is that instead of being referenced by a hash, they are referenced by a Group ID. The Group ID is application defined, and must be derivable without requiring the complete message. With a Group ID and a bitmap, a Node can efficiently specify what parts it is missing and what parts it can provide.
For PeerDAS, the Group ID is the block root. It is unique per topic. A full column is a complete message, and the cell is the smallest partial message. A cell is uniquely and succinctly identified by the subnet topic (the column index), Group ID (block root), and position in the bitmap. A node can start advertising and requesting cells as soon as it receives the block. Which is the soonest possible because the block declares the included blobs.
Cell-level dissemination with normal gossipsub messages is tricky at best. Each cell would have to be referenced by its full message ID (20 bytes), and nodes cannot request missing cells a priori; they must first know how a cell maps to its corresponding message ID. In contrast, with partial messages, nodes reference each cell with a bit in a bitmap, and can exchange information of what they can provide and what they need with partial IHAVEs and partial IWANTs.
Partial messages can be eagerly pushed to a peer without waiting for the peer to request parts, or they can be provided on request.
Gossipsub Partial Messages require application cooperation, as the application knows how messages compose and split. Applications are responsible for: - Encoding available and missing parts (e.g. a bitmap). - Decoding a request for parts, and responding with an encoded partial message. - Validating an encoded partial message. - Merging an encoded partial message.
Hypothetical example flows
To help build an intuition for how partial messages will work in practice, consider these two examples. The first example uses eager pushing to reduce latency, the second example waits for a peer request which can reduce duplicates at the expense of latency (1/2 RTT in this example).
For both examples, assume:
- Peer P is the proposer of a block. It knows about all blobs in a block.
- Peer A and B are validators.
- The first blob in the block was not shared publicly to A and B before hand, so they are both missing this single blob from their local mempool.
- P is connected to A is connected to B. P <=> A <=> B
Eager pushing
┌──────────────────┐ ┌──────────────────┐ ┌──────────────────┐
│ P │ │ A │ │ B │
└──────────────────┘ └──────────────────┘ └──────────────────┘
┌────────────────┐ │ │
│Proposes Block B│ │ │
└───────┬────────┘ │ │
│ ┌──────────────┐ │ │
├───│Forwards block│──▶│ ┌──────────────┐ │
│ └──────────────┘ ├───│Forwards block│──▶│
│ ┌──────────────┐ │ └──────────────┘ │
│ │ Eager push │ │ ┌──────────────┐ │
├───│cell at idx=0 │──▶│ │ Eager push │ │
│ └──────────────┘ ├──│cell at idx=0 │──▶ │
│ │ └──────────────┘ │
│ │ │
│ │ │
│ │ │
▼ ▼ ▼
Request/Response
┌──────────────────┐ ┌──────────────────┐ ┌──────────────────┐
│ P │ │ A │ │ B │
└──────────────────┘ └──────────────────┘ └──────────────────┘
│ │ │
┌───────┴────────┐ │ │
│Proposes Block B│ │ │
└───────┬────────┘ │ │
│ ┌──────────────┐ │ │
├───│Forwards block│──▶│ ┌──────────────┐ │
│ └──────────────┘ ├───│Forwards block│──▶│
│ ┌──────────────┐ │ └──────────────┘ │
│ │ IWANT │ │ ┌──────────────┐ │
│◀──│ idx=0 │───│ │ IWANT │ │
│ └──────────────┘ │◀──│ idx=0 │───│
│ ┌──────────────┐ │ └──────────────┘ │
│ │ Respond with │ │ ┌──────────────┐ │
├───│ cell@idx=0 │──▶│ │ Respond with │ │
│ └──────────────┘ ├───│ cell@idx=0 │──▶│
│ │ └──────────────┘ │
▼ ▼ ▼
Note that peers request data before knowing what a peer has. The request is part of the peer’s IWANT bitmap, which is sent alongside its IHAVE bitmap. This means data can be received in a single RTT when the peer can provide the data. In contrast, an announce, request, respond flow requires 1.5 RTT.
Publishing strategy
Eager pushing is faster than request/response, but risks sending duplicate information.
The publishing strategy should therefore be:
Eager push when there is confidence that this will be the first delivery of this partial message.
In a scenario with private blobs, it’s reasonable for a node to forward with an eager push when it receives a private blob.
In a scenario with sharded mempools, it’s reasonable for a node to eagerly push cells it knows a peer would not have due to its sharding strategy.
Some duplicate information is expected and required as a form of resiliency. The amount of duplicates can be tuned by adjusting the probability of eager pushing and the probability of requesting from a peer.
However, even a simple naive strategy should significantly outperform our current full-column approach by leveraging local data from the mempool. Duplicate partial messages would result in duplicate cells rather than duplicate full columns.
Devnet Proof of Concept
There is a work-in-progress Go implementation of the Partial Message Extension. There is also a patch to Prysm that uses partial messages.
As a proof of concept, we created a Kurtosis devnet using the patched Prysm clients connected to patched geth clients (to return partial blobs in the getBlobs call). Some nodes would build blocks with “private” blobs. When this happened other nodes would request only the missing “private” cells, and fill in the rest of the column with blobs from their local mempool.
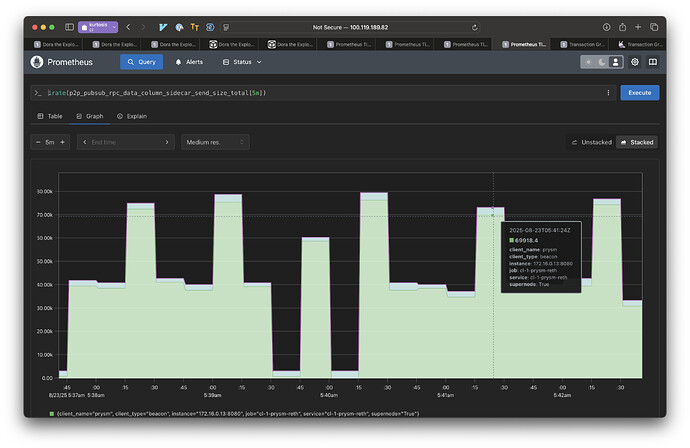
To get a rough sense of bandwidth savings we also created a smaller kurtosis network of just two “super” nodes, nodes that receive and send all columns. One of the nodes proposes private blobs. The means that getBlobs will fail to return a full column for the other node when the aforementioned node proposes.
We measured data sent for DataColumnSidecar messages without and with Partial Messages. The results show with Partial Messages, nodes send 10x less data. There are two reasons for this:
- The current Prysm implementation of Partial Messages never eagerly pushes. Nodes wait to see a request before responding with data.
- Only the requested parts are sent. If a column had a single private blob, we only send that one blob.
In this low latency environment (running locally with Kurtosis), IDONTWANTs are not effective. Hence we see a large benefit in simply not eagerly pushing data.
However, in the cases where there are private blobs, IDONTWANT would not be applicable, so the performance benefits here are still representative of higher latency more realistic environments.
Graphs:
This is an experiment with just two peers, but each pairwise interaction in a mesh with more peers should behave the same. The is the bandwidth used for disseminating data columns.
Mempool sharding
Future directions of mempool sharding will only make it more likely that nodes are missing some cells, and thus require some form of cell level dissemination.
“Row” based dissemination
Note that if a node is missing a cell at some index in one column, it’s likely missing cells at the same position in all other columns. One future improvement could be to allow nodes to advertise full rows to its mesh peers. The benefit is that a node fills all its missing cells for a row at once. The downside is the risk of larger duplicate messages.
Next steps
- Specify the getBlobs V3 api that supports returning partial blobs.
- Implement the Partial Message Extension in Rust libp2p. (in progress)
- Specify the partial message encoding of DataColumnSidecars. In Progress
- Integrate into CL clients.
- Deploy on testnets
- Deploy on mainnet
- scale blob count