Selecting Optimal Outbound Neighbors (SOON) for fast, bandwidth‑efficient propagation in P2P networks

[soispoke]

by Thomas and Marios - October 27th, 2025

Thanks to Marco, Yann, Anders, Caspar, Raul and Csaba for their valuable feedback and comments.

TLDR;

Ethereum’s P2P layer currently forwards messages such as blocks, attestations, and blobs to randomly selected peers, considering latency only weakly through peer scoring. As a result, messages often travel along slow or overlapping routes, increasing bandwidth usage and propagation delay.

In this post, we introduce SOON (Selecting Optimal Outbound Neighbors), a simple propagation rule that forwards to the fastest peers instead of random ones. It reduces latency and bandwidth simultaneously, preserves coverage, and can be adapted for different message types, while keeping GossipSub’s core design unchanged.

Introduction

Ethereum’s P2P Layer and the Forwarding Problem

Ethereum’s peer-to-peer (P2P) layer serves as the network’s transport system, responsible for propagating messages such as blocks, blobs, and attestations. This layer is built on GossipSub, a publish-subscribe protocol where each node maintains a set of connections known as peers. For every topic, a node selects a small subset of these peers of size K to form its mesh. These mesh peers are used for efficiently disseminating messages throughout the network. When a node first receives a message for a topic, it eagerly forwards the full message to its mesh peers (excluding the sender) and then “lazily” gossips the message ID to a subset of non-mesh peers using IHAVE messages. Those peers can later request the full message through IWANT.

Mesh peers are selected randomly from the pool of eligible peers, and is maintained dynamically via the peer-scoring rule. The mesh is replenished when its size falls below K_{\text{low}}, and pruned when it exceeds K_{\text{high}}. In practice, this produces a mesh that is mostly random and stable, rather than one that is reselected for each message.

This design provides robust coverage and reasonable latency while requiring few assumptions about the underlying network. However, it can also be bandwidth-inefficient and slower than necessary, since forwarding to mesh peers randomly, without considering latency, can end up propagating messages along slow paths.

In this post, we explore whether incorporating local “distance” signals, particularly round-trip times (RTTs), can improve the trade-off between latency, coverage, and bandwidth without changing GossipSub’s core architecture. To make this comparison precise, we introduce an explicit eager push budget \Delta \le K. Instead of forwarding to all mesh peers, a node only forwards to at most \Delta of the mesh peers. This allows us to compare local broadcast rules under a fixed budget \Delta. We then evaluate their performance numerically along three key dimensions: bandwidth, latency, and coverage. We begin by studying the problem analytically, in order to get a feeling of the mechanism that allows for optimizing for bandwidth, latency and coverage.

Theoretical foundations

Ethereum’s GossipSub overlay evolves dynamically by nodes joining and leaving the network and the peer selection mechanism which uses peer scoring and a mechanism for inclusion/removal of peers using GRAFT/PRUNE. In aggregate, this behavior produces a topology that we will approximate by a random graph. We assume this random-graph model for analysis and treat the topology as fixed. A broadcasting algorithm then specifies, for each node, which subset of its neighbors it forwards a newly received message to upon first receipt.

Graphs and metric models

Concretely, we represent the P2P network using:

1. Weighted random d-regular graph.
   We model the network as a weighted, random d-regular graph G = (V, E), where each vertex v \in V corresponds to a node, and each edge e = (u, v) \in E carries a weight w_e representing the observed round-trip time (RTT) between u and v. This graph captures both the topology (peer connections) and the metric (link latency) according to which we evaluate the quality of broadcasting.

2. Euclidean embedding.
   We also consider an approximate embedding of G in Euclidean space \mathbb{R}^2, where the Euclidean distance between two nodes corresponds roughly to their RTT, i.e. d(u, v) \approx w(u, v).

   Note. Real network latencies do not form a perfect Euclidean metric, since properties like the triangle inequality can be violated (e.g., w(a, c) > w(a, b) + w(b, c)). Nonetheless, practical embedding systems such as Vivaldi show that Euclidean coordinates often approximate RTTs well in expectation.

Performance objectives

We evaluate broadcasting algorithms along three dimensions:

• Latency (t_q).
  This is the total time needed on average to propagate a message to a fraction q of the network. Let us first define the shortest path between nodes u,v as

  p_{\mathrm{min}}(u,v):= \min_{p\in P_{u,v}} \sum_{e\in p} w_e

  where p=(u,...,v) is a specific path starting at u and ending at v and P_{u,v} is the set of all such paths. The sum runs over consecutive node pairs/edges in the path. Then we define t_q for 0 \leq q\leq 1 as

  t_q:= \mathbb{E}_{u} \max_{v\in V_q(u)}p_{\mathrm{min}}(u,v).

  Here V_q(u)\subseteq V is defined such that |V_q(u)|/|V|=q and v\in V_q(u) iff there does not exist v' \in \overline{V}_q(u) with p_{\mathrm{min}}(u,v')<p_{\mathrm{min}}(u,v). In simulations, we are concretely using t_{90} as the latency metric.

• Bandwidth overhead (D_{\mathrm{avg}}).
  Beyond the first successful delivery, each node may receive the same message multiple times as redundant copies. Let D_v denote the number of such duplicate messages received by node v. We measure the average bandwidth overhead by

  D_{\mathrm{avg}} = \frac{1}{|V|}\sum_{v \in V} D_v,

  which quantifies the average number of redundant messages received by a node. Since retries and lazy gossip are disabled in our simulations, this metric directly captures the redundancy due to the eager-push mechanism.

Note: In a random graph overlay, if each node propagates to \Delta neighbors, we can argue by symmetry that the number of received messages is in expectation also \Delta. Since only the first delivery is useful, this yields D_{\text{avg}} \approx \Delta - 1 redundant copies per node.

Minimizing both latency and bandwidth overhead simultaneously is non-trivial even with global knowledge of G. A spanning tree minimizes duplication but may increase latency depending on its root. Flooding, i.e forwarding to all possible peers, minimizes latency at the price of high duplication. Our interest is in broadcasting algorithms that balance these two using only local information and local actions. This excludes algorithms where information is shared across the network and/or nodes coordinate their actions.

Preserving short paths

In order to understand how we can reduce bandwidth while preserving low latency we begin by noting that this can be understood as the problem described as:

Remove as many edges as possible while preserving short paths between nodes.

To tackle this, consider the Euclidean embedding mentioned above. In geometric graphs, where nodes are connected to spatially close neighbors, paths between any two nodes have low stretch i.e p_{\mathrm{min}}(u,v) \approx d(u,v). Thus, the total path latency is indeed close to the minimum possible, corresponding to a direct edge between the two nodes. For us this means that if we had a P2P overlay corresponding to a geometric graph with radius r=\Theta((\log n/n)^{1/2}) the resulting broadcast latency would be approximately optimal.

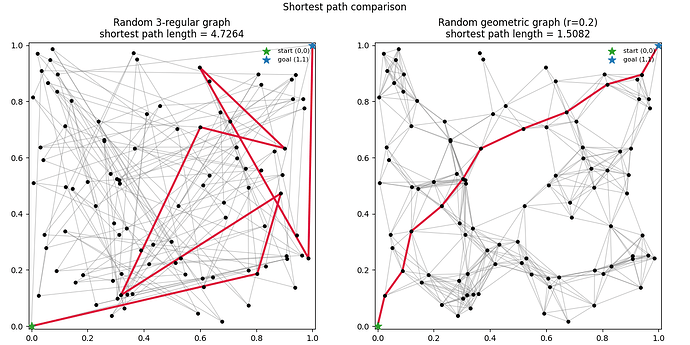
Figure 1 illustrates this: in a random 3-regular graph (Figure 1, left panel), a shortest path between distant nodes can meander; in a geometric graph with radius r=0.2 (Figure 1, right panel), paths track Euclidean geodesics closely, reducing stretch.

The primary question we are asking in this work can thus be phrased as follows:

Do broadcasting algorithms favoring propagation to low-RTT neighbors exhibit this low-stretch property in non-geometric overlays?

It is clear that the structure of GossipSub does not in itself give rise to a geometric graph topology – far from it. Nevertheless, what we want to explore in the following sections is whether favoring low-RTT neighbors can mimic this property by steering propagation along fast, short paths. Intuitively this will work better the larger the peer set is as it increases the probability of including nodes within the threshold radius r (indeed note that in the limit where the peer set is V, forwarding to those with \mathrm{RTT}<r induces a geometric graph by definition). Beyond the question of how well this works in practice, which we will seek to answer in the next sections, a natural complementary question to ask is how this selective forwarding affects the connectivity of the network. As we will see in the next section, as long as there is no correlation between the RTT distribution and the edge-set, broadcasting that favors propagation to low-RTT neighbors can reduce delay without affecting coverage.

Figure 1. Random graph vs. random geometric graph. Left: a random 3-regular graph. Right: a geometric graph with connection radius r = 0.2. Red edges show the shortest path between two distant nodes; geometric locality reduces path stretch.

Ensuring high coverage

To ensure high coverage we require that the subgraph induced by the broadcasting algorithm remains connected. Connectivity thresholds, also known as percolation thresholds, differ across random-graph models. Without going into any details here we note that in random d-regular graphs, for any fixed d \ge 3, the graph is connected with high probability. Similar results exist for other graph families.

Note that this threshold does not depend on edge weights and holds equally for weighted and unweighted graphs, provided that for the former edge existence and edge-weights are independent. If the peer-selection mechanism was biased towards low-RTT edges, topology and weights would become correlated, potentially improving latency but complicating theoretical guarantees of connectivity. We return to this trade-off when discussing hybrid and RTT-aware forwarding rules.

Bandwidth reducing broadcasting algorithms

In the following sections, we use numerical simulations to compare a set of local budget-\Delta broadcasting algorithms. When a node v receives a message from a peer u, we define:

• \mathrm{RTT}_{\mathrm{upstream}}: the round-trip time to the node that sent the message (the single upstream peer).
• \mathrm{RTT}_{\mathrm{downstream}}: the round-trip time to each candidate peer that v might forward the message to (the downstream peers).

In all algorithms, forwarding occurs only upon first receipt. Once v receives a message from u, the sender u is removed from v ’s neighbor set, \mathcal{N}(v), to prevent back-sending, which avoids redundant transmissions. We then consider the following algorithms in detail.

RTT-agnostic:

• Random: Propagate to \Delta mesh neighbors chosen uniformly at random (vanilla GossipSub forwards to all K mesh peers; we cap at \Delta for comparison).

• Coin‑toss: Propagate to each neighbor independently with probability p; if more than \Delta are flagged, keep a random \Delta.

RTT-aware:

• Δ‑fastest: Propagate to the \Delta neighbors with the smallest \mathrm{RTT}_{\mathrm{downstream}}.

• Downhill: Propagate to neighbors with \mathrm{RTT}_{\mathrm{downstream}}<\mathrm{RTT}_{\mathrm{upstream}}.

• Absolute-threshold: Propagate to neighbors with \mathrm{RTT}_{\mathrm{downstream}}\le T for some constant T.

Note: As mentioned earlier, Absolute-threshold with appropriately chosen input parameters will lead, by definition, to a geometric graph overlay in the limit where the peer set corresponds to the entire set. We introduce Δ‑fastest and Downhill as potentially simpler heuristics to Absolute-threshold.

Experimental setup

We evaluate each broadcasting rule via a discrete-event simulator configured to mimic Ethereum’s gossip layer.

• Graphs. Random d-regular graph G(N,d) with N{=}1500 and d=50.

• Per-topic mesh. Each node maintains a per-topic mesh of size D{=}8 (the GossipSub default). On first receipt, a node forwards eagerly to up to \Delta \le D mesh peers according to the selected rule.

• RTT models (edge-oriented, asymmetric).

  • Baseline: single_lognorm lognormal distribution with median 100 ms and shape \sigma{=}1.
  • Empirical: bimodal 60/40 mixture of lognormal distributions with median 20/200 ms and \sigma = 0.4/0.5 respectively.

• Eager success. q{=}1 meaning all sent messages are actually received.

• Bandwidth metric. D_{\text{avg}}: average number of duplicate messages per informed node (redundant eager transmissions).

• Lazy gossip disabled. The simulator models only the eager-push phase: no IHAVE/IWANT, and no retries. All counts reflect eager transmissions only.

• Latency metric. t_{90}: time to inform 90% of nodes (ms under the chosen RTT model).

• Coverage floor. \ge 0.90 when comparing latency at matched bandwidth.

• Estimation. Means and 95% CIs over independent graphs and random seeds.

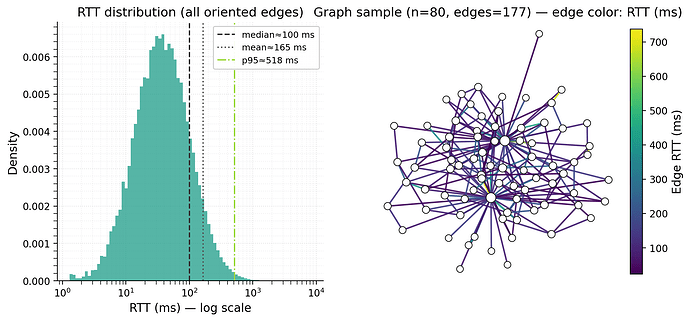
Figure 2. RTT distribution and representative topology. Left: density of oriented edge RTT samples on a log-x axis under the baseline single_lognorm (median 100 ms, \sigma=1). Right: induced subgraph (n=80, 177 edges) from the simulated G(N,p); edge color shows symmetric RTT (ms), and node size scales with local degree.

Note: We ran numerical experiments across multiple combinations of graph topologies (random, small-world) and RTT distributions (lognormal, bimodal). All combinations exhibited qualitatively identical behavior, so we present results only for the representative case of a random d-regular graph with the single_lognorm RTT distribution.

Results

Coverage vs. bandwidth

We first compare RTT‑agnostic (Random, Coin‑toss) and RTT‑aware (Δ‑fastest, Downhill, Absolute-threshold) rules on the coverage–bandwidth frontier.

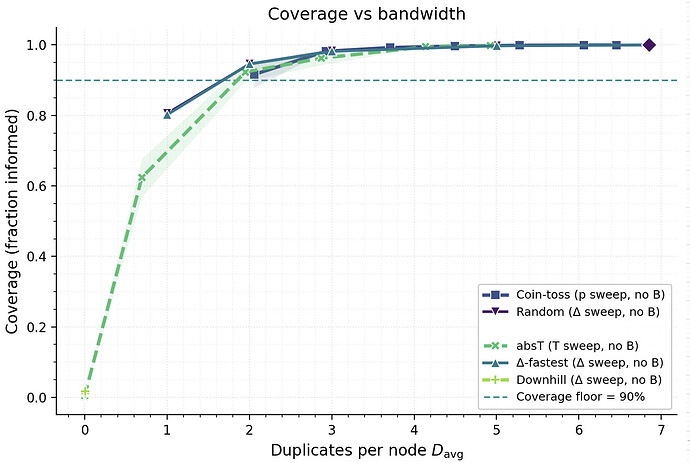
Given our experimental setup, Figure 3 shows that RTT-aware (Δ-fastest, fixed-T) and RTT-agnostic (Random, Coin-toss) rules trace nearly the same coverage–bandwidth frontier once the average duplicates D_{\text{avg}} exceed roughly 3\text{–}4. All four policies climb rapidly to ≥0.95 coverage and then saturate near full reach with overlapping CIs. The exception is Downhill, which can miss the coverage floor at low bandwidth because its relative threshold prunes too many candidates on already-fast nodes.

This near-overlap is consistent with what we discussed earlier, once average fan-out exceeds a small constant (≈3 in random d-regular models), connectivity is achieved with high probability. Moreover, because edge existence and edge weights are independent in our model, the RTT ordering at a node is a random permutation of its adjacency list. Selecting the \Delta smallest RTTs therefore yields a uniform random \Delta-subset of neighbors, preserving the connectivity distribution of random selection while improving the latency profile. As we noted before, the expected number of duplicates received in the case of the induced subgraph being random, d-regular is d. This explains why in Figure 3 the average duplicates track \Delta closely.

Figure 3. Coverage versus bandwidth. Fraction informed versus average duplicates (D_{\text{avg}}). Markers and parameters: ● Random (\Delta fixed at 8), ■ Coin‑toss (probability p\in[0.3,0.95]), ▲ Δ‑fastest (\Delta∈{2,3,4,6,8,10}), ◆ Absolute-threshold (T sweep), and ✦ Downhill. Observe that, as argued D_{\text{avg}} \approx \Delta - 1.

Bandwidth vs. latency

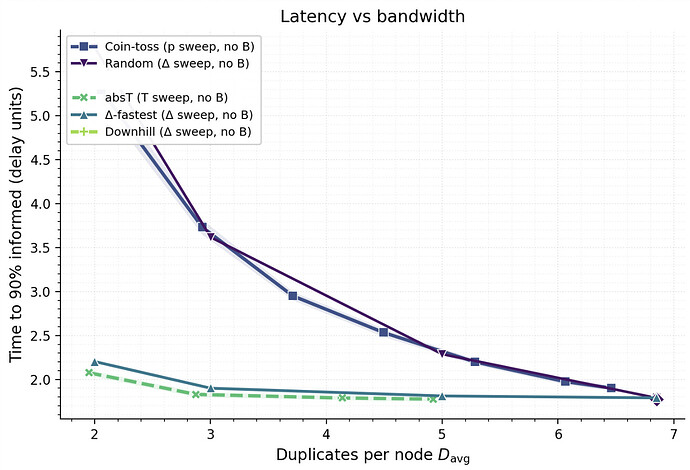
We examine the latency–bandwidth trade‑off by plotting the time to inform 90% of nodes (t_{90}) against the average duplicates (D_{\text{avg}}). Across the board, RTT‑aware rules achieve the same coverage at substantially lower latency than RTT‑agnostic baselines at the same D_{\text{avg}} (see Figure 4). The separation is most visible in the low‑bandwidth regime (\approx 3\text{–}5 duplicates). When increasing the number of neighbors to which messages are propagated (increasing \Delta) Randomand Coin‑tossapproach and reach similar values for t_{90} as Δ‑fastest and Absolute-threshold. This can be explained by the fact that in this regime fast paths, previously only in the subgraphs induced by Δ‑fastest and Absolute-threshold, are now also in the subgraphs induced by Randomand Coin‑toss.

This behavior aligns with the intuition from random geometric graphs (see Figure 1): forwarding along low-RTT edges preserves short paths, reducing end-to-end latency and answers the question we pose affirmatively.

The problem of determining an appropriate threshold value is non-trivial and furthermore might not be constant for a dynamically evolving network. We see however, that Δ‑fastest traces out a very similar t_{90} for a given number of duplicates by allocating the entire budget to the fastest peers. Δ‑fastest is also simple to implement: as long as \Delta is large enough to exceed the percolation threshold, it ensures good connectivity and high coverage while minimizing latency.

Overall, RTT‑aware propagation is the key to lowering latency at fixed bandwidth. Within that family of broadcasting algorithms, Δ‑fastest is seen as a good practical approximation to Absolute‑threshold: it delivers similar t_{90} at the same D_{\text{avg}} while being more practical to implement.

Figure 4. Latency versus bandwidth. Time to inform 90% of nodes versus average duplicates (D_{\text{avg}}). Markers and parameters: ▲ Δ‑fastest (\Delta\in{2,3,4,6,8,10}), ◆ Absolute‑threshold (threshold T sweep), ■ Coin‑toss (probability p), ● Random (\Delta fixed at 8). Shaded regions are 95% CIs.

Note. Downhill is absent because the figure filters runs that don’t meet the 90% coverage floor to compare latency fairly at matched bandwidth. In this configuration (no backbone; strict \mathrm{RTT}_{\text{downstream}}<\mathrm{RTT}_{\text{upstream}}), Downhill often prunes too many neighbors on already fast paths and does not reach the floor, so those points are excluded by design.

Random backbones

GossipSub’s robustness comes from its use of randomness. Forwarding to random peers helps ensure broad coverage and makes the network resilient to coordinated attempts to block propagation or split the network. We consider hybrid rules that mix RTT-aware forwarding with a small random backbone of size B: on first receipt, a node sends B eager copies to uniformly chosen peers (ignoring RTT), and uses the remaining \Delta - B copies according to the selected policy (Δ-fastest, Downhill, or Absolute-threshold).

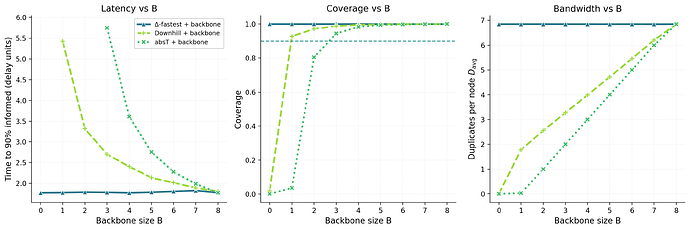
Figure 5 shows that adding a small random backbone improves robustness by breaking locality and counteracting the self-limiting effects of purely selective forwarding. For thresholded or conservative strategies such as Absolute-threshold and Downhill, even a few random eager copies keep the process supercritical and reduce latency noticeably. Once full coverage is reached, increasing B further produces diminishing returns, since random edges begin to replace already efficient links.

Figure 5. Backbone sensitivity at fixed total budget \Delta=8. Left: t_{90} vs. backbone size B. Middle: coverage vs. B (dashed line marks the 90% floor). Right: D_{\text{avg}} vs. B. Curves: ▲ Δ-fastest + backbone, ✦ Downhill + backbone, ◆ Absolute-threshold + backbone, with T^* chosen at B=0 to minimize t_{90} subject to the coverage floor. Shaded regions are 95% CIs.

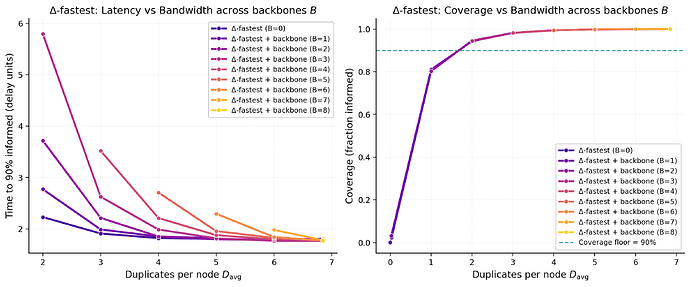
Δ-fastest is less sensitive to the backbone. As Figure 6 shows, allocating to enough fastest neighbors achieves the same coverage as configurations that include random peers, but at lower latency. This is in accordance with theoretical expectations (see corresponding section) since the RTT and edge distributions are independent. Under conditions that resemble a random graph with relatively high degree and a lognormal RTT baseline, local RTT ordering discovers near-shortest paths. In this setting, Δ-fastest captures the coverage benefits of randomness while spending attempts on faster links.

Figure 6. Effect of backbone size on Δ-fastest performance. Left: t_{90} versus average duplicates (D_{\text{avg}}) for Δ-fastest + backbone with varying backbone size B\in{0,1,2,\ldots,8}. Right: coverage versus D_{\text{avg}} for the same configurations; dashed line marks the 90% floor. For each B, the total budget is \Delta_{\text{total}}=B+\Delta_{\text{extra}}, where \Delta_{\text{extra}}\in{0,1,\ldots,5} controls the number of additional fastest neighbors beyond the random backbone. Shaded regions are 95% CIs.

Graph properties and peer-scoring interactions

As we mentioned before, a well-mixed, high-degree overlay is essential for RTT-aware selection to achieve high coverage. In sparser, more heterogeneous, clustered overlays, Δ-fastest can lead to network partitioning. A small random backbone can help alleviate this by allowing propagation between clusters.

In practice, Ethereum’s GossipSub peer scoring and mesh maintenance already preserve much of this beneficial mixing. Most scoring terms are independent of RTT, which lets the peer set refresh and remain well mixed over time. One prominent latency-sensitive component is P2: First Message Deliveries, which rewards a peer for being among the first to deliver messages in a topic; its weight can be set to zero to disable, or reduced via its decay and cap settings. P3: Mesh Message Deliveries counts deliveries within a short validation window and can create a softer implicit bias toward fast paths; it is also tunable through its window and weights. Removing these latency-sensitive terms maintains RTT independence in peer selection, preserving the random-graph-like mixing that ensures robust coverage.

SOON: A simple recipe for fast and resilient propagation

Based on the insights from our theoretical and empirical analyses, we propose SOON (Selecting near-Optimal Outbound Neighbors) as a practical policy that combines well-mixed connectivity with fast, RTT-aware forwarding.

1) Random peer selection.
Maintain random-looking connectivity via the peer-scoring rule. Keep updating peer set through periodic usage of GRAFT/PRUNE so the overlay stays well mixed throughout. Consider disabling P2 and P3 to maintain independence between peer selection and an RTT-aware propagation rule.

2) Optimally fast eager push with Δ-fastest.
Use Δ-fastest on first receipt. A practical default could be \Delta = 4 (this value could be adapted based on real network simulations and testnet data) to ensure a comfortable margin above typical percolation thresholds on random-like overlays while keeping duplication low. This routes scarce first-receipt attempts to the lowest-RTT neighbors and reduces t_{90} without harming coverage in well-mixed graphs.

Per-message (or per-topic) \Delta tuning. \Delta doesn’t have to be a single network-wide value. Set it to match each message type’s latency–bandwidth trade-off: use a higher \Delta for critical-path broadcasts (e.g., attestations) and a lower \Delta for large messages, such as blobs.

3) Keep lazy gossip as a safety net.
Continue to use gossip-pull (IHAVE/IWANT) as a backup against failures such as network separation induced by Δ-fastest. This is the primary hedge against edge cases in which Δ-fastest might underperform.

Why this works:
Δ-fastest exploits fast paths to lower latency. Lazy gossip acts as a robust fallback. With P2 reduced or disabled and P3 kept conservative, peer scoring does not introduce correlations between RTTs and the induced networks edge-set. This ensures that the overlay retains the random-graph topology and thus preserves global coverage even when each node only forwards to a small number of peers.

Future work

There are a number of open questions we want to address in the future.

First, we need to bring the simulations closer to the actual network configuration governing Ethereum’s P2P layer. As we have seen, some of the broadcasting algorithms exhibit rather similar behavior, and their adequacy can only be determined once simulations in realistic environments have been carried out. The idea is to run simulations using Shadow after implementing policies in the libP2P libraries, before moving to devnets and monitoring key metrics there.

Second, we will study the interaction between SOON and lazy-gossip semantics, as implemented by GossipSub extensions such as partial Messages.
These extensions introduce explicit mechanisms for balancing eager and lazy push: instead of forwarding entire payloads, nodes can advertise or request subsets of large messages like blobs (and its cells). While currently designed for blob dissemination, similar approaches could extend to other message types through erasure coding or block chunking. SOON complements this design by optimizing who receives the limited eager transmissions, while the extension determines how much of each message (or which parts) are sent eagerly versus lazily. We plan to evaluate hybrid schemes where SOON’s Δ-fastest selection governs the eager subset (e.g., the peers chosen for initial cell dissemination) to better understand how RTT-aware forwarding interacts with explicit lazy-push semantics and data chunking strategies.

We also want to explore counter-based heuristics used in gossip broadcasting to further reduce redundancy. For instance, a node may start a counter on first receipt and suppress re-transmission if enough confirmations arrive within a short window \Delta t. In practice, such a counter could simply be set by the inherent node delay due to node-specific tasks (verification, attestation etc.) and other factors such as queuing. Within the context of partial messages and potential chunked or erasure-coded, such heuristics could operate at a finer granularity: deciding dynamically which cells, chunks, or coded fragments to retransmit based on local reception density and observed RTTs. We will examine how these adaptive suppression strategies interact with RTT-aware forwarding and whether they can be combined with SOON to achieve near-optimal propagation efficiency under varying network conditions.

We can also broaden and accelerate propagation with a source-only rule. On first broadcast, the source node could use a larger \Delta and allocate its budget randomly to seed the message into several “far-apart regions” of the network. Relay nodes could then apply the \Delta-fastest rule, pushing the message quickly within each seeded region. This hybrid widens the initial footprint while keeping subsequent hops latency-optimal, and it lets us tune (\Delta_{\text{src}}) by message type and overlay conditions to balance duplication, coverage, and speed.

Finally, different broadcasting algorithms may be more vulnerable to network errors (e.g., outages) or to attack vectors from malicious actors who try to increase overall latency or bandwidth usage. Another possible malicious intent is to discover message sources: with less randomness and more structure, it may be easier to deanonymize senders. In this note, we have not analyzed such dishonest behavior, but it must be an integral part of any performance evaluation.