This post summarizes a paper draft from our research at Butter, focusing on governance mechanisms in AMMs with protocol fees. Our exploration is inspired by innovative ideas like Votes as buy orders: a new type of hybrid coin voting / futarchy and Governance mixing auctions and futarchy. This research aims at proposing new pathways for enhancing protocol fee governance. We’re eager for community feedback on the proposed attack’s viability and comments on the overarching mechanism design objectives.
Protocol fees in AMMs are controversial (even barring legal considerations, which we will not consider here). They are a method for providing returns on original R&D investment by assigning value to governance tokens. They form a rent that drains value out of AMMs (reducing LP rewards) and thus reduces AMM users surplus.
Below, we suggest a simple Uniswap v2-based CFMM model (generalizable to multiple pools and v3) and a related competitive equilibria analysis that shows how an AMM can be outcompeted by a subsidized fork.
Next we will show how this opportunity can be harnessed by LPs to perform a coordinated attack on the original protocol to increase their LP returns, in the form of deploying a fee-less AMM fork and a funding contract.
Last, we will reason about objectives in a mechanism design setting. We will show that the possibility of the attack acts as a grim trigger on governance, effectively limiting token-governance extractible value (GEV), thus increasing the efficiency of the protocol in a myopic way. But we will also note that R&D investment payoffs are partly hindered by this mechanism thus potentially reducing welfare of AMM users and Ethereum users on the longer term.
Competitive Equilibria Analysis
Suppose two AMMs, each consisting of a single pool with the same two tokens. The only difference between both AMMs will be R_1, R_2 the reserves and V_1, V_2 the swap volumes per unit of time.
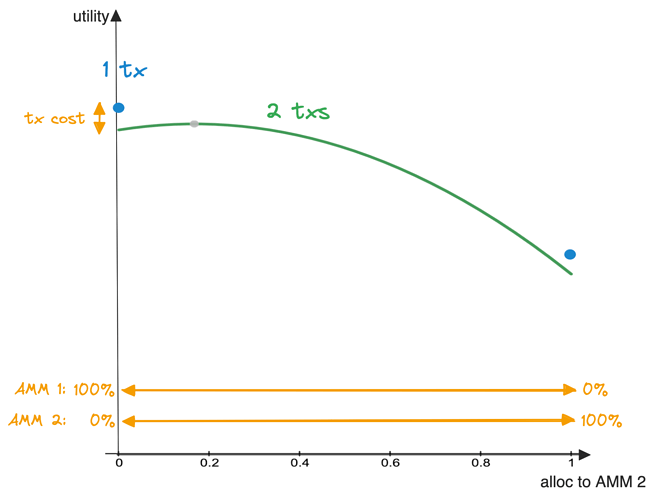
From the point of view of a swapper willing to allocate his swaps, the only distinction will be the slippage costs, which will be lower in the AMM with larger reserves. The swap allocation utility will have a cost term looking like -\frac{(1-x)^2}{R_1}-\frac{x^2}{R_2} (see figure below) with x the ratio (between 0 and 1) allocated to AMM 2 versus AMM 1. Hence, swappers performing small swaps will prefer exclusively using the AMM with larger reserves.
Allocation utility for small LPs will look like (1-x)V_1/R_1 + xV_2/R_2. Hence rational small LPs allocate all of their reserves towards the AMM with larger existing reserves.
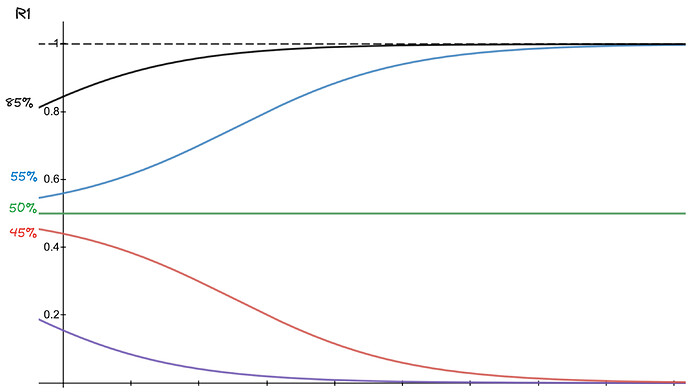
Both these conclusions combined prove an intuitive fact: on a long enough timeframe, the AMM with larger reserves and volume will accrue monopoly over liquidity. This is a classic network effect, as visualized in a simplified simulation below.
Starting R_1 proportion on the y axis, time on the x axis. If R_1 is more than 50% then liquidity will end up on AMM 1 entirely on a long enough timeframe.
Now, suppose that AMM 1 activates a protocol fee forever. In AMM 1, LPs payoffs as a function of their allocated reserves get updated from a factor (1-\gamma)\frac{V_1}{R_1} to a factor (1-\gamma-\rho)\frac{V_1}{R_1}, with 1-\gamma the LP fees and \rho the protocol fee (notation from Angeris et al., 2019).
Intuitively, the -\rho term will move upwards the %age threshold above which R_1 needs to start so network effects end up in favor of AMM 1 (it will be > 50%).
Suppose that AMM 2 adds a subsidy to its LP rewards, so payoffs will have two terms: (1-\gamma)\frac{V_2}{R_2}+ \sigma with \sigma the subsidy factor.
Intuitively, \sigma will as well move upwards the %age threshold mentioned above. With a large enough subsidy, the threshold can be made arbitrarily close to 100%.
Analyzing the equilibrium of this allocation game yields a minimum value for the subsidy, above which the network effects are systematically reverted in favor of AMM 2. With a big enough subsidy, AMM 2 can drain all liquidity from AMM 1.
Modelling LP risk appetite and switching costs in a straightforward fashion, our paper produces some tentative calculations to evaluate the total amount of the subsidy, which turns out reasonable: for every $100 in reserves, the total subsidy (over the lifetime of AMM 2) would amount roughly to $10.
Please note that these calculations are done under strong assumptions which would require relaxing to be more realistic. Notably, this simplified model doesn’t take into account other important factors like strategic assets (brand, IP).
Attack
We will design here a stylized attack on AMM 1 in case the protocol fee is activated forever. This will help us reason about what kind of effect can be produced on AMM 1’s governance.
Let’s consider the following attack setup:
- Attackers: LPs.
- Protocol under attack: AMM 1, including its governance.
- Attack vector: forked AMM contract with subsidy, funding mechanism contract.
- Gain for attackers: \rho minus an eventual participation in funding mechanism.
The funding mechanism contract is needed to produce the minimum subsidy discussed above, to provoke a liquidity drain from AMM 1 to AMM 2.
Assuming that AMM 2 will still have parameters to be governed, we suggest that there is a class of mechanisms for governing these parameters by auctioning off their control. Such mechanisms will produce a seller surplus.
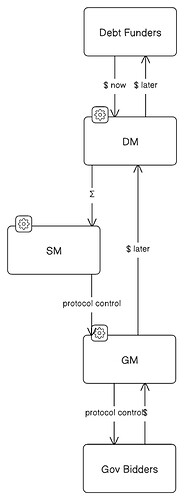
The subsidy would then be produced by a debt instrument funded by the auction mechanism, in the following setup:
DM: Debt Mechanism depending on the total amount of the subsidy
SM: Subsidy funding Mechanism which produces a subsidy to AMM 2’s LPs
GM: Governance Mechanism for AMM 2 based on parameter auctions
Gov Bidders: Bidders in the parameter auction.
Knowing that Uniswap v2 has no parameter to be governed and Uniswap v3 has only the addition of new fee levels, another approach to funding needs to be considered.
The subsidy can be produced by the attackers themselves, as long as its profitable for them. We suggest that such a crowdfunding mechanism is achievable (interim-rational for LPs to allocate some of their funds in) as the difference in expected payoff from an AMM with no fee compared to an AMM with fees is strictly positive:
To be credible, such a crowdfunding design would need to lower coordination costs for LPs. This is out of the scope of this first analysis, but some ideas can include fractionalized meta-LPs which keep a share of their LP gains to pay the fork subsidy.
This shows that by switching the protocol fee on forever, AMM 1 risks being depleted of its liquidity.
Now, supposing that the protocol fee can be adjusted by AMM 1’s governance, the existence of the attack produces a dynamic upper bound on \rho(t), the protocol fee as a function of time. The intuition for this is that raising \rho too much will produce some excessive liquidity drain to AMM 2, hence reducing the payoff of governance tokenholders.
Hence the attack provides a limit to the governance extractible value (GEV) of AMM 1. We will see in the next section how minimizing GEV might not be a good outcome, depending on our objectives.
Please note that several parts of this attack still need to be ironed out, notably as it relies on strong properties of the funding mechanism. But properly defining this funding mechanism and a broader class of applicable funding mechanisms goes beyond the scope of this post. Also, producing model for \rho(t) and its upper bound is still in the works.
Mechanism Design: Approaches
The above attack increases the LPs surplus at the expense of UNI tokenholders. But, as more value is kept in reserves, slippage costs are kept lower and consequently social surplus is increased.
We can assume that the existence of the fork and of the funding contracts plays a similar role to that of a grim trigger on AMM 1’s governance, forcing it to regulate its protocol fee. Hence the name of this mechanism: Grim Forker.
Interestingly, this mechanism provides a credible exit alternative (in the Exit or Voice paradigm) in the form of a coordinated fork.
Nevertheless, this misses the R&D investment game which requires that investors are rewarded for their early risk taking.
We can argue that giving myopic LPs too much power in this bargain can reduce investors gains to the extent of thwarting future R&D investment. Consequently, this would reduce overall welfare on a longer timeframe, possibly hurting the DeFi and Ethereum ecosystem.
If this analysis withstands scrutiny and aligns with real-world data, it suggests that:
- There exists a class of mechanisms that reduce protocol-fee Governance Extractible Value.
- Governance of these on-chain protocols should take these into account, notably by dynamically adjusting the protocol fee.
Further research could draw on the approach of this paper to produce formal results about on-chain protocols investability through governance tokens.