Linea’s sequencer proves a 30m gassed block of transactions in 5 minutes. Here’s its setup:
- On a 96 cores machine with 384 GB of RAM (hpc6a.48xlarge on AWS)
- In 5 minutes (only including the inner-proof)
So is it possible to reduce the proving time and, at the same time, obtain decentralization guarantees? We have an idea.
Overview
Almost all of the L2 sequencers are closed-source, intellectual property, and thus protected behind centralized setups. To cram that much power into an entity requires a great deal of justification today. To decentralize the flow, on the other hand, one has to accept certain amounts of delay and noise usually found in decentralized compute networks.
zkVMs, recursion, and Risc0’s approach
Any zkVM toolset puts a certain upper bound on the maximum number of cycles(roughly speaking 1 cycle equals 1 operation) it can prove in one go. This is usually done for efficiency reasons. For Risc0, a RISC-V general zkVM, it is 2^24 ~ 16.78m cycles. With recursion, proving infinitely sized programs are made possible. So the solution is to divide a large program into individual sub-programs(called segment in Risc0 jargon) and have them proved one by one and aggregate the proofs into a final proof as if the whole program was proved in one go. For example, consider proving a 1b cycles program. With 16.78M maximum segment size limit, one ends up proving 60 segments. The upper bound for segment size limit is not the end of story however and one can customize it into a well-known range of [2^13 - 2^24]. Each segment limit size needs specific memory requirements shown on Table 1:
Extrapolating Table 1’s values, we get 50m cycles for a program that needs 384gb of memory, in order to be proved in Risc0. Recall that Linea’s prover uses 384gb of memory to generate proofs. This is a naive 1-1 translation, but we can treat it as baseline for further testing. So, with this assumption, should one write Linea’s sequencer logic in Risc0, she would end up with a program that is 50m cycles long. Doubling cycles to ~90m, to account for aggregation won’t hurt here.
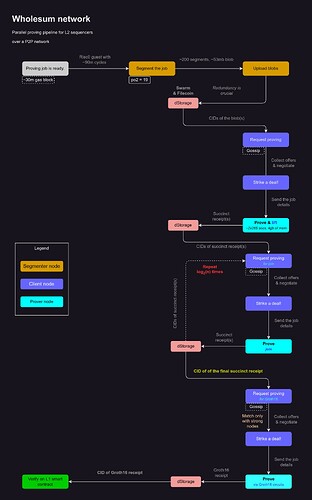
Segmentation, parallel proving, and decentralization
Recursion is a powerful idea in zkVM proving. With recursion once can get to prove seemingly large programs very quickly assuming she has a prove-ready network of machines. Table 2 shows a segmented prove session for a 90m cycles program on a pretty weak machine(8+ years old, Intel core i7 5500U(2C 4T), 16gb memory):
As you can see, different segment size limits result in varied proving regimes. In Table 2, two columns are colored in green, 2^18 and 2^19. Consulting Table 1, we would get 2gb and 4gb of required memory to prove them respectively. These columns are sweet spots for any zkVM proving network whose nodes are presumably weak. Focusing on the 2^19 segment size limit, to prove a 90m cycles program, one would need at least 168 nodes in order to prove the program in 4 minutes and 9 seconds. But 168 nodes is a faulty assumption. In reality, if a p2p network is to undertake the proving job, it needs to have redundancy values of 1:4 and above. The redundancy accounts for noise that is a feature of any p2p network. With 1:4 redundant nodes, 1 in every 5 nodes is assumed to be honest and the rest are time wasters. So, a 1:4 redundant p2p network needs at least of 840 nodes to get the job done.
Assuming that the proving network is p2p, one can expect to obtain decentralized guarantees en route.
Conclusion
Here we introduced an imaginary setup to decentralize and improve L2 sequencer proving times. If the claim turns out to be legit, we would expect to improve the overall proving time for any zkVM application area. In addition, the setup provides decentralization guarantees as a side effect. While everything looks nice, we, at Wholesum network would like to put this setup to test and see if it works in action. If successful, a p2p verifiable compute network of 10,000 weak nodes can handle up to 10 Linea like L2s.
A somewhat more expanded version of this post is also available here.
We appreciate your feedback.