Vortex : building a prover for the zk-EVM
Alexandre Belling and Azam Soleimanian, ConsenSys R&D
In this post, we present the recent developments of the proof system that we are using for Consensys’ zk-EVM, first presented in this post and then further expanded in this post. While our proof system is still under development and will gradually be improved over time, its most recent version is described in this paper.
The structure of the prover
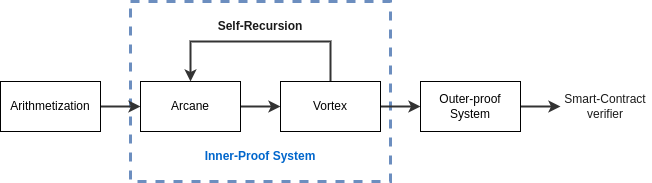
The proof system is mainly organized as a successive-compilation-step architecture. The “Arithmetization” is the set of constraints as expressed in the original posts. At a high level, the zk-EVM arithmetization describes the EVM as a set of registers and their values over time (e.g columns). The columns constituting the zk-EVM are bound to each other by constraints of various natures (inclusion, permutations, arithmetic constraints, etc). For more details, we advise the reader to go through the above-mentioned posts.
Thereafter, the zk-EVM arithmetization is compiled by Arcane, whose role is to convert the zk-EVM arithmetization into a polynomial-IOP. It mainly leverages known techniques from Halo2, Plonk, Cairo, etc. From then on, we instantiate the polynomial-IOP into a concrete proof system using Vortex, a polynomial commitment scheme at the core of our proof system. Vortex is a plausibly post-quantum and transparent polynomial commitment scheme based on a lattice hash function. Although Vortex has O(\sqrt{n}) proof size and verification time, it is equipped with a Self-Recursion mechanism which allows compressing the proof iteratively.
Once the proof is shrunk enough through self-recursion, we add a final compression step using an outer-proof system (today Groth16, Plonk in the future). This final compression step ensures that the proof is verifiable on Ethereum.
Lattice-based Hash function
As mentioned in the above section, Vortex makes use of a hash function based on the Short Integer Solution (SIS) (and its usual variants). We think it offers the best tradeoffs between security, computation speed, and arithmetization-friendliness.
- Security: the collision and preimage resistance of our hash function are directly reducible to SIS. Additionally, with the recent developments of NIST-PQC contest, the research community has developed numerous frameworks to benchmark the hardness of lattice problems.
- Execution-speed on CPU: ring-SIS hash functions require computing many small FFTs for each. This makes them an order of magnitude faster than EC operations (even with MSM optimization) and other SNARK-friendly hash functions.
- The hash function can potentially work with any field (in fact, it’s not even required to have a field). This makes them easier to use for recursion.
- They are somewhat arithmetic-friendly: all that is required to verify SIS hashes in a SNARK are range-checks and linear combinations with constants.
Status of the implementation
While the implementation work of the prover is in progress, we have already implemented a good part of it. In the current stage of the implementation we have;
- The prover relies on the bn254 scalar field all the way from the arithmetization to the outer-proof
- The SIS hash instance relies on the “original” SIS assumption (i.e. not the ring one) and uses n=2 and bound=2^3 on the bn254 scalar field. While it is in theory the slowest set of parameters that we present in the paper, it is also the simplest to optimize. With that, our hash function has a running time of ~500N ns where N is the number of field elements to hash
With the latest progress of the arithmetization and of the prover implementation, we are able to prove the execution of
- A 30M gas mainnet block,
- On a 96 cores machine with 384 GB of RAM (hpc6a.48xlarge on AWS)
- In 5 minutes (only including the inner-proof)