Lattice-based signature aggregation
This is joint report by David Nevado, Dohoon Kim, and Miha Stopar.
In Ethereum’s Proof-of-Stake, BLS signatures are used to aggregate attestations from multiple validators into a single, compact signature. However, BLS is not quantum-secure, and in a post-quantum future, it will need to be replaced. One promising direction is lattice-based aggregation, such as the recent Aggregating Falcon Signatures with LaBRADOR, which explores how to efficiently aggregate post-quantum Falcon signatures while maintaining small size and fast verification.
While LaBRADOR offers a promising approach to aggregating Falcon signatures with compact proofs (~74 KB for 10,000 signatures), other post-quantum alternatives exist. One is using STARKs to prove in zero knowledge that many hash-based signatures are valid. These approaches typically result in larger proof sizes—around 300KB for 10k signatures—but benefit from faster verification times.
At the conclusion of this write-up, we compare the LaBRADOR approach with a recent hash-based signature aggregation method. In that scheme, signatures are instantiated with Poseidon2, while aggregation relies on Keccak for Merkle-tree-based polynomial commitment schemes. The aggregation itself consists of arithmetizing the signature verifier within a Plonk-style proving system.
LaBRADOR is a relatively new protocol, and implementation support is still limited. While some Rust implementations are emerging, they are not ready yet, leaving the original C reference code as the main option for now. For benchmarking, we used the agg_sig.py script from the Lazer repository, which wraps the LaBRADOR C implementation. Below, we first present some benchmark results, and then explain how the Lazer approach differs from the approach described in the original paper, Aggregating Falcon Signatures with LaBRADOR.
Performance results
Approach:
We used our fork of LaBRADOR, which includes modifications to support larger signature batches (exceeding 2,000 signatures). The modifications were made to be able to increase the modulus to approximately 2^{48} to handle the larger intermediate values that arise during aggregation.
Results:
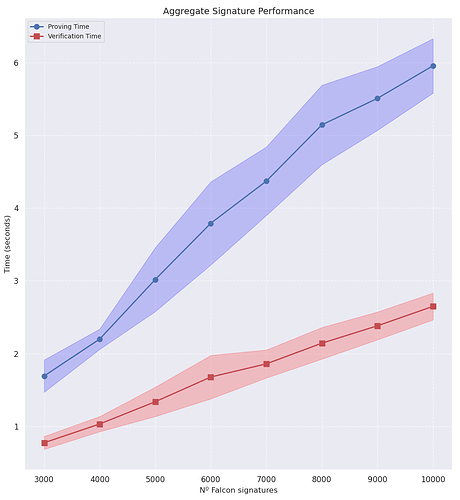
We measured proving times for the aggregation of batches between 3,000 to 10,000 Falcon-512 signatures. Benchmarks are obtained with single-thread executions on a 11th Gen Intel(R) Core(TM) i5-11400H @ 2.70GHz processor.
| # Signatures | Proving Time (s) | Verification Time (s) | Proof Size |
|---|---|---|---|
| 3000 | 1.6921 ± 0.2220 | 0.7739 ± 0.0888 | 77.83 KB |
| 4000 | 2.1991 ± 0.1403 | 1.0321 ± 0.1044 | 69.82 KB |
| 5000 | 3.0182 ± 0.4394 | 1.3380 ± 0.2021 | 72.45 KB |
| 6000 | 3.7914 ± 0.5716 | 1.6779 ± 0.2989 | 72.11 KB |
| 7000 | 4.3709 ± 0.4716 | 1.8586 ± 0.1928 | 71.83 KB |
| 8000 | 5.1447 ± 0.5469 | 2.1430 ± 0.2175 | 74.02 KB |
| 9000 | 5.5085 ± 0.4382 | 2.3821 ± 0.1915 | 72.27 KB |
| 10000 | 5.9565 ± 0.3750 | 2.6492 ± 0.1848 | 74.07 KB |
Note: While not shown in the graphs, this configuration supports even larger signature batches. Smaller batches (<2,000 signatures) achieve better performance since the modulus can be reduced to 2^{40}, lowering proving/verification times and proof size.
Key-takeaway:
10k Falcon-512 signatures can be aggregated with LaBRADOR resulting in:
- 74.07KB proof size.
- 5.95s proof generation.
- 2.65s proof verification.
From these results, the verification time stands out as the biggest obstacle for adoption. We analyzed verification in order to improve its performance.
Verification breakdown
The aggregation of Falcon signatures is carried out using a packed proof and the Dachshund frontend (see the Lazer paper for a brief descripton of Dachshund) provided in the LaBRADOR library. We profiled the verification process in the Dachshund test to identify bottlenecks and potential optimization opportunities. While we attempted to improve the original verification times through parallelization, these efforts were unsuccessful.
Analysis
Verification of a packed proof takes 1.2510 seconds and occurs in composite_verify_simple, which consists of two steps:
- simple_reduce: Derives the original composite statement
tstfrom the simple statementstand proofp(1.1356s, ~90% of total time). - composite_verify: Verifies
pagainsttst(remaining 10%).
Given its dominance, we focused on optimizing simple_reduce.
simple_reduce analysis
With a 48-bit modulus, the constant LIFTS = 3. The LIFTS loop consumes 77% of the runtime, but its sequential dependency (due to Fiat-Shamir challenges) prevents parallelization.
| Function | Time (s) | % of Total Runtime |
|---|---|---|
init_statement() + betasq |
0.0000 | 0.00% |
reduce_simple_commit() |
0.0000 | 0.00% |
reduce_project() |
0.0451 | 3.97% |
init_constraint() |
0.0000 | 0.00% |
| LIFTS loop (3x) | 0.8800 | 77.50% |
free_constraint() + cleanup |
0.0016 | 0.14% |
simple_aggregate() |
0.1067 | 9.40% |
aggregate_sparsecnst() |
0.0969 | 8.53% |
reduce_amortize() |
0.0053 | 0.47% |
| Total | 1.1356 | 100% |
Within the loop, we found several functions that are candidates for optimization. In particular, collaps_jlproj_raw().
LIFTS loop breakdown (per iteration)
| Function | Avg Time (s) | % of Total Runtime |
|---|---|---|
collaps_jlproj_raw() |
0.1166 | 10.27% |
polxvec_setzero() |
0.0178 | 1.57% |
simple_collaps() |
0.0537 | 4.73% |
reduce_lift_aggregate_zqcnst |
0.1053 | 9.27% |
| Total (per iteration) | 0.2934 | 25.84% |
| Total (3 iterations) | 0.8802 | 77.51% |
Optimizations attempts
LaBRADOR is heavily optimized with AVX-512 instructions but remains single-threaded. We explored parallelization but encountered challenges:
-
Fiat-Shamir Dependency:
The derivation of FS challenges is unavoidably sequential and this limits parallelization opportunities. -
Matrix Operations:
Parallelizingpolxvec_jlproj_collapsmat(30% ofsimple_reduce) with OpenMP degraded performance, likely due to:- False sharing (thread contention for cache lines).
- Memory bandwidth saturation (AVX-512 already maxing bandwidth).
However, further profiling is needed to isolate the root causes.
Comparison: Lazer and Aggregating Falcon Signatures with LaBRADOR
At first look it might appear that the technique from Aggregating Falcon Signatures with LaBRADOR is quite different from the Lazer one, but that’s actually not the case.
Let’s first observe how the aggregation of Falcon signatures works, and then dive into the differences between the two approaches.
Falcon signatures
The Falcon signatures consists of (s_1, s_2) such that:
where \mathbf{h} is part of a public key and \mathbf{t} is hash of a message.
We are proving the knowledge of \mathbf{s}_1 and \mathbf{s}_2 with a proof system that uses some other modulo than q, so the equation is rewritten into:
for some polynomial \mathbf{v}.
Aggregation of the Falcon signatures
We want to aggregate N Falcon signatures, that means proving:
for i=1,...,N.
Note that q is modulus from the Falcon scheme and the equation needs to hold in R_{q'} where q' > q, but with the same ring degree d. There must not appear a wrap-around modulo q' in the equation in order to prove that the equality holds over R.
The paper Aggregating Falcon Signatures with LaBRADOR uses LaBRADOR as a proof system. At the time the paper was submitted, LaBRADOR could not be used without some additional constraints due to the issues we describe below. The LaBRADOR source code—along with its Dachshund frontend—was released later, and in fact, Dachshund frontend directly addresses the very issues that initially prevented LaBRADOR from being used as-is.
Issue 1: norm check
The norm check using the Johnson–Lindenstrauss projection in LaBRADOR is both approximate and applies to the entire witness at once. This approach is now referred to as the Chihuahua frontend in the LaBRADOR source code. In contrast, the Dachshund frontend performs norm checks on each witness vector individually. Recall from above that in the context of signature aggregation, we have multiple witness vectors: \mathbf{s}_{i,1} and \mathbf{s}_{i,2}.
Since Dachshund had not yet been released, the paper was written assuming the use of the Chihuahua frontend. This frontend proves that the norm of the entire witness (i.e., all witness vectors combined) is small—an approach suitable for certain applications.
The idea of the Johnson–Lindenstrauss projection is to use random projection matrices \Pi: for the witness \mathbf{s}, the projection \Pi \mathbf{s} (a matrix-vector multiplication) is computed, and the verifier directly computes the norm of the projected vector. There’s a lemma stating, roughly, that if the projection is small, then the original vector is also small: if |\Pi \mathbf{s}|_2 \leq \sqrt{30} b for some bound b, then |\mathbf{s}|_2 \leq b. It must also hold that \sqrt{\lambda} b \leq \frac{q}{C_1} for a security level \lambda and some constant C_1. This imposes constraints on the modulus q used in the aggregation scheme—one of the reasons the paper uses a larger modulus q' > q instead of Falcon’s original modulus q.
However, in the case of signature aggregation, it is necessary to prove the smallness of each individual witness vector (all \mathbf{s}_{i,1} and \mathbf{s}_{i,2}) which is precisely what Dachshund is designed to support. Since Dachshund was not yet available, the authors of the paper instead introduced additional explicit constraints to enforce norm bounds on the individual witness vectors. The Johnson–Lindenstrauss projection is still used in the paper, but for a different purpose: to prevent modulo wrap-around. We summarize the explicit norm constraints and the use of Johnson–Lindenstrauss projection for preventing modulo wrap-around below.
Individual witness vector norm constraints
Proving that ||\mathbf{s}_{i,1}||^2_2 + ||\mathbf{s}_{i,2}||^2_2 \leq \beta^2 is equivalent to proving that \beta^2 - ||\mathbf{s}_{i,1}||^2_2 - ||\mathbf{s}_{i,2}||^2_2 is non-negative.
Lagrange’s four-square theorem states that any non-negative integer can be written as the sum of four squares. Thus, we can find four integer \epsilon_{i,0}, \epsilon_{i,1}, \epsilon_{i,2}, \epsilon_{i,3} \in \mathbb{Z} such that:
The values \epsilon_{i,j} of the i-th signature are added to the witness as the coefficients of the polynomial
Note that having a polynomial \mathbf{a} = a_0 + a_1 X + ... + a_{d-1} X^{d-1}, we can compute its norm as (using the fact that ||\mathbf{a}||^2 = ct(\langle \mathbf{a}, \sigma_{-1}(\mathbf{a}) \rangle) for the conjugation automorphism \sigma_{-1} and X^d = -1):
We denote \mathbf{a}' = a_0 - a_{d-1} X - ... - a_1 X^{d-1}.
Now we can rewrite the norm constraint into the LaBRADOR constraint as:
But we also need to check that the new witness elements have been constructed correctly and that the coefficients of the witness elements are so small that they don’t wrap around q'.
Let’s observe how to express a constraint that the j-th coefficient of the polynomial \mathbf{a} is some value, let’s say b:
For each \epsilon_i we need to prepare constraints that ensure \epsilon_{i,4},..., \epsilon_{i, d-1} are zero.
We also need to ensure that \mathbf{s}'_{i,1} is constructed correctly from \mathbf{s}_{i,1}, for example:
Same for \mathbf{s}_{i,2} and \epsilon_i.
Contrary to the approach based on the sum of four squares, Dachshund uses base-2 decomposed vectors, which are multiplied by polynomials with boolean coefficients. There is probably not a significant difference in performance.
Preventing wrap-around
Following the aproach in the paper, it is necessary to ensure that wrap-around does not occur in the following two equations:
It turns out the first is more restrictive, we obtain:
From the second equation we obtain:
To ensure this holds, the Johnson–Lindenstrauss projection is used.
Issue 2: reshaping the witness
Another limitation of the Chihuahua frontend in the context of signature aggregation is its inefficiency when dealing with many witness vectors, due to the need to compute numerous so-called garbage polynomials.
The prover’s runtime—and how quickly LaBRADOR converges toward the base case (i.e., how many recursive steps are required to compress the proof size)—depends on two key parameters:
- the multiplicity r: the number of witness vectors
- the rank n: the number of polynomials in each witness vector
The paper proposes reshaping the witness to achieve a more balanced configuration, targeting r = O(\sqrt{N}) witness vectors of rank n = N, where N is the number of signatures.
Originally, the witness consists of r = 2N vectors (even more when exact norm constraints are added), each of rank n = 1. This is a highly unbalanced configuration. For LaBRADOR’s recursive compression to be efficient, it is preferable for r and n to be closer in magnitude. To address this, the scheme introduces a padding strategy: the witness is reshaped so that n \approx N and r \approx \sqrt{N}, with the new witness vectors padded with zeros as needed.
However, this issue is also addressed by the Dachshund frontend—Dachshund is designed to handle a large number of witness vectors efficiently.
Ring choice
Another aspect is the choice of the ring. While the paper analyzes several options, it ultimately adopts the same configuration as used in Lazer. Polynomials are multiplied modulo several small primes p_i (using NTT), and results are then combined using the explicit CRT modulo q. The use of small 16-bit primes p_i (between 2^{12} and 2^{14}) that fully split in \mathbb{Z}_r[X]/(X^{64} + 1) enables efficient Montgomery arithmetic (see the Greyhound paper for more).
Summary
The two approaches for signature aggregation—the one from the paper Aggregating Falcon Signatures with LaBRADOR and the Lazer approach—are quite similar, so we believe our benchmarks (based on the Lazer code) are relevant for both.
The most compelling feature of the benchmarked lattice-based signature aggregation scheme is its proof size, while the biggest obstacle to adoption may be the verification time. Verification performance could likely be improved using multi-threading techniques, though this requires further investigation. That said, improvements to both the LaBRADOR protocol and its C implementation are already underway by the LaBRADOR authors, and these are expected to speed up verification—though it’s currently difficult to quantify by how much.
While the verification time may improve with future optimizations, it likely cannot match the hash-based approach (see table below), where verification takes only a few milliseconds.
| Metric | LaBRADOR + Falcon (10000 sigs, 1 thread) | Hash-Based (8192 sigs, 4 threads) |
|---|---|---|
| Proof Size | 74.07 KB | 1.7 MB (targeting ~128 KB with optimization) |
| Proving Time | 5.95 s | 5 s |
| Verification Time | 2.65 s | 106 ms |
| PQ Security | Yes (lattice-based) | Yes (hash-based: Poseidon2 signature, Keccak in PCS merklization) |
| Parallelization | To be explored | Very good — 4 threads used; scales almost linearly up to 4, sublinearly but effectively beyond |
To conclude, the LaBRADOR scheme appears to be very well-suited to the specific constraints that arise in the aggregation of Falcon signatures. To improve verification time, exploring delegation techniques similar to Dory could be a promising direction.