MEV Auction: Auctioning transaction ordering rights as a solution to Miner Extractable Value

[karl]

Special thanks to Vitalik for much of this, Phil Daian as well (& his amazing research on MEV), Barry Whitehat for also coming up with this idea, and Ben Jones for the rest!

Blockchain miners (also known as validators, block producers, or aggregators) are nominally rewarded for their services by some combination of block rewards and transaction fees. However, being a block producer tasked with producing a particular block gives you a lot of power within the span of that block, letting you arbitrarily reorder transactions, insert your own transactions before or after other transactions, and delay transactions outright until the next block, and it turns out that there are a lot of ways that one can earn money from this. For example, one can front-run decentralized exchanges (both Uniswap-style and the order book variety), be the first to claim whistleblower rewards, have a favorable position in ICOs, as well as many other forms of mild manipulation of applications. Recent research shows that the revenue that can be extracted from this (called “miner-extractable value” or MEV) is potentially significantly higher than transaction fee revenue.

Frequent batch auctions are one traditional response to market manipulation by reordering. In an FBA, instead of processing transactions “as they come”, a market gathers all transactions submitted within the same time span (could be short eg. 100 ms, or a minute or longer), reorders them according to a standard algorithm that does not depend on order of submission, and then processes them in that new order. This makes micro-scale timing manipulation nearly irrelevant.

We propose a technique in a similar spirit to how FBAs remove micro-scale timing manipulation, with one major difference. In an FBA, there is only one application, and so there is one natural “optimal” order for transactions (orders): process them in order of price. In a general-purpose blockchain, there are many applications with arbitrary properties, and so coming up with a “correct” order is virtually impossible for a fixed algorithm. Instead, we simply auction off the right to reorder transactions within an N-block window to the highest bidder. That is, we create a MEV Auction (MEVA), in which the winner of the auction has the right to reorder submitted transactions and insert their own, as long as they do not delay any specific transaction by more than N blocks.

This creates a form of “managed centralization”: a single sophisticated party wins the auction and can capture all of the MEV. We call this party a “sequencer.” Having a single sequencer reduces the benefit to other block proposers of using “clever” algorithms to near-zero, thereby increasing the chance that “dumb” block proposers will be long-term viable and hence promoting decentralization at the block proposal layer. This technique can theoretically be used at layer 1, though we also show how it is a perfect fit for layer 2 systems, particularly systems such as Optimistic Rollup, zkRollup, or Plasma.

This mechanism is designed to extract MEV for the sole purpose of supporting our (inclusive) blockchain community. In fact, this mechanism could be the revenue stream for opt-in self governance built to fund the internet’s public goods. We mustn’t participate in an MEVA which funds things we don’t like!

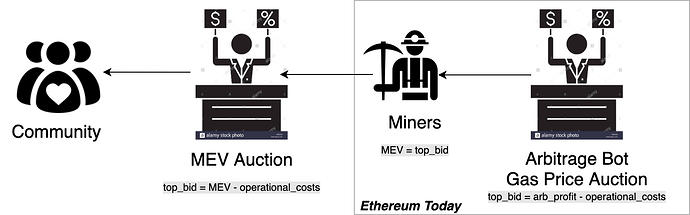
MEV Auction on top of Gas Price Auction

Control over transaction ordering has become extremely profitable especially as smart contracts like Uniswap have gained popularity. There have been multiple occasions where trades on Uniswap with high slippage caused tens of thousands of dollars in free arbitrage profits.

These arbitrage opportunities are taken advantage of by arbitrage bots that watch the blockchain and participate in the gas price auction. These bots outbid each other at high frequency as long as the price they pay for the transaction is not excess of the amount of money they stand to make. Frontrun.me has great information collected on these auctions happening in the background of Ethereum every day.

Counter-intuitively, the real winner of these auctions is Ethereum miners, as bots which outbid each other raise the gas price. This increased gas price increases miner fees and revenue. By introducing an MEV Auction in addition to this gas price auction we can employ the same market mechanism that extracts frontrunning fees to be directed at miners, and redirect that profit back to the community.

Implementing the Auction

The auction is able to extract MEV from miners by separating two functions which are often conflated: 1) Transaction inclusion; and 2) transaction ordering. In order to implement our MEVA we can define a role for each function. Block producers which determine transaction inclusion, and sequencers which determine transaction ordering.

Block producers // Transaction Inclusion

Block proposers are most analogous to traditional blockchain miners. It is critical that they preserve the censorship resistance that we see in blockchains today. However, instead of proposing blocks with an ordering, they simply propose a set of transactions to eventually be included before N blocks.

Sequencers // Transaction Ordering

Sequencers are elected by a smart contract managed auction run by the block producers called the MEVA contract. This auction assigns the right to sequence the last N transactions. If, within a timeout the sequencer has not submitted an ordering which is included by block proposers, a new sequencer is elected.

Sequencers and Instant Transaction Inclusion

In addition to extracting MEV, the MEVA provides the current sequencer the ability to provide instant cryptoeconomic guarantees on transaction inclusion. They do this by signing off on an ordering immediately after receiving a transaction from a user – even before it is sent to a block producer. If the sequencer equivocates and does not include the transaction at the index which they promised, the user may submit a fraud proof to the MEVA contract to slash the sequencer. As long as the sequencer stands to lose more than it can gain from an equivocation, we can expect the sequencer to provide realtime feed of blockchain state which can be monitored, providing, for instance, realtime price updates on Uniswap.

Implementation on Layer 2

It is possible to enshrine this MEVA contract directly on layer 1 (L1) blockchain consensus protocols. However, it is also possible to non-invasively add this mechanism in layer 2 (L2) and use it to manage Optimistic Rollup transaction ordering.

In layer 2, we simply repurpose L1 miners and utilize them as block proposers. We then implement the MEVA contract and designate a single sequencer at a time. (Note: Interestingly the single sequencer can also be run by a sub-consensus protocol if desired.)

In fact, using MEVA for layer 2 is a perfect fit as it allows us to permissionlessly experiment with different parameters for the auction while simultaneously realigning Ethereum incentives to direct revenue back into the ecosystem. This may serve as the primary revenue stream for blockchain self-sustenance.

Considerations

MEV Auction Collusion

One concern is auction collusion. Bidders colluding to reduce competition and keep the auction price artificially low breaks the ability to accurately discover and tax the MEV.

A mitigation is to simply increase the ease of entering the aggregation market by releasing open source sequencer software. This can help to establish a price floor because with low barriers of entry we can expect enough competition that there will be at least one honest sequencer bid.

Long term incentive alignment

The most naive way to implement MEVA is by holding a first-price auction once a day, giving the winner of the auction a monopoly on block production for that day. All proceeds raised by the auction are then sent into a public goods fund. Unfortunately, this approach has a serious problem: an attacker need only outbid the aggregation costs for a single time-slot in order to become the selected sequencer and degrade network quality.

Adding the equivalent of a security deposit for the sequencer goes a long way to help mitigating this problem. If the sequencer degrades network quality at any point during their slot, they should be penalized in proportion to the amount of harm they cause to the network. This can be implemented as a simple bond which can be slashed by a subjective judgement of misbehavior, or by locking up an asset which has a price correlated with the health of the network. Note that sequencer misbehavior can often come as a non-uniquely attributable fault and so unfortunately require subjective judgements to enforce.

The Parasitic L2 Problem

Layer 2 mining has gotten bad press for diverting revenue away from L1 miners who secure the network. Diverting revenue from L1 implicitly decreases the security budget, and thereby makes it less costly to perform 51% attacks.

While I wish there was a clear mitigation, in reality the parasitic L2 problem deserves much more research & risk analysis. It could be the case that L2 chains drive up demand for L1 enough to keep the price of ETH high, or ETH remains valuable because it is seen as money, or we simply use out-of-protocol means to protect our most critical blockchains. This remains to be seen and is a great area of research.

Path Forward

Designs like these are critical for framing the coming wave of Ethereum upgrades as not only innovations in scalability, but also as an opportunity to realign incentives to be pro-community, pro-commons, and pro-public goods. Without serious thought around how we will sustain blockchain technology we risk creating resilient decentralized architectures which eventually crumble due to massive economic centralization. This is not a future anyone wants to live in.

Thankfully, these designs show the possibility of encapsulating and reinvesting MEV back into the community. Further research and economic models will be key as we bring these systems into production. Let’s do it!

[lsankar4033]

whoa, unbundling inclusion from ordering is a cool idea!

How would you determine the bond that a sequencer is required to risk in the MEVA contract for a given future time window? It seems like it needs to be based on some prediction of MEV in the long-run?

[tchitra]

This sounds great and is a good starting point for formalizing a threat model for the MEVA. There are a few things that seem like major challenges for this system:

1. Added latency between transaction selection and sequencing
2. Constructing a Bayes-optimal auction for the sequencing auction that is efficiently computable
3. Inflation / dilution / burning mechanics of the underlying system
4. This doesn’t address all sources of MEV, so there is non-zero deadweight loss for the tax

Let’s analyze these independently.

---

Latency

It seems unavoidable that this mechanism adds in some latency between transaction selection and transaction sequencing. The simplest high-level view of the mempool is as a standard priority queue (implemented as a heap) whose keys are (gas price, nonce) [0]. This means that when a block is emitted from an honest and rational (profit-maximizing in-protocol only) miner, they simply pop the maximum number of transactions that fit into a block and pack a block [1]. This combines selection and sequencing in a single operation (with runtime O(n \log T) where n is the number of transactions in the mempool and n is the number withdrawn for a block) and doesn’t incur the latency of having two agents — the transaction selector and the transaction sequence — having to coordinate.

What are options for dealing with this latency? In particular, how do we minimize the rounds of communication between the transaction selector and the sequencer? I have a couple ideas:

• Mild Idea: Run the sequencer auctions ahead of the block production time (e.g. auction for block h takes place in a smart contract executed at block h-1) so that the winning sequencers are ready to receive transaction sets ahead of time. The sequencer might need to stake a small amount of collateral, to ensure that they are online to sequence when it is their turn
• Crazy idea: Have a distributed priority queue such that each potential sequencer participates in with some stake (e.g. they lock up some assets at block height h to commit to a sequence at height h+1). Each insertion or deletion into this priority queue costs a fee and the final ordering cost is the aggregation of these fees. This way, sequencer can spend the entire time between a block at height h and a block at height h+1 attempting to sequence transactions, such that once the transaction selector sends the approved transactions, the elements that aren’t in the queue are removed and the transactor who wins (either by auction or via the most fees, this might be a way of obviating the auction dynamics) chooses the final ordering of the transactions that were selected that weren’t in the distributed priority queue. This optimization doesn’t improve the worst case run time, but it does improve the average case run time. There is some potential for griefing attacks, but they are bounded by how unbalanced the heap implementation can get

---

Optimizing the Auction
The field of combinatorial auctions has been well-studied by game theorists such as Noam Nisan and Tim Roughgarden for an extended period of time. Most combinatorial auctions, such as the spectrum auction, involve selling unordered sets, so these techniques (see Chapter 11 of Nisan, Roughgarden, and Tardos) should make it relative easy for the transaction selection auction. I wouldn’t try to reinvent the wheel here, if I were you.

On the other hand, auction dynamics for the sequencing side of things is much harder to discern. In a famous paper, Betting on Permutations illustrates a Condorcet-like impossibility result — it is NP-hard to compute an optimal betting / auction strategy when bidding on permutations. One of the reasons for this is that the original first-price auction for gas prices, in isolation of previous blocks and mempools, is not a Bayes-optimal auction, whereas this auction is. The reason for this is that bidders have to condition their expected utility computations on the transactions they have received. How do we analyze such an auction in a way that is comparable to how the current gas auctions works? We’ll try to walk through the basic mathematical elements that each agent has to choose and then provide some tried and trued techniques for doing primitive mechanism design here.

In order to do this, we first have to define fairness. Note that we consider an auction to be \epsilon-fair if the probability distribution over auction outcomes returns no particular ordering with probability \epsilon more than the uniform distribution (e.g. all orderings are basically equally likely). Why is this a good definition fair? It serves as way of saying that no particular transaction ordering is favored by much under all possible instantiations of the auction with different participants.

Next, we need to look at what it means for an individual participant or agent to pick a certain ordering. Let’s suppose that the transaction selector has sent n transactions, T_1, \ldots, T_n \in \mathcal{T} and that the transaction sequencer has a utility function U : \mathcal{T}^n \rightarrow \mathbb{R}. We will represent the possible transaction orderings (e.g. linear orderings such as T_1 < T_3 < T_2) via permutations on n letters. In order to figure out our bidding strategy, we first have to compute a) which permutations are most important to evaluate (there are n! of them, so we need to be efficient) and b) how to value a given permutation. The first is specified by computing a subjective probability, \mu_{n}(\sigma) = \mathsf{Pr}[\sigma(T_1, \ldots, T_n) | n, T_1, \ldots, T_n] for each element \sigma \in S_n, where S_n is the symmetric group on n letters. The second component is specified by an expected utility,

\mathsf{E}[U | T_1, \ldots, T_n] = \frac{1}{n!} \sum_{\sigma \in S_n} U(\sigma(T_1, \ldots, T_n))\mathsf{Pr}[\sigma(T_1, \ldots, T_n) | n, T_1, \ldots, T_n]

Finally note that in this notation, we define a \epsilon-fair auction as one that returns a transaction ordering \sigma(T_1, \ldots, T_n) with probability distribution p where d_{TV}(p, \mathsf{Unif}([n])) < \epsilon.

Each rational participant in the auction will have a utility function U and subjective probabilities \mu_n that will guide how their strategies evolve in this auction. If we believe that rational, honest players are participating in the sequencer protocol, then we rely on this expectation being positive (altruists are those who continue playing when this is non-positive). Moreover, there isn’t a unique archetype of a rational, honest player here (unlike in consensus) — for instance, we have two simple strategies that meet the stated goals of being rational, non-malicious, and able to always submit a bid:

• Maximum a posteriori optimizer — select the ordering \sigma^* \in S_n such that \sigma^* \in \text{arg}\max_{\sigma \in S_n} \mathsf{Pr}[\sigma(T_1, \ldots, T_n) | n, T_1, \ldots, T_n]
• Empirical expected utility maximizer — Take k samples \sigma_1, \ldots, \sigma_k \sim \mathsf{Pr}[\sigma(T_1, \ldots, T_n) | n, T_1, \ldots, T_n] and choose the ordering \sigma^* = \text{arg}\max_{i \in [k]} U(\sigma_i(T_1, \ldots, T_n)

These are only two of the rational, honest strategies available here as agents can localize their bets (e.g. convolve their subjective probability with the indicator function 1_{A}) to any subset A \subset S_n. This vastly expanded space of rational, honest strategies makes traditional algorithmic game theory tools somewhat meaningless for analyzing such an auction. What can we do?

We can take a page out of the online advertising auction design playbook and try to model the sequencing auction by segmenting the the participants into two categories:

• “Passive” honest, rational agents who participate regardless and have a static strategy and a single, common utility function U
• “Active” aggressive strategies that have dynamic strategies such that the probability measure \mu_n changes from block to block.

Once we do this, we can take techniques like those used in the above Milgrom paper to create auctions that have a social welfare function [2] V(\gamma) = \gamma V_{\text{passive}} + V_{\text{active}} whose revenue sharing and reserve pricing can be optimized based on the desired goals of the sequencing auction. I strongly suspect this will be important in ensuring that spamming and spoofing these auctions is expensive for those who are trying to encourage participation in certain transaction orderings.

Note that methodologies for auctions, akin to the Milgrom paper, are inclusive of collusion — the authors do not assume independence of the bids that participants that are “active”. The parameter \gamma (as well as other parameters, such as reserve sizes) control how much correlation/bribery is needed to change an auction from the default.

This is all of the background needed to try to construct a k th price auction with reserve amounts that is \epsilon-fair. Good luck!

---

Impact on Inflation

If the fees from this auction are paid back to the network we have three options:

• Pro-rata redistribution: This is basically stake-weighted redistribution of the auction revenue
• Burned: We burn the revenue from the auction
• Concentrated redistribution: Only redistributing to certain participants (e.g. validators, top-k validators)

The third option is likely the most unfair and has perverse incentives to bribe validators for certain orderings. The second option has implications for inflation: If the MEV auction clearing prices are increasing faster than the block reward is increasing (e.g. subsidy inflation), then the ‘real’ inflation of the system will actually be lower than expected. The first option will cause a tax liability for holders and/or encourages the highest stake participants to try to cause the clearing price to increase. These trade-offs are really worth considering!

---

Other Sources of MEV

The simplest form of MEV that isn’t discussed is transaction elision — e.g. a validator not repeatedly adding a transaction to the transaction set. Under the assumption of 50% honest, rational agents, one can show that a transaction that enters the mempool at block h will eventually get into the chain at block h+k (there is a Kiayias paper for this that is escaping me). The probability that this happens decays exponentially in k (the exponential base is a function of the percentage of rational honest agents), but it does have a burn in time (e.g. linear for 0 \leq k \leq k', exponential for k \geq k').

---

Thanks to Brock Elmore, Peteris Erins, and Lev Livnev for useful discussion on these points

---

[0] In the current implementation of the Geth mempool, the file core/tx_pool.go contains the logic for the pool (including the priority queue). The choice of keys and comparison is actually done in a different translation unit, miner/worker.go

[1] Note that Bitcoin’s mempool logic is significantly more complex and sophisticated. The child-pays-for-parent tree allows for UTXOs to be spent over multiple blocks and lets scripts trigger future payments. See Alex Morcos excellent fee guide and Jeremy Rubin’s OP_CTV. It should be noted that this complexity in the mempool is partially due to the inflexibility of Bitcoin script, which forces multiblock payments to be mediated at the mempool (instead of in a contract). But it has the side-effect of making fee sniping a lot more difficult in Bitcoin.

[2] Recall that in Algorithmic Game Theory, the social welfare function represents the ‘macroeconomic’ observable that we are trying to optimize for our mechanism. In auctions with independent bidding and no repeated rounds or reserves, this simply is the sum of the quasilinear utilities of the participants. When there is collusion / correlation, this gets significantly more complciated

[vbuterin]

Optimizing the Auction

Are you assuming here that the sequencing auction for block N happens after the transactions in block N are known? I think what @karl had in mind was the sequencing auction happening well before block N, eg. potentially even a day before. This way the sequencers would be buying rights to the expectation of future MEV, not bidding on permutations (and insertions and delay-to-next-block operations) directly. Does this simplify the above analysis?

Impact on Inflation

The third option has a lot of internal choice! One option that I am particularly excited about is funding public goods through some DAO, on-chain quadratic funding gadget, or similar tool.

he simplest form of MEV that isn’t discussed is transaction elision — e.g. a validator not repeatedly adding a transaction to the transaction set.

I agree this is a form of MEV too! Though I wonder how much of that is captured by the ability to reorder transactions arbitrarily including inserting your own transactions before some of the transactions in the original block.

[jannikluhn]

Interesting!

The general idea seems to be to redistribute MEV from miners to some other entity, e.g. a DAO which funds public goods. Wouldn’t this basically be equivalent to leaving the MEV to miners, but instead send an equal fraction of block rewards to the DAO?

Sequencers and Instant Transaction Inclusion

The sequencer can only commit on a specific position in a block, not that the transaction will be included at all, no? I guess usually they can predict this fairly accurately, but there’s still a chance that they are wrong (especially if the producer actively refuses to include a specific transaction).

[vbuterin]

Wouldn’t this basically be equivalent to leaving the MEV to miners, but instead send an equal fraction of block rewards to the DAO?

No, because it’s not just about long-run average returns, it’s also about incentives. This technique removes the incentive of trying to collect MEV from miners, and gives the incentive to the centralized party that won the auction. This way the auction participants “absorb” the gains from sophistication, making it more plausible that miners/block producers will remain decentralized as they can safely be dumber.

[valentin]

@tchitra

What are options for dealing with this latency? In particular, how do we minimize the rounds of communication between the transaction selector and the sequencer?

This could be a significant problem indeed as it makes block mining a distributed computation between 2 parties. Can this be mitigated by putting the sequencing algorithm into a contract, which the block producers need to follow? Each sequencer will participate in the auction with (sequencing code, bid) pairs. Once the winner is known, the block producers need to obey the current sequencing code.

One downside of this approach is a potential DoS attack against the block producer, by submitting the ordering code, which is artificially complex to execute.

On the plus side, this eliminates the need for communication between 2 parties to mine a block.

[wjmelements]

Hello, I am in the business of MEV. There are some good ideas in this proposal. I have a critique and alternative proposals. Some things you say aren’t true but I won’t go into too much detail because a lot of the game is a well-kept secret.

Transaction ordering is powerful because it determines which transactions succeed and which fail, and also what happens should they succeed. Miners have dictatorial power over this $10m+/year market because there are no rules regarding transaction ordering. Even if there were rules miners still win by excluding transactions.

Block proposers are most analogous to traditional blockchain miners. It is critical that they preserve the censorship resistance that we see in blockchains today

Proposers are still incentivized to exclude transactions. You introduce another source of censorship: independent reordering. Separating these powers is an improvement but the sequencer, the producer, and the transactors could still be the same party, and the sequencer could have conflicts of interest outside of the block.

This auction assigns the right to sequence the last N transactions.

Changing the order of transactions impacts state. This would substantially increase the effective confirmation time leading to instability and a higher rate of reverted transactions.

It also impacts gas usage. If a block proposer only selects the transactions but does not order them, there can be no block gas limit. It is nontrivial to prove that a set of transactions cannot be ordered below a given gas threshold. Using transaction gas limits is sufficient but you end up with barren blocks and substantial gas-usage volatility; the network would be massively under-utilized. A related concern is that the sequencer doesn’t care how much gas is used.

If, within a timeout the sequencer has not submitted an ordering which is included by block proposers, a new sequencer is elected.

This process could last an unbounded amount of time. Block proposers could have incentivizes to exclude the ordering. Moreover the ordering itself could be reverted by a future reordering. Instead you could have a hash of the ordering be part of the bid itself, since the MEV is known at the time of the bid.

In addition to extracting MEV, the MEVA provides the current sequencer the ability to provide instant cryptoeconomic guarantees on transaction inclusion. They do this by signing off on an ordering immediately after receiving a transaction from a user – even before it is sent to a block producer.

I don’t see a reason for the sequencer to do this. An index is not a strong guarantee either. You could even withhold such a proof until you actually provide the sequence.

As long as the sequencer stands to lose more than it can gain from an equivocation, we can expect the sequencer to provide realtime feed of blockchain state which can be monitored, providing, for instance, realtime price updates on Uniswap.

They don’t have to provide this information to the public in realtime.

Bidders colluding to reduce competition and keep the auction price artificially low breaks the ability to accurately discover and tax the MEV.

Collusion requires barriers to entry. You create a barrier to entry by incentivizing the probable-winner to submit more MEV transactions and punishing their competitors for losing. Once you start winning you will probably keep winning indefinitely.

This can help to establish a price floor because with low barriers of entry we can expect enough competition that there will be at least one honest sequencer bid.

Sequence bidding is not free.

Proposals

MEV is potentially significantly higher than transaction fee revenue.

MEV is the true block reward. Gradually diminish the inflationary block reward instead of trying to tax MEV. Let “dumb” block producers maintain viability via open-source software. Preserve confirmation time.

Define a standard transaction ordering algorithm to increase the cost of censorship.

Ban or punish inclusion of transactions that would revert at the top-level. These waste shared computational resources anyway. Preventing block producers from winning revert rewards removes a barrier to entry and reduces the power of the block producer. Let block producers manage revert-DOS off-chain.

[adlerjohn]

@wjmelements

Ban or punish inclusion of transactions that would revert at the top-level.

Making reverting transactions invalid is non-trivial. If you receive an unconfirmed transaction from a peer and validate it locally, whether it reverts or not depends on when it’s executed (i.e. its index in the totally ordered list of transactions provided by the blockchain). Therefore you can’t ban a peer that sends you a reverting transaction (unless you make the peer provide you the complete ordering of transactions it used to execute that transaction, but that’s computationally infeasible). Being unable to ban a peer that sends you an invalid transaction is a DoS vector.

Note that this does not apply in the same way for spending conditions with monotonic validity, such as the predicates used in Bitcoin Script or those that have been proposed for Fuel.

@wjmelements

Define a standard transaction ordering algorithm

A standard transaction ordering algorithm might help with the above, but I’m not aware of even a single one that has been proposed that isn’t hopelessly broken.

[Pratyush]

This recent paper might be relevant: it separates transaction ordering from transaction execution at the consensus layer.

[jaybny]

FYI - we came up with these same ideas in 2018 - see here: https://medium.com/@jaybny/on-dex-fac434d7730f

[karl]

@jaybny This is really cool! Did you come up with any fun takeaways/analysis since your first post?

[jaybny]

thanks Karl. I have lots of ideas and directions on where to go with this… but am not a fan on working on top of Eth, although I love the tech and community.

I actually received a patent for some of this, and am looking to build a DEX proof-of-concept.

[yaronvel]

We are working on something somewhat similar in application level. We decided to first tackle the lending platforms liquidation MEV. Where liquidators compete on a well defined premium, which give rise to gas wars and millions of $ that goes to miners.

Our approach is to make the liquidators auction in the beginning of the month for the right to liquidate. And then to divide the liquidations fairly among the liquidators over the month.
We are implementing a practical approach that will go live on September atop makerdao. The idea is that liquidators will share their profits with the users, who in return give them priority in the liquidations.
A defi-lego trick makes it possible to achieve it without any change in makerdao protocol.

More details are available here: https://medium.com/b-protocol/b-protocol-b6dd4e3bf9c0

[kladkogex]

There is a faster alternative. We are implementing it in our project and it could be easily implemented in ETH2 or any other finalizing blockchain.

• Transactions are submitted encrypted using threshold encryption.

• A committee (say ETH2 committee) collectively holds the decryption key.

• Once the block proposer includes the transaction into the block, and once the block is finalized, the committee decrypts the transaction (the committee only needs to decrypt the symmetric key that encrypts the transaction).

• Once the transaction is decrypted, EVM runs on it.

Thats it - it solves all the problems. You can run Uniswap on it with zero front running.

There are some technicalities (for instance gas price, nonce and some other things need to be submitted unencrypted). But they are all workable. Note that this could be implemented at the application level too.

[ratacat]

A committee (say ETH2 committee) collectively holds the decryption key.

What happens if the key is lost? Maybe I don’t understand how large the committee is…seems like maybe a pretty central point of failure

[samueldashadrach]

What is the purpose of this?

Why is maximising MEV extracted a goal? It’s going to happen anyways, why do we want to speed this up? Intellectual curiosity? Market efficiency?

Is any part of this proposal going to be added to the ethereum spec? Or is it all features being built on top of it (via a DAO or something)?

[pmcgoohan]

I posted about similar issues soon after the ETH ICO (nothing like as rigorous as the Flash Boys 2.0 paper of course).

r/ethereum - Miners Frontrunning

I’m glad the community is taking these issues so seriously.

It’s a noble idea to accept the MEV losses but redirect them to the commons, but I’m not sure it protects the unsophisticated and under-resourced from the sophisticated and resourced as is.

Consider 3 participants (A,B,C)…

A - calculates that winning the MEV auction for tomorrow is worth 1 ETH in costs because they will likely make 0.1 (after costs) from their trading if they can frontrun, and only 0.05 ETH if they can’t
B - calculates that winning the auction is worth 0.5 ETH in costs because they will likely make 0.1 (after costs) if they can frontrun, and only 0.08 if they can’t
C - just wants to trade and has no idea that MEV auctions even exist

So the outcomes for the A/B sophisticates and the naive C are…

A - wins the auction in this case, and has to pay 1 ETH, but makes 0.1 so is happy
B - loses the auction, but also knows that they have, and therefore avoids trades that they can’t profit from. They make their 0.08 without the overhead of winning the MEV
C - has absolutely no idea that any of this has taken place. They get frontrun continually all day and are none the wiser. Effectively, the 1 ETH paid by A is extracted exclusively from C, the actor we are trying to protect.

“This technique removes the incentive of trying to collect MEV from miners, and gives the incentive to the centralized party that won the auction”
If we’re not careful, this will have achieved nothing. The same bad actors that would have been miners have become MEV auction participants instead, just with a different name.

I think the auction proceeds at least need to be distributed proportionately to all the participants in blocks sequenced by the auction winner (except for themselves), not just some common DAO like fund. In this outcome:

A - pays B and C equally
B - will know they are going to get paid by A and will include that in their expected win calculations
C - will have no idea whats going on, but will be happy to get some compensation (and statistically the set of unsophisticated Cs will not lose out, although individual Cs may lose big)

But really, I’m not sure the focus should be on sequencing. Block production is the weak point as this is where transactions can be censored and frontrun.
Once you have a fair block, sequencing is a non-problem. The fairest method is always to treat all transactions in a block as if they were simultaneous. This could even just be done as a matter of convention in smart contracts. If we are talking about many blocks per second, there is no real downside to this.

So in summary, I think the focus needs to be put back on a fair consensus driven block proposal. Sequencing is a distraction.

[Mister-Meeseeks]

Just to be clear, this would result in significantly more front-running. Yes, maybe the profits would go to a worthier cause, but the average Dex trader would experience much worse slippage.

Right now existing arbitrage bots don’t exploit every opportunity to the max, because there’s execution risk. There’s all kinds of reasons an attempted front-run order might fail, if another bidder wins the auction, if the target is mined before the sandwich propagates, or even if the target cancels their transaction. If that happens the front-runner still pays gas on the “empty transaction”, and possibly even gets filled at unprofitable prices. Many exploitable target slip past, because the bots don’t think the risk is justified.

In contrast, the sequencer would know with 100% certainty, and therefore would exploit every single opportunity, extracting the maximum amount each and every time. More so, the sequencer would have even worse exploits at his disposal. There’s a lot of exploitation opportunity during periods of turbulent trading, when many trades on the same pool occur in the same block, like ICOs.

These happen to be the time that ordinary traders set the highest slippage. Front-runners can tactically insert their own transactions, but they can’t re-arrange third party transactions. The sequencer’s arbitrary ability to re-sequence introduces very large potential attacks in these instances. For example if the normal sequence is Buy->Buy->Sell->Sell, the sequencer could re-arrange to Buy->Sell->Buy->Sell, which lets them front-run twice as much value. Technically miners could do the same, but in practice 95%+ don’t, because running a mining rig requires different core competencies than being an arbitrage trader.

Finally, the two-phase commit nature of the process gives the sequencer a free option. This is equivalent to “last look” that you see in certain traditional markets like FX. The sequencer has N blocks to declare the sequence. He could include two of his own trades in the block- one to buy ETH/USD and one to sell ETH/USD, with the caveat that the first trade cancels the second. If the price of ETH rises in the next N blocks, he sequences it so that he buys ETH/USD. If it falls, he sells ETH/USD. Front running only extracts value from liquidity takers. But this would impose a persistent cost to Dex liquidity providers.

[pmcgoohan]

@Mister-Meeseeks

Just to be clear, this would result in significantly more front-running

This post is absolutely bang on. Arbitrage risk is a huge deterrent in itself. I say this as an arber myself in other non-crypto markets. Anything which reduced that risk to zero would allow me to put x5 the volume on I otherwise would at the direct expense of other participants.