MEV-resistant ZK-Rollups with Practical VDE (PVDE)

Layer 2
,
1

MEV-resistant ZK-Rollups with Practical VDE (PVDE)

@zeroknight , @0xTariz , and @radzin from Radius.xyz

Abstract

Current MEV solutions based on time-lock puzzles are not viable. Operators cannot easily detect invalid time-lock puzzles or transactions, which can even lead to DoS attacks. We are designing an MEV-resistant ZK-Rollup with a practical approach to MEV minimization using Practical Verifiable Delay Encryption (PVDE). This method generates zk proofs within 5 seconds, a validity proof needed to prove that solving the time-lock puzzles will lead to the correct decryption of valid transactions.

Background & Motivation

Decentralization Is Disguised

The structure of a blockchain is fully decentralized, but the content of each block is not.

MEV attacks occur from revealed transaction data and the centralization of miners who see the contents of block transactions and decide which transactions are included in a block. By leveraging their power to censor and reorder block transactions, miners can perform front-running, back-running, or sandwiching attacks to extract profit from users. The problem is that most users are unaware of being the victim of these malicious attacks.

In L1, block-building competitions among miners of different blockchains and high gas fees can prevent MEV exploitations from miners/attackers. Proposer/Builder Separation (PBS) is another proposed solution for MEVs in L1s, but usersā€™ assets are still prone to attacks as MEV opportunities are still publicized in a decentralized way.

In L2s, the case is a bit different. If the operator correctly computes the state transitions and includes only valid transactions, it becomes difficult to detect the censorships or intentional reorderings as only the computational integrity is verified. This creates a debate to the centralization/decentralization dichotomy. Due to the limited nature of blockchain scalability, L2 needs to maintain a small number of operators for its scalability which allows more room for operators to extract MEV profit. Additionally, lower gas fees on L2s attract mempool searchers (attackers) to MEV attacks.

We must assume that operators work in a permissionless manner to ensure a transparent and safe L2 ecosystem. A grounded approach that prevents the manipulation of blocks by the centralized operators in L2 is therefore needed. If there is no inherent solution to control the significant power of operators,

The adoption of layer 2 scaling solutions could represent the centralization of control over assets stored within them. ā€” barryWhiteHat

MEV auctions were proposed as a scheme to decentralize the operators. But as barryWhiteHat mentions, we need to be more cautious in the way we elect the operators through consensus mechanisms or with economical schemes like PBS as the security of L2s might very well be served. To prevent the usersā€™ assets from being exposed to MEV profits, we propose a complete privacy method for MEV minimization.

Time-lock Puzzle

Our MEV-resistant L2 solution ensures complete privacy of transactions as it reveals the contents of the transaction only after the transaction order is determined by the operator. We achieve this by encrypting the transactions temporarily based on time-lock puzzle. This scheme delays the time for the operator to find the symmetric key used to decrypt the transaction.

[Create and Encrypt Time-lock Puzzle]

The trader generates a time-lock puzzle that finds the symmetric key, then encrypts the transaction using the symmetric key.

  1. Create time-lock puzzle
    1. Generate a modulus: N = p*q
    2. Select generator: g\in G, \ \ where\ \ G \ \ is \ \ RSA \ \ group
    3. Compute symmetric key: S_K = g^{2^T} \ \ mod \ \ N
  2. Encrypt transaction

    1. Generate a symmetric key on an elliptic curve

      k = (k_0, k_1) \leftarrow JubJubAffine(S_K) \in F^2_q

    2. Encrypt message with Poseidon encryption scheme: C_{TX} = ENC(k, TX)

[Solve and Decrypt Time-lock Puzzle]

The operator receives the time-lock puzzle from the trader and solves it to find the symmetric key, then decrypts the transaction using the symmetric key.

  1. Solve time-lock puzzle
    1. Receive public parameter: N, T
    2. Compute symmetric key: S_K = g^{2^T} \ \ mod \ \ N
  2. Decrypt cipher text

    1. Generate a symmetric key on an elliptic curve

      k = (k_0, k_1) \leftarrow JubJubAffine(S_K) \in F^2_q

    2. Decrypt message with Poseidon encryption scheme: TX = DEC(C_{TX}, k)

Practical Verifiable Delay Encryption (PVDE)

Time lock puzzle schemes require large computational resources from operators. If a trader sends an invalid puzzle to the operator, resources are largely and meaninglessly wasted which can also lead to DoS attacks by malicious traders.

To prevent this, the trader must generate a zk proof to prove the integrity of the time-lock puzzle before the operator solves the puzzle.

The traderā€™s statement is as follows:

\pi_{PVDE}: The output value (also the symmetric key used for the decryption of the encrypted transaction) is found by computing the time-lock puzzle $2^t$times

The circuit must include the two computations to prove the statement:

  1. Time-lock puzzle: g^{2^{T}} mod \ \ N = S_K
  2. Poseidon Encryption: ENC(TX, S_K) ā†’ C_{TX}

It is difficult to solve the current RSA-based naive time-lock puzzle inside the zk circuit. For the past few months, we have been working to find a solution to the RSA sequential computation inside the zk circuit, with the help of Ethereum Foundation. To do this, we designed a total of 4 circuit computations and measured the proof generation time.

Our Practical Verifiable Delay Encryption (PVDE) method successfully generates the zk proof for the RSA-based time-lock puzzle within 5 seconds. This is an applicable and practical approach to generating the proof, which proves that solving the time-lock puzzle will lead to the correct decryption of valid transactions.

See the results of the experiment below. A more detailed experiment methods and results with the algorithm will be revealed on ethresear.ch.

Many thanks to @barryWhiteHat and @Wanseob-Lim from Ethereum Foundation

Spec

  • CPU: 2-way E5-2683 v4 (2.1GHz, 16-core)
  • RAM: 64 GB
  • Storage: 512 GB (SSD)

1
1898Ɨ106 10.3 KB

Circuit design (RSA: 2048 bits, T: 32678)
(When T is set to 32678, the operator solves the time-lock puzzle g^{2^T} in 7 to 8 seconds.)

  1. Naive time-lock puzzle
    1. Proving time: N/A
    2. Scheme
      1. g^{2^{T}} mod \ \ N = S_K
  2. Trapdoor time-lock puzzle
    1. Proving time: N/A
    2. Scheme
      1. Select random prime number p,q
      2. Compute trapdoor \phi(N) = (p-1)(q-1)
      3. 2^T \ \ mod \ \ \phi(N) = r
      4. g^r \mod \ \ N = S_K
  3. Efficient time-lock puzzle (our new scheme)
    1. Proving time: 540 secs
    2. Scheme
      1. generate parameters via a trusted setup : (g, g^{2^T})
      2. choose a random secret s (128 bits)
      3. generate inputs for zk-SNARKs (s_1, s_2) \leftarrow (g^s,(g^{2^T})^s)
        1. s_2 is used as a symmetric key and can be obtained via (s_1)^{2^T}
      4. generate a validity proof \pi \leftarrow \Pi.prove(g, g^{2^T}, s_1; s, s_2)
      5. verify the proof r \leftarrow \Pi.verify(\pi, g, g^{2^T}, s_1)
      6. obtain the symmetric key via time lock puzzle : (s_1)^{2^T} = S_K
  4. PVDE (our new scheme)
    1. Proving time: 5 secs
    2. Scheme: Combined zk-SNARK and sigma protocol

Participants

We design a ZK-Rollup solution to MEV exploitations caused by the centralization of operators producing the contents of the block and prevent the tradersā€™ transactions and assets from being exposed to the attackers.

Trader

Traders are parties that generate and execute L2 transactions.

To prevent assets from being exposed to the operators, the trader encrypts the transaction, then sends the time-lock puzzle, encrypted transaction, and zk proof to the operator.

  1. Generate a transaction
  2. Encrypt the transaction with the symmetric key generated with the time-lock puzzle
  3. Generate a zk-SNARK proof to verify the integrity of the time-lock puzzle and the encrypted transaction
  4. Send the time-lock puzzle, encrypted transaction, and zk proof to the operator

Operator

Operators are parties that collect and execute L2 transactions.

Operators can censor and intentionally reorder the tradersā€™ transactions to extract additional profit for themselves. To prevent these malicious MEV activities, operators must determine the block transaction order and send the corresponding commitment to the trader before they can decrypt the transactions and see the contents.

  1. Verify that the traderā€™s time-lock puzzle is valid
  2. Start solving the time-lock puzzle to find the symmetric key (sequentially compute 2^T)
  3. At the same time, determine the block transaction order and send the corresponding commitment to the trader. This should be completed before solving the time-lock puzzle
  4. Decrypt the transaction using the symmetric key and execute the transactions in the commitment

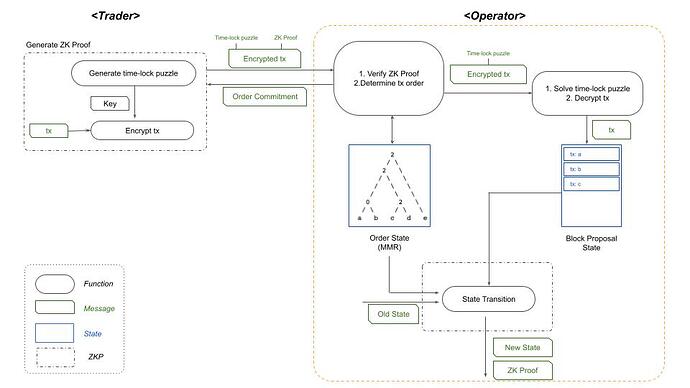
Architecture

2
2960Ɨ540 41.9 KB

Phase 1. Trader Generates Puzzle

  1. Generate a transaction
  2. Generate symmetric key with time-lock puzzle, encrypt the transaction, then generate validity proofs for the puzzle
    1. Setup(Ī›) ā†’ pp = (g, N, T)
    2. Generate_puzzle(pp, TX) ā†’ (ENC_{tx}, \pi_{PVDE})

      1. Time-lock_puzzle(pp) ā†’ S_K

        S_K = g^{2^T} \ \ mod \ \ N

      2. Encryption(S_K, TX) ā†’ C_{TX}

        C_{TX} = ENC(S_K, TX)

      3. Generate_proof(pp,TX) ā†’ \pi_{PVDE}

  3. Trader sends the following to the operator:
    1. Public parameters of time-lock puzzle
    2. Encrypted transaction: C_{TX}
    3. Transaction hash value: Hash(TX)
    4. \pi_{PVDE}

Phase 2. Operator Determines Transaction Order

  1. Trader verifies the validity of time-lock puzzle. If true, go to step 2.
    1. Verify(\pi_{PVDE}) ā†’ {True, False}
  2. Operator starts computing Timelock_puzzle to find the symmetric key for the decryption of the transaction
    1. Timelock_puzzle(pp)
  3. Determine the order of the transaction using Merkle Mountain Range(MMR) and send the commitment with order to the trader
    1. MMR(Hash(TX)) \rightarrow Commit(order, Hash(TX), merkle \_\ root, merkle\_\ path)

Phase 3. Trader Confirms Order

  1. Trader receives the commitments and checks the order of the transaction, then confirms that the time to receive the commitment was less than the minimum time-lock puzzle computation time
    1. Confirm that the transaction is included in Commit(order, Hash(TX), merkle \_\ root, merkle\_\ path)
    2. Check: T_{response} - T_{order} < āˆ†
      1. T_{response}: Total time for trader to send the encrypted tx and receive the commitment from the operator
      2. T_{order}: Expected time for the operator to determine the order and send the commitment to the trader
      3. āˆ† = Total time to solve the time-lock puzzle

Phase 4. Operator Decrypts Transaction and Executes

  1. Operator solves the symmetric key with time-lock puzzle and decrypts the transaction

    1. Solve_puzzle(pp, C_{TX}) ā†’ TX

      1. Timelock_puzzle(pp) ā†’ S_K

        S_K = g^{2^T} \ \ mod \ \ N

      2. Decryption(N, ENC_{tx}, S_K) ā†’ TX

        TX = DEX(C_{TX}, S_K)

    2. Transactions are executed in the order determined by MMR

Open For Discussion

The problem of MEV is the centralization of operators: the traderā€™s transactions and assets are pre-exposed to the operators in L2s. And as stated above, it is not possible to detect the censorships and intentional reorderings of transactions in L1s.

Our architecture is designed so that operators produce the block contents with encrypted transactions to prevent the tradersā€™ transactions and assets from being pre-exposed. The operators then need to send the finalized transaction commitments to the traders. Traders can challenge operators that did not execute the finalized order of transactions.

Our team is also discussing ideas to verify the true fairness of operators on L1 - weā€™d be happy to discuss this with the ethresear.ch community!

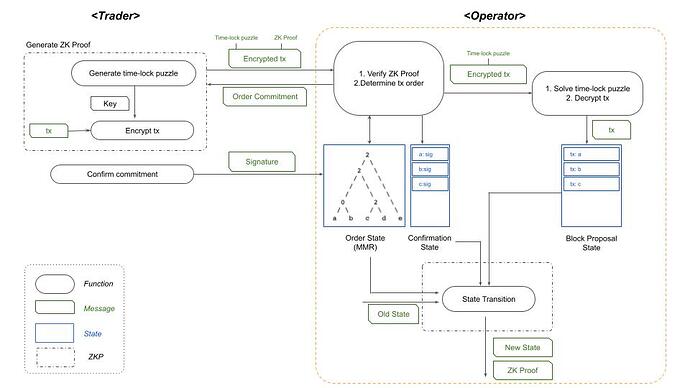
Order Commitment Validity

3
3960Ɨ540 46.3 KB

Order commitment validity ensures the L1 verifier contract validates that the operator executed the transactions in the determined order and finalizes the state without any challenges from the trader.

  1. Trader checks the order of the transactions in the commitments and confirms that the time to send the commitment was less than the minimum time-lock puzzle computation time
    1. Use membership proof to check that the traderā€™s transaction is included in Commit(order, Hash(TX), merkle \_\ root, merkle\_\ path)
    2. Check: T_{response} - T_{order} < āˆ†
      1. T_{response}: Total time for trader to send the encrypted tx and receive the commitment from the operator
      2. T_{order}: Expected time for the operator to determine the order and send the commitment to the trader
      3. āˆ† = Total time to solve the time-lock puzzle
  2. Send signature to operator: Sig(Commit(order, Hash(TX), merkle \_\ root, merkle\_\ path)
  3. Operator collects traderā€™s signatures and generates confirmation state in the order response time
  4. Operator solves the time-lock puzzle and decrypts the transaction, then collects the transactions by the order and generates block proposal state

    1. Solve_puzzle(pp, C_{TX}) ā†’ TX

      1. Timelock_puzzle(pp) ā†’ S_K

        S_K = g^{2^T} \ \ mod \ \ N

      2. Decryption(N, ENC_{tx}, S_K) ā†’ TX

        TX = DEX(C_{TX}, S_K)

    2. Block proposal state: TX, Commit(order, Hash(TX), merkle \_\ root, merkle\_\ path)

  5. Operator executes the decrypted transaction and generates zk proof to validate computational integrity on L1. Check the following two conditions in the circuit when generating zk proof:
    1. Confirm transaction validity
    2. Confirm that both order and Hash(TX) in both confirmation state and block proposal state are same
  6. When the state transition is complete, operator sends the new state and the validity proof to L1 verifier contract
  7. L1 verifier contract validates the computational integrity and order integrity using the validity proof and finalizes the state

Conclusion

MEV results in huge financial losses for traders. Thus, a solution to MEV minimization is imperative at current state. Our PVDE scheme is a practical approach to encrypt transactions using time-lock puzzles, so that operators do not waste any computational resources that lead to DoS attacks. The MEV-resistant ZK-rollup solution will fully prevent MEV attacks using cryptographic methods and eliminate the centralization of operators to provide a fair and efficient trading environment.

13 Likes
2

This is perhaps a naive question, and Iā€™ll admit I didnā€™t read this whole document, but is it possible to have multiple transactions from multiple parties encrypted such that they can be decrypted using a single VDF output? The idea here would be that block producers could be required to compute the VDF output for a given block and submit the result along with the block. Transactions could then be ordered prior to the block that reveals the VDF result, and mined after that block.

Caveats around VDF difficulty tuning being hard.

Note: This works much better in a PoS world where block producers know when their turn is in advance, and they can start calculating the VDF result for their block some amount of time prior to it being their turn. We can naively use the RANDAO of n blocks back as a seed for this (caveats around RANDAO being known to some actors prior to it being publicly available, so VDF difficulty tuning becomes even harder).

3 Likes
3

Thanks for your feedback :slight_smile:

We have analysed a scheme similar to what youā€™ve mentioned above and weā€™re planning to dive deeper into this along in our roadmap.

Hereā€™s the research paper we analysed: https://eprint.iacr.org/2021/1293.pdf

3 Likes
4

This is quite an achievment!

Iā€™d like to point out that this schema supports distributed computation of time-lock puzzles, and optimistically it should even be reasonable for everyone to give the sequencer ā€œadviceā€ on the solution of their time-lock puzzle after the order of txs is finalized.

I wonder how could you motivate this behavior by cryptoeconomics? Do you have any ideas?

EDIT: On the second read, do I understand correctly that trader provides the signature AFTER they see the order of txs? Why so? I think there is a censorship attack potential at this stage, sequencer decrypts transactions and then just drops the ones it doesnā€™t like, pretending no signature is sent??

Iā€™d like to point out that transaction encryption gives a wonderful possiblity of censorship resistance due to sequencer not knowing what to censor! This is an extremely powerful proposition, it would be really sad if it goes to waste.

EDIT2: Also, do I understand correctly that irrespective of a chosen method of proof generation of time-lock puzzle this proof can be precomputed? So actually for a trader it wouldnā€™t be 540 seconds, but would be almost instant, with precomputation offline phase taking 540 seconds?

2 Likes
5

This is a cool idea but it can only remove frontrunning MEV and other solutions are needed for other kind of MEV. I wonder how the scheme deals with gas and validator fees? As the validator does not know how heavy a certain transaction is beforehand as its under a complete ZK. The transaction can be too big to fit into a block. This can be avoided by not making the validator payment ZK and also the size of the transaction could also be public information. This still leaves the computation cost that needs to be revealed beforehand, which is impossible to do as it can depend on the order.

I guess this means we can only enable a very limited set of transactions and not just any EVM transactions are ok?

2 Likes
6

I think you can publish gas limit and gas price in the open?

And enforce sorting by gas price, that removes all MEV but blind removal of unknown transactions (~ removal of everything but your transactions to arb alone and in peace).

1 Like
7

Blocks are filled by gas used, not gas limit. If you fill by gas limit, someone can create a transaction that costs 30,000 gas but has a gas limit of 30,000,000 and the block will be ā€œfullā€ even though the transaction didnā€™t actually do anything.

1 Like
8

Yeah, we will need to always burn the remaining gas, thats the difference with current EVM behavior where it is refunded.

1 Like
9

This would mean that the throughput of the chain is unnecessarily low. One could imagine a mechanism for making up for the unused blockspace, but it would add notable complexity.

1 Like
10

I donā€™t think it will make it unnecesarily low - it is economically feasible to provide honest estimate on gas, then.

1 Like
11

The problem is that many transactions have gas usage that changes greatly depending on order. For example, a Uniswap transaction that fails will use significantly less gas than a Uniswap transaction that succeeds. This change would make all code paths cost the worst case amount of gas, even if they use significantly less.

1 Like
12

Thank you for your good question!

The tradersā€™ ā€œadviceā€ may be an option, but we havenā€™t thought about it enough yet. We believe that communication between traders and operators should not be inevitable for protocols to be guaranteed. The operator should be able to get its decision key without additional external data. This is also why we thought time-lock puzzle-based encryption was a better solution than a threshold.
If the option makes a better protocol, I think we should consider that. For this, there may be crypto-economics such as commission discounts, but it is not yet considered.

Sending a signature to the operator is one way to ensure that a committed order is carried out. The operator receives the signature and creates proof with it, the verifier contract can verify the integrity of the order.
The operator must execute the transactions in the order committed to the MMR, regardless of receiving the traderā€™s signature. Therefore, it can be said that the operator did not receive the signature, but the transaction cannot be dropped based on this. However, if the operator performs differently than the committed order, the trader must challenge to verifier contract on L1. In this case, the confirmation may be delayed due to a challenge period.

The proof is used to prove not only the time-lock puzzle but also the encryption and validity of transaction. So the proof canā€™t be made without knowing whatā€™s in a transaction to be encrypted and verified. so it can be done in advance. The transaction should be synced with the current state of the network.

1 Like
13

Our first target was a type of sandwich attack that leads to userā€™s financial loss. As you mentioned, other MEVs like back-running havenā€™t not been discussed enough. Random ordering might be one of candidates to prevent them. will keep researching on that. Thanks for pointing that out. please let me know other types of MEVs we should condier.

Zk rollups can only execute a specific type of transactions. So there will be no too heavy transactions for the system since the types of tx are predetermined and intergated into zk circuits. However if we expand to zkEVM for our system, your concern would be resolved. Through they active discussion, we have also begun to discuss some ideas.

  1. The operator does not encrypt information (gas fee, gas price) that can determine the amount of computation.
  2. Information that can identify computation of heavy transaction in advance is stored in the validity proof.
    We will leave this as an open discussion and actively discuss it together.

I would like to thank @levs57 and @MicahZoltu for their participation in the discussion.

2 Likes
14

Thanks for your answer! Considering censorship attack, I donā€™t really understand, why do we even collect signatures in the phase 3. What happens if some signatures did not arrive?

On precomputation - you can precompute it! You split proof into two pieces ā€œhere is time lock puzzle, and its answer x has Hash(x)=yā€, y being some public value. And second piece ā€œhere is correct transaction, encrypted with key x, such that Hash(x)=yā€, y being some public value.

Then, the first part (timelock puzzle) can be precomputed!

2 Likes
15

I understand your question!

Our goal is to find a way to finalize the state without a challenge period, and collecting the signatures was one of the methods we came up with. So yes, unfortunately, there can be a censorship attack. But if you know a better way to get rid of the challenge period, I hope you can talk with us.

Yes, I tried the method you mentioned at first! I divided the zkp circuit into two and calculated the time-lock puzzle and encryption separately. I do think that precomputing the time-lock puzzle is a good idea.

However, this method requires a commitment that connects two circuits. Also, it needed storage of parameters (e.g. CRS) and a lot of computation operations (540 seconds).

So this is why we developed PVDE, a method that calculates time-lock puzzles and encryption in one circuit, but requires smaller computing power (just 5 seconds!). If I had not develop PVDE, I would have used the precomputation method. Iā€™ll share all our studies on Ethereum Research later!

1 Like
16

Thanks so much for your effect, but I am just wondering is there any other way for the trader to generate false validity proof and perform a DoS attack? And in Phase 3, what happens when the trader checks that the time to receive the commitment from the operator is longer than the minimum time-lock puzzle computation time? Is the transaction simply canceled? If so, when the trader submits the transaction again, doesnā€™t the trader already know the content of the transaction and might do MEV again? Sorry if those questions are trivial. Thanks in advance.

1 Like
17

This is a really interesting and quite novel approach. One question I have though: do you have any estimates around the extra computational load placed on the operator from having to solve and decrypt time-lock puzzles? Creating a proof for a zk-rollup is already very computationally expensive, what impact would this scheme have?

Also, does this scheme allow for only a subset of transactions in each block to be time-locked, is there a way that non-MEV-sensitive transactions can just not use the scheme?

Have you thought what possible incentives there might be for transaction senders to not sign and return the transaction order commitments? What happens in the case that they decide to withhold, does the transaction still get processed?

(apologies for the barage of questions - itā€™s a genuinely interesting scheme)

2 Likes
18

Hi, @vicshi06

Thank you for your question. Your question is by no means trivial and it is one of the things we have been pondering so far.

Since we generate a validity proof with zkp, The possibility that the verification result of the false validity proof is true is negligible. Therefore, there is no possibility of being DoS attacks by false validity proof. If you have other ideas, weā€™d like to talk about it with you :slight_smile:

If the operator sends a commitment to the trader later than the minimum computation time, currently, we think the trader should not accept it. We are considering a way to declare that traders have not accepted, one of which is they do not sign a commitment.

The traders will challenge, noting that they did not submit their signature. Of course, the operator can execute the order according to its own commitment without the tradersā€™ signature, because the trader can accidentally or maliciously fail to submit the sig.

We know that this method is contrary to the purpose of finalizing without the challenge (in open for discussion). So, weā€™re still considering another way.

The symmetric key is one-time key. In other word, each key should be used once and the transaction is encrypted, so the operator cannot attempt MEV with the transaction sent again by the trader.

1 Like
19

Hi, @simbro

Thank you for your interesting!

Since the time-lock puzzle requires sequential computing, the operator may have to use multiple cores if there are many transactions to be processed. To optimization, we are looking at new schemes such as one encryption key for all traders in one round. The validity of a membership proof for the MMR tree is added to the circuit of zk rollups. In the circuit, the condition is to check whether the transaction belongs to the MMR tree.

The non-MEV-sensitive transactions will also be supported, and we are designing them. If you have a good way, I hope we can talk together.

We are seriously considering this, and i think the answer I left to @vicshi06 will be the answer to your question :slightly_smiling_face:

2 Likes