Octopus Contract and its Applications

[SoraSuegami]

Authors: Sora Suegami, Leona Hioki

Thank Yi Sun, Justin Drake, and Aayush Gupta for feedback and discussions.

Our full paper is here: Octopus Contract and its Applications

TL;DR

We propose the concept of Octopus contracts, smart contracts that operate ciphertexts outside the blockchain. Octopus contracts can control the decryption of the ciphertexts based on on-chain conditions by requesting validators to sign the specified messages. Signature-based witness encryption (SWE) enables users to decrypt them with the signatures. Moreover, Octopus contracts can evaluate arbitrary functions on encrypted inputs with one-time programs built from SWE and garbled circuits. These features extend the functionality of smart contracts beyond the blockchain, providing practical solutions for unresolved problems such as a trustless bridge for a two-way peg between Bitcoin and Ethereum, private AMM, minimal anti-collusion infrastructure without a centralized operator, and achieving new applications such as private and unique human ID with proof of attribution, private computation with web data, and more.

1 Background and Our Contribution

Regarding the aspect of using smart contracts to operate secrets outside the blockchain, our scheme is fundamentally a generalization of the author’s previous work Trustless Bitcoin Bridge with Witness Encryption (Leona Hioki), which also provides a practical construction of the previous work.

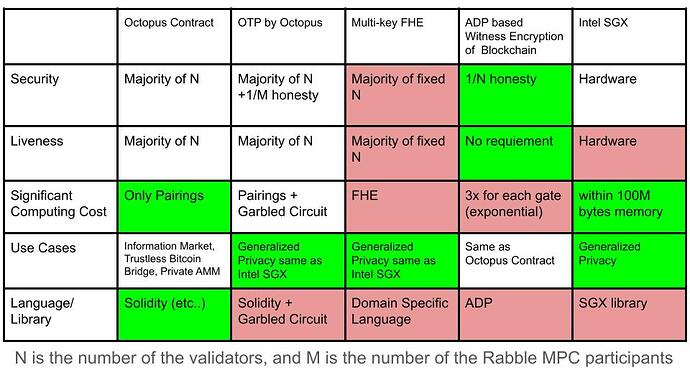
Compared to existing schemes to allow smart contracts to operate ciphertexts using new cryptographic schemes, e.g., Lit protocol with threshold encryption, smart contracts with secret sharing multi-party computation (MPC), and smartFHE with fully homomorphic encryption (FHE), our scheme with SWE requires minimum modification to the node implementation of the validators. This is because the validators only need to sign the message specified by the Octopus contract and encrypt this signature with public-key encryption (PKE). Especially, when a circuit of the function is privately evaluated with one-time programs (OTPs), the validators’ computational cost only depends on the input size of the circuit, independent of the circuit size. Besides, while both FHE-based schemes and our scheme can delegate heavy evaluation of the circuit to an untrusted third party, the latter is estimated to be faster than the former because the delegated party in the latter just decrypts the SWE encryptions of the garbled inputs and evaluates a garbled circuit, which only employs a hash function and bit operations in the optimal construction.

The validators’ work in vetKeys is similar to ours: the validators generate BLS signatures for an ID and encrypt the signatures under the user’s public key to pass the user a private key of that ID in ID-based encryption. However, it is our novel point to use the signatures for the private evaluation of functions on encrypted inputs.

Despite the above advantages of our scheme, the Octopus contract using OTPs further relies on rabble MPC, n-of-n MPC among randomly selected people who are different from the validators. It is used to generate an OTP while embedding a private key unknown to humans in the evaluated circuit. The rabble MPC is more secure and feasible than existing MPC-based schemes for the following reasons:

1. If at least one participant is honest, the MPC is secure, i.e., revealing no information other than the OTP.
2. Even if the MPC fails because some participants leave the MPC, different participants can start new MPCs any number of times. Also, many MPCs can be performed in parallel.
3. Once the OTP is generated, there is nothing more for the MPC participant to do.

The following table summarizes the comparison between our scheme and the existing schemes.

2 Signature-based Witness Encryption

2.1 Definition of SWE

We adopt a SWE scheme defined for t-out-of-n BLS signatures. It provides the following algorithms. While they are based on Definition 1 of McFly, some inputs are omitted or modified.

1. \textsf{ct} \leftarrow \textsf{SWE.Enc}(V=(\textsf{vk}_1, \dots, \textsf{vk}_n), h, m): it takes as input a set V of n BLS verification keys, a hash h of a signing target T, and a message to be encrypted m. It outputs a ciphertext \textsf{ct}.
2. m \leftarrow \textsf{SWE.Dec}(\textsf{ct}, \sigma, U, V): it takes as input a ciphertext \textsf{ct}, an aggregate signature \sigma, two sets U, V of BLS verification keys. It outputs a decrypted message m or the symbol \perp.

If more than or equal to t validators of which verification keys are in V, i.e., |U| \geq t and U \subseteq V, generate a valid aggregated signature \sigma for the hash h, the correctness holds, i.e., \textsf{SWE.Dec}(\textsf{SWE.Enc}(V=(\textsf{vk}_1, \dots, \textsf{vk}_n), h, m), \sigma, U, V) = m. Otherwise, the \textsf{SWE.Dec} algorithm returns the symbol \perp. Therefore, once the validators release the signature \sigma, anyone can decrypt the ciphertext \textsf{ct}.

2.2 Access-Control of the Signature

We use the same technique as vetKeys to control who will be able to decrypt the ciphertext by encrypting the validators’ signatures. Specifically, when a legitimate decryptor provides a public key \textsf{pubKey} of the PKE scheme, each validator publishes an encryption \textsf{ct}_{\sigma_i} of the signature \sigma_i under \textsf{pubKey}, i.e., \textsf{ct}_{\sigma_i} \leftarrow \textsf{PKE.Enc}(\textsf{pubKey}, \sigma_i). That decryptor can recover the message by decrypting each \textsf{ct}_{\sigma_i} with the private key \textsf{privKey} corresponding to the \textsf{pubKey}, aggregating the recovered signatures into \sigma_{\Sigma}, and decrypting the ciphertext under SWE by \sigma_{\Sigma}. However, the other users cannot do that because they cannot obtain \sigma_{\Sigma} from \textsf{ct}_{\sigma} without \textsf{privKey}. Besides, even the validators cannot decrypt them as long as their honest majority does not reveal each signature \sigma_i.

As proposed in vetKeys, if the PKE scheme is additive-homomorphic, e.g., EC-ElGamal encryption, the decryptor can first compute the encryption of the aggregated signature by computing the weighted sum of the encrypted signatures and then decrypt only the aggregated one. By outsourcing that computation, the decryptor can reduce the computation cost.

2.3 Estimated Benchmark of SWE

We estimate a benchmark of the SWE scheme based on McFly assuming a threshold \frac{t}{n}=\frac{2}{3}. For n=500 and n=2000, encryption takes approximately 10 and 60 seconds, and decryption takes around 20 and 350 seconds, respectively. These results suggest the appropriate number of allocated validators for each use case. They also imply that more improvement in the SWE scheme will enhance the security of ciphertexts, i.e., increasing the number of allocated validators, without sacrificing the performance.

3 Octopus Contract

In our scheme, the Octopus contract helps users request the Ethereum validators to sign a specific message for the SWE decryption. Specifically, they work as follows.

1. Firstly, some validators register with and watch the Octopus contract made by an application developer.
2. An encryptor, the user willing to encrypt a message using SWE, calls the Octopus contract to register a signing target T.
3. The Octopus contract records the hash h:=\textsf{Hash}(\textsf{PREFIX}, T) derived from T. Note that \textsf{PREFIX} is a fixed unique string, which prevents the validators from signing messages for the Ethereum consensus algorithm.
4. The encryptor generates an encryption \textsf{ct} of the messages m under the hash h and n validators’ verification keys V=(\textsf{vk}_1, \dots, \textsf{vk}_n) allocated by the Octopus contract.
5. A decryptor, a user willing to decrypt \textsf{ct}, has a PKE key pair (\textsf{privKey}, \textsf{pubKey}) and calls the Octopus contract, passing the h and the PKE public key \textsf{pubKey} to request validators’ signatures.
6. The Octopus contract checks if the decryptor is legitimate based on the required on-chain conditions. If the decryptor does not pass the conditions, the contract rejects the decryptor’s request.
7. More than or equal to t validators generate the encryption ct_{\sigma} of the aggregated signature \sigma for the hash h in a way described in Subsection 2.2.
8. The validators provide the Octopus contract with the encryptions \textsf{ct}_{\sigma} along with a proof \pi to prove that they are valid encryptions of the aggregated signatures.
9. The decryptor first decrypts \textsf{ct}_{\sigma} with \textsf{privKey} to obtain the signature \sigma, and then decrypts \textsf{ct} with \sigma to recover the messages m.

In this way, the encryptor can encrypt messages under some on-chain state conditions without knowing who satisfies the conditions in the future. As long as more than or equal to the threshold of the validators behave honestly, i.e., sign only the message confirmed by the Octopus contract, only the legitimate decryptor can decrypt the ciphertext.

When implementing our scheme, we can prepare a shared smart contract for common management of the registered validators and requests for signatures. Each application contract specifies the signing messages and checks if the decryptor is legitimate.

Its application is described in Subsection 3.1 in the full paper.

4 One-Time Program with Octopus Contract

4.1 Basic Ideas

The Octopus contract with SWE described above has the following limitations.

1. The ciphertext must be decrypted in a rather short time because the validators that can generate signatures for the decryption are fixed at the time of encryption.
2. It is impossible to apply some functions to the encrypted message m without revealing it to the decryptor.

We solve them by introducing OTPs. The OTP is an encoded circuit that can be evaluated on at most one input. Goyal constructs a blockchain-based one-time program (BOTP) from witness encryption (WE) and garbled circuits. A generator of BOTP makes a garbled circuit of the circuit and encrypts its garbled inputs under WE. Its evaluator can decrypt each encryption of the garbled input for the bit b \in \{0,1\} of the i-th input bit by committing b as the i-th input bit on-chain. Subsequently, the decryptor evaluates the garbled circuit with the recovered garbled inputs. The decryptor can input only one bit b for each input bit to the circuit because the decryption condition of WE requires the decryptor to prove that b is committed first to the blockchain finalized by the honest majority of validators. In other words, the decryptor cannot input 1-b without tampering with the finalized block containing the commitment of b.

While the OTP has the limitation of one-time input, it has a useful security feature that the evaluator cannot learn non-trivial information about the circuit. Therefore, the generator can embed secret data and algorithms in the circuit of the OTP. Moreover, if multiple generators use n-of-n MPC, which we call rabble MPC, to generate a private key, embed it in the circuit, and output its OTP, the OTP can hold a private key that no human knows as long as at least one MPC participant and the honest majority of the validators are honest. It can be used to decrypt the encryption of the circuit input and sign the circuit output inside the circuit. For example, the OTP with the embedded private key allows us to bootstrap a SWE ciphertext, i.e., encrypting the same message under a different set of verifying keys. The OTP for the SWE bootstrap decrypts the encrypted signature with the private key, uses the signature to recover the message from the SWE ciphertext, and encrypts the same message under new verifying keys. We can generalize this approach to evaluate arbitrary functions on encrypted inputs.

4.2 One-time program based on SWE

Instead of existing WE constructions supporting general decryption conditions, which are impractical or depend on heuristics cryptographic assumptions, we adopt SWE to build OTPs. Let k_{i,b} and \widetilde{C} be a garbled input for the bit b of the i-th input bit and a garbled circuit of the input size |x|, respectively. The generator, the evaluator, and the Octopus contract managing \widetilde{C} collaborate as below:

1. The generator registers 2|x| signing targets \{(i,b)\}_{i \in [|x|], b \in \{0,1\}} = \{(1,0), (1,1), \dots, (|x|,0), (|x|,1)\} with the Octopus contract.
2. The Octopus contract records 2|x| hashes \{h_{i,b}=\textsf{Hash}(\textsf{PREFIX}, (i,b))\}_{i \in [|x|], b \in \{0,1\}} and allocates n validators of which the verification keys are V=(\textsf{vk}_1, \dots, \textsf{vk}_n).
3. The generator generates a garbled circuit \widetilde{C} and its garbled inputs \{k_{i,b}\}_{i \in [|x|], b \in \{0,1\}}.
4. For each i \in [|x|], b \in \{0,1\}, the generator encrypts k_{i,b} under V and h_{i,b}, i.e., ct_{i,b} \leftarrow \textsf{SWE.Enc}(V, h_{i,b}, k_{i,b}).
5. The evaluator registers the input x with the Octopus contract.
6. The Octopus contract checks if the other inputs have not been registered before. If so, it requests the allocated validators to sign the |x| hashes \{h_{i,x_i}\}_{i \in [|x|]} without specifying a public key to encrypt the signatures.
7. The evaluator obtains aggregated signatures \{\sigma_{i}\}_{i \in [|x|]} and uses them to decrypt \{ct_{i,x_i}\}_{i \in [|x|]}, i.e., k_{i,x_i} \leftarrow \textsf{SWE.Dec}(ct_{i,x_i}, \sigma_{i}, U, V).
8. The evaluator evaluates \widetilde{C} on \{k_{i,x_i}\}_{i \in [|x|]}.

Notably, in formal security proof, the garbled circuit is secure only against a selective adversary that chooses the input x before seeing the garbled circuit \widetilde{C}. However, as far as our knowledge, it does not mean that there is a practical attack on the garbled circuit scheme when x is chosen adaptively. Besides, Yao’s garbled circuit without modification is proven to be adaptively secure if the circuit is an NC1 circuit, i.e., a low-depth circuit. To bootstrap it to a polynomial-sized circuit, we may be able to use a similar technique in this paper that bootstraps an indistinguishability obfuscation of NC1 circuits with a randomized encoding such as Yao’s garbled circuit.

4.3 Rabble MPC for Key-Embedded OTPs

OTPs of key-embedded circuits are generated through the rabble MPC, n-of-n MPC among randomly selected people. The Octopus contract manages the participants of the rabble MPC and randomly assigns their subset to each generation of the OTP. These participants are different from the validators, and the Octopus contract can require a lower stake to participate in the rabble MPC than that of validators.

After registering the signing targets with the Octopus contract as described above, the selected n participants perform the n-of-n MPC to privately generate a new OTP for a circuit C taking s inputs as follows:

1. Each participant provides the randomness r_i as input.
2. They derive private and public keys (\textsf{privKey}, \textsf{pubKey}) from the XOR of all randomnesses \bigoplus_{i=1}^n r_i. These keys are assumed to be usable for both PKE and digital signature schemes.
3. They construct a key-embedded circuit C[\textsf{privKey}] that takes s encryptions of inputs (ct_{x_1}, \dots, ct_{x_s}) under \textsf{pubKey}, decrypts them with \textsf{privKey}, provides the s inputs (x_1, \dots, x_s) for C, signs the output y=C(x_1, \dots, x_s) with \textsf{privKey}, and outputs y and the signature \sigma_{\textsf{otp}}. Let u be the input bits size of C[\textsf{privKey}].
4. They generate a garbled circuit of C[\textsf{privKey}] denoted by \widetilde{C[\textsf{privKey}]} and its garbled inputs \{k_{i,b}\}_{i \in [u], b \in \{0,1\}}.
5. They encrypt each garbled input k_{i,b} under the allocated validators’ verification keys V and the hash h_{i,b}=\textsf{Hash}(\textsf{PREFIX}, (i,b)), i.e., ct_{i,b} \leftarrow \textsf{SWE.Enc}(V, h_{i,b}, k_{i,b}).
6. They outputs the OTP (\textsf{pubKey}, \widetilde{C[\textsf{privKey}]}, \{ct_{i,b}\}_{i \in [u], b \in \{0,1\}}).

The way of the SWE bootstrapping and the applications with OTP are described in Subsections 4.4 and 4.5 in the full paper.

5 Selecting a Subset of Validators

There are several methods to select a validator set from the consensus layer of Ethereum as follows:

1. Hard fork Ethereum to force all validators to sign messages from Octopus contracts.
2. Soft fork Ethereum, allowing any validators to sign messages from Octopus contracts.
3. Use a re-staking mechanism such as Eigen Layer, enabling validators to have dual roles.

Even in the first case, which imposes the greatest burden on the Ethereum network, the validators’ signatures for the same messages can be aggregated, so that the additional cost of pairing is at most for each ciphertext. However, in that case, we should note that security is not completely inherited because the validators cannot be penalized in the same way as in the case of double voting when they sign messages not specified by the Octopus contracts.

In the second and third cases, we can maintain the existing protocol of the consensus layer as the modification to the node implementation for our scheme is optimal in similar to MEV-related protocols. While the restaking in the third case is easy to introduce, the soft fork supported by many validators will improve the security of our scheme more significantly.

Applications and the other notes

The on-chain conditions for the decryption in Octopus contracts can be implemented in Solidity. By customizing the conditions for each use case, we can build various novel applications, including a trustless bitcoin bridge, private AMM, and more. The OTP extends the application of the Octopus contracts because their functionalities are almost equivalent to what TEEs can do, in particular verification of computations by private conditions, private unique human IDs with proof of attributions, and private computation with web data. They are described in our full paper.

Read our full paper here: Octopus Contract and its Applications

Sora Suegami wrote the sections about the idea of using OTPs for private function evaluation and its applications. Leona Hioki wrote the sections about a trustless bitcoin bridge and private AMM. The other sections are written together.

[sg]

Okay so my takeaways and rephrasal for further discussion below.

• The Octopus Contract receives and stores ciphertext as input.

• The logic described in the smart contract determines the entity that can decrypt the ciphertext.

• The information required for decryption is a threshold signature by the validators that comprise the consensus layer. This mechanism is called SWE and is based on the honest majority assumption. Those signers are fixed at encryption timing without One-time Programs (OTPs).

• The method for securely returning signatures to a qualifying sender is on-chain public key cryptography.

• Unlike the method using FHE, the validator only needs to pay the computational cost of the threshold signature, and the computational cost of the decryption process is paid by the sender, which is novel.

• With OTPs, ciphertext (such as encrypted private key) could be used for generating a signature to run a new tx without revealing that key. (It can be a shared account of different blockchain, etc.)

• In chapter 5, several L1 modification ideas.

---

I would like to ask a question.

• In chapter 4 section 2 “One-time Program with SWE”, the evaluator seems to be trusted. Could you tell me his plausible assumption for security?

[SoraSuegami]

Thank you for your questions!

The Octopus Contract receives and stores ciphertext as input.

Yes.
However, the encryptor does not necessarily store the ciphertext on-chain in applications that ensure the availability of the ciphertext in any other way.

The logic described in the smart contract determines the entity that can decrypt the ciphertext.

Yes. Its interesting point is that the encryptor does not need to specify the decryptor in advance.

The information required for decryption is a threshold signature by the validators that comprise the consensus layer. This mechanism is called SWE and is based on the honest majority assumption. Those signers are fixed at encryption timing without One-time Programs (OTPs).

Yes.

The method for securely returning signatures to a qualifying sender is on-chain public key cryptography.

Yes, the decryptor just specifies a public key, and the validators return encryptions of the signature under the public key.

Unlike the method using FHE, the validator only needs to pay the computational cost of the threshold signature, and the computational cost of the decryption process is paid by the sender, which is novel.

The validators in our scheme only need to generate the threshold signature to help the evaluation of OTPs.
However, the validators in multi-key FHE can also delegate a heavy evaluation of which computational cost depends on the circuit size to an untrusted party, i.e., the evaluator.
We can estimate that the computational cost in our scheme is cheaper than that in the FHE-based schemes.
The detail is described in Section 1 of our full paper.

With OTPs, ciphertext (such as encrypted private key) could be used for generating a signature to run a new tx without revealing that key. (It can be a shared account of different blockchain, etc.)

We assume the key-embedded circuit always outputs a signature for the circuit output. The encryptions of garbled inputs under SWE are used to evaluate the garbled circuit, which outputs the circuit output and its signature, without revealing the embedded private key.

In chapter 5, several L1 modification ideas.

Yes, we present multiple ways to modify the node implementation of the validators for our scheme.

In chapter 4 section 2 “One-time Program with SWE”, the evaluator seems to be trusted. Could you tell me his plausible assumption for security?

There is no assumption about the evaluator because the evaluator cannot learn any information in the circuit, e.g., the embedded private key.
What makes you think that the evaluator is trusted?

[sg]

Thanks to your feedback, I learned what the garbled circuit and the evaluator are. Seems legit

[tkmct]

PREFIX of a hash is open to the public? Then, an evaluator’s input to the OTP has to be made public?

[SoraSuegami]

Thank you for your questions!

PREFIX of a hash is open to the public?

Yes.

Then, an evaluator’s input to the OTP has to be made public?

No, they are encrypted under a public key of the private key embedded in the circuit of the OTP.
The description in Subsection 4.2 handles OTPs for general circuits and the inputs are directly recorded on-chain.
However, our actual construction in Subsection 4.3 only assumes OTPs for the key-embedded circuits, which decrypt the encrypted inputs with the embedded private keys.
Therefore, even if the circuit inputs to the key-embedded circuits, i.e., the encrypted inputs, are public, the actual inputs are kept private.

[tkmct]

Thank you for your answer!
So, does the evaluator commit to encrypted inputs on-chain? How does this process work in detail?
I assume that even though the evaluator’s input (represented as a series of bits) is encrypted under pubKey of embedded GC, each input bit can be easily guessed because possible ciphertexts are either encryption of 0 or 1. This is why I asked if PREFIX is public, so that anyone can calculate the hash of evaluator’s inputs.

[maniou-T]

What is the role of the rabble MPC (n-of-n MPC among randomly selected participants) in the generation of One-Time Programs (OTPs) with key-embedded circuits, and how does it contribute to the security of the proposed scheme?

[SoraSuegami]

So, does the evaluator commit to encrypted inputs on-chain? How does this process work in detail?

Yes. Specifically, the evaluator encrypts the input x under a public key \textsf{pubKey} of the private key embedded in the circuit and commits each bit ct_x[i] of the ciphertext ct_x.
If no encrypt input has been committed on-chain, the contract requests validators to sign a signing target (i, ct_x[i]) for each i.
The validators’ signature for (i, ct_x[i]) will allow the evaluator to decrypt the SWE encryption of the i-th garbled input for the bit ct_x[i], which is generated at the generation of OTP.

each input bit can be easily guessed because possible ciphertexts are either encryption of 0 or 1.

This is not true.
For example, if the circuit only takes input from one party, the ciphertext will be the encryption of the entire input bits.
Even if the encrypted input is just an encryption of one bit, I think the adversary cannot predict which bit is encrypted as long as the PKE scheme is IND-CPA secure.

[SoraSuegami]

Thank you for your question!

What is the role of the rabble MPC

In short, the role of rabble MPC is a trusted generation of the OTP of the key-embedded circuit.
Specifically, it first generates a private key unknown to any participants, then embeds the key into a circuit, and finally outputs only the OTP, i.e., a garbled circuit, SWE encryptions of garbled inputs, and a public key of the embedded private key.

how does it contribute to the security of the proposed scheme?

As long as at least one participant in the rabble MPC (and the honest majority of the validators) is honest, i.e., not revealing intermediate values in the MPC, the Octopus contract can assume that the embedded private key is unknown to anybody and can be used only according to the logic of the key-embedded circuit, similar to the private key in an enclave of TEE.

[leohio]

There were 2 questions for me, and seems that I need to follow them.

1. Should we make a bigger size of validator sets to make SWE secure?

Attackers in the validator set can collude to decrypt the SWE ciphertexts without the smart contract execution. But one of the colluders will be rewarded for revealing that activity to make them slashed.
If in such a condition, even trying that is dangerous for them.
But the size of validators matters of course, and the best case is all the Ethereum validators.

What kind of data is private in the section of Private AMM?

Only the transactor can see the AMM pool when they send the tokens to swap.
Deposits and withdrawals are with token transfers in a private manner operated by the other services.
In the trusted setup, an MPC process is required not to let the last person know the address to make 1/N secret assumption of privacy, otherwise, the last person can see a part of the pool (one deposit address). If you fully trust the trusted setup, the last person only has to forget the pool after making the SWE ciphertext.
As it describes, only a person who swaps tokens can see the pool temporarily and the pool gets changed after the transaction. So this AMM is somehow hard to trace activities as a semi-private AMM.

[turboblitz]

Great paper!
Still trying to wrap my head around the OTP part.

For the trustless bitcoin bridge section, I have a question. Let’s consider a simpler design without WE, a traditional multisig bridge on top of eigenlayer:

• A user deposits btc to the multisig address controlled by the nodes.
• He proves transaction on ethereum with a light client bridge, mints tBTC.
• When he wants to withdraw, burns tBTC specifying a BTC withdrawal address
• Each node signs a transaction that sends the correct amount of btc to the withdrawal address specified by the user.

If a node signs a transaction but no request has been made, it can be proven and slashed on ethereum, so 1/N trust assumption. Also, this allows for arbitrary amounts.

Does the octopus contract improve on this scheme ?

[leohio]

Even if you can slash the person, the majority of that multi-sig can steal the fund, so it’s the majority assumption, not 1/N.
In this case, the 1/N assumption is just for the trusted setup, and the majority assumption of validators. still remains. If you want the 1/N assumption, pls read here

[xiangxiecrypto]

It is a very nice idea to use SWE to construct these applications. I have a few questions.

1. Afaik the garbled circuit can not hide the information on the circuit itself, it only hides the inputs. If you want to embed secret information in the circuit, you probably need to use universal circuit?
2. In the key-embedded OTP constructions, you have to run an n-of-n MPC to securely compute all the SWE encryptions and garbling process? Do I understand correctly?
3. You mentioned that one can also use Octopus contract to delegate computation as FHE, can you explore it more? In the OTP construction, the evaluator has to compute the circuit anyway, right?

[SoraSuegami]

Sorry for the late response!

1. Afaik the garbled circuit can not hide the information on the circuit itself, it only hides the inputs. If you want to embed secret information in the circuit, you probably need to use universal circuit?

As far as I understand, some garbled circuit schemes such as Yao’s garbled circuit hide the information on the circuit. Besides, if you use a scheme that does not hide the circuit, as you mentioned, you can use a universal circuit. In that case, the OTP generation process outputs only one-bit garbled input for each bit corresponding to the circuit, rather than encrypting garbled inputs for both bits under SWE. Therefore, this approach does not increase the number of signed messages.

This paper describes the circuit privacy of garbled circuits.

041.pdf

1. In the key-embedded OTP constructions, you have to run an n-of-n MPC to securely compute all the SWE encryptions and garbling process? Do I understand correctly?

Yes, that is correct!
The point is that the garbled circuit and the SWE encryptions of the garbled inputs should be generated without revealing the used randomness to anyone.

You mentioned that one can also use Octopus contract to delegate computation as FHE, can you explore it more?

Sorry for the confusion, we just compared the delegated evaluation of private circuits in our method with that of (multi-key) FHE.

In the OTP construction, the evaluator has to compute the circuit anyway, right?

Yes, the evaluator needs to evaluate a garbled circuit.
However, we expect that this computational cost will be less than that of the FHE evaluation as described in Section 1 of our paper.

[voidp]

Interesting idea. I have two clarification questions:

Can you say more about building “anti-collusion” protocols from Octopus smart contracts? Is there some special leverage to prevent/slash collusion that is infeasible in a more general threshold trust assumption? I.e., is an Octopus smart contract more resilient to collusion than, say, an MPC with a threshold assumption?

Second, is there implementation to play with?

[wyunhao]

Hi there,
Thanks for sharing this interesting paper! I have some quick questions:

• Generally, your idea is not using the “witness” part of SWE right? What you need is just a threshold signature scheme.
• Regarding the bootstrapping, it seems that the Octopus Contract needs the original set of validators V to be online and provide the contract their aggregated signing key; also, the new set of validators should also be online to do their job, is my understanding correct?
• Following the above question, is it the case that in all applications, the original set of validators V need to be there when someone wants to evaluate/decrypt the ciphertexts “encrypted” under V? For example, in trustless bitcoin bridge case, all “signers” (which is actually the trusted-setup nodes) needs to provide the decryption of ciphertexts.

Lastly, it would be appreciated to see the evaluation of a concrete implementation. Could you please kindly share some information about your roadmap on this project?

[wooju]

Based on the SWE reference you provided, I understand that for an input message x, the SWE ciphertext consists of (2*|x|) target group elements + (2*n + 3) elements (where n is the number of keygen participants) from a group where pairing operation is defined. In this case, it seems that the length of the ciphertext would be very long… Is this also data that needs to be stored somewhere? How can the evaluator obtain this value?