Lead Author: Leona Hioki
Coauthor : 3966f482edb3843a7cdfb9ffa6840023
TL;DR: Controlling bitcoin possession by a state condition of Ethereum in a cryptographic way. A trusted setup like Groth16’s Powers of Tau ceremony is required. No need for any node with liveness.
Introduction
We propose a trustless WBTC configuration that neither depends on a custodian nor an individual that provides excessive collateral. We achieve it relying solely on a cryptographic scheme called Witness Encryption (WE). The WE scheme enables us to encrypt a secret key of Bitcoin addresses holding the deposited bitcoins, while requiring witness of WBTC amortization on the Ethereum blockchain to decrypt the ciphertext. This feature guarantees that only users who possess valid witness can recover the secret key and withdraw the deposited bitcoins.
Background
It is not easy to transfer a bitcoin to the Ethereum blockchain because the Bitcoin blockchain and the Ethereum blockchain operate independently. However, there has been a bridging mechanism to make this possible, and the cryptographic asset that utilizes this mechanism is WBTC (Wrapped Bitcoin ( WBTC ) an ERC20 token backed 1:1 with Bitcoin, n.d.).
With WBTC, when a user sends bitcoins to a third party’s bitcoin address, s/he can mint the sending amount as WBTC on the Ethereum blockchain (i.e., increases the bitcoin balance). S/he can also send WBTC to other users on the Ethereum blockchain. When a user who holds WBTC redeems WBTC on the Ethereum blockchain (i.e., decreases the bitcoin balance), the third party will send it back to the user’s Bitcoin address. In the existing schemes of WBTC, the user needs either a custodian that manages the deposited bitcoins or an individual that provides excessive collateral beyond what they need in standard financial transactions. This is because, under the programmatic form of Bitcoin Script (Script Bitcoin Wiki, n.d.) used in the Bitcoin protocol, we have thought that it is impossible to mint WBTC using cryptography alone up until now. In other words, if the Bitcoin script had the same functionality as a smart contract on the Ethereum blockchain, it would be possible to design a custodianfree WBTC by building a smart contract with logic to verify the state of the Ethereum blockchain and send the deposited bitcoins according to that state. However, the current Bitcoin script can only support few cryptographic schemes such as verifying digital signatures, so no one has believed this is possible to achieve.
Approach
We created a method that relies solely on cryptography using Witness Encryption (WE), one of the cryptographic schemes already introduced by the pioneers (Garg, Gentry, Sahai, & Waters, 2013), to realize WBTC without the need for an administrator such as a custodian or an individual with incentives. While in ordinary public-key cryptography schemes, a holder of a particular secret key can decrypt a ciphertext, in the WE scheme, s/he encrypts a message for an instance to a condition described as an NP relation, which is satisfied by inputs and witness in NP problems, and only the holder of that witness can decrypt the ciphertext (Garg et al., 2013) (Goldwasser, Kalai, Popa, Vaikuntanathan, & Zeldovich, 2013). In our proposed WBTC, the secret key is encrypted using the WE scheme, and only the user who holds the valid witness to amortize the WBTC on the Ethereum blockchain can decrypt the ciphertext when s/he provide it.
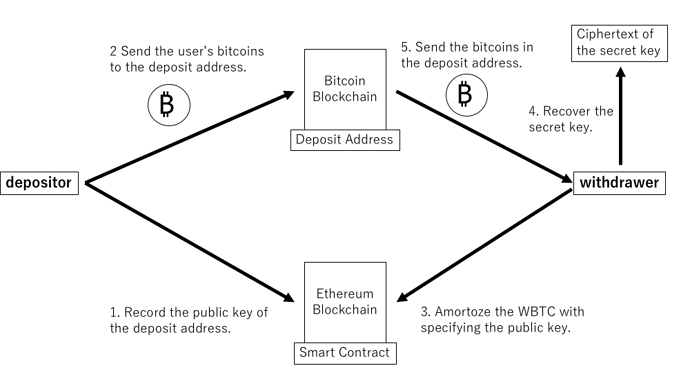
In the deposit process, a user records a public key of the Bitcoin deposit address (Bitcoin address to which a bitcoin holder sends his or her bitcoins in order to mint WBTC) in the smart contract for our program; then sends the user’s bitcoin to the address. The user generates proof of the deposit with a non-interactive zero-knowledge (NIZK) proof system. If and only if the proof passed the verification, the smart contract will mint the WBTC.
In the withdrawal process, a user first amortizes the WBTC with specifying the public key of the deposit address to be used. If the amortization process completes, the smart contracts issue an event log. Providing the above data along with the user’s digital signature, the user can recover the secret key of the deposit address from the ciphertext. The user finally sends the bitcoin in the deposit address to the user’s Bitcoin address.
While the deposit address is generated as an N-of-N multi-signature address, our system eliminates the need of liveness of any third parties or custodians. Specifically, the security of deposited bitcoins can be maintained as far as at least one of the generator behaves honestly only during address generation. This is because a malicious generator of the multi-signature address needs to collude with all of the generators to steal the fund, but a user holding a valid witness can decypt all of the secret key.
In the above process, we may identify transactions for all deposits and withdrawals with other transactions on the Bitcoin blockchain, since the deposit address is fixed. Using a random public key, we can randomize the deposited address and improve its anonymity. A user in the deposit process additionally generates a random secret/public keys and records the public key in the smart contract. The user then sends the bitcoin to a stealth address derived from the random secret key. A user in the withdrawal process recovers the secret key of the stealth address from the decrypted secret key and the random public key, so that the user can withdraw the bitcoin in the stealth address. A third party that knows neither the random secret key nor the decrypted secret key cannot derive the stealth address under the decisional Diffie–Hellman (DDH) assumption.
Detail
Detail-1: Witness Encryption
A WE scheme is defined for an NP language L (with corresponding witness relation R), and consists of the encyption and decryption algorithms (Garg et al., 2013):
WE.Enc(1λ,x,m): It takes a security parameter λ, an instance x, and a message m ∈ {0,1}. It returns a ciphertext ct.
WE.Dec(ct,w): It takes a ciphertext ct and a witness w. It returns a message m iff R(x,w) holds.
To decrypt a ciphertext ct, a valid witness w for the instance x is necessary. Therefore, no one can decrypt the ciphertext encrypted for the x \not\in \mathbb{L} (i.e. there is no witness w such that R(x,w) holds). This property is defined as ”soundness security” in (Garg et al., 2013).
(Goldwasser et al., 2013) introduced a more robust definition of security: ”extractable security”. Informally, this definition guarantees that an adversary must obtain a valid witness w from x, when the adversary can recover the message from the ciphertext for an instance x ∈ \mathbb{L}. The WE scheme used in our program should satisfy it since we encrypt any secret keys for the instances x ∈ \mathbb{L}.
In the following description of our protocol, we assume that the WE scheme is defined for the subset sum language L, which is one of the NP-complete problems. Since the circuit satisfiability problem (circuit-SAT) can be reduced to the subset sum problem, a boolean circuit C can represent the decryption condition (Bartusek et al., 2020). A message is encrypted for an instance xC depending on the circuit C. The ciphertext is decrypted if the witness w satisfies C(w) = 1.
In Appendix, we introduce a candidate of the WE scheme that we plan to adopt as the underlying WE scheme for the first implementation of our program.
To the best of our knowledge, the most practical WE scheme is ADP-based WE proposed in (Bartusek et al., 2020). While there is no security reduction to the standard assumptions for this scheme, it only uses the linear algebra, e.g. random matrix sampling, matrix multiplication, and a determinant. We review its construction in accordance with the description of (Bartusek et al., 2020), and analyze its efficiency in Appendix.
Detail-2: Deposit Bitcoin
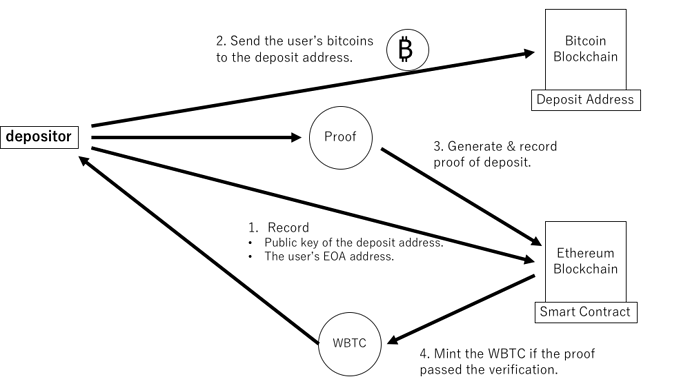
Before sending bitcoins to a deposit address, a user records the public key of the Bitcoin deposit address that s/he wishes to use in the smart contract of our program. At the same time, the user also records the user’s EOA address. Its process is necessary to prevent two users from sending bitcoins to a single Bitcoin deposit address simultaneously: s/he needs to use the Bitcoin deposit address for a single deposit and withdrawal, because its secret key has the property that the user can send all bitcoins associated with their secret key.
The fact that the user sent bitcoin to a deposit address on the Bitcoin blockchain is proved by non-interactive zero-knowledge (NIZK) proof system on the Ethereum blockchain (e.g., Groth16 (Groth, 2016), Plonk (Gabizon, Williamson, & Ciobotaru, 2019), ZK-STARK (Ben-Sasson, Bentov, Horesh, & Riabzev, 2018)). After sending bitcoins to the deposit address, the user generates a proof of deposit and records it in a smart contract in our program. Only if that proof can pass the verification process described in the smart contract will the WBTC be minted.
We implement functionality of a light client in the Bitcoin network as part of the circuit used by the NIZK proof system. However, the circuit cannot directly perform the verification of the longest chain that requires communication with other nodes (verifying which blockchain is the longest at the moment). Instead, our circuit verifies it based on the difficulty value: as a given blockchain, it accepts only those whose cumulative difficulty is greater than the minimum cumulative difficulty value fixed or adjusted in the smart contract.
If this system does not exist, i.e., only the number of succeeding blocks is verified, an attacker can generate false proofs that pass verification without recording the deposit transaction in the longest chain, as follows:
-
Create a branch of the longest chain (we will call this branch the ”private branch”).
-
Send the attacker’s bitcoins to the deposit address on the private branch.
-
Generate a new block containing the deposit transaction with taking a sufficiently long time.
-
Generate as many blocks as necessary to follow the above blocks. However, the difficulty adjustment algorithm in the Bitcoin protocol allows this process to be completed quickly by lowering the next difficulty, if the attacker intentionally declares a longer time than it took.
-
Feed the block header and deposit transaction in the private branch to our circuit to generate a proof of deposit.
-
Feed that proof to our program’s smart contract. This proof should be able to pass verification so that we can mint the WBTC.
Suppose, when the attacker includes a delayed timestamp in the block header to reduce the next difficulty, the cumulative difficulty value becomes smaller than the specified minimum value. Therefore, we can mitigate this attack by verifying the cumulative difficulty value.
To summarize the above discussion, bitcoin deposits can be realized securely by 1 to 6 as follows:
-
The format of each block header is correct (e.g., the nonce of each block header satisfies the PoW constraints).
-
Except for the last block header, the block hash of each block header is referenced as the previous block hash in the block header that follows it.
-
The first block header is the one that follows the finalized block header. However, the finalized block header is determined during address generation.
-
The cumulative difficulty value is greater than the given minimum cumulative difficulty value in the last block header.
-
The transaction format is correct, and its hash value is contained in the Merkle Root in the block header at the specified block height.
-
The recipient’s address in the transaction is equal to the deposit address, and the transfer amount is equivalent to the value fixed in the system.
Detail-3: Withdraw Bitcoin
Before all, special thanks to Barry Whitehat(Profile - barryWhiteHat - Ethereum Research) for his insight about preventing an attack from virtual malicious validators on Ethereum2.0.
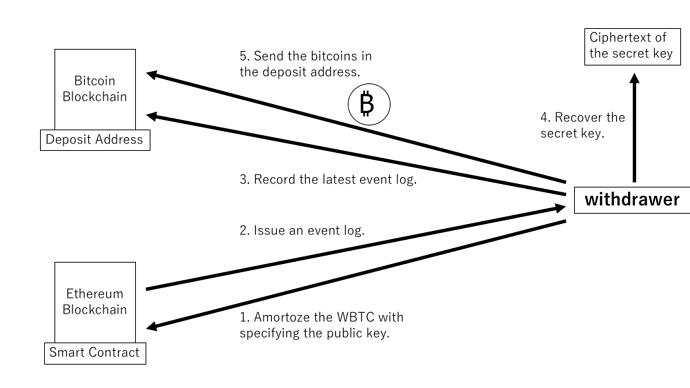
To send bitcoins from a Bitcoin deposit address, the user specifies the public key of the deposit address to be used and amortizes the same amount of WBTC on the Ethereum blockchain. To verify the result of this process, we use an event log, a record that a smart contract can publish depending on its execution. The smart contract in our program will issue an event log containing the specified public key and the user’s EOA address only if its amortization process completes without any problems.
The user then waits for the block containing the event log to be finalized in the Ethereum 2.0 blockchain. (We assume that the Ethereum 2.0 blockchain will be our program’s primary service source when it goes live.)
After finalizing that block, the user records the latest block of the Ethereum 2.0 blockchain into the Bitcoin blockchain. The Bitcoin script specification allows the ”OP_RETURN script” (Script Bitcoin Wiki, n.d.) to write arbitrary data into the transaction. Using this feature, the user records a block of data as a single bitcoin transaction. We call this transaction ”a commitment transaction”. The reason for recording the block is to prevent block cloaking attacks (so called Block Withholding Attack), in which a large group of colluding validators confirms the invalid blocks forked from the current honest chain and hides them. Those dishonest validators can escape the penalty by hiding the block, even though they are worse enough to be punished by a slashing mechanism. For this reason, our program’s system forces us to publish the same blocks used in the condition on the Bitcoin blockchain.
Finally, the user generates a digital signature using a secret key that corresponds to the user’s EOA address. The decryption condition of the WE scheme of this program requires a digital signature tied to the EOA address contained in the event log, so it guarantees that no other user can decrypt the ciphertext. Using the Bitcoin block header and Ethereum 2.0 block header (= Bitcoin/Ethereum 2.0 block header), the latest Ethereum 2.0 block, commitment transaction, event log, and the user’s digital signature as witness, the user can withdraw bitcoin securely by allowing the ciphertext to be decrypted
iff the user can satisfy the following conditions.
-
The format of each Bitcoin/Ethereum 2.0 block header is correct.
-
The block hash of each Bitcoin/Ethereum 2.0 block header is the previous block hash in the block header that follows it, except for the last one.
-
The first Bitcoin/Ethereum 2.0 block header follows the respective finalized block header. (WE encryption fixes the finalized block header.)
-
The cumulative difficulty value is greater than the minimum cumulative difficulty value in the last Bitcoin block header. (WE encryption fixes the minimum cumulative difficulty value.)
-
The latest Ethereum 2.0 block has been confirmed with a digital signature generated by a good percentage of validators.
-
The data in the block corresponding to the last Ethereum 2.0 block header is recorded in a commitment transaction, which is included in the Bitcoin block at the specified block height.
-
The event log is contained in the Ethereum 2.0 block at the specified block height.
-
The digital signature is generated by the secret key associated with the EOA address in the event log.
After recovering the secret key corresponding to the specified public key through this process, the user generates a digital signature and sends the Bitcoin to the user’s Bitcoin address.
Detail-4: Generate Bitcoin deposit address
The Bitcoin deposit address generator creates a pair of a new secret key, a public key, and a Bitcoin deposit address. These empty Bitcoin deposit addresses will not be credited with bitcoins during the pre-launch phase of our program but will be the deposit addresses after launching the service. The generator simultaneously encrypts these secret keys with WE and publishes the addresses and ciphertext.
As already mentioned, no one should expose the embedded secret key, but the generator will inevitably know the secret key. In this respect, this process requires trusting the generator. However, this trust model can be replaced to N-of-N multiple signature addresses, which can minimize the risk of a single generator.
In our model, instead of a Bitcoin deposit address generated by a single generator, an N-of-N multi-signature address associated with a public key generated by N different generators is used as the Bitcoin deposit address. Multi-Party Computation (MPC) among N parties generates the multi-signature address. Specifically, each generator generates a new secret key and a ciphertext for its WE scheme. Then, N-of-N multi-signature addresses are obtained from all of their corresponding public keys. A digital signature using all of the generated secret keys is required to send bitcoins from that multi-signature address. Therefore, no generator can send bitcoins illegally, except when all the generators collude.
However, this N-of-N multi-signature address itself is a standard method, and simply using it would require the N people in question to gather together and perform some action each time bitcoin is withdrawn, which is unrealistic in terms of operation. Therefore, while based on N-of-N multiple signature addresses, there should be no need for the generators to gather and perform some action after setup, and there should be no risk of users being unable to withdraw bitcoins. This is achievable with the following method.
The generator of each component of the N-of-N multi-signature address should first generate proof that each ciphertext was correctly constructed with the WE scheme using the NIZK proof system. If the proofs of all generators are correct, the N-of-N multiple signature address should be recorded in the smart contract. Then, due to the nature of the WE scheme, only users with legitimate witness will recover all secret keys from the ciphertext and generate digital signatures, which will allow them to withdraw the deposited bitcoins at any time.
Detail-5: Randomization for the deposit and withdrawal
Using the following technique can implement a mechanism to improve the system’s privacy in this program.
The process implementation alone in the previous sections has the drawback: we may identify transactions for all deposits and withdrawals with other transactions on the Bitcoin blockchain. However, we can let the deposit address random by adding one random public key, and the randomized address can be made indistinguishable from other addresses for any third party.
The specific procedure is as follows. (In the following description, Fp denotes a finite field of prime order p. Let G be a group of prime order p, and let G ∈ \mathbb{G} be its generator.)
The deposit process is randomized by modifying it as follows.
-
The user generates additional random secret key
r ∈ \mathbb{F}p and public key rG ∈ \mathbb{G} . -
Before sending bitcoins, the user records rG in the smart contract, along with the user’s EOA address and the specified public key of the fixed Bitcoin deposit address pkD ∈ \mathbb{G}
-
The user generates a unique stealth address (a random address that can only be obtained between two parties and cannot be distinguished from any other address by any other third party) from pkD and r. The public key corresponding to the stealth address is computed as pkD + Hash (r ·pkD )G ∈ \mathbb{G} . The user then transfers bitcoins to the stealth address.
-
Proof of deposit in the NIZK proof system provides additional proof that the recipient’s Bitcoin address is a stealth address correctly calculated from pkD and r. It also guarantees that rG is equivalent to the recorded random public key.
Similarly, the withdrawal process is randomized by modifying it as follows.
-
Obtain rG associated with the specified pkD in the WBTC amortization process.
-
Recover the secret key of the fixed public key (fixed secret key) skD ∈ \mathbb{F}p from the ciphertext, and then recover the secret key of the stealth address from skD and rG by computing skD + Hash (r · pkD ) ∈ \mathbb{F}p
-
Generate a digital signature using the secret key of the stealth address, and send bitcoin from the stealth address.
Note that we must recover skD first to recover the secret key of the stealth address (see above 2.) because pkD and r in our program generate the public key of the stealth address, while skD and a rG can obtain the secret key. This property guarantees that the user who generates the stealth address in the deposit process will not get the secret key for the stealth address.
Conclusion
In this post, we proposed the WBTC configuration using Witness Encryption. This eliminates the need for trusted custodians or individuals to cooperate in guaranteeing the value through overcollateralization. Specifically, the security of the deposited bitcoins is maintained if at least one of the participants in the MPC behaves honestly only during address generation. In addition, the anonymity of the deposited address can be improved by randomizing it with a random public key.
Appendix
Notions
Let \mathbb{N} be a positive integer, \mathbb{R} be a real number, and \mathbb{F}_p be a finite field of prime order p. For n \in \mathbb{N}, let [n] denote the set \{1,\dots,n\}. x \xleftarrow{U} X means to extract a random number x uniformly from X. Let \mathbb{G} be a group of prime order p, and let G \in \mathbb{G} be its generator.
The vector \boldsymbol{a} is \boldsymbol{a}\in \mathbb{F}_p^n in bold lowercase letters and \boldsymbol{A} is \boldsymbol{A}\in \mathbb{F}_p^{n \times n} in bold uppercase letters. The inner product of \boldsymbol{A} and \boldsymbol{B} is denoted by <\boldsymbol{A},\boldsymbol{B}>. The det(\boldsymbol{A}) denotes the determinant of matrix \boldsymbol{A}.
We use \lambda as a security parameter. The function negl(\lambda): \mathbb{N} \rightarrow \mathbb{R} exploits the property that a function negl(\lambda) is said to be negligible if for any constant c>0 there exists n \in \mathbb{N} such that negl(\lambda) < \lambda^{-c} for all \lambda > n.
ADP-based Witness Encryption
We review the ADP-based witness encryption scheme proposed in (Bartusek, “Affine determinant programs”). Note that all of the descriptions in this section are described in (Bartusek, “Affine determinant programs”).
As described in section 3 in (Bartusek, “Affine determinant programs”), an affine determinant program (ADP) is denoted by an affine function \boldsymbol{M}, which consists of (n+1)-tuple of regular matrices whose width is k:
M := (A, \boldsymbol{B_1},\dots,\mathbb{B_n}) \in \mathbb{F}_p^{k \times k} \times \dots \times \mathbb{F}_p^{k \times k}
The affine function \boldsymbol{M}: \{0,1\}^n \rightarrow F_p^{k \times k} takes an n-length binary input \mathbb{x} \in \{0,1\}^n and evaluate it by the following matrix calculation.
\boldsymbol{M}(\boldsymbol{x}) := \boldsymbol{A}+\sum_{i \in [n]} x_i\boldsymbol{B_i}.
The ADP includes an evaluation function that takes the binary input \mathbb{x}, and outputs a single bit 0/1 depending on whether det(\boldsymbol{M}(\boldsymbol{x})) is zero. In other words, its evaluation result is decided if the \boldsymbol{M}(\boldsymbol{x}) is full-rank matrix or not.
The ADP can represent an instance of the subset-sum language L, which consists of (\boldsymbol{h},\ell) \in \mathbb{F}_p^{n} \times \mathbb{F}_p. If and only if (\boldsymbol{h},\ell) \in L, there is a witness \mathbb{w} \in \{0,1\}^n such that <\boldsymbol{h},\boldsymbol{w}>=\ell. Following the definition in section 5.1 in (Bartusek, “Affine determinant programs”), the affine function \boldsymbol{M}_{\boldsymbol{h},\ell} for (\boldsymbol{h},\ell) is generated as below:
- Sample \boldsymbol{R} \xleftarrow{U} \mathbb{F}_p^{k \times k}.
- Set \boldsymbol{A}:=-\ell \boldsymbol{R}.
- For each i \in [n], set \boldsymbol{B_i}:=h_i\boldsymbol{R}.
- Output \boldsymbol{M}_{\boldsymbol{h},\ell}=(\boldsymbol{A},\boldsymbol{B}_1,\dots,\boldsymbol{B}_n).
If the witness \boldsymbol{w} satisfies <\boldsymbol{h},\boldsymbol{w}>=\ell, the determinant of \boldsymbol{M}_{\boldsymbol{h},\ell}(\boldsymbol{w}) should be zero.
det(\boldsymbol{M}_{\boldsymbol{h},\ell}(\boldsymbol{w})) = det((-\ell+\sum_{i \in [n]} w_ih_i)\boldsymbol{R}) = 0
As the random matrix \boldsymbol{R} is full-rank with high probability, the det(\boldsymbol{M}_{\boldsymbol{h},\ell}(\boldsymbol{w'})) for the invalid witness \boldsymbol{w'} is non-zero. Hence, such ADP can decide whether the provided witness is valid for the instance of the subset-sum language.
To embed a bit message b \in \{0,1\} in the ADP, the encryptor samples a random matrix \boldsymbol{S} \xleftarrow{U} \mathbb{F}_p^{k \times k}, and adds b\boldsymbol{S} to \boldsymbol{A} in the tuple of \boldsymbol{M}_{\boldsymbol{h},\ell}.
\boldsymbol{M}_{\boldsymbol{h},\ell,b} := \boldsymbol{M}_{\boldsymbol{h},\ell} + (b\boldsymbol{S},0,\dots,0)
The decryptor who holds the valid witness \boldsymbol{w} can decrypt b by deciding whether det(\boldsymbol{M}_{\boldsymbol{h},\ell,b}(\boldsymbol{w})) is zero or non-zero. (If and only if b=1, det(\boldsymbol{M}_{\boldsymbol{h},\ell,b}(\boldsymbol{w})) \neq 0 since the matrix \boldsymbol{S} is full-rank with high probability.)
The above scheme is, however, insecure because an adversary can input an non-binary input \boldsymbol{x} \in \mathbb{F}_p^n to the ADP that satisfies <\boldsymbol{h},\boldsymbol{x}>=\ell. Such input is easily calculated by solving the simultaneous linear equations.
To prevent the non-binary input, \boldsymbol{M}_{\boldsymbol{h},\ell,b} is noised by an “All-Accept ADP (Bartusek, “Affine determinant programs”)” \boldsymbol{M}_{AA}, which have the two properties (following the definition in section 5.1 in (Bartusek, “Affine determinant programs”)):
-
(Correctness) For all \boldsymbol{x} \in \{0,1\}^n, Pr[det(\boldsymbol{M}_{AA}(\boldsymbol{x}))=0]=1.
-
(Rejection of Invalid Inputs) For all non-binary \boldsymbol{x} \in \mathbb{F}_p^n \setminus \{0,1\}^n, \ Pr[det(\boldsymbol{M}_{AA}(\boldsymbol{x}))=0]=negl(\lambda).
Using the All-Accept ADP, the ciphertext is built as the following ADP, which is mentioned as a generic candidate in section 5.2 in (Bartusek, “Affine determinant programs”).
\boldsymbol{M}_{\boldsymbol{h},\ell,b} :=
\boldsymbol{M}_{AA} + \boldsymbol{M}_{\boldsymbol{h},\ell} + (b\boldsymbol{S},0,\dots,0)
For any non-binary input \boldsymbol{x} \in \mathbb{F}_p^n \setminus \{0,1\}^n, det(\boldsymbol{M}_{\boldsymbol{h},\ell,b}(\boldsymbol{x})) \neq 0 holds since \boldsymbol{M}_{AA}(\boldsymbol{x}) is full-rank except with negligible probability. The determinant, therefore, outputs 0 iff b=0 and a valid witness \boldsymbol{w} \in \{0,1\}^n is provided.
In this way, the ADP is helpful to construct the WE scheme for the subset sum language as described in (Bartusek, “Affine determinant programs”). Note that the above explanation only covers the generic candidate. Strictly speaking, the ADP-based WE scheme is constructed for a "vector subset sum language in (Bartusek, “Affine determinant programs”), which is the generalization of the subset sum language. In the analysis of the efficiency described in Appendix, we assume the concrete candidate defined in section 5.2 in (Bartusek, “Affine determinant programs”).
Analysis of the ADP-based Witness Encryption
Based on the concrete candidate in section 5.2 of (Bartusek, “Affine determinant programs”), we analyze the size of the ciphertext and the complexity of the encryption/decryption. In the following description, m,k denotes the number of variables and clauses in the 3-SAT formula respectively, n denotes the number of wights in the instance of the subset sum language, p denotes the order chosen in the WE.Enc algorithm.
The size of the ciphertext grows with \mathcal{O}([\log_2 p]n^{3+2\epsilon}). The ciphertext \boldsymbol{M} consists of 2n+1 matrices over \mathbb{F}_p, and their each dimension is (2n^{1+\epsilon}+1) \times (2n^{1+\epsilon}+1). The size is, therefore, [\log_2 p] \times (2n+1) \times (2n^{1+\epsilon}+1)^2=[\log_2 p](8n^{3+2\epsilon}+4n^{2+2\epsilon}+8n^{2+\epsilon}+4n^{1+\epsilon}+2n+1) bits.
With m and k, the growth of the size is also represented as \mathcal{O}((m+k)^{4+2\epsilon}). It is well known that the 3-SAT formula with m variables and k clauses is reduced to the instance of the subset sum language with 2m+2k weights (Eva Tardos, “Reduction from 3 SAT to MAX CUT”). Replacing n with 2m+2k, the number of elements over \mathbb{F}_p in the ciphertext is 2^{6+2\epsilon}(m+k)^{3+2\epsilon}+(2^{4+2\epsilon}+2^{5+\epsilon})(m+k)^{2+2\epsilon}+2^{3+\epsilon}(m+k)^{1+\epsilon}+2^{2}(m+k)+1.
Each weight of the instance requires (m+k)[\log_2 10] bits (Eva Tardos, “Reduction from 3 SAT to MAX CUT”), so that the minimum size of p satisfying p>\max_{\boldsymbol{x}\in \{0,1\}^{2m+2k}}|\sum_i x_i h_i| is 1+[\log_2(m+k)]+(m+k)[\log_2 10] bits. Hence, the size of the ciphertext is \{(m+k)[\log_2 10]+[\log_2(m+k)]+1\}\{2^{6+2\epsilon}(m+k)^{3+2\epsilon}+(2^{4+2\epsilon}+2^{5+\epsilon})(m+k)^{2+2\epsilon}+2^{3+\epsilon}(m+k)^{1+\epsilon}+2^{2}(m+k)+1\} bits, whose order is \mathcal{O}((m+k)^{4+2\epsilon}).
The WE.Enc algorithm includes four types of computations whose complexities depend on n, that is, random sampling over \mathbb{F}_p, matrix addition, scalar multiplication, and matrix multiplication. The number of sampled elements in \mathbb{F}_p is
4\times 2n(2n^{1+\epsilon}+1)n^{\epsilon}+4n^2+(n+2)(2n^{1+\epsilon}+1)^2=4n^{3+2\epsilon}+24n^{2+2\epsilon}+4n^{2+\epsilon}+4n^2+16n^{1+\epsilon}+n+2. The addition between (2n^{1+\epsilon}+1) \times (2n^{1+\epsilon}+1) matrices is computed 4n^2+8n+1 times in total. The matrices are multiplied by scalars 4n^2+n+1 times if b=0, and 4n^2+n+2 times if b=1. The number of times of the multiplication between (2n^{1+\epsilon}+1) \times n^{\epsilon} matrices is 6n.
The WE.Dec algorithm consists of the computation of the affine function \boldsymbol{M}, and its determinant calculation. By the definition of the ADP, the former requires n-times matrix additions and n-times scalar multiplications.
References
[1] Bartusek, J., Ishai, Y., Jain, A., Ma, F., Sahai, A., & Zhandry, M. (2020). Affine determinant programs: A framework for obfuscation and witness encryption. In 11th innovations in theoretical computer science conference (itcs 2020).
[2] Gavin Uberti, Kevin Luo, Oliver Cheng, Wittmann Goh December, Building Usable Witness Encryption 10, 2021
[3] Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2018). Scalable, trans-parent, and post-quantum secure computational integrity. IACR Cryptol. ePrint Arch., 2018, 46.
[4] Gabizon, A., Williamson, Z. J., & Ciobotaru, O. (2019). Plonk: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge. IACR Cryptol. ePrint Arch., 2019, 953.
[5] Garg, S., Gentry, C., Sahai, A., & Waters, B. (2013). Witness encryption and its applications. In Proceedings of the forty-fifth annual acm symposium on theory of computing (pp. 467–476).
[6] Goldwasser, S., Kalai, Y. T., Popa, R. A., Vaikuntanathan, V., & Zeldovich, N. (2013). How to run turing machines on encrypted data. In Annual cryptology conference (pp. 536–553).
[7] Groth, J. (2016). On the size of pairing-based non-interactive arguments. In Annual international conference on the theory and applications of cryptographic techniques (pp. 305–326).
[8] Script bitcoin wiki. (n.d.). Script - Bitcoin Wiki. ((Accessed on 09/10/2021))
[9] Tardos, E. (n.d.). Reduction from 3 sat to max cut.
https://www.cs.cornell.edu/courses/cs4820/2015sp/notes/reduction-subsetsum.pdf. ((Accessed on 10/22/2021))
[10] Wrapped bitcoin ( wbtc ) an erc20 token backed 1:1 with bitcoin.* (n.d.).
https://wbtc.network/. ((Accessed on 11/17/2021))