One of the challenges of the CLR subsidy formula (if a set of agents i \in [1..n] each make contributions c_{i \rightarrow p} to a project p then the project p gets a subsidy of k * [(\sum_{i=1}^n \sqrt{c_{i \rightarrow p}})^2 - \sum_{i=1}^n c_{i \rightarrow p}] where k is the CLR subsidy coefficient) is that it assumes that agents are fully uncoordinated, and there are no bounds on how much money can be illicitly extracted from a CLR if even two agents are capable of coordinating: for any subsidy coefficient k, if two agents each put in a large amount of money M into a fake “project” that splits the funds between them, then they get a subsidy of k * [(2\sqrt{M})^2 - 2M] = 2cM. If k is set to target a fixed subsidy amount, then as M \rightarrow \infty the two agents would extract almost the entire subsidy and leave all other contributors with near-zero.
We can make the CLR design more robust to the possibility of coordination between agents as follows. First, let’s philosophically reinterpret the existing CLR formula somewhat.
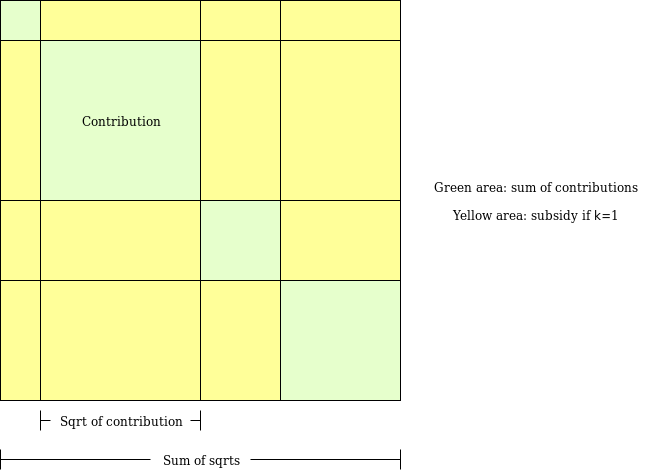
The green squares are the c_{i \rightarrow p} values, the sides of the squares are \sqrt{c_{i \rightarrow p}} values, the total green area is the original total contribution, and the yellow area is the subsidy if k=1 (the total size of the square is (\sum_{i=1}^n \sqrt{c_{i \rightarrow p}})^2, and the green area is \sum_{i=1}^n c_{i \rightarrow p}, so the yellow area is (\sum_{i=1}^n \sqrt{c_{i \rightarrow p}})^2 - \sum_{i=1}^n c_{i \rightarrow p}). But notice that we can reinterpret the area as being the sum of the sizes of rectangles, where each rectangle is of size \sqrt{c_{i \rightarrow p}} * \sqrt{c_{j \rightarrow p}} for all ordered pairs i \ne j (note that the (i,j) and (j,i) cases are identical so we can think of it as a subsidy of 2\sqrt{c_{i \rightarrow p}}\sqrt{c_{j \rightarrow p}} per unordered pair).
We can think of this as a pairwise coordination subsidy: for each pair of agents (i, j), if agent i contributed to a project that agent j also contributed to, then that means that agent i contributed to something that benefits agent j, and so agent i should be rewarded for this good deed. In the CLR formula, the subsidy given to each pair is k_{i,j} * 2\sqrt{c_{i \rightarrow p}}\sqrt{c_{j \rightarrow p}}, where k_{i,j} can be viewed as a “discoordination coefficient” for that pair: if k_{i,j}=1 then the pair is fully uncoordinated, if k_{i,j}=0 then the pair is fully coordinated and so the optimal subsidy is zero as the pair is itself fully capable of internalizing gains from coordination, but we could also have some 0 < k_{i,j} < 1.
The new idea here is that instead of a single global k value, we have a local k_{i,j} value for each pair of agents, and we make an assumption that the amount of funds a specific pair of agents put toward the same projects is itself evidence of how coordinated they are, and so the more total funds a pair of agents put toward the same projects, the lower we set the k_{i,j} value for that pair.
Let us try a coefficient k_{i,j} = \frac{M}{M + \sum_p \sqrt{c_{i \rightarrow p}}\sqrt{c_{j \rightarrow p}}}, where M is a tweakable parameter. That is, k_{i,j} = \frac{M}{M + T} where T is a measure of the total extent to which participants i and j both contribute to the same projects (the sum \sum_p is summing over all projects). So the more that any two agents i and j are seen to coordinate in general, the lower a subsidy coefficient k_{i,j} we give to that particular pair.
Now, let’s suppose that k coordinated agents all contribute a very large amount of money W (think W \rightarrow \infty) toward a project. There are \frac{k * (k-1)}{2} pairs, and in each pair the coefficient k_{i,j} is \frac{M}{M + W}, so the subsidy that they can extract is k_{i,j} * 2\sqrt{W}\sqrt{W} = \frac{2MW}{M + W} < 2M.
Hence, the new scheme offers a clear bound (k * (k-1) * M) on the amount that the system loses to unexpected coordination between k agents (which could come completely illegitimately, eg. fake accounts, or more benignly, as in two people from the same family caring about each other). The emphasis of the CLR switches from assuming total non-coordination between individuals to being more robust against there being some level of existing coordination between individuals, and focusing on subsidizing coordination between individuals who would not normally coordinate.
If one wishes to set up subsidies to target a particular level of total expenditure (ie. target \sum_{p \in projects} \sum_{i=1}^N \sum_{j=1}^{i-1} f(c_{i \rightarrow p},c_{j \rightarrow p}) = T), one can adjust the value of M to do so. If M = 0 then T = 0, if M \rightarrow \infty then T will almost always be too high, so one can binary-search M to lead to the desired total T.
Another possible future direction is distinct M values for each agent pair, where M_{i,j} = M_i * M_j, where each M_i is set based on a measurement of how certain we are that some given agent actually is a unique individual (ie. accounts that pass lower levels of verification would see lower M_i values).