PeerDAS with significantly less bandwidth consumption

Networking
, ,
1

Authors: pop

tldr; this proposal reduces the bandwidth consumption of PeerDAS by 56.2%

Currently GossipSub imposes an amplification factor on the bandwidth consumption to PeerDAS, since more than one peers can send you the same columns. In fact, you need only one copy, so this amplification wastes your bandwidth.

Previously we have IDONTWANT implemented which reduces the number of copies you will receive, but it doesn’t guarantee exactly how many.

This proposal enables nodes to receive only one copy of most of their sampled columns.

Current bandwidth consumption

(For simplicity, let’s assume that DATA_COLUMN_SIDECAR_SUBNET_COUNT and NUMBER_OF_CUSTODY_GROUPS are equal to NUMBER_OF_COLUMNS)

Let S be SAMPLES_PER_SLOT, C be the size of a column, and D be the amplification factor of GossipSub (aka the mesh degree).

Nodes are required to subscribe to and sample S columns, so each node has to consume the bandwidth about D*S*C bytes per slot.

New design

Previously, we have each node subscribe to S GossipSub topics. Now, we subscribe to fewer topics than that. We have each node subscribe to K=2 topics which is lower than S. Nodes will still receive or forward D copies in these K topics, but they will receive only one copy and forward no copy for the remaining S-K topics.

The reason that we still need to subscribe to K topics is because we need to provide backbones for the topics as required by topic observations (aka stability of the topics).

The bandwidth consumption of K subscriptions is D*K*C bytes per slot.

slot-breakdown
slot-breakdown1589×485 41.2 KB

Now, the remaining question is how the node can get the remaining S-K columns that it needs.

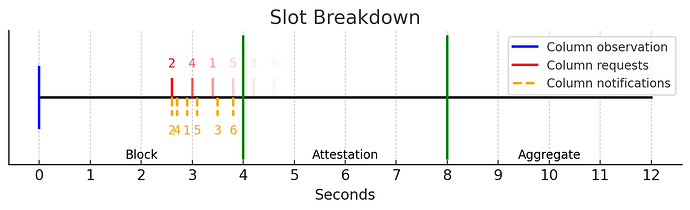
Firstly, you start observing the topic at the beginning of the slot (shown as a blue line).

After that, your peers will notify you when there is a new message in the topic. Orange lines show when your peers notify you. Notice that peer 2 is the first one who gets the message (column) and notifies you first.

Since peer 2 notifies you first, you request the actual column from peer 2 with the timeout T (400 ms). After the timeout, if you don’t get it from peer 2, you request it from the peer that notifies you second which is peer 4. If you still don’t get it, you keep going on. Red lines show when you request the column from each peer. The further lines are lighter to indicate that it’s less probable. Consecutive lines are 400ms apart indicating the timeout.

It looks like timeouts will delay the column reception a lot because with the current PeerDAS you will get the column right at the orange lines which are faster. In fact, it’s not that bad for the following reasons.

  1. It saves a lot of bandwidth. Imagine that you get a copy of the column at each orange line. That looks very wasteful. With this proposal, you get only one copy at one of the red lines.
  2. Timeouts are rare. You don’t expect to get many timeouts for the following reasons.
    • The network condition is already good. If not, how could your peer notify you that it gets a message?. If you could notify me, so you could also send me the column. If it doesn’t, you can probably de-score it.
    • Your peer can send you an early rejection without waiting for the timeout. For instance, if your peer is overloaded and doesn’t want to waste the bandwidth sending you the column, it can just send a rejection to you and you can move forward to another peer quickly.

New bandwidth consumption

  • The bandwidth consumption due to subscribing to K topics is D*K*C bytes per slot.
  • The bandwidth consumption due to observing and downloading the remaining S-K columns is (S-K)*C bytes per slot.
  • The bandwidth consumption due to sending the columns to observing peers is the same as above which is (S-K)*C bytes per slot.

The total bandwidth consumption would be (D*K+2*(S-K))*C bytes per slot.

Assign the parameters with the current assignments in the spec: D = 8, K = 2, and S = 8.

  • The bandwidth consumption of the current PeerDAS is 64*C.
  • The bandwidth consumption of the new one is 28*C which is 56.2% reduction.

The reason I assign K=2 is because, with 8k nodes and the number of columns of 128, there will be at least 100 nodes in each topic.

Pessimistically, if you think K=2 doesn’t make the topics stable enough, we can go to K=4 and the bandwidth consumption would be 40*C which is still 37.5% reduction.

Comparison to IDONTWANT

You can note that the analysis in the previous sections assumes that you will receive or forward exactly D copies of messages when subscribing to topics.

This is not true with IDONTWANT since it can reduce the number of copies you will receive by sending IDONTWANT to your peers before they send you a copy.

There is a still corner case that IDONTWANT doesn’t help reduce the number of copies at all. Imagine that all of your peers send you the message at the same time (the orange lines are very close to each other), so you don’t have a chance to send IDONTWANT to them in time. So, in this case, you still receive the same number of copies as before. While in this proposal, it’s guaranteed that you will receive only one copy.

However, we can combine this proposal with IDONTWANT to get an even better protocol. Since nodes still subscribe to K topics. IDONTWANT can reduce a lot of bandwidth consumption there.

Comparison to Peer Sampling

Peer sampling is a process that after all the columns are disseminated through the network, you request a column from your peer that’s supposed to have it. If you get the column back, it means that column is available. If not, you may either request another peer or decide that the column is not available.

You can see that you always request for a column no matter what which is different from this proposal. In this proposal, you will request a column only if your peer notifies you that it has one. So peer sampling and this proposal are fundamentally different.

Another difference is, in peer sampling, you aren’t sure when to request a column. In other words, you don’t know when the column dissemination is finished so that you can start requesting the column. What you can do is to set an exact timestamp that you will assume the dissemination is already finished and start requesting. This sometimes waste you some time since the dissemination is finished far before the timestamp. In this proposal, you don’t get this problem since you’re notified when you can request.

2

It is a nice proposal.

I still think K=2 is quite optimistic and only considers the happy case. When the network is not behaving well, that backbone might not be robust/fast enough, and you might start getting the notifications (orange lines) well past your deadline. A more conservative approach would be to start with K=4 and make simulations/experiments to evaluate if this is robust enough to tolerate large correlated failures.

Also, in the case K=4 and 43% bandwidth reduction, how does this compare to using only IDONTWANTs. It seems to me that if the network is very efficient, then IDONTWANTs do not help much, but if the network has small inefficiencies, IDONTWANTs do help because there is more “space” between arrivals.

3

Do you have any criteria or formula in mind to determine what K should be? My criteria is that there should be at least 100 nodes in each topic. (I’m trying to make this less subjective)

How can having more nodes in the topic make the propagation faster? That’s counter-intuitive to me. If the number of nodes go higher while the degree is still the same, the basic graph theory tells that you will need more hops to propagate a message.

The bandwidth and geolocation(implying latency) of nodes are indifferent because nodes in topics are random so you can expect the same bandwidth resource of each individual node as when K goes higher.

In conclusion, the network is faster with less K.

Now let’s talk about what robustness means. When K goes low, the implication is the number of nodes in the topic goes low and why is it a problem when it goes low?

Because graph theory tells that when the degree is the same and the number of nodes goes lower, it’s more likely to have a network partition (the graph is unconnected).

And when we have a network partition, when some node publishes, some node may not get the message.

That’s the only problem with stability (robustness).

My rule of thumb is always to have at 100 nodes in each topic (which is subjective of course).

I changed the number to 37.5% because I had some small miscalculation. Sorry about that.

I don’t know what the number is compared to using only IDONTWANTs, but that question doesn’t matter right? because combining this proposal with IDONTWANTs we will have better bandwidth consumption anyway.

Let’s say using IDONTWANTs save X% of bandwidth, using only IDONTWANTs will consume (1-X/100)*D*S*C bytes per slot.

If we combine this proposal with IDONTWANTs, it will consume ((1-X/100)*D∗K+2∗(S−K))∗C bytes per slot which is always less than using only IDONTWANTs anyway because (1-X/100)*D cannot go lower than 2.

One advantage of this proposal over using only IDONTWANTs is that this proposal definitely reduces bandwidth consumption while using only IDONTWANTs depends on the efficiency you mentioned.

4

Because graph theory tells that when the degree is the same and the number of nodes goes lower, it’s more likely to have a network partition (the graph is unconnected).

Network partition is the worst case, but you could also have a connected network where data takes more time to propagate because you need to do more hops given that part of the nodes are down. Take, for example, the figure in your Topic Observation post, and imagine you want to propagate data from node 2 to node 9, but nodes 7 and 8 are down, in those conditions data will need to do three hops instead of two. That is what I meant when I mentioned a decrease in speed if K is too low. If K is larger, you have more mesh connections (e.g., a direct connection between nodes 9 and 1) that still provide some robustness.

Do you have any criteria or formula in mind to determine what K should be?

This is a good question. I think one way to approach this is to start by determining the worst attack we want the network to be able to withstand and then derive the network parameters from there.

5

While this looks like a good optimization I would be careful with it as it changes security properties which may significantly differ from the approach considered at the moment.
The current approach mostly relies on subnet sampling while this optimization is more like a hybrid peer/subnet sampling (tending more to peer sampling).
From my perspective peer sampling has significant security flaw and is vulnerable to a simple attack which results in false-positive sampling (here are some thoughts on this: Peer Sampling thoughts - HackMD)

6

And also as @leobago mentioned it makes subnet backbones thinner (basically 4 times thinner) which is a different security impact to consider

7

In fact, the main point of this proposal is that the backbone of the current PeerDAS is too thick and there is no way to customize that because everyone is supposed to subscribe to S topics and not less than that without losing fork-choice security.

This proposal allows us to customize the thickness of the backbone (by changing K) without touching S. The question is how thick should the backbone be. Either K=2 or K=4, we still have a significant reduction.

K=8 is obviously too thick. It’s like you have 8k/(128/8) = 500 nodes per topic. Image that you have 16 attestation subnets rather than 64.

8

That doesn’t sound like a fair comparison.

If your peers are down, you are supposed to find other peers to keep your degree to the expected number and those new peers will keep the hop count low, so the increased number of hops doesn’t make any sense.

But never mind, let’s say somehow you cannot find new peers or cannot find them in time, the statement that the lower K is slower than the higher K still doesn’t make any sense.

For the failure mode, if K is

  • Low, the number of hops increases when some nodes are down. That’s is true, but if K is
  • High, the number of hops also increases given that the percentage of failed nodes is the same. (not sure how much, but it does)

So how are you sure that the number of hops is higher, when K is lower?

For the non-failure mode, the number of hops of lower K is absolutely lower than higher K.

In fact, I can make a mathematical reasoning that the failure mode is in fact equivalent to the non-failure mode, so even in the failure mode, the number of hops of lower K is also lower than higher K, given that the percentage of failed nodes and links is the same.

Let’s say the number of nodes in the lower-K topic is N_1 and the number of nodes in the higher-K topic is N_2.

Since the degree of each node is D in both networks, the numbers of links in both networks are O(N_1*D) and O(N_2*D) correspondingly. When a fraction F of links are down in both networks, the numbers of links now become O((1-F)*N_1*D) and O((1-F)*N_2*D). This means that the degree of each node in both networks after removing the failed links becomes O((1-F)*N_1*D/N_1) = O((1-F)*D) = O((1-F)*N_2*D/N_2) which is the same for both networks.

Accounting for the failed nodes is trivial, so I will skip it.

So the failure mode is just equivalent to the non-failure mode with just lower degree and lower number of nodes.

So lower-K is always faster than higher-K no matter what

9

So lower-K is always faster than higher-K no matter what

Let’s take it to the extremes and see if your logic holds, two cases:

  1. K = N (the size of the network), so everyone is directly connected to everyone; just one hop for any communication.

  2. K = 2, basically a virtual ring. In the worst case, the communication between two nodes is half of the ring, so N/2 hops.

Am I missing something here?

10

K is supposed to be less than or equal to S, so K = N doesn’t make any sense.

That’s impossible. Everyone is supposed to connect to only D other peers.

I see. I think you misunderstood K as D.

11

I was taking extreme cases as examples, if D = N (which is obviously not practical) then you could have K = D = N.

Anyway, I think this is not converging.

I disagree with the idea that lower K is always faster.
I agree lower K saves bandwidth.

Experiments and simulations will be necessary to demonstrate how much.

12

D = N is not even how gossipsub is supposed to work. K > S doesn’t make any sense.

K has a unit as the number of topics. K = N doesn’t make any sense. Like we have only NUMBER_OF_COLUMNS = 128 topics. Let’s say the number of nodes is 10k.

Saying K = N is equivalent to saying let’s subscribe to 10k topics where we have only 128 topics.

13

It’s a questionable statement. Small subnet could be pretty vulnerable for sybil/eclipse attack. The question is how many column subnets need to be attacked (when no message could be propagated within this subnet) to disrupt the network?

E.g. for attestations 1/3 of all subnets need to be under attack to prevent finality. Attacking a single subnet would just result in 1/64 participation drop. So this doesn’t look catastrophic for the network.

The interesting question is what would be effect of attacking 1 or more column subnet?

14

That’s an interesting question.

In order for a node to cast a vote, it has to receive all 8 columns.

At least 2/3 of validators has to vote to make the network live for finality. Let’s say the attacker can attack X column subnets.

The probability that a node will receives all 8 columns is {128-X \choose 8}/{128 \choose 8}, so the following must holds to be live. {128-X \choose 8}/{128 \choose 8} > 2/3

Now you get X \leq 6

So the answer is the attacker has to attack 7 column subnets to prevent 1/3 of validators from voting. While you need to attack 21 attestation subnets to achieve the same effect.

Yeah, you are right, the column subnets are more susceptible.