by U. Natale.
Acknowledgements
This research has been granted by Chorus One. We are grateful to M. Moser, B. Crain, and Y. Socolov for useful discussions and comments. We also thanks J. Bostoen and F. Mosterts from Chainbound team for reviewing the entire document (review ≠ endorsement).
Preconfirmations landscape
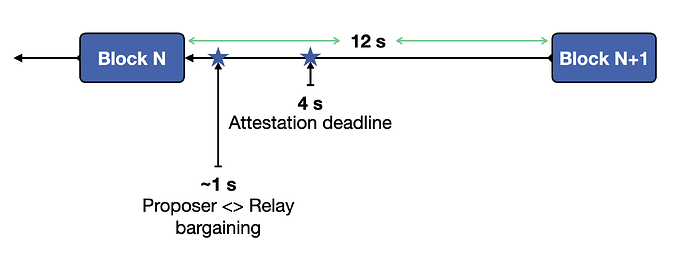
In the context of PBS, bargaining between proposer and relay start at around 1s. This means that users submitting transactions after 1s have to wait for the next slot to know if the transaction is included or not. Even in the context of timing games and assuming some aggressive player, there is a hard cut-off at < 4s due to attestation deadline.
Fig. 1: The current setup under PBS.
With preconfirmation, users have the possibility to access the dead time space between two blocks via a credible heads-up before a confirmation happens. However, at the moment, preconfirmations give no guarantees on execution.
For example, imagine 2 users submit 2 conflicting transactions (e.g. a swap against the same pool), but both get a preconfirmation. What happens in slot N+1 is that both transactions land in some place into the slot, but one of the two fails.
From the provider of preconfirmations perspective, the original agreement was respected, however one of the two users next time will think twice before paying for a preconfirmation. The same scenario can happen even if there is only one preconf, but this transaction lands in some place into the slot after other conflicting transactions.
This poses some questions on who can preconfirm a transaction and who can’t. From the two example above it is evident that unsophisticated players can’t play this game and provide a real improvement for the Ethereum ecosystem. It is clear that the burden would be reduced if the preconfs were intended only for transactions that do not touch contentious state — e.g. transfers of tokens and NFTs, dApps with “batching” architecture, L2 settlements, etc. In this case no sophistication is needed so we will exclude it from the goal of this analysis.
Proposer as preconf provider
Preconfirmations should be managed in a manner which is similarly decentralized to the current PBS setup; they should not give rise to a centralization bottleneck that exceeds the current builder dominance.
Fundamentally, the PBS transaction pipeline is an auction. Preconfirmations under a gateway architecture follow a delegation scheme, where node operators (NOs) select a third party to select transactions for future inclusion. Therefore, the gateway design is not a spot market, and a generally less competitive scheme as the cost of switching is considerably higher. Indeed, the gateway architecture expects each validator to sign an on-chain transaction to deposit collateral, meanwhile this operation under PBS is done completely off-chain, meaning that there is no cost to switching builders.
This may directly reflect in multi-block MEV, where gateways will be able to provide increasingly more competitive partnership offers to node operators as they scale their dominance over the network. In difference to PBS builders, these gateways will have certainty over the slots for which they hold a mandate. Therefore, a gateway architecture is likely to manifest as a heavily centralized setup, where multi-block MEV is the central return to scale, and switching costs are high. Overall, as it is not an auction or a spot market, the gateway architecture is more likely to manifest a centralization bottleneck which exceeds PBS builder dominance.
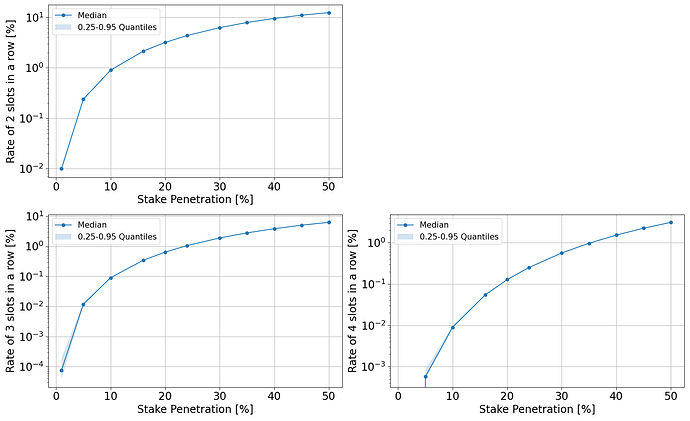
Fig. 2: Rate of N slots in a row over total Ethereum slots in a year as a function of stake penetration. Growth is higher than linear, and the case of builders/gateways dominance in block production is just an extension of above.
A preferable scheme would be the proposer selecting preconfirmations itself. Even in the case of the largest proposers, their ability to engage in multi-block MEV is capped by their voting power (see Fig. 2), which is in turn is capped by the proposer market (i.e. access to capital). Even under PBS, proposers could theoretically already engage in multi-block MEV, but refrain to do so, for a variety of reasons ranging from access to capital and organisational setup, to legal liability. These same patterns would likely extend to a preconfirmation setup.
In this section we are going to analyze some scenarios that may arise if the proposer of the slot is the one providing preconfirmation for transactions. We further assume that the NO is a sophisticated player, since the more transactions an unsophisticated preconfirmations provider includes in the preconfirmation list, the more difficult it is for block builders to create a block with all transactions being successful. This implies an execution guarantee on preconfirmed transactions.
If the majority of preconfirmed transactions fail, the market becomes less attractive, making preconfirmations a difficult tool to use. Including conflicting transactions can also damage the NOs credibility, negatively impacting the brand.
Information edge from private order flow
In this section we are going to show the different information edge builders have in the current PBS framework. As we did in The cost of artificial latency in the PBS context, we can define a standardized parameter that allows for a comparison of bids irrespective of their absolute size. This corresponds to the ratio between a given bid and the maximum bid in the auction for a particular slot. That is
where b is the bid value, s indicate the corresponding slot, and t_E is the time at which the bid was made eligible. This allows us to compare builders bidding strategy over all slot proposed by Chorus One since 2024-03-13.
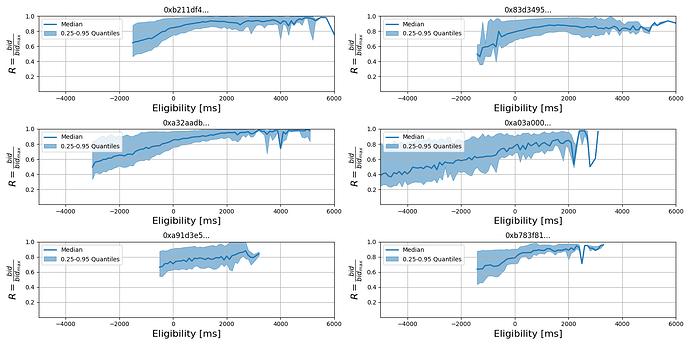
Fig. 3: Builder bidding strategy standardized over all slots proposed by Chorus One since 2024-03-13.
If we select 6 of the top builders by entity (according to mevboost.pic), we can clearly see a difference in the overall strategy, see Fig. 3. For example, we can see how some builders start to deliver bids “late” into the slot, others seems to start much earlier. Furthermore, some builders have a clear linear trend in bid increase per unit of time, others seems to start being careful near the end of the auction.
Although this is independent from the information edge coming from private order flow, we can see how different builders propagates different values of R. Precisely, at 1s into the slot (that is the median value for bid selection in current PBS framework) we have
- Builder: 0xb211df4…, Median: 0.91, 0.25-quantile: 0.83, 0.95-quantile: 0.99
- Builder: 0x83d3495…, Median: 0.86, 0.25-quantile: 0.75, 0.95-quantile: 0.97
- Builder: 0xa32aadb…, Median: 0.90, 0.25-quantile: 0.83, 0.95-quantile: 0.98
- Builder: 0xa03a000…, Median: 0.81, 0.25-quantile: 0.74, 0.95-quantile: 0.95
- Builder: 0xa91d3e5…, Median: 0.79, 0.25-quantile: 0.65, 0.95-quantile: 0.93
- Builder: 0xb783f81…, Median: 0.88, 0.25-quantile: 0.82, 0.95-quantile: 0.96
that indicates how different entities arrive to the most-likely-end of the auction with less/higher bid values.
From the NO perspective, a difference in information edge could lead to a mispricing of MEV txs, thus increasing the risk of producing less valuable blocks. In general, builders in the current MEV-Boost framework have a comprehensive view of all transactions and typically include those that maximize the block value. However, with validators as preconfirmation providers, proposers must select transactions in advance, often without knowledge of transactions occurring on private channels. The primary metric available to validators in this scenario is the base fee. Specifically, if a transaction pays the base fee (BF) plus a priority fee (PF), it is considered valid in principle. But if the priority fee is the lowest compared to transactions in the private order flow from builders, the block value could decrease. This is because builders are now required to include the preconfirmed transaction instead of a potentially more valuable one. Here sophisticated NOs are in advance since they can develop models to probabilistically evaluate transactions and perform an opinionated selection.
It is worth noting, that validators with private transaction flows could be incompatible with preconfirmations, depending on implementation. Private transaction flows can also manifest by virtue of network jitter. Indeed, if a proposer gives a preconfirmation on a transaction from private transaction flow (or on a transaction from an RPC that’s close to the proposer, but far away from the builder), there could be a non-zero likelihood this transaction is not known by the builders, which may find it difficult to build a valid block (i.e. with the preconfirmed tx). The solution is that the proposer sends the full transaction to builders. Concerns about privacy are clearly excluded since the proposer already committed to certain execution, and the builder can’t really do anything about that.
Enforced early timing-games
Arbitrageurs often engage in short-term trading due to competitive pressures. When they opt to delay immediate gains in hopes of capturing a greater mispricing, they run the risk of losing the lucrative opportunity to other traders. This issue is particularly critical within Ethereum’s Proposer-Builder Separation (PBS) mechanism, where searchers must strategically balance their bidding approaches.
Consider an arbitrage opportunity that arises relative to an external source, such as a centralized exchange (CEX), at t=4 seconds into slot N. Since the on-chain price is stale and searchers are uncertain whether the opportunity will vanish on the CEX side, they may prefer to execute the first leg of the trade on the CEX immediately and wait the canonical 12 seconds to see their transaction confirmed on-chain. In the PBS context, however, if a searcher immediately bids their maximum willingness to pay for the opportunity, there is a non-zero likelihood that other searchers may outbid them, effectively frontrunning the original strategy. Conversely, if the searcher bids aggressively too late, the closing trade may fail to be included on-chain since the proposer has already committed to a block that excludes this particular transaction. This scenario creates an auction dynamic that hinges on accurately pricing the time within the slot. The same applies for a DEX <> DEX opportunity, since other arbitrageurs may offer a higher share of MEV for the same opportunity and then seeing their bundle being selected.
Therefore, searchers must strategize not only about how much to bid, but also about the optimal timing of their bids. Bidding too early or too late can both result in a loss of the arbitrage opportunity. The delicate balance between these factors is crucial for optimizing their strategies in such competitive and time-sensitive environments. This study models this behavior and evaluates various strategies to understand the optimal bidding dynamics in Ethereum’s PBS framework.
Model Description
To investigate how the introduction of preconfirmations might influence the auction dynamics in PBS, we conducted simulations using an Agent-Based Modeling (ABM) framework. The model is designed to simulate the behavior of searchers participating in PBS auctions under varying conditions, incorporating elements of competitive bidding and strategic timing. In our model, we assume that searchers at step N are aware of the bids at step N-1. While this might seem at odds with the usual dynamics in MEV-Boost, where the auction is not publicly visible, we can reconcile this assumption with two scenarios:
- Historical Data Adjustment: Searchers adjust their bidding strategies based on the share of MEV extracted as a function of past data. In this scenario, at each step N, searchers are informed about the behavior of searchers at the corresponding step N-1 from the previous slot. Thus, the predictive model is grounded in the historical data of past auctions.
- Vertically Integrated Builders: In this scenario, searchers are considered as vertically integrated builders. Here, we can imagine a block as a composition of transactions that produce a certain value for the MEV, with the bidding phase representing the exact competition between builders.
By incorporating these scenarios, our model aims to provide a simplistic but comprehensive understanding of how searchers might operate within the PBS auction mechanism under the influence of preconfirmations.
Searchers behaviour
In the model, each agent represents a searcher with a specific profit margin, aggressivity parameter, and fear-of-missing-out (FOMO) factor. These agents operate in a simulated environment that mimics the Ethereum PBS auction mechanism. Each agent’s decision-making process is influenced by the bids placed in previous auction steps, representing the competitive nature of the environment.
Agents update their bids in each step based on a combination of their internal parameters and the observed bids from the previous step. The bid update process is governed by a logistic growth model, where the increment of the bid follows a logistic function, adjusted by the agent’s aggressivity parameter and FOMO factor. This approach ensures that agents increase their bids more cautiously in the early stages and more rapidly as the auction progresses, reflecting the strategic balance between the risk of being outbid and the urgency of capturing the arbitrage opportunity. This dynamic allows the agents to optimize their bidding strategies over time, aiming to reach the maximum bid value closer to the end of the auction period.
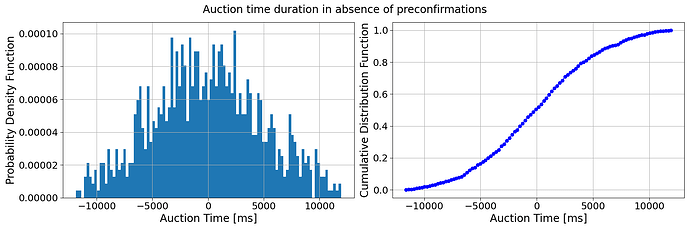
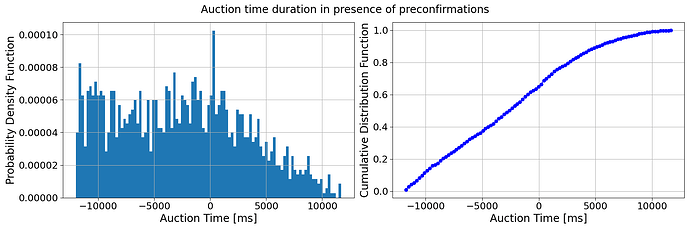
Additionally, agents take into account the probability that the auction may terminate at any given step. This probability is derived from a fictitious empirical distribution of auction durations, modelled using a truncated normal distribution to generate realistic auction durations, cfr. Fig. 4. In case of preconfirmation, we add a half-normal distribution to the previous one, cfr. Fig. 5. The termination probability influences the agents’ urgency in placing bids, as they must balance the risk of the auction ending unexpectedly with the potential benefits of waiting for a more opportune moment to bid. This probabilistic approach ensures that agents are not only competing against each other but also managing the inherent uncertainty of the auction’s duration.
Fig. 4: Single instances of a fictitious empirical distribution for the transaction selection time into the auction in the absence of preconfirmations.
Fig. 5: Single instances of a fictitious empirical distribution for the transaction selection time into the auction in the presence of preconfirmations.
The model incorporates four different types of searchers, each using a different predictive model to estimate the bid for the next step before applying their respective increment:
- Predictive Model 1: This model predicts the next bid as simply the maximum bid observed so far. It assumes that the current trend will continue without significant changes.
- Predictive Model 2: This model uses a linear regression based on the bid history to predict the next bid. It fits a linear model to the previous bids and uses the resulting slope and intercept to estimate the next bid. This approach assumes that the bid growth can be approximated by a linear trend.
- Predictive Model 3: This model calculates the average increment of the bids from previous steps and adds this average increment to the current maximum bid. This model assumes that past increments provide a good estimate for future increases.
- Predictive Model 4: This model uses a logarithmic fit based on the bid history to predict the next bid. It fits a logarithmic model to the previous bids and uses the resulting parameters to estimate the next bid. This approach assumes that the bid growth follows a decelerating trend, reflecting a more conservative strategy as the auction progresses.
By incorporating these diverse predictive models, the simulation captures a wide range of bidding behaviors and strategies, providing a more comprehensive understanding of how different types of searchers might operate within the Ethereum PBS auction mechanism.
Results
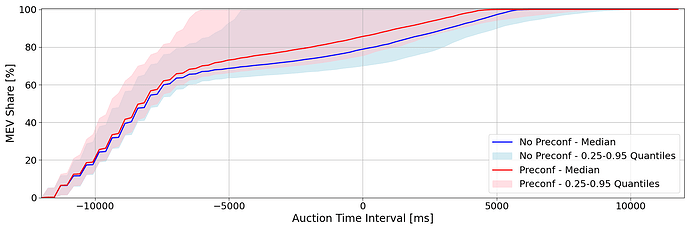
Analyzing the results in Fig. 6, we observe that in scenarios where preconfirmations on transactions are possible, searchers begin to increase their share of captured MEV earlier. This suggests that to increase MEV share received, a node operator might opt to run the version that allows for preconfirmations but never actually selects any MEV transactions. This creates a situation where searchers bid higher because the auction might end sooner. However, since no preconfirmations are offered (as the validator does not select any), the auction continues, and searchers find themselves starting from a higher base bid.
Fig. 6: Distribution of different bidding strategy extracted from a set of simulation using the ABM described in previous section. Simulations including a preconfirmation phase are in red, simulations without a preconfirmation phase are in blue.
This situation can be likened to a modified version of the prisoner’s dilemma. In this strategic game, each searcher (or prisoner) must decide whether to bid aggressively early (cooperate) or wait for a more opportune moment (defect). If all searchers bid aggressively early, they collectively drive up the MEV share and risk overbidding. Conversely, if they all wait, the auction proceeds normally, and they can potentially secure MEV shares at a lower cost. However, if some searchers bid aggressively while others wait, the aggressive bidders might secure a higher share early, pushing the late bidders to increase their bids even further as the auction continues.
This dynamic creates a tension between the searchers: each must decide whether to trust that others will not bid aggressively early or to secure their position by doing so themselves. The presence of preconfirmations adds an additional layer of complexity, as the threat of an early auction end prompts higher early bids, even when no actual preconfirmations are selected.
In summary, the introduction of preconfirmations influences searchers’ bidding behavior, leading to higher initial bids due to the perceived risk of an early auction end. This strategic interplay resembles the prisoner’s dilemma, where individual decisions to bid early or wait impact the collective outcome, highlighting the intricate balance between cooperation and competition in optimizing MEV shares.
In other words, with preconfirmations, searchers competing for the same opportunity can no longer rely on the probability that a certain builder will win a slot. If a competing searcher’s transaction is preconfirmed, even if the transaction is accepted by the winning builder, the builder must prioritize the preconfirmed one.
Reversal timing-game
Currently, the dynamics involve searchers relying on private auctions through builders, who have a certain probability of winning the block. Builders construct a block based on the privately received transactions and subsequently compete with other builders (through a public auction) to determine the winning block.
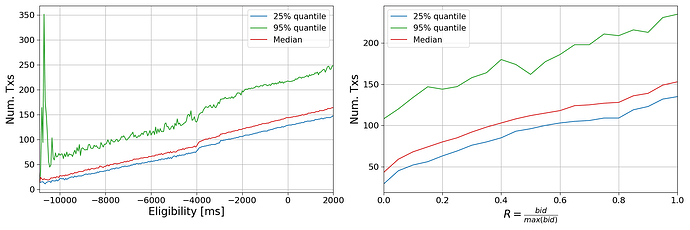
Fig. 7: Dependency in current auction dynamic between number of transactions included in the block and bid value, source from The cost of artificial latency in the PBS context.
Empirical data shows that the number of transactions included in blocks proposed by builders and the value of the block increase linearly, cfr. Fig 7 and [The cost of artificial latency in the PBS context](https://ethresear.ch/t/the-cost-of-artificial-latency-in-the-pbs-context/17847**.** This implies that once an arbitrage opportunity between CEX and DEX is identified, stat-arbitrageurs submit their transaction, which is not further modified, and the additional value builders obtain comes from a greater inclusion of transactions. In fact, searchers prefer to submit their transaction immediately as the opportunity might vanish on the CEX, and there is a form of preconfirmation due to the historical probability of a builder winning an auction. Therefore, it is highly likely that the rebalancing on the CEX occurs in the early stages of the block.
By modeling the price difference between CEX and DEX as a Markovian jump-diffusion process, we can derive the expression for the probability that searchers can execute a profitable trade (i.e. that the price difference is greater than the fees needed to execute the trade). This probability, P, is given by (see Appendix for a derivation):
where \gamma represents the fee of the trade, \lambda is such that the time mean interval between trades is \bar{t} = \lambda^{-1}, \sigma is the volatility of the price difference.
Equation (2) allows us to define a new dynamic for stat-arbs under the preconfirmation framework. Indeed, when the time interval between trades is small (i.e. high values of \lambda), the probability of having a profitable trade decrease. On the other hand, if volatility becomes predominant, the dynamic may change. Preconfirmations allows arbitrageurs to tune the time interval \lambda^{-1} in order to maximize the probability of being in the trading regime on a volatility based strategy.
Precisely, the time between trades is determined by the time at which the previous slot selected transactions and the time at which new transactions are selected for current block. With current PBS design this corresponds to 12s. Indeed, even if the builder knows he won the slot at t=4s into the slot N-1, he now has to wait 12s (i.e. 4s into the slot N) before knowing if he wins the slot N. With preconfirmations the frequency of transaction selections is a dynamic variable, because you know that your transaction is selected at different time wrt. the usual 4s into the slot. Clearly, by alternating preconfirmations with normal block inclusion, the parameter \lambda is non-constant.
If now the objective is to minimize the ratio \sqrt{2\lambda}/\sigma, if the volatility is low searchers can start to increase the frequency of trades submission (i.e. participate in preconfirmation auction) in order to maintain \sqrt{2\lambda}/\sigma << 1.
This modeling is consistent with the hypothesis that searchers may be interested in submit their transaction at the beginning of the block. This creates a dynamic potentially opposite to the timing games observed in the MEV-Boost context, where now searchers strive to compete from the early stages in the preconfirmation market.
Capturing on-chain MEV
With node operators as preconf provider, preconfirmations give validators the power back to decide on some transaction that have to be included in the slot. This means that NO can add new transactions on top of the current MEV-Boost pipeline, meaning that the ways of capturing MEV augment. Indeed, if we stay in the assumption that preconf transactions are likely to be executed as valid transactions, each time a validator is selected to propose a slot, it can preconf on his own transactions. This means that some types of on-chain MEV, in principle, can be captured by NO using preconfirmations, without renouncing to CEX <> DEX arbitrage, that might result more complicated for NOs.
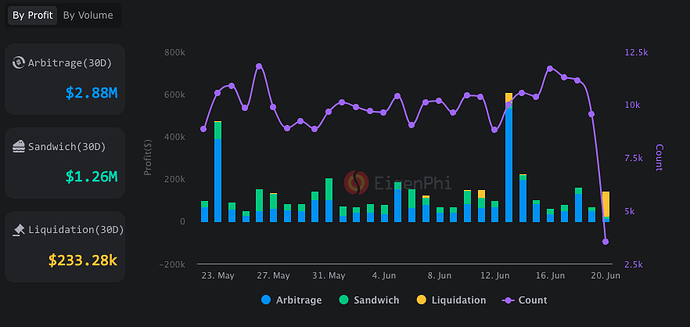
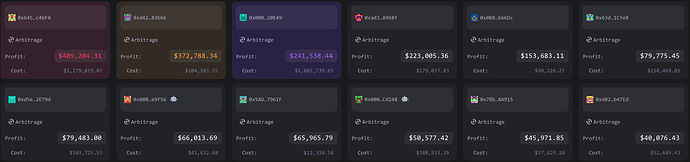
Fig. 8: Daily extracted MEV in 30 days by profit. Source EigenPhi.
Given the importance on the order of transaction execution, only arbitrage and liquidation could be captured using preconfirmation. According to EigenPhi, arbitrages and liquidations produced revenue of $3M profit in 30 days. From the Top 12 leaderboard on arbitrageurs, we can see that only 66% of captured MEV is shared with builders. Clearly, also builders retain a portion of MEV, but due to lack of data, we exclude this from our calculation, which at the end will provide a lower bound on extra revenue a NO can make.
Fig. 9: Leaderboard of top 12 on-chain arbitrageurs in 30 days. Source EigenPhi.
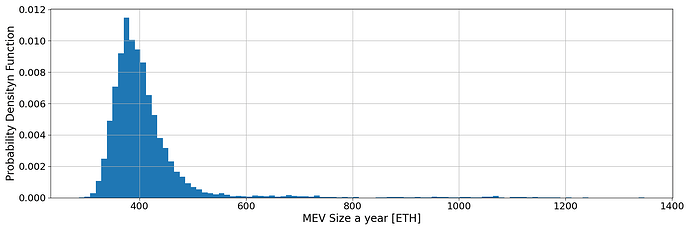
If we assume that a NO with 1% of stake penetration captures 1% of this extra MEV, there is an extra $345,600 in a year. Since the median MEV revenue for a NO with such share is ETH 392.31 (cfr. Fig. 10), assuming a price per ETH of $3,500 this (98.74 ETH extra MEV) corresponds to a 25.17% increase from MEV revenue in a year. It is worth mentioning that current timing games provide ~10% extra MEV.
Fig. 10: Probability Distribution Function of MEV proceeds in a year for a node operator with 1% of stake penetration.
Conclusions
Implementing a sophisticated system for preconfirmations within Ethereum’s PBS framework is far from trivial. This complexity opens new avenues for sophisticated NOs to enhance their revenues from MEV.
Our study has demonstrated that preconfirmations introduce a significant layer of strategic depth to the PBS auction mechanism. By providing searchers with a credible heads-up before a transaction is confirmed, preconfirmations alter the timing and aggressiveness of bids. This shift is particularly pronounced in scenarios where NOs, acting as preconfirmation providers, selectively include transactions that maximize their revenue while ensuring successful block proposals.
This analysis highlighted the varied strategies employed by different builders in the current PBS framework, revealing significant differences in how they time their bids. This information asymmetry can lead to mispricing of MEV transactions, potentially reducing the overall value of blocks for node operators.
The presence of preconfirmations forces searchers to engage in more sophisticated bidding strategies. They must carefully balance the risk of being outbid by competitors against the potential for an early auction termination, which could prevent their transactions from being included. This dynamic is akin to a modified prisoner’s dilemma, where searchers must decide between bidding aggressively early or waiting for a more opportune moment, knowing that their decisions impact the overall auction outcome. Overall, this may push for a new type of timing games, where now searchers will compete more aggressively in the first part of the preconfirmation interval.
Complex implementation of preconfirmations provide NOs with a powerful tool to capture on-chain MEV directly. By preconfirming their transactions, NOs can ensure the inclusion of high-value arbitrage and liquidation opportunities, significantly boosting their MEV revenue. Our calculations indicate that a NO with a 1% stake penetration could see a 25.17% increase in annual MEV revenue through strategic use of preconfirmations. This increase is substantial compared to the ~10% extra MEV derived from current timing games.
Despite the potential benefits, the implementation of preconfirmations must be carefully managed to avoid centralization risks. A decentralized approach, where proposers themselves manage preconfirmations, is preferable to a gateway architecture that could lead to undue centralization and higher switching costs.
Appendix A
Deriving the trade probability
To see where Eq. (2) comes from, let’s model the price difference between CEX and DEX as a Markovian jump-diffusion process. This allows us to derive the expression for the probability that stat-arbitrageurs can execute a profitable trade, i.e. that the price difference is higher than the fees needed to execute the trade.
If we assume that DEX and CEX prices follows a Brownian motion, since the difference between two Brownian motion is still a Brownian motion, we can model the price difference as a Brownian motion with volatility \sigma
where \mu_M represents the drift of motion. In the presence of discrete time arrival for trades (i.e. jumps) modelled as a Poisson process with rate \lambda, we get
where j(M_{t-1}) dN(t) is the contribution from jumps (depending only on immediately previous state j(M_{t-1}), that’s where the Markovian approximation comes in). The density p(x,t) of the process M(t) is governed by Fokker-Planck equation
where the Dirac \delta determine the dimension of the jump (we are assuming constant jumps) and \lambda is the mean dimension of jumps in the price difference. In the absence of drift, the equation of the process is
To find the stationary distribution (i.e. p(x)), we can consider the case with \partial_tp(x,t)=0, such that Fokker-Planck equation becomes
Now, if we consider the Taylor expansion of p(x) for small j we obtain
which gives
If we now observe that for
we can neglect second order terms in j. For the next part of the paper we’ll use
which means the dimension of the jump between trades is given by the volatility of price difference times the square root of half the time interval between trades. Under these assumptions our Fokker-Planck equation becomes
This is a second order differential equation, with solution of the form
where r_1 and r_2 are the solution of
It follows that
Since p(x) is a density, it has to be normalized and not diverging for x\to\pm\infty. This means that the solution has to be
where
The nature of p_2(x) is that it is null at infinity. Now, if we impose continuity of p(x) at boundaries, we have
It follows that, by imposing the symmetry condition and the fact that p(x) is a density we get
where we introduced the parameter \xi=\frac{\sqrt{2\lambda}\gamma}{\sigma}, characterizing the behaviour of the price difference process. By solving for A, it follows that
Now, we are interested in computing the probability of the trade area. This has as density
and since
is the density of an exponential distribution and that is the only part dependent from x, we have that the invariant for the trade region probability is
that is the result used in Eq. (2). Note that this result is consistent with what presented in Milionis et al, even if the derivation is different.