Here is something I’ve been working on for some time already. Not perfect, but as privacy-preserving multisig as possible. Would love to hear your feedback!
Please do check out my other, but related research papers: Confidential Wrapped Ethereum and ZEX: Confidential Peer-to-Peer DEX.
Also, take a look at the magnificent Ethereum Privacy Roadmap.
Abstract
The paper proposes a practical approach to implement a Zero Knowledge (ZK) EVM-based multi-signature wallet to preserve the privacy and confidentiality of collective decisions. The approach combines three core features: Merkle tree membership proofs for anonymity, aggregated ECC ElGamal encryption for participants’ votes confidentiality with bias-free decision making, and Distributed Key Generation (DKG) for non-interactiveness in the keys deduction and elimination of centralized, trusted entities.
The proposed solution consists of Solidity smart contracts and ZK circuits. The former plays the role of an accounts factory and the actual accounts that users interact with to create multisigs and execute collective proposals. The latter is responsible for checking users’ belonging to the multisig sets and verifying their decisions on whether to execute a proposal or not, without revealing intermediate results.
The downside of the proposed approach is that all multisig participants must vote on the proposal to calculate its outcome.
1. Introduction
The transparency of public blockchains offers a multitude of advantages, including enhanced traceability of actions, execution verifiability, and openness of data that is available to everyone. However, it poses unique challenges in multiparty decision-making, particularly in preserving privacy and preventing voting bias — fundamental aspects of a secure and impartial multisig wallet.
The goal is to create a simple, permissionless multisig that doesn’t disclose anything about its members and provides multisig voters with the assurance that their ballots are secret and their choices are not influenced by how early participants vote.
The multisig would allow users to be included/excluded from the members list, the configuration of the “signature threshold”, and execution of collectively approved transactions, with (almost) zero compromises in privacy. Along with that, users will be able to vote for or against the proposals without knowing the individual votes or the result until all the users from the membership list have cast their ballots.
Of course, the important limitation is that the last voting participant will be able to decrypt and see the ongoing proposal direction prior to casting and disclosing their vote.
2. Specification
2.1. Application flow
Before proceeding with the technical deep-dive, it is essential to see the high-level picture and understand the basic application flow. The flows for a multisig wallet creation, proposal creation, and generic multisig transaction execution with proposal voting are provided.
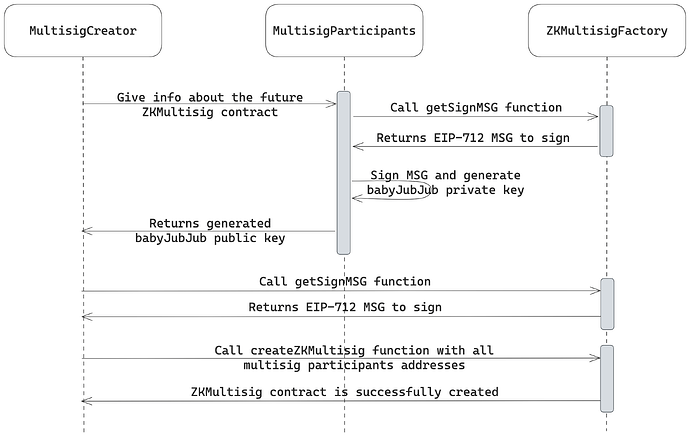
2.1.1. Multisig creation
The cornerstone of the application is the multisig wallet. Upon interacting with the application, users create multisigs with the list of permitted voters for their business logic.
The multisig creation flow is depicted in the following diagram:
-
The creation flow starts with the user (wallet creator) gathering the public keys of the voters to be added to the permitted list. Since the multisig utilizes ZK to maintain privacy, all the users have to create a special babyJubJub key pair that will be used as their unique identifier before using the application.
To create these keys, users sign an EIP-712 structured message with their Ethereum (ECDSA) private key and hash the obtained signature. The resulting hash is the babyJubJub private key.
Users may choose between signing the unique messages to get unique public keys for every multisig they are willing to participate in (increases privacy) or using the “default” message to stick to a single public key to be utilized across the platform (possibly better UX).
-
Having acquired all the necessary babyJubJub public keys, the wallet creator invokes the wallet creation function on the
ZKMultisigFactorysmart contract, providing all the public keys to be added to the permitted list. Under the hood, the multisig stores the participants in a Sparse Merkle Tree (SMT) data structure, enabling ZK-provable membership proofs and cheap list maintenance. -
After the multisig wallet is deployed, its members can create proposals and vote on them by generating ZK proofs of membership and applying EdDSA blinders for decision non-reusability.
With the described approach, we can achieve full privacy for the users by abstracting their real “wallet address” with a babyJubJub one through a deterministic key derivation function (KDF) and decrease the probability of determining the decision-making address from 1 to 1/N, where N is the number of multisig members.
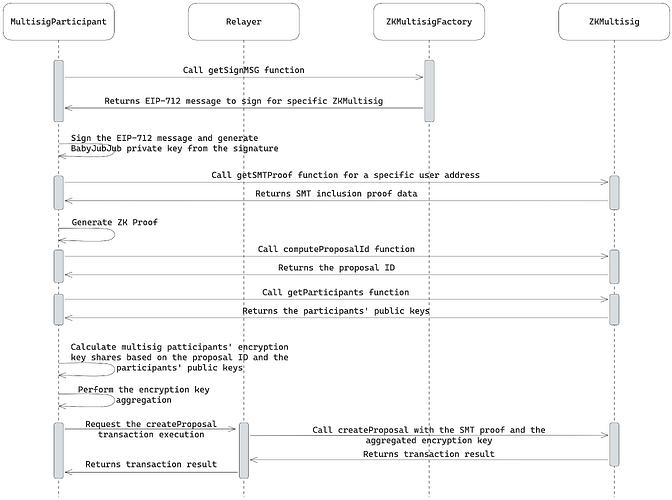
2.1.2 Proposal creation
The proposal creation flow is depicted in the diagram below:
-
The proposal creator (a user from the multisig permitted list) logs in to the application by deterministically recovering the babyJubJub key pair from the “multisig wallet creation” step.
The KDF algorithm remains the same. The EIP-712 structured message is obtained from the
ZKMultisigFactory, then signed, and the signature is hashed to calculate the babyJubJub private key. -
The user generates a ZK proof that permissionlessly verifies their membership in the multisig via an SMT inclusion proof.
-
The proposal creator computes the ID of the proposal to be used in the generation of a one-time aggregated encryption key.
-
The creator non-interactively calculates the encryption key share of every multisig participant using KDF based on the proposal ID and the participants’ babyJubJub public keys.
-
After calculating all the encryption key shares, the creator aggregates them into the final encryption key.
-
The proposal creator invokes the
createProposalfunction via the relayer, providing the SMT inclusion proof and the aggregated key to be further used for votes encryption.
After the proposal is created, multisig participants can start casting their votes.
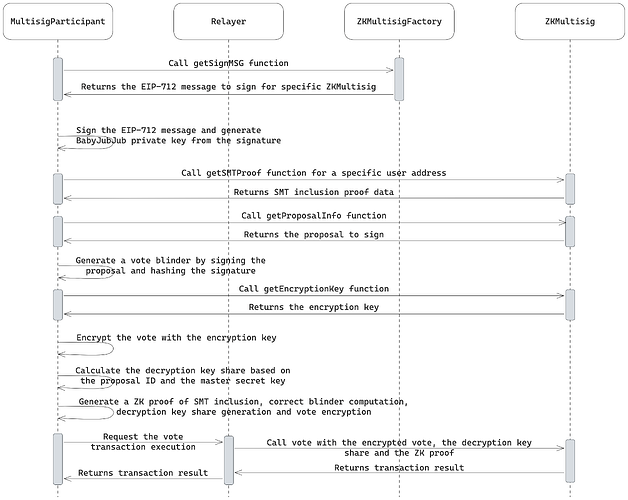
2.1.3. Voting on the proposal
The voting on the proposal flow is depicted in the following diagram:
-
The SMT inclusion (Merkle) proof is fetched from the contract to indicate that the user is a member of the multisig.
-
The user signs (with their babyJubJub private key) the proposal they are voting on to generate a blinder by hashing the obtained EdDSA signature. It is used to verify that they have not previously voted for the same proposal.
-
The user fetches the encryption key of the proposal.
-
The received ephemeral encryption key is used to encrypt their vote.
-
Based on the proposal ID, the user calculates the decryption key share using their babyJubJub private key and KDF.
-
After calculating all the needed data, the multisig participant invokes the
votefunction via the relayer, providing the encrypted vote, decryption key share, and the ZK proof. -
The smart contract adds the provided decryption key share to the aggregatable final decryption key and sets the vote as successfully cast.
2.1.4 Vote Revelation and Proposal Execution
Only when the last participant has voted is the decryption key complete and can be used to reveal the voting outcome. This is done by calling the reveal function. It decrypts the aggregated votes and changes the proposal status according to the voting result. If the number of “for” votes exceeds the “signature threshold”, the proposal is set to be “accepted” and can be executed, “rejected” otherwise.
The diagram below illustrates the votes revelation process, encapsulating the decryption and execution logic into the single function revealAndExecute.
2.2. Encryption Math
This section provides the mathematical foundation of the votes encryption logic used in the protocol.
2.2.1. Elliptic Curve Arithmetic Operations
In the context of this document, certain operations are performed on elliptic curves and involve specific mathematical operations distinct from conventional arithmetic:
- Point addition P + Q, where P and Q are points on the elliptic curve, is performed according to the defined group operation logic.
- Scalar multiplication k \times P, where k is a scalar and P is a point on the elliptic curve, involves adding the point P to itself k times.
- Point subtraction P - Q, where P and Q are points on the elliptic curve, and is identical to P + (-Q), where -Q is the inverse of point Q.
2.2.2. KDF for Encryption Keys
The protocol utilizes the stealth key schema CoM17 [1] as the deterministic KDF. Such a schema enables the generation of unique key shares to encrypt and decrypt votes for each proposal out of the master keys.
The master key pair must satisfy the following:
pk = sk \times G,
where pk — master public key,
sk — master secret key,
G — base point on the elliptic curve.
The babyJubJub key pair generated during the wallet creation is used as the master key pair from which the ElGamal encryption and decryption keys are derived. The key derivation procedure is described below.
First, the challenge is computed based on the proposal ID. Note that the multisig intentionally omits the incremental enumeration of proposals to prevent ZKPs replay and frontrunning attacks. This is achieved by asking the proposal creator to sign the challenge of the proposal they are creating. The proposal ID and the challenge are deterministically calculated as follows:
proposalId = keccak256(abi.encode(target, value, data, salt));
challenge = poseidon(uint248(keccak256(abi.encode(chainid, zkMultisigAddress, proposalId))));
Let r be equal to the challenge and R be the challenge point:
R = r \times G
The encryption key share is derived as follows:
P_i = poseidon(r \times pk_i) \times G + pk_i
Correspondingly, the decryption key share is derived as follows:
x_i = (poseidon(sk_i \times R) + sk_i) \mod n
where n — order of the elliptic curve.
The consistency of the key derivation scheme can be proved by:
P_i = x_i \times G = (poseidon(sk_i \times R) + sk_i) \times G =
= poseidon(sk_i \cdot r \times G) \times G + sk_i \times G = poseidon(r \times pk_i) \times G + pk_i
2.2.3. ECC ElGamal Encryption Scheme
The protocol utilizes the Elliptic Curve Cryptography (ECC) modification of the ElGamal encryption scheme [2] to encrypt and, hereinafter, decrypt the multisig votes.
The aggregated encryption key P is a point on the elliptic curve computed by summing all encryption key shares:
P = \sum_{i=1}^N P_i,
where N — number of the multisig participants,
P_i — encryption key share (elliptic curve point).
The participant’s vote is mapped to a point M on the elliptic curve. The generator point G is used as the “for” vote, and the point at infinity as the “against”. A random value k satisfying 0<k<n is chosen. Afterward, the ciphertext (C_1, C_2) is computed:
C_1 = k \times G
C_2 = M + k \times P
To decrypt the vote, first compute the aggregated decryption key share:
x = \sum_{i=1}^N x_i \mod n,
where n — order of the elliptic curve,
x_i — decryption key share (scalar).
Then use the computed aggregated decryption key x to recover the message point M:
M = C_2 - x \times C_1
The consistency of the key aggregation within the ECC ElGamal scheme can be proved as follows:
P = \sum_{i=1}^N P_i = \sum_{i=1}^N x_i \times G
D = x \times C_1 = \sum_{i=1}^N x_i \times C_1 = \sum_{i=1}^N x_i \cdot k \times G = k \times (\sum_{i=1}^N x_i \times G) = k \times P
M = C_2 - D = M + k \times P - k \times P
2.2.4. Homomorphic aggregation of votes
Using point G and point at infinity as votes makes it possible to form the cumulative voting result homomorphically, summing up the encrypted votes during each vote cast:
SC_1 = \sum_{i=1}^N C_{1_i}
SC_2 = \sum_{i=1}^N C_{2_i}
Decrypt the sum to get the aggregated result T:
T = \sum_{i=1}^N M_i = SC_2 - x \times SC_1
The decrypted total T is equal to v \times G, where v is the total number of voters who voted “for” the proposal.
To reveal the votes, a multisig participant must loop through the possible scalar values v_i off-chain, where 0 \leq v_i \leq N, to find the value that satisfies the equation:
v_i \times G = T
Then they submit this value to the smart contract, where the above equation is checked.
- If v < signaturesQuorum, not enough participants have voted “for” the proposal and its status is set to “rejected”;
- If v \geq signaturesQuorum, enough participants have voted “for” the proposal and its status is set to “accepted”.
2.2.5. Encryption Key On-Chain Calculation
When the proposal gets created, it is essential to check that the aggregated encryption key was computed correctly from the individual public keys and the challenge.
As this value is publicly computable, it can be evaluated on the smart contract by looping through the participants’ master public keys and deriving their encryption shares. However, this approach is suboptimal and can be improved by introducing a cumulative public key, which represents the sum of all participants’ master public keys. This key is stored on the smart contract and has to be updated whenever the membership list is updated.
Instead of calculating the encryption key share for each participant individually:
P_i = poseidon(r \times pk_i) \times G + pk_i
It is enough to calculate only the hash part and add it to the sum of previous hashes, reducing the number of operations inside the loop:
sumHash = sumHash + poseidon(r \times pk_i)
Then the aggregated encryption key can be computed as follows:
aggKey = sumHash \times G + cumulativePk
2.3. Functionality
In this section, the technical description of smart contracts and circuits is provided. The section outlines the required functionality to be supported by the components to implement the workable prototype.
2.3.1. ZKMultisigFactory
There are two contracts in the application: ZKMultisigFactory and ZKMultisig. The factory is used to create multisig wallets and generate EIP-712 messages that are required for the key derivation procedure. ZKMultisig is the implementation of the wallet itself.
The ZKMultisigFactory interface is defined as follows:
interface IZKMultisigFactory {
event ZKMultisigCreated(
address indexed zkMultisigAddress,
uint256[2][] initialParticipants,
uint256 initialQuorumPercentage
);
function createZKMultisig(
uint256[2][] calldata participants,
uint256 quorumPercentage,
uint256 salt
) external returns (address);
function computeZKMultisigAddress(
address deployer,
uint256 salt
) external view returns (address);
function getKDFMSGToSign(address zkMultisigAddress) external view
returns (bytes32);
function getDefaultKDFMSGToSign() external view returns (bytes32);
function isZKMultisig(address multisigAddress) external view returns(bool);
}
ZKMultisigFactory does not deploy the wallets directly, rather, the ERC-1967 proxies are deployed. Moreover, the create2 approach is taken to provide determinism to the wallets addresses to establish the KDF messages upfront.
The salt in the create2 is defined as follows:
realSalt = keccak256(abi.encode(msg.sender, salt));
Users may decide which KDF message to sign:
- The unique message per wallet (increases privacy assumptions);
- The default one (possibly better UX).
The structure of the returned messages can be found in section 2.3.6.
2.3.2 ZKMultisig
ZKMultisig is a contract that implements the multisig functionality. The implementation includes the management of multisig participants, quorum settings, proposal creation, voting, and their execution. The ZKMultisig interface is defined as follows:
import "@solarity/solidity-lib/libs/data-structures/SparseMerkleTree.sol";
interface IZKMultisig {
enum ProposalStatus {
NONE,
VOTING,
ACCEPTED,
REJECTED,
EXPIRED,
EXECUTED
}
struct ZKParams {
uint256[2] a;
uint256[2][2] b;
uint256[2] c;
uint256[] inputs;
}
struct ProposalContent {
address target;
uint256 value;
bytes data;
}
struct ProposalInfoView {
ProposalContent content;
ProposalStatus status;
uint256 proposalEndTime;
uint256 votesCount;
uint256 requiredQuorum;
}
event ProposalCreated(uint256 indexed proposalId, ProposalContent content);
event ProposalVoted(uint256 indexed proposalId, uint256 voterBlinder);
event ProposalExecuted(uint256 indexed proposalId);
function addParticipants(
uint256[2][] calldata participantsToAdd
) external;
function removeParticipants(
uint256[2][] calldata participantsToRemove
) external;
function updateQuorumPercentage(uint256 newQuorumPercentage) external;
function create(
ProposalContent calldata content,
uint256 duration,
uint256 salt,
ZKParams calldata proofData
) external returns (uint256);
function vote(
uint256 proposalId,
bytes calldata encryptedVote,
uint256 decryptionKeyShare,
ZKParams calldata proofData
) external;
function reveal(uint256 proposalId, uint256 approvalVoteCount) external;
function execute(uint256 proposalId) external;
function revealAndExecute(
uint256 proposalId,
uint256 approvalVoteCount
) external;
function getPerticipantsSMTRoot() external view returns (bytes32);
function getParticipantsSMTProof(bytes32 publicKeyHash)
external view returns (SparseMerkleTree.Proof memory);
function getParticipantsCount() external view returns (uint256);
function getParticipants() external view returns (uint256[2][] memory);
function getProposalsCount() external view returns (uint256);
function getProposalsIds(uint256 offset, uint256 limit)
external view returns (uint256[] memory);
function getQuorumPercentage() external view returns (uint256);
function getEncryptionKey(uint256 proposalId) external view
returns (uint256[2] memory);
function getProposalInfo(uint256 proposalId) external view
returns (ProposalInfoView memory);
function getProposalStatus(uint256 proposalId) external view
returns (ProposalStatus);
function getProposalChallenge(uint256 proposalId)
external view returns (uint256);
function computeProposalId(
ProposalContent calldata content,
uint256 salt
) external view returns (uint256);
function isBlinderVoted(
uint256 proposalId,
uint256 blinderToCheck
) external view returns (bool);
}
It is crucial to verify ElGamal encryption key aggregation inside the createProposal function for the given proposal. The smart contract has to loop through the active members’ master public keys, deriving their encryption key shares, which are subsequently aggregated into the encryption key (see section 2.2.5).
2.3.3 Proposal creation circuit
Every parameter in this paper is provided with the intent to be provable and compatible with zero-knowledge circuits. The list of circuit signals for the proposal creation proof is the following:
Public signals:
- SMT root (input);
- Proposal ID (input).
Private signals:
- Master secret key;
- Master public key [optional];
- SMT inclusion proof.
Utilizing these signals, the circuit must have the following constraints:
- The provided master secret key is indeed the secret key of the provided master public key.
- The master public key belongs to the SMT, anchoring to the SMT root.
2.3.4. Proposal voting circuit
The list of circuit signals for the proposal voting proof is the following:
Public signals:
- User blinder (output);
- Decryption key share (output);
- Encryption point C_1 (output);
- Encryption point C_2 (output);
- Aggregated encryption key (input);
- Proposal challenge (input);
- SMT root (input).
Private signals:
- Master secret key;
- Master public key [optional];
- EdDSA master signature of the challenge;
- The actual vote: point G or inf;
- The random encryption value k;
- SMT inclusion proof.
Utilizing these signals, the circuit must have the following constraints:
- The provided master secret key is indeed the secret key of the provided master public key.
- The master public key belongs to the SMT, anchoring to the SMT root.
- The EdDSA master signature of the challenge verifies against the master public key.
- The poseidon hash of the signature is equal to the user blinder.
- The decryption key share is calculated correctly given the master secret key and the proposal challenge (see section 2.2.2).
- The provided vote is either equal to G or inf.
- The encryption has been performed correctly given the aggregated encryption key, the random encryption value k, and the vote (see section 2.2.3).
2.3.5. KDF
Key Derivation Function (KDF) is such a function that deterministically creates a babyJubJub private key from some input. In our case, the input is the Ethereum ECDSA signature of the EIP-712 formatted message.
The KDF is defined as follows:
message = getKDFMSGToSign() or getDefaultKDFMSGToSign();
signature = eth_signTypedData_v4(message);
privateKey = keccak256(keccak256(signature));
Note that it is crucial never to reveal the signature as the private key derives from it directly.
2.3.6. KD EIP-712 message
To create a key derivation EIP-712 message, a KDF message typehash is used that includes the ZKMultisig address of the contract. This is sufficient as the network and the contract information are included in the standard EIP-712 domain structure.
bytes32 KDF_MSG_TYPEHASH = keccak256("KDF(address zkMultisigAddr)");
bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, zkMultisigAddress));
The getKDFMSGToSign() and getDefaultKDFMSGToSign() functions create an EIP-712 message as described above. The getDefaultKDFMSGToSign() function uses a zero address for the construction of the default message.
2.3.7. Relayers
Since the above approach is completely independent of the EVM addresses from which transactions are sent, users can utilize different relayers to preserve anonymity. Protocol-friendly relayers such as GSN can be used, however, this requires additional integration logic on the front end.
3. Rationale
The ECC modification of the ElGamal encryption scheme [2] was selected for its compatibility with key derivation functions (KDFs) and key aggregation. ElGamal’s non-deterministic nature, introduced by the random value k, guarantees that each encryption operation produces a unique ciphertext, enhancing security.
To mitigate centralization risks associated with traditional decryption key management, like in the Shamir Secret Sharing (SSS) scheme, where the existence of a decryption key before secret sharing is required, the Distributed Key Generation (DKG) approach was taken. It provides the mechanism to generate the decryption key in a decentralized way by every participant, so that no single party possesses the complete key before revelation.
Most DKG protocols remove the need for a trusted party by employing Verifiable Secret Sharing (VSS), which mandates participant interaction to verify share validity. This process is replaced by verifying ZK proofs of decryption key shares on demand when casting the vote.
Although DKG eliminates the need for key share exchange between parties, it still requires publishing encryption key shares during proposal creation. Using a deterministic KDF, participants can avoid interactive processes, enabling the proposal creator to aggregate the final encryption key asynchronously and independently.
4. Security Considerations and Limitations
There are several security risks and limitations inherent to the protocol that need to be considered:
-
Trusted setup. If Groth16 is used as a zk-SNARK proving system, a per-circuit trusted setup is required and must be properly carried out.
-
Private key/signature leaks. It is essential to keep the key derivation ECDSA signature private. The babyJubJub key pair is derived directly from it, so leaking the signature would render the multisigs (in which the user is in) vulnerable to phishing / spamming attacks.
-
Proposal frontrunning. Even though the proposal challenge is derived deterministically from the proposal contents, it is still possible to frontrun the proposal creation with an identical proposal. This does not directly impact security, yet it should be noted.
-
Participant removal deadlock. If a participant to be removed does not vote (which is natural to them), the removal proposal expires, and the participant remains a multisig member. A possible solution may be to vote openly on such proposals.
-
Modification of participant list. It is challenging to add or remove participants from the multisig whenever there are active (ongoing) proposals. Doing this may cause inconsistency in the keys used within the encryption scheme. A possible solution may be to track such proposals and allow their creation only when nothing else is in progress.
-
Last-voter advantage. Since the decryption of votes is possible once all decryption key shares are known, the last participant can reconstruct prior votes before casting their own.
-
Scalability. Votes revelation and proposal results calculation complexity scales linearly with the number of participants.
References
[1] Nicolas T. Courtois and Rebekah Mercer. Stealth Address and Key Management Techniques in
Blockchain Systems. 2017. url: https://www.scitepress.org/papers/2017/62700/62700.pdf.
[2] Neal Koblitz. Elliptic Curve Cryptosystems. 1987. url: https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf.