Slashing penalty analysis; EIP-7251
by mike & barnabé
august 30, 2023
\cdot
tl;dr;
The primary concern around the proposal to increase the MAXIMUM_EFFECTIVE_BALANCE (EIP-7251) is the increased slashing risk taken on by validators with large effective balances. This doc explores the 4 types of penalties incurred by a slashed validator and how these penalties scale with effective balance.
We propose
(i) the initial penalty is fixed to a constant amount or modified to scale sublinearly, and
(ii) the correlation penalty is modified to scale quadratically rather than linearly.
Conversely, we suggest leaving the attestation and inactivity leak penalties unchanged.
The code used to generate the figures in this article is available here. Thanks to Ben Edgington for his ETH2 Book and Vitalik for his Annotated spec – both of which serve as excellent references.
\cdot
Motivation
Validator rewards are computed to scale with validator balances, such that an entity with half the stake receives half the rewards. This fairness principle is important to facilitate economic decentralization and avoid economies of scale. However, validator penalties need not exhibit the same dynamics. Penalties are computed today based on slashing the entire balance of all validators participating in an attack involving 1/3+ of the stake and preventing the strategic use of intentional slashing to avoid incurring inactivity penalties. Slashed amounts function as a credible threat, and while it is important to levy high penalties for critical attacks, we also don’t want to deter socially beneficial participation in protocol changes (e.g., validator balance consolidation) due to unnecessarily high risks.
\cdot
Contents
\cdot
Related work
| title | description |
|---|---|
| proposal | initial ethresear.ch post |
| diff pr | diff-view PR showing the proposed spec change |
| security considerations doc | analysis of the security implications of this change |
| eip pr | EIP-7251 open PR |
| faq doc | FAQ on the proposal |
| responses to questions | Q&A based on questions from LIDO |
\cdot
Thanks
Many thanks to Terence, Vitalik, Mikhail, Lion, stokes and Izzy for relevant discussions.
1. Initial slashing penalty
When a validator is slashed, slash_validator applies an initial penalty proportional to the effective balance of the validator.
def slash_validator(state: BeaconState, slashed_index: ValidatorIndex, ...) -> None:
...
slashing_penalty = validator.effective_balance // MIN_SLASHING_PENALTY_QUOTIENT_BELLATRIX
decrease_balance(state, slashed_index, slashing_penalty)
With MIN_SLASHING_PENALTY_QUOTIENT_BELLATRIX=32, validators with an effective balance of 32 ETH (the current MAX_EFFECTIVE_BALANCE) are slashed exactly 1 ETH. Without changing this function, the slashing penalty of a validator with an effective balance of 2048 ETH (the proposed new MAX_EFFECTIVE_BALANCE), would be 64 ETH. The initial slashing penalty scales linearly with the effective balance of the validator, making it inherently more risky to run validators with larger effective balances. We could simply make this initial penalty constant.
def slash_validator(state: BeaconState, slashed_index: ValidatorIndex, ...) -> None:
...
- slashing_penalty = validator.effective_balance // MIN_SLASHING_PENALTY_QUOTIENT_BELLATRIX
+ slashing_penalty = MIN_SLASHING_PENALTY
decrease_balance(state, slashed_index, slashing_penalty)
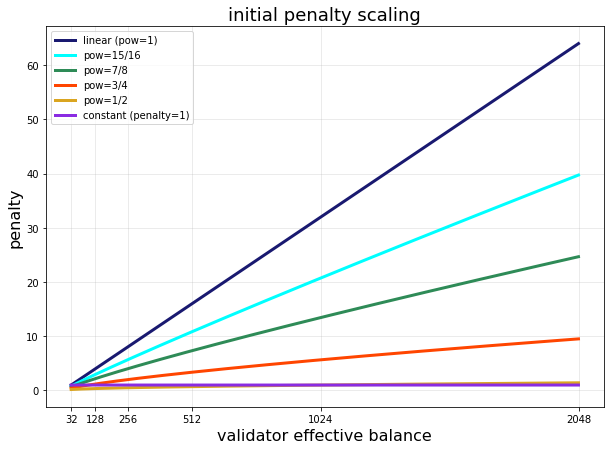
Here, with MIN_SLASHING_PENALTY=1, we ensure that everyone is slashed exactly 1 ETH for the initial penalty. If we decide that a constant penalty is insufficient, there are various sublinear functions we could use to make the initial penalty less punitive but still monotone increasing in the effective balance. Let EB denote the effective balance of a validator. For the range EB \in [32, 2048], consider the family of polynomials
The figure below shows a few examples for values of \text{pow} \leq 1.
On inspection, if we were to choose from this family of non-constant functions, \text{pow}=3/4 or \text{pow}=7/8 seem to provide a reasonable compromise of still punishing larger validators while reducing their absolute risk significantly.
2. Correlation penalty
The correlation penalty is applied at the halfway point of the validator being withdrawable (normally around 4096 epochs, about 18 days, after the slashing). The process_slashings function applies this penalty.
def process_slashings(state: BeaconState) -> None:
epoch = get_current_epoch(state)
total_balance = get_total_active_balance(state)
adjusted_total_slashing_balance = min(
sum(state.slashings) * PROPORTIONAL_SLASHING_MULTIPLIER_BELLATRIX, # [Modified in Bellatrix]
total_balance
)
for index, validator in enumerate(state.validators):
if validator.slashed and epoch + EPOCHS_PER_SLASHINGS_VECTOR // 2 == validator.withdrawable_epoch:
increment = EFFECTIVE_BALANCE_INCREMENT # Factored out from penalty numerator to avoid uint64 overflow
penalty_numerator = validator.effective_balance // increment * adjusted_total_slashing_balance
penalty = penalty_numerator // total_balance * increment
decrease_balance(state, ValidatorIndex(index), penalty)
Let EB denote the “effective balance” of the validator, SB denote the “slashable balance” (the correlated ETH that is slashable), and TB denote the “total balance” of the beacon chain, then
If 1/3 of the total stake is slashable, the penalty equals the effective balance of the validator;
On the other hand, because the penalty is calculated with integer division, we have
This implies that for isolated slashing events, the correlation penalty is zero. Putting some numbers to this, we currently have 24 million ETH staked. This implies that even a 2048 ETH validator that is slashed in isolation would not have any correlation penalty because
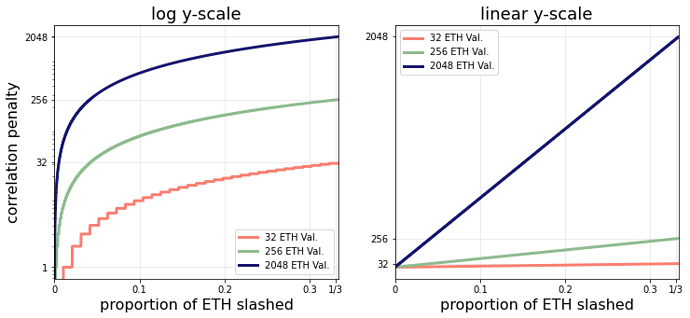
The figure below shows the correlation penalty as a function of the proportion of slashable ETH for different validator sizes.
The rate at which the correlation penalty increases for large validators is higher because the validator effective balance is the coefficient of the linear function on the ratio of SB and TB. Notice that these linear functions must have the property that when the proportion of ETH slashed is 1/3, the penalty is the entire validator balance. We could leave this as is, but if we wanted to encourage more validator consolidation, we could reduce the risk of larger correlation penalties for validators with higher effective balances. Consider the following new correlation penalty:
Notice that this still has the property
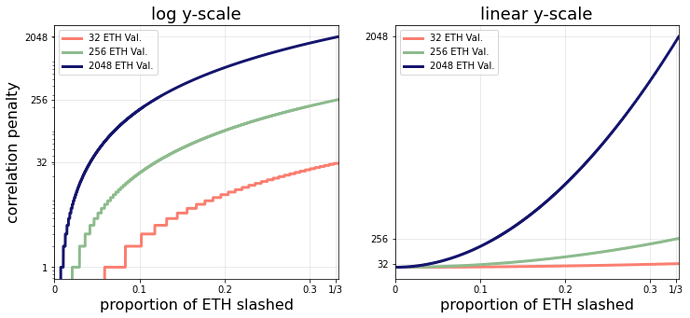
The penalty scales quadratically rather than linearly. The plot below demonstrates this.
Now the validator effective balance is the coefficient of the quadratic. The important point is that at 1/3-slashable ETH, the penalty is the full effective balance. Under this scheme, the consolidated validator faces less risk than in the linearly scaling penalty of today. The figure below demonstrates this point.
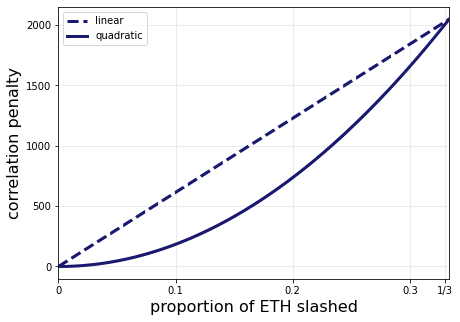
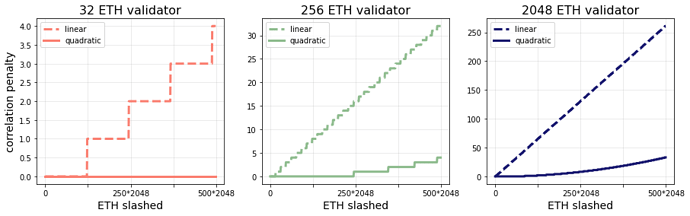
At every proportion of ETH slashed below 1/3, the quadratic penalty (solid line) results in less ETH lost than the linear penalty (the dashed line). We can also take a zoomed-in look at the penalties when smaller amounts of ETH are slashed. The figure below shows the penalties for different validator sizes under both the linear and quadratic schemes for up to 500 * 2048 = 1,024,000 ETH slashed in the correlation period.
This figure shows that all validator sizes have less correlation risk under the quadratic scaling. The diff below shows the proposed modified process_slashings function.
def process_slashings(state: BeaconState) -> None:
...
+ penalty_numerator = validator.effective_balance**2 // increment * adjusted_total_slashing_balance
+ penalty_numerator *= PROPORTIONAL_SLASHING_MULTIPLIER_BELLATRIX
+ penalty = penalty_numerator // total_balance**2 * increment
decrease_balance(state, ValidatorIndex(index), penalty)
3. Attestation penalty
When a validator is slashed, their attestations are no longer considered valid. They are penalized as if they went offline for the 8192 epochs until they become withdrawable. Attestations contain “source”, “target”, and “head” votes. In get_flag_index_deltas the penalties are applied only for the “source” and “target” votes. The relative weights of these votes are specified here. We care about TIMELY_SOURCE_WEIGHT=14, TIMELY_TARGET_WEIGHT=26, and WEIGHT_DENOMINATOR=64. For each of the EPOCHS_PER_SLASHINGS_VECTOR=8192 epochs, the slashed validator will be penalized
Here the “base reward” is defined in get_base_reward as
With TB at 24 million ETH, we have \lfloor\sqrt{TB} \rfloor = 4898, which gives a base reward of 413 GWEI. For a 32 ETH validator, we have
For a full 2048 ETH validator, the attestation penalty just scales linearly with the effective balance, so we have
We don’t think this penalty needs to change because it is still relatively small. However, we could consider reducing the attestation penalties by modifying the number of epochs that we consider the validator “offline”. These penalties ensure that it is never worth it to self-slash intentionally to avoid inactivity penalties. Thus as long as the penalty is larger than what an unslashed, exiting, offline validator would pay, we don’t change the security model.
4. Inactivity leak penalty
If the chain is in an “inactivity leak” state, where we have not finalized for MIN_EPOCHS_TO_INACTIVITY_PENALTY=4 epochs (see is_in_inactivity_leak), there is an additional set of penalties levied against the slashed validator. Fully online validators should earn exactly 0 rewards, while any offline validators will start to leak some of their stake. This enables the chain to reset by increasing the relative weight of online validators until it can finalize again. Since a slashed validator appears “offline” to the chain, the inactivity leak can significantly punish them for not fulfilling their duties.
Inactivity leak penalties are calculated in get_inactivity_penalty_deltas, which is included below.
def get_inactivity_penalty_deltas(state: BeaconState) -> Tuple[Sequence[Gwei], Sequence[Gwei]]:
"""
Return the inactivity penalty deltas by considering timely target participation flags and inactivity scores.
"""
rewards = [Gwei(0) for _ in range(len(state.validators))]
penalties = [Gwei(0) for _ in range(len(state.validators))]
previous_epoch = get_previous_epoch(state)
matching_target_indices = get_unslashed_participating_indices(state, TIMELY_TARGET_FLAG_INDEX, previous_epoch)
for index in get_eligible_validator_indices(state):
if index not in matching_target_indices:
penalty_numerator = state.validators[index].effective_balance * state.inactivity_scores[index]
# [Modified in Bellatrix]
penalty_denominator = INACTIVITY_SCORE_BIAS * INACTIVITY_PENALTY_QUOTIENT_BELLATRIX
penalties[index] += Gwei(penalty_numerator // penalty_denominator)
return rewards, penalties
A few notable constants:
The penalty_numerator is the product of the effective balance of the validator and their “inactivity score”. See Vitalik’s annotated spec for more details about the inactivity scoring. The inactivity score of each validator is updated in process_inactivity_updates.
def process_inactivity_updates(state: BeaconState) -> None:
# Skip the genesis epoch as score updates are based on the previous epoch participation
if get_current_epoch(state) == GENESIS_EPOCH:
return
for index in get_eligible_validator_indices(state):
# Increase the inactivity score of inactive validators
if index in get_unslashed_participating_indices(state, TIMELY_TARGET_FLAG_INDEX, get_previous_epoch(state)):
state.inactivity_scores[index] -= min(1, state.inactivity_scores[index])
else:
state.inactivity_scores[index] += config.INACTIVITY_SCORE_BIAS
# Decrease the inactivity score of all eligible validators during a leak-free epoch
if not is_in_inactivity_leak(state):
state.inactivity_scores[index] -= min(config.INACTIVITY_SCORE_RECOVERY_RATE, state.inactivity_scores[index])
During an inactivity leak period, a slashed validator will have their inactivity score incremented by 4 points every epoch. Each point is a pseudo “1 ETH” of additional effective balance to increase the punishment against offline validators. The table below shows varying-length inactivity leak penalties for differing validator sizes. The penalties scale linearly with the validator’s effective balance.
| validator size | 16 epoch leak | 128 epoch leak | 1024 epoch leak |
|---|---|---|---|
| 32 ETH | 0.000259 ETH | 0.0157 ETH | 1.00 ETH |
| 256 ETH | 0.00208 ETH | 0.126 ETH | 8.01 ETH |
| 2048 ETH | 0.0166 ETH | 1.01 ETH | 64.1 ETH |
These penalties feel pretty well contained for large validators, so we propose not modifying them because the leak is already relatively gradual.