Many thanks to Vitalik Buterin, Alexander Herrmann, Philogy, William X, Thomas Thiery, and Julian Ma for feedback and discussions.
Solo validators are vital to Ethereum’s security, decentralization, and censorship resistance. They operate independent nodes distributed around the world that cannot be easily coerced. However, they face key challenges:
-
High entry barriers: The 32 ETH staking requirement is prohibitively high for many potential participants.
-
Opportunity costs: Significantly more capital is locked up than what’s likely to be lost in cases of validator misbehavior.
-
Limited liquidity: Solo validators can’t easily borrow against their stake and obtain leverage while still operating the validator.
To address these issues, we propose SOLO—a protocol that enables a permissionless liquid staking token (LST) minted against the portion of a validator’s stake that’s unlikely to be lost, even in cases of penalties and slashing. Following the Pectra update, this could be as much as 96.1% of the stake, barring significant concurrent mass slashing events and long inactivity leaks. This would reduce entry costs for solo validators by a factor of 25.6, to just 1.25 ETH. The protocol would also enable solo validators to borrow efficiently against their otherwise illiquid stake.
Our mechanism achieves a single, fungible LST across all validators without relying on governance, trusted hardware (e.g., SGX), or permissioned operator sets. The protocol leverages EIP-7002 (Execution Layer Triggerable Withdrawals) and EIP-7251 (“MaxEB”) from Pectra. Validators need only point their withdrawal credentials to the protocol.
To counter a potential decrease in the cost of a 51% attack on Ethereum and discourage dominance by single validators, the protocol dynamically limits the achievable leverage using an economic anti-concentration mechanism that disproportionately discourages larger validators. This aims to prevent any single entity from gaining excessive control over Ethereum through the protocol.
Background
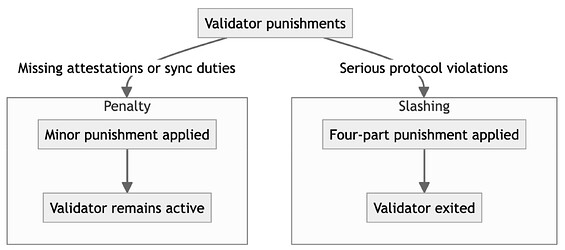
Ethereum’s protocol uses two types of negative incentives for validators: penalties and slashing.
Penalties are applied for missed attestations and sync committee duties. They’re relatively mild—a validator can recover from one day of downtime with about one day of uptime.
Slashing, however, is more severe. It’s applied for serious protocol violations, such as proposing or attesting to multiple blocks for the same slot. This punishment consists of four parts:
-
An initial penalty: Post-Pectra, this would be 1 ETH per 4,096 ETH of effective balance. For a 32-ETH validator, the loss would be 0.00781 ETH.
-
A correlation penalty for mass slashing events: Typically zero, this penalty could potentially wipe out a validator’s entire balance if a third or more of the total stake is slashed within the 18 days before and after the validator’s slashing. In a scenario where 1% of the total stake is slashed, the correlation penalty would be at most 0.960 ETH for a 32-ETH validator.
-
Penalties for missed attestations: Ethereum automatically invalidates all attestations from the slashed validator until they become withdrawable, which occurs after 8,192 epochs. This penalty would amount to 0.0564 ETH for a 32-ETH validator today.
-
An inactivity leak penalty: If the chain is not finalizing, slashed validators incur additional costs. A 32-ETH validator would suffer a loss of 0.0157 ETH for a leak spanning 128 epochs.
If up to 1% of the total stake is slashed and inactivity leaks amount to no more than 128 epochs, slashing a 32-ETH validator would result in a loss of at most approximately 1.04 ETH—just 3.25% of the balance.
This means that, outside of extraordinary mass slashing events, most of the ETH held by a single independent validator is not at risk even if that validator can misbehave arbitrarily.
Prior Work
Several approaches have explored LSTs in this context:
-
Justin Drake proposed an LST mechanism for solo validators that relies on trusted hardware (SGX) to prevent slashing penalties.
-
Dankrad Feist proposed a two-tiered staking system with separate slashable and non-slashable capital tiers.
-
Lido allows ETH holders to “lend” their ETH to node operators without giving those node operators the ability to steal their funds. Their Community Staking Module supports permissionless participation by solo stakers who put down a bond.
-
Rocket Pool enables solo validators to “borrow” up to 24 ETH for each 8 ETH they provide. However, they must also stake RPL tokens—at least 10% of the borrowed amount—and share validator rewards proportionally.
-
frxETH also allows solo anonymous validators to borrow up to 24 ETH for each 8 ETH they provide, but the borrowed ETH can only be used to create new validators.
SOLO, however, offers solo validators unique advantages:
-
It allows them to create validators with as little as 1.25 ETH.
-
It enables minting of a single, fungible LST for any validator without relying on trusted hardware, governance, a permissioned operator set, or staking of an additional token.
-
It compensates LST holders for the time value of their ETH and the risk of bad debt through a market-based funding rate.
-
It requires no changes to Ethereum, except for EIP-7002 and EIP-7251, both in Pectra.
-
It dynamically counterbalances the potential risk it poses to Ethereum of a 51% attack, using a mechanism that disproportionately discourages larger validators from accumulating too much stake.
Protocol Overview
The mechanism draws inspiration from synthetic stablecoin systems like RAI. Node operators act as borrowers, minting an LST called SOLO against validators’ staked ETH, while SOLO holders serve as lenders. If a validator’s SOLO “debt” becomes too high relative to their stake, they’re liquidated and force-withdrawn. A dynamic funding rate compensates SOLO holders for the time value of the underlying ETH and the risk of bad debt, making the token trade close to 1 ETH.
The protocol defines the loan-to-value (LTV) of active validator i, whose withdrawal credentials point to the protocol, as follows:
debt_i is the amount of the SOLO minted against validator i, including any unpaid funding, and collateral_i is validator i's effective balance in Ethereum’s consensus layer.
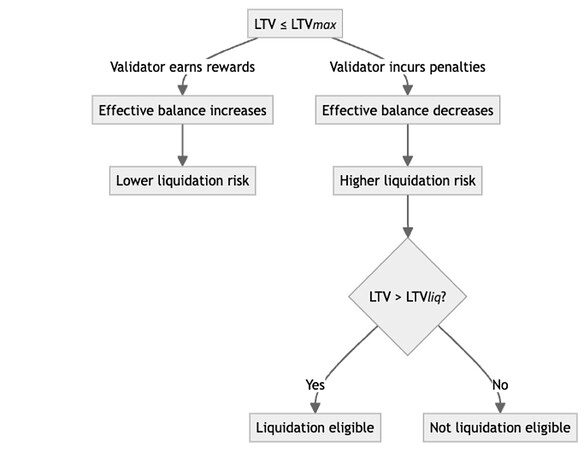
A validator’s LTV can increase due to SOLO minting, funding, penalties, or partial withdrawals, raising their liquidation risk. Conversely, their LTV can decrease due to validator rewards and additional deposits, lowering this risk.
LTV_{max} is the maximum allowed LTV after SOLO minting and partial withdrawals. It is strictly less than 100% and also caps the system’s achievable leverage by limiting how little operators can put forward relative to the validator’s stake size.
LTV_{liq} is the liquidation threshold—the highest LTV before a position becomes eligible for liquidation and forced withdrawal—and must be at least LTV_{max}. Its value should account for potential losses during delays between liquidation eligibility and execution (e.g., if the validator is a proposer and censors the liquidation) and during the exit queue following the forced withdrawal.
H_i is the health factor of validator i, indicating how close it is to liquidation eligibility, if it has any debt:
A value of H_i below 1 makes the validator eligible for liquidation.
Following the analysis in the Appendix, we could estimate values of 96.1% for LTV_{max} and 96.4% for LTV_{liq}.
Minting
To mint SOLO, the withdrawal credentials of the validator must point at a protocol-controlled surrogate contract. Surrogate contracts are used to attribute withdrawals from the consensus layer. If the validator’s withdrawal credentials haven’t been migrated to 0x01 yet, the operator should migrate them and set them to the surrogate contract.
If its withdrawal credentials point at the contract, a validator can be registered by the operator by calling register. The operator can then call mint to mint SOLO against the validator.
The protocol should also offer a method deploy that atomically transfers 32 ETH from the caller, deploys a new validator via Ethereum’s deposit contract, with withdrawal credentials set to the surrogate contract, registers it, and mints SOLO.
Withdrawing
Operators initiate the full withdrawal of the validator by triggering a voluntary exit in the consensus layer or by calling a function withdraw, which triggers the exit of the validator. Partial withdrawals can only be triggered through withdraw, which ensures that the resulting LTV would be less than LTV_{max}. These functionalities, as with liquidation, depend on EIP-7002.
Once the withdrawal completes, the operator calls a method claim to receive the ETH from the stake. If this were a full withdrawal, the operator must have first paid for any outstanding debt against the validator using method repay.
Liquidating
A validator becomes eligible for liquidation when its health factor drops below 1, which occurs when its LTV exceeds the liquidation threshold. Once eligible, anyone can trigger the liquidation process by calling method liquidate on the validator. This call then triggers the withdrawal of the validator.
After the withdrawal completes, the contract auctions the received ETH for SOLO to pay back the validator’s debt. Any excess ETH can be returned to the validator (or kept as a liquidation fee by the protocol). As LTV_{max} accounts for slashing penalties, the received ETH should suffice to cover incurred losses. In the event that this is not enough, SOLO holders would incur the costs from the bad debt.
Slashing
At the end of the slashing process, the protocol receives any remaining stake of the validator after penalties have been applied. The protocol then auctions this ETH for SOLO in order to cover the slashed validator’s debt, following a similar process as a liquidation.
Funding Rates
A mechanism is needed to compensate SOLO holders for the time value of their ETH, as well as for the risk of any bad debt (e.g., from a significant mass slashing event or prolonged inactivity leak). Otherwise, SOLO wouldn’t trade close to 1:1 with ETH, which is essential for the protocol.
We propose using a dynamic, market-based funding rate. SOLO minters (debtors) pay this rate to SOLO holders (lenders). It works by proportionally increasing debts, with SOLO holders benefiting through continuous token rebasing (akin to Lido’s stETH daily rebasing). If the SOLO price falls below 1 ETH, the funding rate rises, making SOLO holding more appealing. If the SOLO price rises above 1 ETH, the funding rate falls, making SOLO holding less attractive. In extreme cases where the SOLO price persistently remains below 1 ETH, the funding rate would eventually rise so high that all positions would be liquidated.
This funding rate can be implemented in various ways. For real-world examples, see the funding rate used in RAI and Squeeth. However, unlike with those mechanisms, the SOLO funding rate can be floored at 0%, avoiding the need for negative rebasing. To prevent the possibility of a sustained depeg in which SOLO trades at higher than 1 ETH even when rates are 0%, the protocol can allow unlimited minting of SOLO against native ETH 1:1 whenever the funding rate is at 0%. Anyone can then redeem SOLO for this ETH at a 1:1 ratio. This reserve of ETH must be emptied before the funding rate can rise above 0% again.
In practice, any increase in protocol returns would likely trigger a surge in SOLO demand, prompting a rise in the funding rate. The reverse holds as well. This self-balancing mechanism becomes even more efficient due to the low entry costs. Nevertheless, SOLO enables solo validators to deploy their borrowed funds into higher-yielding ventures while still operating the validator—a potentially profitable strategy if those returns exceed the funding cost when combined with the validator rewards.
Lowering Capital Requirements
The protocol leverages flash loans to significantly lower the capital requirements for solo validators.
Creating a validator
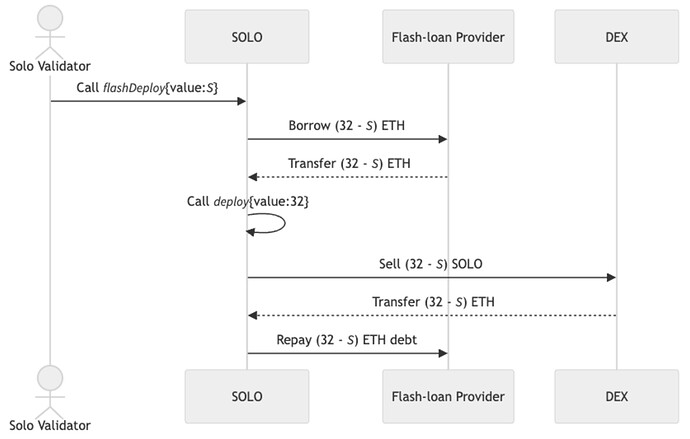
Solo validators would call a special function, flashDeploy, with an amount of ETH, S, as little as 32 (1-LTV_{max}), which does the following:
-
Borrows (32 - S) ETH from a fee-free flash-loan provider to reach 32 ETH with S;
-
Calls
deploywith 32 ETH, along with validator information, to mint (32 - S) of SOLO; -
Exchanges (32 - S) of SOLO for (32 - S) ETH in a decentralized exchange (assuming no price impact);
-
Repays the (32 - S) ETH debt with the flash-loan provider.
Solo validators must then maintain a health factor of at least 1 to avoid liquidation, as this validator would accumulate funding while it’s active.
For an LTV_{max} of 96.1%, the minimum required amount would be approximately 1.25 ETH (i.e., 32 (1 - LTV_{max})), reducing the entry cost for solo validators by a factor of 25.6.
Withdrawing a validator
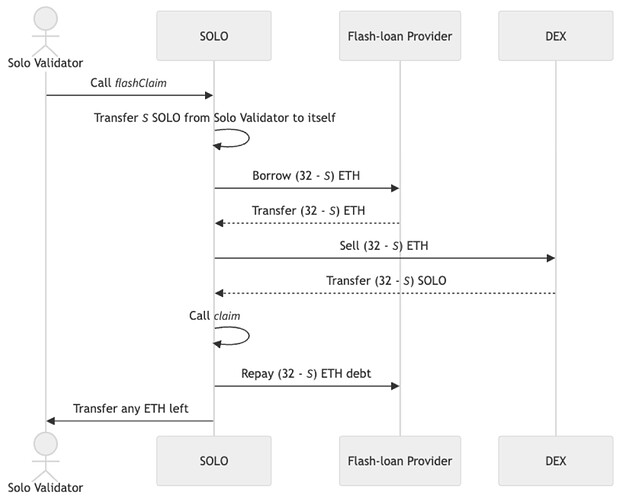
To withdraw the initial amount deposited, S, and rewards, solo validators only need to cover any additional debt accrued, \Delta debt —not the full debt of the validator for (32 - S) SOLO. They’d initiate this process by triggering the full withdrawal of the validator in the consensus layer or through function withdraw. After the withdrawal is completed, they’d call function flashClaim, which does the following:
-
Transfers \Delta debt SOLO from the solo validator to the protocol.
-
Borrows (32 - S) ETH from a fee-free flash-loan provider;
-
Exchanges (32 - S) ETH for (32 - S) SOLO in a decentralized exchange (assuming no price impact);
-
Calls
claimto settle the validator’s debt of (32 - S + \Delta debt) SOLO; -
Repays (32 - S) ETH debt with the flash-loan provider;
-
Returns any ETH left, (S + rewards - penalties), to the solo validator.
If the withdrawn amount is less than the validator’s debt, the protocol incurs bad debt. This scenario, resulting from potential significant validator losses during mass slashing events or prolonged inactivity leaks, would render flashClaim inoperable as there wouldn’t be enough ETH to repay the flash-loan. However, since solo validators only receive the ETH left after debt repayment, their expected return in this scenario would be zero, meaning that no ETH remains locked for them.
Anti-Concentration: Discouraging Large Validators
By reducing the cost of creating a validator, the protocol fosters decentralization and the proliferation of small validators, but it also may reduce the costs of accumulating very large amounts of stake and even potentially executing a successful 51% attack on Ethereum. While the protocol’s benefits are theoretically available to both attackers and honest users, coordinated attackers may be more likely to exploit this advantage effectively.
To counterbalance this risk, we propose an anti-concentration mechanism: a dynamic leverage adjustment that automatically decreases LTV_{max} as the protocol’s share of the total ETH staked grows. One possible formula for this adjustment would be the following:
where LTV_{max}^{t_0} is the initial maximum LTV (e.g., 96.1%).
This mechanism serves two purposes.
First, it helps ensure that SOLO does not dominate Ethereum staking. If SOLO ETH becomes too large a share of all ETH staked, then SOLO will stop providing significant leverage.
But an additional benefit of the mechanism is that it helps ensure that SOLO itself is not dominated by a few large stakers. It does this by disproportionately discouraging large validators from adding more stake.
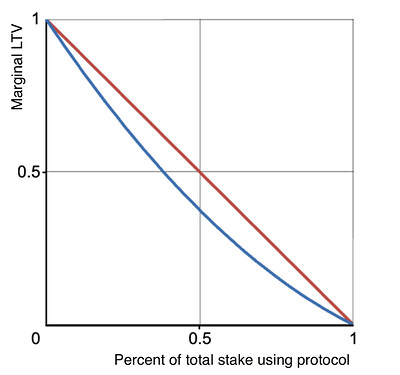
Consider the “marginal LTV ” for an individual validator—the ratio of the amount of SOLO that they can mint for each new unit of ETH they put in as collateral. For anyone who is not yet using the protocol, their marginal LTV is equal to LTV_{max}. But for anyone who is already a staker using the protocol—particularly a large one—the calculus is different. Because of the anti-concentration mechanism, each additional unit of collateral they deposit increases the LTV for all of their stake, requiring them to deposit additional collateral to support all of their existing SOLO debt. This means the marginal LTV for this large validator is actually lower than the marginal LTV of a small validator.
To calculate the marginal LTV, we can start with the formula for the maximum amount of debt that a user, Alice, can take out, debt_{max}, as a function of the amount she has staked through SOLO, C_{Alice}. This is expressed partly in terms of the total amount of ETH that other stakers are staking through SOLO:
The user’s marginal LTV is just the derivative of that formula with respect to the user’s collateral, which works out to:
The upshot of this formula is that users who already have a large amount of collateral being used in the system face a lower marginal LTV than smaller users.
The chart below shows both effects of the anti-concentration mechanism. The red line shows the marginal LTV for a small staker considering using SOLO, as a function of the percent of total stake that is using SOLO. The blue line shows the marginal LTV for a staker who already controls half of the stake in SOLO.
Importantly, this mechanism does not depend on any kind of identity-based Sybil resistance. Attackers can’t avoid it by splitting their holdings across multiple validators or by consolidating large amounts of ETH into single validators. This anti-concentration mechanism provides an economic disincentive for large stakers to accumulate stake through SOLO.
Conclusion
SOLO addresses key challenges faced by solo validators: high entry barriers and limited liquidity for their stake. All in all, we believe this mechanism could make solo validating significantly more attractive.
Appendix
A 32-ETH validator would incur a maximum loss of 0.00867 ETH if offline for an entire exit queue lasting up to 5.6 days as of today. If the validator’s liquidation was delayed by a day, the maximum loss would increase to 0.0102 ETH. Should inactivity leaks occur during this process for up to 128 epochs, the loss would rise to 0.0259 ETH. Moreover, if the validator is slashed during the withdrawability delay period following the exit queue, incurring at most penalties for 1.04 ETH, the total loss would reach 1.07 ETH.
To prevent immediate liquidation when funding accrues, we introduce a buffer between LTV_{max} and LTV_{liq}. This buffer, set at 0.3% of the borrowed amount, would mean that LTV_{liq}=1.003\cdot LTV_{max}.
The maximum loss LTV_{liq} can tolerate without causing bad debt, as a function of LTV_{max} is 32 (1-LTV_{max}). Thus,
Now, potential\,loss=penalties + buffer= 1.07 ETH +\,0.003 \cdot borrowed\, amount. Since borrowed\, amount is 32\cdot LTV_{max} ETH, the buffer is 0.003( 32\cdot LTV_{max}).
Consequently, substituting back into the equation gives the following:
Solving this inequality yields maximum values of \approx 96.1% for LTV_{max} and \approx 96.4% for LTV_{liq}.