The Costs of Censorship: A Modeling and Simulation Approach to Inclusion Lists

[soispoke]

Thomas Thiery - November 10th, 2023

Thanks to Julian, Francesco, Caspar, Barnabé, Anders, Mike and Toni for helpful comments and feedback on the draft.

References	tldr
Fun and games with inclusion lists	Foundational model for economic games (e.g., block stuffing, subsidizing transactions) being played by proposers around ILs
No free lunch – a new inclusion list design	Most recent Vanilla Forward IL proposal
Cumulative, Non-Expiring Inclusion Lists	Cumulative, non-expiring forward IL proposal
Spec’ing out Forward Inclusion-List w/ Dedicated Gas Limits	Specs and implementation of “Forced” ILs (i.e., no block stuffing allowed)

Introduction

Proposer–Builder Separation (PBS), by distinguishing the role of block construction from that of block proposal, shifts the computational complexity of executing complex transaction ordering strategies for Maximum Extractable Value (MEV) extraction to block builders. Block proposers (i.e., validators randomly chosen to propose a block), instead of building blocks locally, can now access blocks from a builder marketplace, via trusted intermediaries known as relays. Relays act as trust facilitators between block proposers and block builders: they validate blocks and verify payments received by block builders, and only forward valid headers to proposers. This ensures proposers cannot steal the content of a block builder’s block.

Since its inception, PBS has gained a lot of traction and almost 95 % of blocks on Ethereum were proposed via MEV-Boost in the past few months. But outsourcing block production to a handful of entities —90.46% of blocks are built by the top five block builders—and depending on trusted third parties—98% of MEV-Boost blocks are proposed by the top five relays— to mediate interactions between builders and proposers introduced challenges and new vectors of centralization. A significant agency cost observed post-PBS introduction is the potential threat to the censorship resistant (CR) properties of the Ethereum network. As builders and relays are often known entities operating under specific jurisdictions, they are obliged to comply with their respective regulatory frameworks. These entities are expected to avoid interacting with a given set of Ethereum transactions (e.g., transactions from or to addresses listed on the OFAC SDN list), leading to additional inclusion delays for censored transactions (i.e., “weak censorship”). Today, according to censorship.pics, 73.86% of the builders and 31.55% of the relays are censoring Ethereum transactions interacting with sanctioned adresses. Only 6.95% of proposers are censoring, and they could go back to local block building but (1) they would lose out on rewards from MEV and priority fees and (2) this would defeat the whole point of PBS in the first place. Over the past few years, ideas have been proposed to improve the CR properties of the network by incentivizing (or forcing) network participants to include transactions flagged as censored by regulated entities. With the advent of increased relay and builder censorship, there has been an influx of research focused on inclusion lists (ILs) and their various designs and implementations over the past few months.

In this post, we provide a modeling approach to CR and inclusion lists, to uncover the games and trade-offs involved in the dynamic interactions between honest and censoring proposers. Utilizing an implementation of the proposed model, we then define key metrics to measure economic and CR attributes under various scenarios.

Empirical Observations

We used Blocknative mempool data from October 12th to 19th, 2023, combined with the OFAC Ethereum addresses dataset to identify and flag transactions interacting with sanctionned addresses. This led to a dataset of 5,899,637 flagged transactions that were seen in the mempool and succesfully landed onchain. The empirical data was utilized to derive key parameters in our model, detailed subsequently.

Game Progression

The game has infinite amounts of rounds. In round N, proposer P^{N} is randomly selected to build a block B^{N}. Note that this doesn’t represent the current block-building process under PBS, in which proposers access blocks from a builder marketplace, and builders compete for the right to build blocks in a MEV-Boost Auction. Thus, this model is not well-suited to capture collusion, side-channels and bribes (e.g., retro-bribes) between builders and proposers. However, we think the model is still useful to illustrate the interesting dynamics at play between Honest Proposers P^H and Censoring Proposers P^C. A censoring proposer choosing not to include any censored transactions in his blocks or ILs can be thought of a censoring proposer that only connects to a censoring builders.

Model Definition

Block Proposers

Let P be the set of all block proposers, and define subsets P^H and P^C of P, representing Honest Proposers and Censoring Proposers, respectively:

P = P^H \cup P^C

Blocks

Let B^N be a block that contains a set of transactions \{T^1, T^2, ..., T^n\} selected from the mempool M in which unconfirmed valid transactions are pending, where n is the total number of transactions in block B^N. The block base fee, B^N_{\text{base_fee}}, is dynamically adjusted by the protocol according to the EIP-1559 update rule. Each transaction uses an amount of gas T^i_{\text{gas_used}}, and transactions can be included in a block until the 30M gas limit, denoted B^N_{\text{gas_limit}}, is reached.

Transactions

Each transaction T^i has the following properties:

• T^i_{hash}: A unique transaction hash.
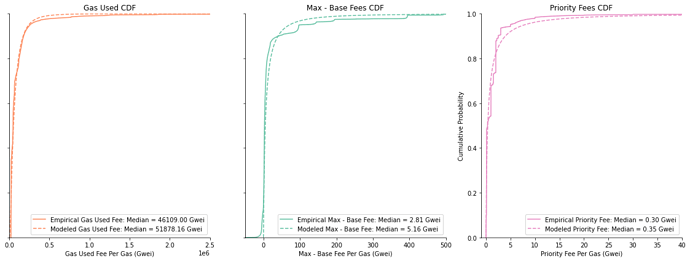
• T^i_{\text{gas_used}}: The gas used by a transaction, drawn from a lognormal distribution \text{Lognormal}(\mu, \sigma), where \mu and \sigma, are derived from an empirical fit to gas_used sourced from mempool data (see Figure 1, left panel). The fit yielded values of \mu \approx 51890 and \sigma \approx 0.93. The decision to model T^i_{\text{gas_used}} with a lognormal distribution was based on the fact that the real-world data were strictly positive and right-skewed. The same decision criteria consistently applied across other variables described subsequently. Furthermore, T^i_{\text{gas_used}} \geq 21,000 and each block B has a gas limit of 30M.
• T^i_{\text{base_fee}}: Transaction base fee, given by the B_{\text{base_fee}} of the block that a transaction was included in (see Blocks section above for more details). B_{\text{base_fee}} is initially set to 5 Gwei, and then fluctuates according the the EIP-1559 update rule.
• T^i_{\text{max_fee}}: A user-specified {\text{max_fee}}, so that T^i_{\text{max_fee}} \geq B^N_{\text{max_fee}} must hold for inclusion in block B. The T^i_{\text{max_fee}} for new transactions reflects the user’s maximum willingness to pay for the transaction, and was drawn from a three-parameter \text{Lognormal}(\mu, \sigma) distribution based on empirical mempool data from the difference between {T}^i_{\text{max_fee}} and {T}^i_{\text{base_fee}} (maxfeepergas-basefeepergas, see Figure 1, middle panel). The distribution had values of \mu \approx 5.16, \sigma \approx 1.59, and was slightly shifted to the left (loc \approx -0.03) to account for the fact that {T}^i_{\text{max_fee}} and {T}^i_{\text{base_fee}} sometimes yielded negative values.
• T^i_{\text{priority_fee}}: The {\text{priority_fee}}, often called tip, is included in transactions as a incentive for proposers to include a transaction in their block. T^i_{\text{priority_fee}} is drawn from a lognormal distribution \text{Lognormal}(\mu, \sigma), where \mu and \sigma, are derived from an empirical fit to maxpriorityfeepergas sourced from mempool data (see Figure 1, right panel), with \mu \approx 0.35 and \sigma \approx 1.88.
• T^i_{\text{MEV}}: Maximal Extractable Value (MEV) corresponds to the excess value that can be extracted by adjusting the execution of users’ transactions. For a given transaction, MEV is also often expressed as a single coinbase transfer in the last transaction of a given block. In our model, T^i_{\text{MEV}} reflects this direct payment, is not tied to T^i_{\text{gas_used}}, and is considered as additional rewards collected by proposers. We used a Dune query to collect empirical data and generate a \text{Lognormal}(\mu, \sigma) distribution for T^i_{\text{MEV}} values, with \mu \approx 15.3 and \sigma \approx 2.04. Note that in practice, MEV can also directly be reflected in T^i_{\text{priority_fee}}: we chose to keep both variables separate for more clarity, but it’s important to keep in mind that both T^i_{\text{MEV}} and T^i_{\text{priority_fee}} * T^i_{\text{gas_used}} will be considered as rewards collected by block proposers P.
• T^i_{censorship\_flag}: A flag indicating whether a transaction is censored or uncensored. We let C be the set of censored transactions so that C = \{T^1_{censored}, T^2_{censored}, ..., T^n_{censored}\} and represents 0.12% of all transactions T based on empirical observations from mempool and OFAC Ethereum addresses datasets. In this model, it’s important to note that we assume C to represent transactions that censoring proposers will not want to interact with in any way, shape or form. Today, in practice, C can be thought of transactions that interacted with adresses listed in OFAC’s sanctions lists. Censoring proposers will not include any T^i_{censored} transactions in their blocks, nor will they construct inclusion lists including T^i_{censored}. Furthermore, a transaction will still be considered T^i_{censored} even if it ends up being included in a block built by an honest proposer eventually, because it is still subject to weak censorship whether it lands onchain or not.

Figure 1. Cumulative Distribution Functions (CDFs) for Ethereum Gas Metrics. Empirical and modeled distributions of three distinct Ethereum gas metrics: Priority Fees (left), Max - Base Fees (middle), and Gas Used (right). Each panel presents a comparison between observed data (solid lines) and data obtained through curve fitting using a log-normal distribution (dashed lines).

Inclusion Lists

Every time a proposer P^N is randomly selected to build a block N, denoted B^N, it can also build an inclusion list IL. An IL is composed of a set of transactions flagged as censored C = \{T^1_{censored}, T^2_{censored}, ..., T^n_{censored}\} from the mempool M, with |IL|<=16 following Terence’s specs. Importantly, according to specifications of the most recent forward IL designs, transactions in the IL^N built by proposer P^N have to be included in block B^{N+1}. In practice, inclusion lists can include any transactions, flagged as censored or uncensored. But given the definition of C in our model, we assume that ILs will only be composed of censored transactions or left empty, because uncensored transactions can just be included in the payload instead.

Strategy Space

Honest proposers

In our model, an Honest Proposer is naive and to build block B^N, it creates a subset of M, M^H_{\text{eligible}} such that T^i is in M^H_{\text{eligible}} if T^{i}_{\text{max_fee}} \geq B^N_{\text{base_fee}}, and IL^{N - 1} \subseteq M^H_{\text{eligible}}. Transactions fulfilling these conditions are then prioritized (i.e., sorted in descending order) based on T^i_{priority\_fee} and included in the block until the 30M B^N_{\text{gas_limit}} is reached.

Policy Description:

π_{P_{H}} = argmax_{B^{N} \subseteq M^H_{\text{eligible}}} \left( \sum_{T^{i} \in B^{N}} T^{i}_{MEV} + (T^{i}_{\text{priority_fee}} \cdot T^{i}_{\text{gas_used}}) \right)

subject to:

\sum_{T^{i} \in B^{N}} T^{i}_{\text{gas_used}} \leq B^N_{\text{gas_limit}}

Given:

M^H_{\text{eligible}} = \{ T \mid T \in (M \cup IL^{N-1}), T_{\text{max_fee}} \geq B^N_{\text{base_fee}} \}

An Honest Proposer also builds an inclusion list IL^N with T^i_{censored} transactions so that |IL| <= MAX_TRANSACTIONS_PER_INCLUSION_LIST.

Censoring proposers

A Censoring Proposer builds block B^N by creating a subset of M, M^C_{\text{eligible}} that contains all transactions from M but excluding censored transactions such that M^C_{\text{eligible}} = C

where:

C = \{{T^1_{censored}, T^2_{censored}, ... T^n_{censored}}\}

and:

IL^{N - 1} \subseteq C

We also assume censoring proposers are profit maximizing parties, and will strategically adapt their policies when they are selected to propose a block.

• If P^{N-1} was a censoring proposer and IL^{N-1} is empty, Censoring Proposer P^{N} constructs a block B^N by following the policy described above, similar to one of an honest proposer, the only differences being P^C choosing from M^C_{\text{eligible}}, and not making IL^{N} for P^{N+1}.

• If IL^{N-1} is not empty, the Censoring Proposer P^C again follows the policy described above, but if the total gas used in the block is less than the 30M, they face a choice:

  • We then introduce the concept of subsidizing transactions to strategically stuff a given block, described in Barnabé’s Fun and Games post. Note that this strategy isn’t currently possible by default, but could be implemented via intent-based mechanisms (e.g., ERC-4337 paymasters), or by charging a block-based base fee at the end of the block, rather than per transaction. We let C_S denote the cost of subsidizing. Add transactions from mempool M not meeting T^i_{\text{max_fee}} \geq B^N_{\text{base_fee}} by subsidizing them, such that T^i_{\text{max_fee}} + C_S = B^N_{base\_fee}. Note that the subsidized transactions will be added to fill the block until the remaining space isn’t sufficient to include any transactions from the list, in addition to the transactions that already meet the T^i_{\text{max_fee}} \geq B_{\text{base_fee}} criteria (see Figure 2). We let T^i_{\text{subsidy}} = B^N_{\text{base_fee}} - T^i_{\text{max_fee}}.

  • If subsidizing these transactions is too costly, and outweighs rewards collected via MEV and priority fees, P^C chooses to go offline, causing a missed slot resulting in no transactions being included in B^N. Let C_S denote the cost of subsidizing transactions, R_{\text{priority_fees}} denote tips collected via priority fees, R_{\text{MEV}} denote MEV rewards from coinbase transfers, and R_{CL} denote Consensus layer rewards. Let R_C include attestation and sync committee rewards, which was ≈ 0.04 ETH for month of October, 2023 based on beaconcha.in data and following the methodology proposed by Rated. A proposer, P^C, will choose to go offline, causing a missed slot resulting in no transactions being included in block B^N, if the following condition is met:

C_S > R_{\text{priority_fees}} + R_{MEV} + R_{CL}

Given that R_{CL} = 0.04ETH, P^C will cause a missed slot if C_S > R_{\text{priority_fees}} + R_{MEV} + 0.04ETH.

Policy Description:

Determine the policy for censoring proposers π_{P^C} such that:
\pi_{P_{C}} = \begin{cases} argmax_{B^{N} \subseteq M} \left(\sum_{T^{i} \in B^{N}} T^{i}_{\text{MEV}} + (T^{i}_{\text{priority_fee}} - T^{i}_{\text{subsidy}}) \cdot T^{i}_{\text{gas_used}}\right) & \text{if } IL^{N - 1} = \emptyset \\ \begin{cases} argmax_{B^{N} \subseteq M \setminus IL^{N - 1}} \left(\sum_{T^{i} \in B^{N}} T^{i}_{\text{MEV}} + (T^{i}_{\text{priority_fee}} - T^{i}_{\text{subsidy}}) \cdot T^{i}_{\text{gas_used}}\right) & \begin{aligned} & \text{if } \sum_{T^{i} \in B^{N}} T^{i}_{\text{gas_used}} \leq B_{\text{gas_limit}} \\ & \text{and } C_{S} > R_{\text{priority_fee}} + R_{\text{MEV}} + R_{\text{CL}} \end{aligned} \\ \emptyset & \text{otherwise} \end{cases} & \text{if } IL^{N - 1} \neq \emptyset \end{cases}

The Censoring Proposer thus decides how to build its block based on the state of IL^{N-1}, comparing R_{\text{MEV}}, R_{\text{priority_fees}} and R_{\text{CL}} rewards to the costs of subsidization C_S, and doesn’t build IL^N.

Rewards, Costs, Profits

In this section, we first give an overview of rewards, costs and profits calculation for honest and censoring proposers.

• Block rewards for a given block B, denoted by R^B_{\text{base_fees}}, is defined as the total sum of the products of the base fees and gas used associated with all transactions included in that block. Note that block rewards, since EIP-1559 was implemented, are burnt and are not received by proposers. They are thus ignored from proposer profits calculations. We let:

  R^B_{\text{base_fees}} = \sum_{i=1}^{n} T^i_{\text{base_fee}} \cdot T^i_{\text{gas_used}}

  where:

  • T^i_{\text{base_fee}}: Base fee of the i^{th} transaction included in block B.
  • T^i_{\text{gas_used}}: Gas used by the i^{th} transaction included in block B.
  • n: Total number of transactions included in block B.

• Priority Fee rewards of a block B, denoted as R^B_{\text{priority_fees}}, sums the product of the priority fee and the gas used for each transaction in a block, and can be calculated as:

  R^B_{\text{priority_fees}} = \sum_{i=1}^{n} T^i_{\text{priority_fee}} \cdot T^i_{\text{gas_used}}

  where:

  • T^i_{\text{priority_fee}}: Proposer rewards from priority fees of the i^{th} transaction included in block B.
  • T^i_{\text{gas_used}}: Gas used by the i^{th} transaction included in block B.
  • n : Total number of transactions included in block B.

• MEV rewards of a block B, denoted as R^B_{\text{MEV}}, coming from extra MEV value paid via coinbase transfers.

• Consensus Layer (CL) rewards of a block B, denoted as R^B_{\text{CL}}, represent the sum of attestation and sync committee rewards associated with block proposal. We used beaconcha.in empirical data from October 12th to 19th, 2023 to estimate the median R^B_{\text{CL}}, and used a value of 0.04 ETH, so that:

  R^B_{\text{CL}} = attestation + sync\ {committee}\ rewards ≈ 0.04\ ETH

• Subsidization Costs of a block B, denoted as C^B_{{Cs}}, represent the expenses borne by a censoring proposer to avoid including censored transactions from an IL. These costs arise when a censoring proposer supplements transactions from the mempool M that do not satisfy T^i_{\text{max_fee}} \geq B_{\text{base_fee}}, ensuring that T^i_{\text{max_fee}} + C_S = B_{\text{base_fee}}. We let T^i_{\text{subsidy}} = B_{\text{base_fee}} - T^i_{\text{max_fee}}, so the subsidization costs can be represented as:

  C^B_{{Cs}} = \sum_{i=1}^{n} T^i_{\text{subsidy}} \cdot T^i_{\text{gas_used}}

• Profits for a given block B, denoted Pr^B, represent the net earnings of a proposer based on their policy, calculated as the total rewards minus the total costs incurred in proposing the block.

  For an Honest Proposer, the profit is primarily influenced by MEV, Priority Fees and Consensus Layer (CL) rewards, and can be denoted as:

  Pr^B_{Honest} = R^B_{\text{MEV}} + R^B_{\text{priority_fees}} + R^B_{\text{CL}}

  For a Censoring Proposer, the calculation of profit also considers the strategic decision to avoid proposing a block, such as block stuffing, subsidizing transactions, or going offline and cause a missed slot. This leads to a different assessment of rewards and costs (see Game Progression and Strategy Space section), but the general idea can be expressed as:

  Pr^B_{Censoring} = R^B_{\text{MEV}} + R^B_{\text{priority_fees}} + R^B_{\text{CL}} - C^B_{{Cs}}

Censorship Resistance Metrics

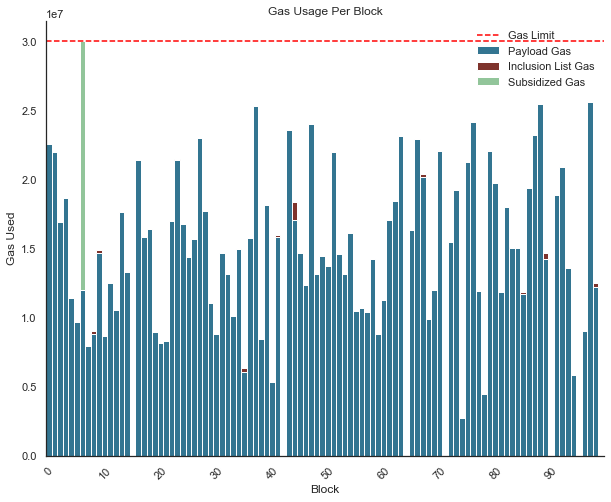
We present visual representations from a singular simulation run spanning 100 blocks, with an honest proposer ratio of 0.7, to offer a clearer interpretation of some model outputs and parameters. Figure 2 represents the sum of gas_used by transactions included across 100 blocks, and indicates from what transactions the gas used originated from (payload, inclusion list, and subsidized transactions). We show that censoring proposers choose between:

• Subsidizing transactions to stuff their block (i.e., green bars represent the gas used by subsidized transactions to reach the gas limit)
• Cause a missed slot (represented by the absence of a bar for a given slot)
  
  

Figure 2. Gas Usage across blocks. This stacked barplot represents the amount of gas_used by transactions included in blocks during a simulation run. The bar colors represent the gas used by payload (blue), inclusion list (red) and subsidized (green) transactions. The horizontal red dashed line represent the 30M gas limit for each block, and the absence of a bar indicates a missed slot caused by a censoring proposer.

Missed Slots

Figure 2 also highlights instances where Censoring Proposers opt to go offline, leading to missed slots, as indicated by blocks where no gas is used (shown by the absence of a bar in the plot). These missed slots occur when Censoring Proposers determine that the expense of subsidizing transactions from mempool M that don’t satisfy the T^i_{\text{max_fee}} \geq B^N_{\text{base_fee}} criterion to fill their blocks up to the 30M gas limit outweighs the benefits from priority fee rewards. By doing so, they prevent censored transactions from IL^{N-1} from being included in block B^N, and miss the CL attestation and sync committee rewards assciated with proposing a block, and estimated around 0.04 ETH per block.

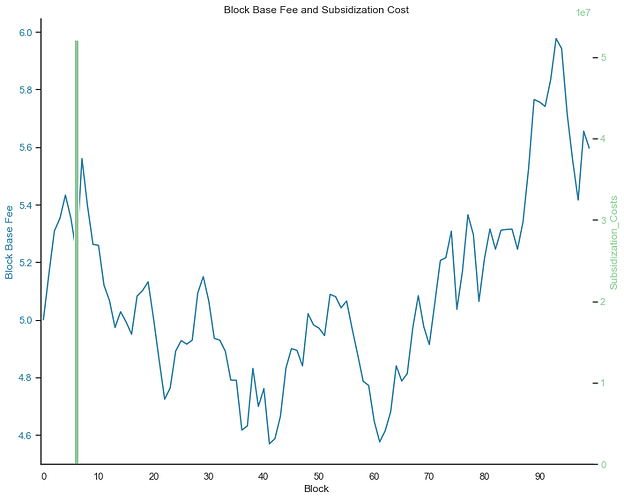
Subsidization Costs

Figure 3 represents B^N_{\text{base_fees}} and subsidization costs C^B_{{Cs}} across 100 blocks. We notice spikes in base fees right after a block was stuffed with subsidized transactions. This is expected, since the EIP-1559 update rule update rule triggers a 12.5% increase in B^N_{\text{base_fee}} for B^{N} if B^{N-1} was full.

Figure 3. Block Base Fee and Subsidization cost. The figure represents the block base fee B^N_{\text{base_fee}} (blue line) in Gwei across 100 blocks, as well as the costs associated with subsidizing transactions (green bars) for censoring proposers looking to stuff their blocks to avoid including censored transactions from an inclusion list. This figure represents a simulation run with 100 blocks, an honest proposer ratio set to 0.7.

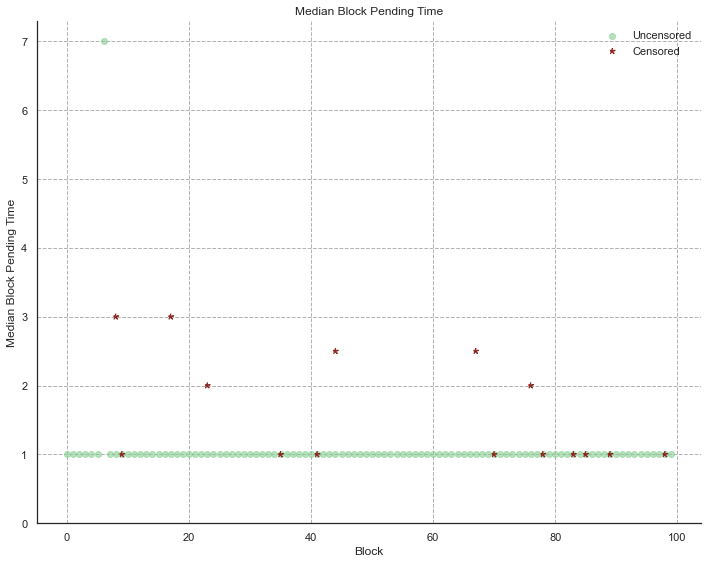
Block Pending Time

Number of blocks between the moment at which a transaction was seen in the mempool M, and the moment at which it was included in a block. Figure 4 shows the median pending time for all censored and uncensored transactions across 100 blocks for a given simulation run, given an honest proposer ratio of 0.7. We observe a longer median block pending time for censored transactions, as censoring proposers will cause missed slots or stuff their blocks in order to avoid having to include them.

Figure 4. Median Block Pending time for censored and uncensored transactions. Scatterplot showing the median block pending time for censored (red stars) and uncensored (green circles) transactions, across 100 blocks for a single simulation run with the honest proposer ratio set to 0.7.

Profits

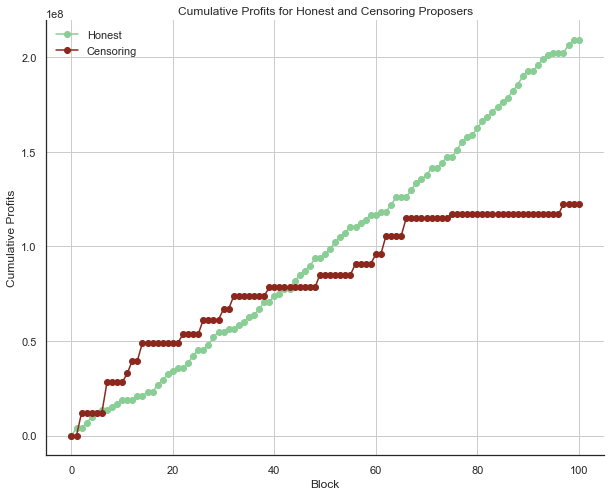
Figure 5 shows the normalized cumulative profits Pr^B_{Honest} and Pr^B_{Censoring} across 100 blocks, given an honest proposer ratio of 0.7.

Figure 5. Cumulative profits for honest (green line) and censoring (red line) proposers, across 100 blocks for a single simulation run with the honest proposer ratio set to 0.7.

Simulations results

Finally, this section presents the outcomes of simulations focusing on essential CR metrics, exploring various scenarios influenced by honest proposer ratios ranging from 0 to 1 (with a step of 0.1). We ran 1000 simulation runs for each honest proposer ratio, each simulation run including 100 blocks, with the percentage of censored transactions set to 0.12%, and a maximum transactions count for ILs set to 16.

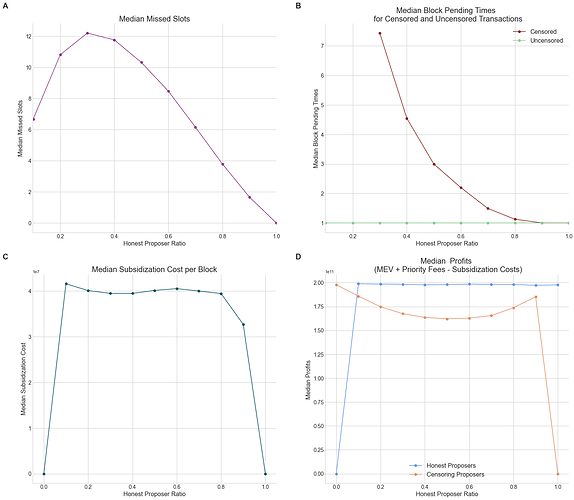
Figure 6 illustrates these outcomes, and reveals:

• An increase in missed slots due to censoring proposers going offline, which coincides with the honest proposers’ ratio climbing from 0 to 0.3 (Figure 6.A). The reason behind this is the higher probability of a censoring proposer, who follows an honest one in proposing a block, deciding to cause a missed slot according to their policy P^H. Conversely, as the proportion of honest proposers continues to grow beyond 0.3 towards 1, a reverse trend emerges. Here, the median number of missed slots begins to decline, attributed to the increasing presence of honest proposers in the network.

• A noticeable reduction in the median block pending time for censored transactions, as depicted in Figure 6.B as the proportion of honest proposers grows from 0 to 1. This delayed inclusion of transactions serves as an important metric to assess weak censorship and the effectiveness of inclusion lists. We also show that uncensored transactions are always included in the next block (median pending time = 1) across all honest proposer ratios.

• Figure 6.C and D display the median subsidization costs and profits per block across various honest proposer ratios, respectively. The figures illustrate that Pr^B_{Honest} remain fairly consistent across different honest proposer ratios. In contrast, profits per block for Pr^B_{Censoring} decrease as the proportion of honest proposers grows from 0 to 0.5, and then increases again from 0.5 to 1. This observed pattern in profits, at their lowest when the honest proposer ratio is 0.5 results from:

  1. The decreased likelihood of consecutive block proposals by censoring proposers, enabling the subsequent proposer to submit a block without facing a choice between subsidization and inducing a missed slot (both options leading to more costs, or reduced profits for the censoring proposer) form 0 to 0.5.
  2. From 0.5 to 1, median profits per block increase. This could be due to the increase probability of having enough transactions to fill up a block and subsidize rather than miss a slot as the proportion of censoring proposers goes down, and might also be driven by a reduced subisidization costs (e.g., for 0.9 honest proposer ratio, see Figure 6.C).

Figure 6. Simulation results across honest proposer ratios. Median missed slots (A), median block pending times for censored (red line) and uncensored (green line) transactions (B), median subsidization cost per block for censoring proposers (C), and median normalized profits per block for honest (blue line) and censoring (orange line) proposers across honest proposer ratios from 0 to 1 (D).

Evaluating network resilience across various censorship levels

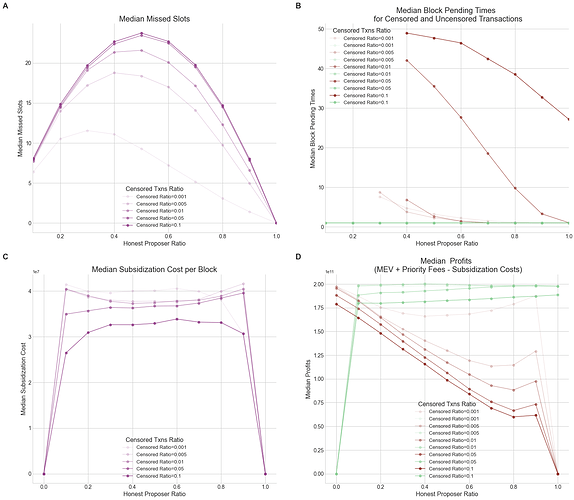
Next, we set out to evaluate how the proportion of censored transactions pending in the mempool affected the aforementioned CR metrics. We simulated different scenarios by varying the percentage of censored transactions with the following values: 0.1%, 0.5%, 1%, 5%, 10%. Figure 7 shows the CR metrics’ response to the escalating proportion of censored transactions in the mempool. We found that an increased proportion of censored transactions caused:

• A larger number of missed slots (Figure 7.A): Notably, the most significant discrepancies were apparent at the lowest ratios (0.001, 0.005, 0.01); however, as the rate of censored transactions grew (0.05, 0.1), m tended to converge, with the exception of the median pending times for censored transactions. These findings suggest that due to the cap on the number of censored transactions per IL, set to 16, there is a threshold beyond which increasing the proportion of censored transactions has no additional impact on the variation of missed slots.
• A increase in median pending time for blocks continues to escalate (Figure 7.B) as the backlog of censored transactions awaiting inclusion grows.
• Lower subsidization costs per block (Figure 7.C) for higher censored transactions ratios.
• A marked decrease in profits for censoring validators when a larger proportion of censored transactions is propagated through the network (Figure 7.D).

These findings highlight the importance of choosing the “right” MAX_TRANSACTIONS_PER_INCLUSION_LISTparameter. An alternative could be setting a MAX_GAS_USED_PER_INCLUSION_LIST, or both, and we think further research could look into an EIP-1559 like mechanism to dynamically adjust the size of ILs based on the number of censored transactions in recent history.

Figure 7. CR metrics across censored transactions ratios. Median missed slots (A), median block pending times for censored (red line) and uncensored (green line) transactions (B), median priority fee rewards normalized per block proposed for honest (blue line) and censoring (orange line) proposers (C), median subsidization cost per block for censoring proposers (D), and median normalized profits per block for honest (blue line) and censoring (orange line) proposers across honest proposer ratios from 0 to 1, and for varios censored transactions ratios (alpha values).

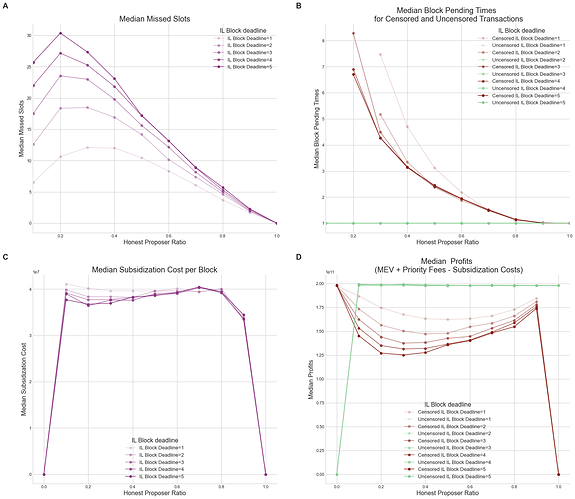
Forward, cumulative IL simulations

To further our understanding of inclusion list (IL) designs, we then applied our simulation framework to the concept of forward cumulative, non-expiring ILs, as discussed in Toni’s recent post. This proposal introduces a block deadline set by proposers for ILs, specifying the duration that censored transactions remain on the IL before being included in a block or until the block deadline expires. Our simulations aimed to map out the effects of different block deadline durations on CR metrics and costs for censoring proposers (see Figure 8). Figure 8.A shows that increasing the IL block deadline forces censoring proposers to cause more missed slots. This is caused by the decreased probability of consecutive censoring proposers, with proposer N not filling the IL for proposer N+1, allowing the latter to propose a block without having to stuff the block or cause a missed slot. We also show that the median block pending times did not significantly differ across various block deadline durations and honest proposer ratios, except for a slight increase in pending times with short deadlines set to 1 or 2 blocks (Figure 8.B). This suggests that extending the block deadline beyond 3 does not substantially enhance the network’s capacity to counteract weak censorship effects. Lastly, the simulations show a reduction in the median profits for censoring proposers as the block deadline increases (Figure 8.E), with this decline primarily driven by the increased frequency of missed slots (Figure 8.A), which leads to a reduction in priority fee rewards (Figure 8.C). Conversely, the subsidization costs per block remained relatively unaffected by changes in block deadline values (Figure 8.D).

Figure 8. CR metrics across IL block deadline values. Median missed slots (A), median block pending times for censored (red line) and uncensored (green line) transactions (B), median priority fee rewards normalized per block proposed for honest (blue line) and censoring (orange line) proposers (C), median subsidization cost per block for censoring proposers (D), and median normalized profits per block for honest (blue line) and censoring (orange line) proposers across honest proposer ratios from 0 to 1, and for varios censored transactions ratios (alpha values).

Future research and considerations

We hope the proposed model can serve as a tool for subsequent research to assess IL designs and their associated trade-offs. Future work could focus on:

• Refining the model, to account for interactions between builders, relays and proposers to reflect the current PBS implementation. The model could also be fine-tuned to model the demand for block space more accurately, evaluate out-of-protocol censorship resistance implementations, or further explore designs in which * active * honest proposers can also choose to subsidize transactions to maximize profits.
• More simulations to analyze the economic and CR attributes of recent implementation suggestions, including a comparison between vanilla forward ILs and forced ILs.
• Testing ideas for different implementation parameters (e.g., inclusion list size) and network conditions. The goal is to push CR R&D towards backtesting against historical empirical data, facilitating a more tangible assessment of IL designs under real-world network conditions and moving towards EIPs.
• Investigating various mechanisms for enabling builders to subsidize transactions presents a particularly intriguing avenue of research.

[The-CTra1n]

Whether or not a transaction included in an IL is already applied to the state machine will be an important philosophical, and probably legal, debate. For the sake of this simulation though, it makes sense that you made the following assumption in that regard:

@soispoke

In this model, it’s important to note that we assume C CC to represent transactions that censoring proposers will not want to interact with in any way, shape or form.

It is probably outside the scope of this work, but wouldn’t there be strategies to place low value/high gas cost transactions into an IL to lower the value of the proceeding block? This probably brings up the question (which I cannot see answered here or elsewhere) regarding who pays for the IL? Is it independent of the 30M gas limit? This seems like a potential vulnerability of ILs, so wondering if you’ve seen it discussed somewhere?

[soispoke]

@The-CTra1n

Whether or not a transaction included in an IL is already applied to the state machine will be an important philosophical, and probably legal, debate. For the sake of this simulation though, it makes sense that you made the following assumption in that regard:

I agree the assumption about how proposers interact with transactions they want to censor doesn’t always hold.

In the most recent forward IL proposal, users pay for the IL, by making sure the maxFeePerGas is at least 12.5% (the max amount the base fee can increase from block to block) higher than the current block base fee.

As for the independence from the 30M gas limit, it’s still up for discussion but feels like an implementation detail, to the more important question is Vanilla (block stuffing works as a way to avoid including ILs) vs Forced ILs (Proposer N+1 has to include transactions from the IL no matter what), this was discussed a bit in this post).